独立基礎を設計するための計算のウォークスルー (ACI 318-14)
基礎は、柱と壁の力を支持土に伝達する重要な建築システムです. エンジニアは、土壌の特性と建物の荷重に基づいて、浅い基礎システムまたは深い基礎システムを選択する場合があります。.
SkyCiv Foundation設計モジュール 米国規格 ACI318-14 に準拠した分離フーチングの解析と設計が含まれます。.
SkyCivのFoundationDesignソフトウェアを試してみたい? 当社のツールを使用すると、ダウンロードやインストールを行わずに基礎設計の計算を実行できます。!
独立基礎を設計するためのステップバイステップ ガイド
寸法要件
独立基礎の寸法を決定するには, サービスまたはファクタリングされていない負荷, 死んだなど (D), 住む (L), 風 (W), 地震 (E), などは、荷重の組み合わせを使用して適用されます, ACIで定義されているとおり 318-14. どちらの荷重の組み合わせが支配するかは、設計荷重と見なされます, 式に示すように、許容土圧と比較されます 1, で推奨されているように セクション 13.2.6 ACIの 318-14.
\(\テキスト{q}_{\テキスト{a}} = frac{\テキスト{P}_{\テキスト{ん}}}{\テキスト{あ}} \右矢印 \) 方程式 1
qa = 許容土圧
Pん = 因数分解されていない設計負荷
A =基礎エリア
フーチングの寸法は、基礎面積を解決することで最初に推定できます。 (あ) 式を使用する 1.
\(\テキスト{あ} = frac{\テキスト{P}_{\テキスト{ん}}}{\テキスト{q}_{\テキスト{a}}} \右矢印 \) 式1a
一方向せん断
一方向せん断限界状態, ビームシアとも呼ばれる, フーチングは、離れた位置にある臨界せん断面に沿った幅広の梁と同様のせん断で破壊される可能性があることを認識しています “d” 柱の正面から (図 1),
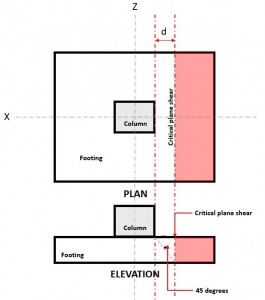
図 1. 一方向せん断の臨界面せん断
の 一方通行 剪断 要求する または V あなた 基礎が図の赤い領域で示されている柱から片持ち梁で離れていると仮定して計算されます。 1, 以下 セクション 8.5.3.1.1.
の 一方向せん断耐力 または ϕVc 極限せん断強度として定義され、式を使用して計算されます。 2 あたり セクション 22.5.5.1.
\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 2 \平方根{\テキスト{f ’}_{\テキスト{c}}} \倍 text{b}_{\テキスト{w}} \倍 text{d} \右矢印 \) 方程式 2 ( セクション 22.5.5.1, インペリアル)
または
\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 0.17 \平方根{\テキスト{f ’}_{\テキスト{c}}} \倍 text{b}_{\テキスト{w}} \倍 text{d} \右矢印 \) 方程式 2 (セクション 22.5.5.1, メトリック)
ϕ剪断 = せん断設計係数
f’c = 規定のコンクリート強度, (psi, MPa)
bw = 基礎の幅, (に, んん)
d = 極度圧縮繊維から縦張力補強材の重心までの距離, (に, んん)
ACIの設計要件を満たすには、せん断需要とせん断容量が次の式を満たす必要があります。 318-14:
\(\テキスト{V }_{\テキスト{あなた}} \leq phi text{V }_{\テキスト{c}} \右矢印 \) 方程式 3 (ACIEq。. 7.5.1.1(b))
SkyCiv 財団設計モジュール, 方程式に従って 3, 一方向せん断利用率を計算します (方程式 4) せん断耐力よりもせん断需要をとることによって.
\( \テキスト{利用率} = frac{\テキスト{せん断需要}}{\テキスト{せん断耐力}} \右矢印 \) 方程式 4
双方向せん断
双方向せん断限界状態, パンチングシャーとも呼ばれます, クリティカルセクションを遠くまで拡張します “d / 2” 柱の面から、そして柱の周囲から (図 2).
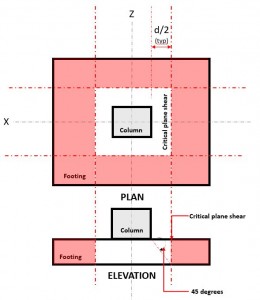
図 2. 双方向せん断の臨界せん断面
の ふたつのやり方需要を聞く または V あなた 臨界せん断面で発生します, の距離に位置する “d / 2” どこ (赤) ハッチングエリア, 図に示されている 2, 以下 セクション 22.6.4.
の せん断耐力 または ϕVc 方程式を使用して計算された最小値によって支配されます 5, 6, そして 7 あたり セクション 22.6.5.2
\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 4 \倍ラムダ倍平方根{\テキスト{f ’}_{\テキスト{c}}} \右矢印 \) 方程式 5 (セクション 22.6.5.2(a) インペリアル)
\(\ファイテキスト{V }_{\テキスト{c}} = left ( 2 + \フラク{4}{\ベータ } \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 6 (セクション 22.6.5.2(b) インペリアル)
\(\ファイテキスト{V }_{\テキスト{c}} = left ( 2 + \フラク{\アルファ_{s} \倍d }{b{の}} \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 7 (セクション 22.6.5.2(c) インペリアル)
または
\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 0.33 \倍ラムダ倍平方根{\テキスト{f ’}_{\テキスト{c}}} \右矢印 \) 方程式 5 (セクション 22.6.5.2(a) メトリック)
\(\ファイテキスト{V }_{\テキスト{c}} = 0.17 \倍左 ( 1 + \フラク{2}{\ベータ } \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 6 (セクション 22.6.5.2(b) メトリック)
\(\ファイテキスト{V }_{\テキスト{c}} = 0.0083 \倍左 ( 2 + \フラク{\アルファ_{s} \倍d }{b{の}} \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 7 (セクション 22.6.5.2(c) メトリック)
注意: β は柱の長辺と短辺の比です。, 集中負荷, または反応面積とαs によって与えられます 22.6.5.3
λ = 同じ圧縮強度の通常のコンクリートと比較した軽量コンクリートの機械的特性の低下を反映する修正係数
f’c = 指定されたコンクリート圧縮強度 (psi, MPa)
d = 極度圧縮繊維から縦張力補強材の重心までの距離, (に, んん)
ACIの設計要件を満たすには、せん断需要とせん断容量が次の式を満たす必要があります。 318-14:
\(\テキスト{V }_{\テキスト{あなた}} \leq phi text{V }_{\テキスト{c}} \右矢印 \) 方程式 8 (セクション 7.5.1.1(b))
SkyCiv 財団設計モジュール, 方程式に従って 8, 双方向せん断ユーティリティ比を計算します (方程式 9) せん断耐力よりもせん断需要をとることによって.
\( \テキスト{利用率} = frac{\テキスト{せん断需要}}{\テキスト{せん断耐力}} \右矢印 \) 方程式 9
たわみ
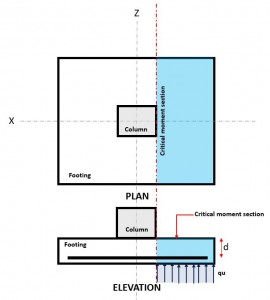
図 3. クリティカルフレクシャセクション
の 曲げ 限界状態が発生するのは クリティカルフレクシャセクション, 基礎の上の柱の面にあります (図 3).
の 曲げ需要 または Mあなた クリティカルフレクシャセクションにあります (青いハッチエリア) 図に示されている 3, 方程式を使用して計算されます 10.
\( \テキスト{M}_{あなた} = text{q}_{あなた} \倍左 ( \フラク{l_{バツ}}{2} – \フラク{c_{バツ}}{2} \正しい ) \倍l_{と} \倍左 ( \フラク{\フラク{l_{バツ}}{2} – \フラク{c_{バツ}}{2} }{2} \正しい ) \右矢印 \) 方程式 10
qあなた =因数分解された土壌圧力, (ksf, kPa)
lバツ = x軸に沿った基礎寸法 (に, んん)
lと = z軸に沿った基礎寸法 (に, んん)
cバツ = x軸に沿った列の寸法 (に, んん)
の 曲げ能力 または ϕMん 式を使用して計算されます 11.
\( \ファイテキスト{M}_{ん} = phi_{\テキスト{たわみ}} \倍A_{s} \倍f_{そして} \倍左( d – \フラク{a}{2} \正しい) \右矢印 \) 方程式 11
ϕ =曲げ設計係数
lバツ = x軸に平行な基礎寸法 (に , んん)
lと = z軸に平行な基礎寸法 (に , んん)
d =極端な圧縮繊維から縦方向の張力補強の重心までの距離 (に , んん)
あs =補強エリア (に2 , んん2)
a =同等の長方形応力ブロックの深さ (に , んん)
fy =補強強度, (KSI, MPa)
ACIの設計要件を満たすには、モーメント需要とモーメント容量が次の式を満たす必要があります。 318-14:
\(\テキスト{M}_{\テキスト{あなた}} \leq phi text{M}_{\テキスト{ん}} \右矢印 \) 方程式 12 (セクション 7.5.1.1(b))
SkyCiv 財団設計モジュール, 方程式に従って 12, 曲げ利用率を計算します (方程式 13) 曲げ能力よりも曲げ需要を取ることによって.
\( \テキスト{利用率} = frac{\テキスト{たわみ需要}}{\テキスト{たわみ容量}} \右矢印 \) 方程式 13
追加の検証
コードに記載されていないその他の検証, 土圧チェックも含めて, 隆起, その他の安定性チェックも検証されています.
土圧
基礎圧力または土壌とフーチングの間の相互作用の決定は、主にフーチングの寸法と、その結果生じる適用荷重の偏心によって決まります。. この結果生じる偏心の位置に応じて, ベース圧力はフーチングに完全または部分的な圧縮を引き起こす可能性があります. この評価により、基礎地盤がフーチングから伝わる荷重全体に耐えられるかどうかを確認できます。.
土圧を手動で計算するための詳細なガイドについては、, このリンクを参照してください: 長方形のコンクリートフーチングの下の圧力分布
最大土圧を比較して利用率を評価します (保守性の状態) 許容総耐力土容量:
\( \テキスト{利用率} = frac{\テキスト{マックス. 土圧}}{\テキスト{総許容地耐力}} \右矢印 \) 方程式 14
隆起
フーチングに作用する支配アキシアル荷重を確認します. ユーザー荷重とコラムの自重を含むすべての垂直荷重を合計します。, 基礎スラブ, 土, そして浮力. コラムに上向きの力が加わった場合, 指定された自重は上向きの力と釣り合う必要があります; さもないと, 設計は不安定性により失敗するリスクがあります.
転覆
フーチングの転倒は、フーチングに作用するすべての力を含むフーチングの点に関するすべてのモーメントを合計することによってチェックされます。. 支配的な転倒モーメントをチェックするには、すべての保守性荷重の組み合わせを考慮する必要があります. 通常, の安全率 1.5-2 フーチングが転倒チェックに合格するかどうかを評価するために使用されます.
スライディング
滑りを確認するには, 右向きの水平抵抗荷重の合計を左向きの荷重の合計で割ります。.
- 転倒モーメント計算例:
- フーチング基礎と下部工土との摩擦による水平力
- パッシブ土壌圧力 (含まれている場合)
- 滑り荷重:
- 有効土圧の水平成分
- サーチャージ合成圧力の水平成分
一般的に, 最小安全率 1.5 使用されている. 基礎に水平力が作用していない場合, 滑りチェックは不要です.
SkyCiv 財団設計モジュール
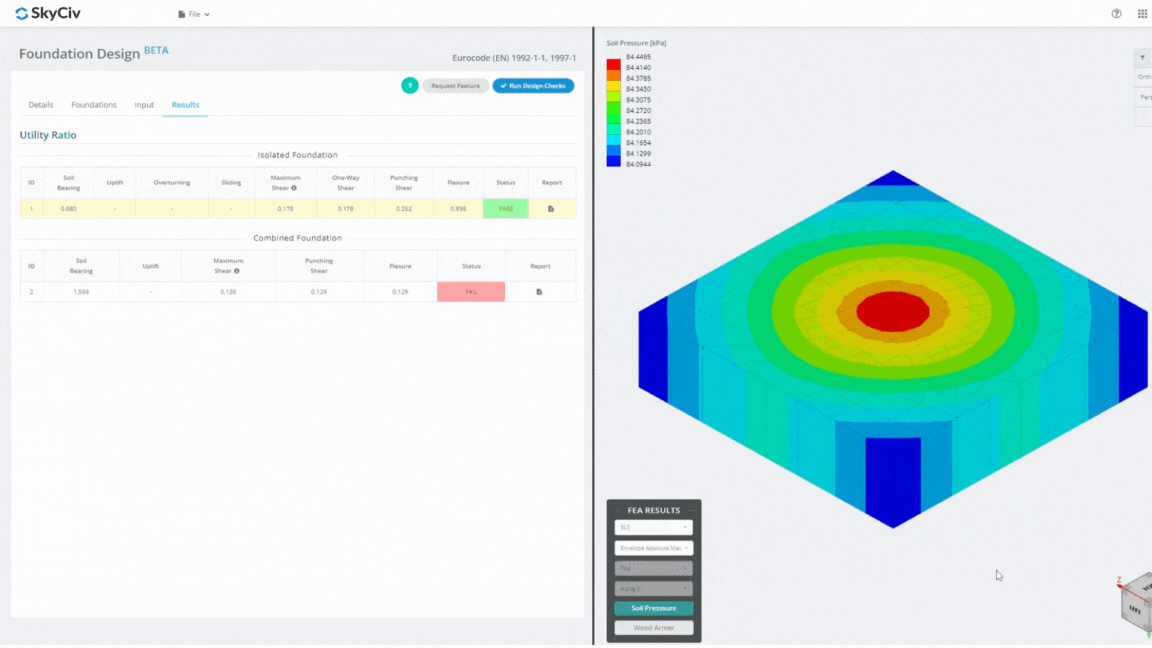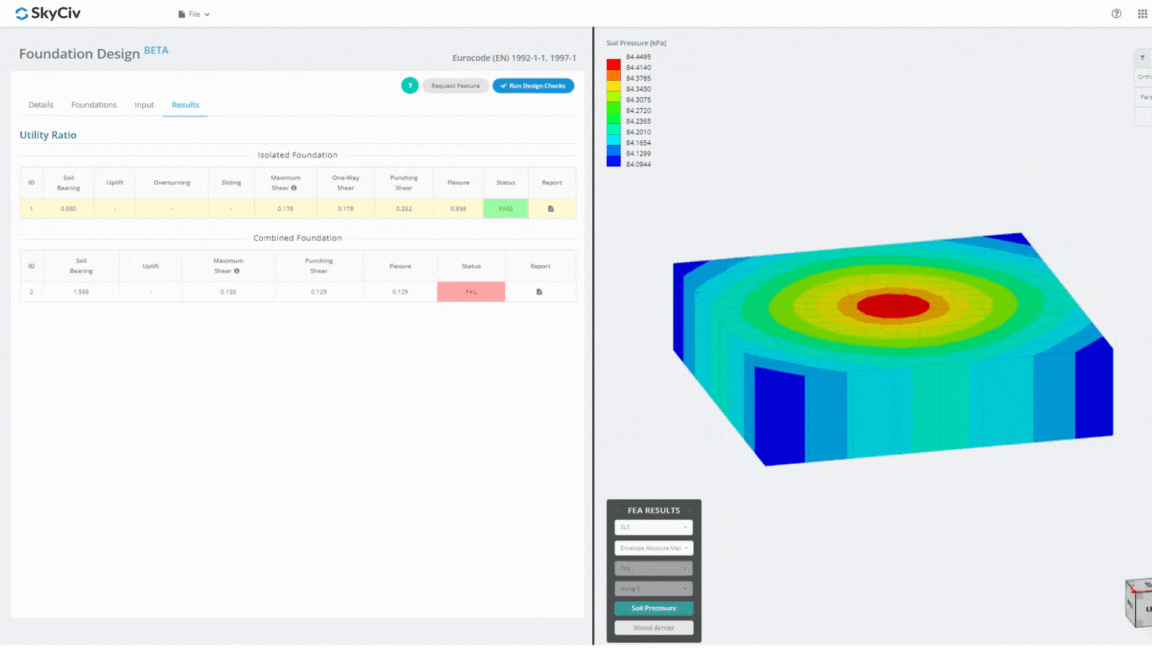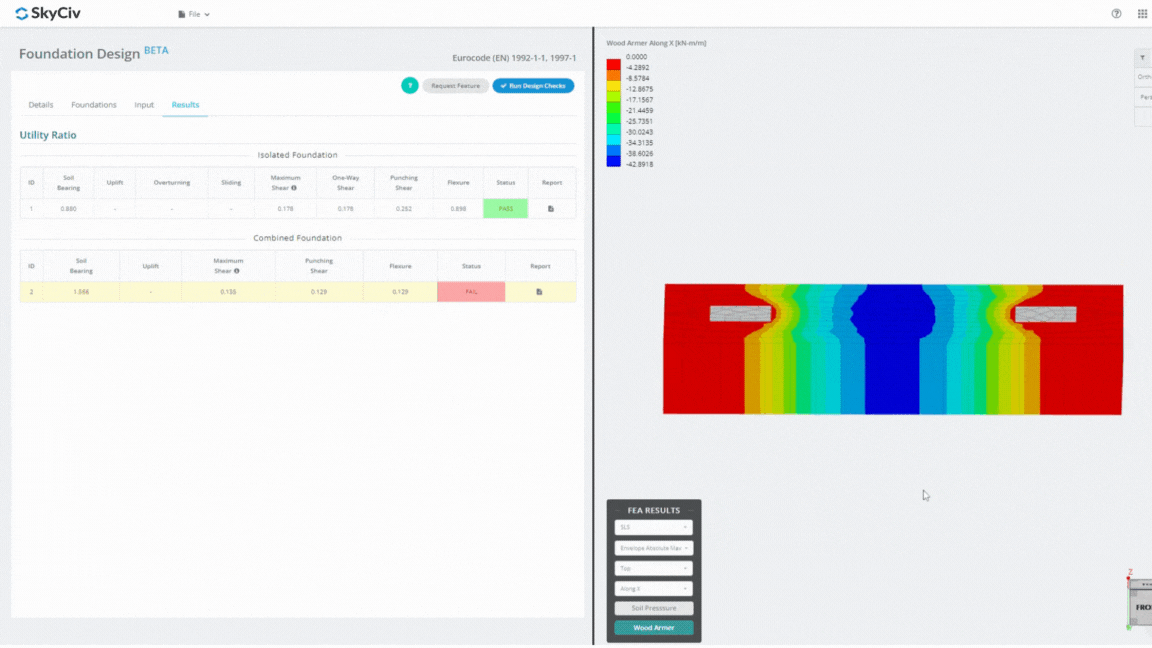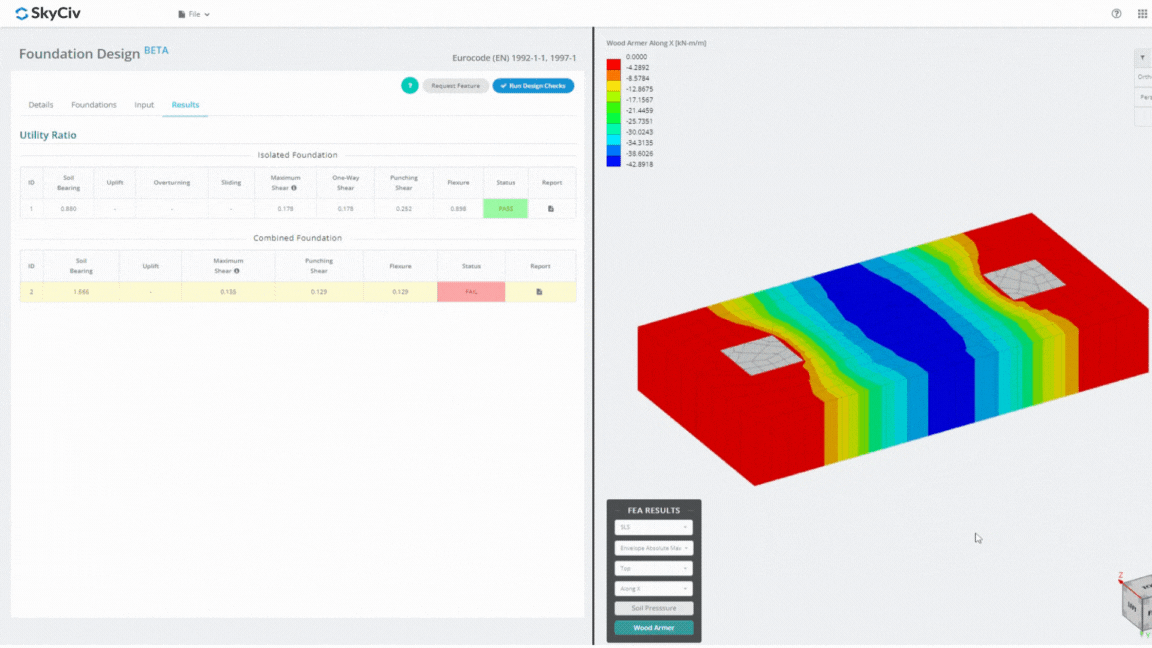
Foundation Design Module は、有限要素解析と統合された強力なツールです。 (醜い), 徹底的な土圧分析と木材アーマー分析を実施して、詳細な曲げチェックを行うことができます. ACI によって指定されたすべての構造チェックを実行します。 318 および上記のその他の検証を行い、それらを包括的なレポートにまとめます。.
SkyCiv財団を始めましょう 今日!
を起動します。 基礎デザイン そして今日試してみてください! 始めるのは簡単ですが、さらにサポートが必要な場合は, その後、必ず私たちを訪問してください ドキュメンテーション または私たちにご連絡ください!
SkyCivユーザーではありません? サインアップして 自由 14 デイトライアル 始めるために!
製品開発者
BSc (民事), 修士課程 (民事)
アルバートパモナグ
構造エンジニア, 製品開発
自分. 土木工学
参考文献
- 構造コンクリートの建築基準要件 (ACI 318-14) 構造コンクリートの建築基準要件に関する解説 (ACI 318R-14). アメリカコンクリート学会, 2014.
- マコーマック, ジャックC。, とラッセルH. 褐色. 鉄筋コンクリートACIの設計 318-11 コード版. ワイリー, 2014.
- テイラー, アンドリュー, et al. 鉄筋コンクリート設計ハンドブック: ACI-318-14のコンパニオン. アメリカコンクリート学会, 2015.




