基礎は、構造の総荷重を地面に伝達および分散することにより、全体的な安定性を提供する構造の不可欠な要素です。. 浅い土台, 長方形または正方形の独立基礎など, 深基礎と比較して構造が簡単で全体的なコストが高いため、好ましいタイプの基礎です。. ベース圧力の推定はフーチングの設計とサイズに大きく影響します。. 通常, 土壌の許容支持力とフーチング下の支配基礎圧力との間の利用率がフーチングの初期サイズの基礎となります。. 基礎の初期寸法が設定されたら, 安全性と安定性のためのさらなる設計チェック, 一方向および二方向せん断など, 曲げ能力, および展開長チェック, 使用されているデザインコードに応じてチェックされます.
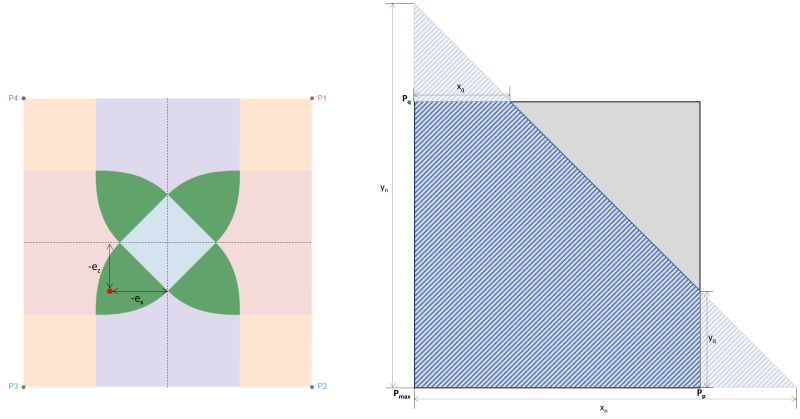
フーチングを二軸曲げする場合 (Mバツ, Mと), アキシアル荷重がかかると仮定します。 (P) 偏心座標に作用しています (eバツ, eと) 中心から回転する傾向がある場合. 土壌とフーチング間の相互作用は、主にフーチングの寸法と、その結果として加えられる荷重の偏心によって決まります。. 結果として生じる偏心の位置に応じて, ベース圧力により、フーチングが完全または部分的に圧縮されます. 実際には, 完全に圧縮されたフーチングを設計することをお勧めします. 部分的な圧縮や土壌と基礎間の接触の喪失を無視してはなりません, しかし、計算が複雑なため、ほとんどの設計者はこのシナリオを避けます。. 結果として生じる偏心がカーン内またはゾーン C の下にある場合、足場は完全に圧縮されています。. ゾーン C の外側の偏心により、基礎が部分的に圧縮されます. 図 1 長方形のフーチング上のさまざまな指定ゾーンを示しています.
この記事では、Bellos に基づいたさまざまなゾーン分類でのコーナープレッシャーの計算に焦点を当てます。 & 痕跡 (2017) とSS. レイズ (1995) 研究.
直角フーチングのゾーン分類
長方形フーチングのゾーン分類は、予想される荷重条件下での土圧分布を推定するための実用的なアプローチを開発するために、さまざまな著者による複数の研究から導かれています。. 図に示すように 1, 5つの異なる地域があります (ゾーン A ~ E) 結果として生じる偏心の位置に応じて. 各ゾーンは異なる負荷に対応します, ベース圧力分布, そして変形. ゾーンC, カーンとも呼ばれる, メインコアです. 基礎を設計するのに理想的な領域です, その結果、基礎が完全に圧縮されます. この領域の次元は 1/6 それぞれの基礎の長さ.
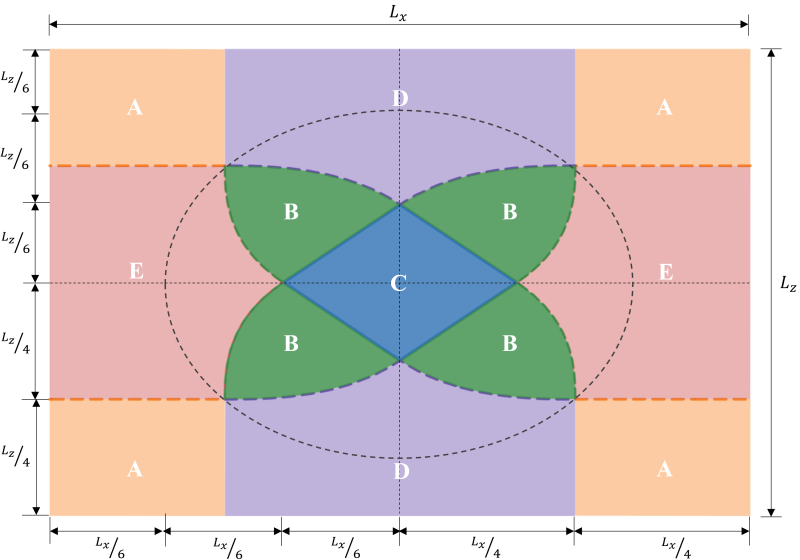
図 1: 直角フーチングのゾーン分類
二次コアは楕円形の領域です (図の破線で囲まれた 1) 長半軸と短半軸が等しい 1/3 それぞれの基礎の長さ. このリージョンは、ゾーン B 全体をカバーします。 & CおよびゾーンDの一部 & E. 二次コアにより、基礎が部分的に圧縮されます. 許容できるフーチング設計のために、セカンダリ ゾーン内の離心率を維持することをお勧めします。.
二次ゾーンを超える偏心は、高い二軸負荷の結果です. ゾーン A 全体とゾーン D の残りの部分をカバーします。 & E. 転倒の危険性があるため、これらの領域でのフーチングの設計は避けることをお勧めします。. したがって, この荷重タイプに合わせてフーチングの寸法を再設計することをお勧めします。.
以下に、各ゾーン分類におけるコーナー圧力を解くための解析式を列挙します。.
ゾーンC (メインコア, 完全な圧縮ゾーン)
述べたように, これはフーチングのベース全体を圧縮状態に設定できるため、フーチングの設計に最も好ましいケースです。, 図に示すように 2. このケースは、カーン内の偏心が小さいか、偏心がないことによって表されます。. 図 2 コーナー P3 での最大圧力によるカーン内の偏心を示します。 & P4 とコーナーの最小圧力 P1 & P2.
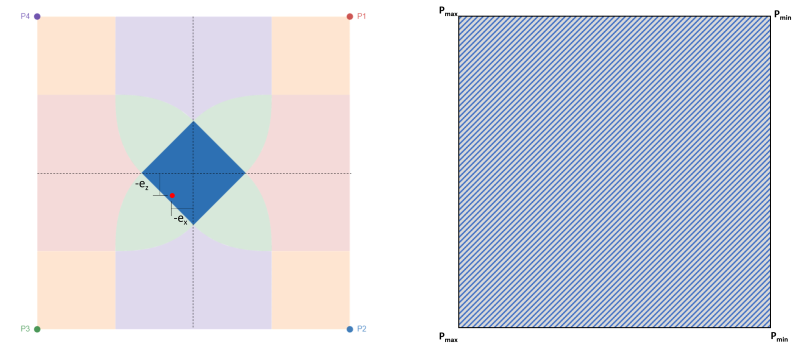
図 2: 偏心 (-eバツ, -eと) ゾーンCにて & 完全な圧縮領域
最大 & 最小コーナープレッシャー (美しい & 痕跡, 2017):
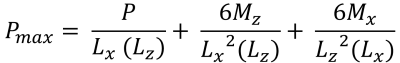
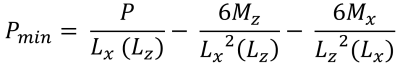
| 偏心によるコーナー圧力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| +eバツ, +eと | P最高 | P最高 | P分 | P分 |
| +eバツ, -eと | P最高 | P最高 | P分 | P分 |
| -eバツ, -eと | P分 | P分 | P最高 | P最高 |
| -eバツ, +eと | P分 | P分 | P最高 | P最高 |
ゾーンA (三角形の圧縮ゾーン)
このケースは基礎の隅々にある 4 つの長方形の領域に対応します。. 通常、二軸偏心が大きい場合に発生します。, コーナーの 1 つに高い三角形の圧縮領域を設ける, 図の斜線部分に示すように 3. 残りの角は土との接触を失います. したがって, このケースは設計上お勧めできません.
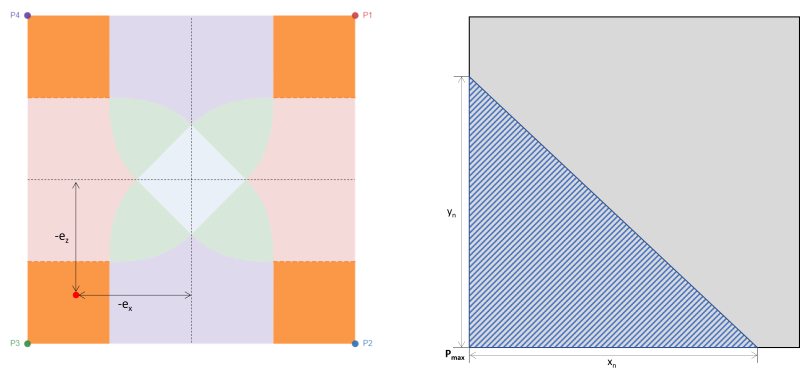 図 3: 偏心 (-eバツ, -eと) ゾーンAで & P3 周囲の三角形の圧縮領域
図 3: 偏心 (-eバツ, -eと) ゾーンAで & P3 周囲の三角形の圧縮領域
最大圧力 (美しい & 痕跡, 2017):
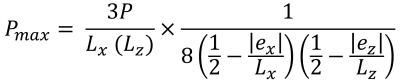
| 偏心によるコーナー圧力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| eバツ(+), eと(+) | P最高 | 0 | 0 | 0 |
| eバツ(+), eと(-) | 0 | P最高 | 0 | 0 |
| eバツ(-), eと(-) | 0 | 0 | P最高 | 0 |
| eバツ(-), eと(+) | 0 | 0 | 0 | P最高 |
ゾーンD (台形圧縮ゾーン)
ゾーン D はフーチングの X 方向に取り付けられた領域の大きな偏心にも対応します。, 図に示すように 4. z方向の偏心 (eと) x 方向よりもはるかに大きい (eバツ). この場合, フーチングの 2 つの角が土壌との接触を失い、台形の圧縮領域が生成されます。. ゾーンAとの比較, これは完全にセカンダリ ゾーンの外側にあります, ゾーン D の一部は依然としてセカンダリ ゾーンによってカバーされています.
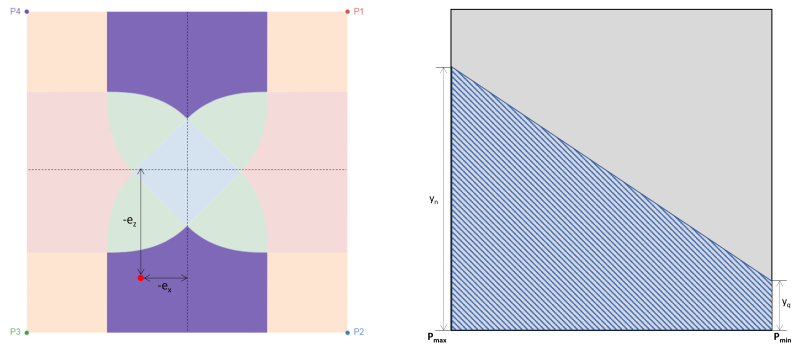
図 4: 偏心 (-eバツ, -eと) ゾーンDにて & P3 周囲の台形圧縮領域
最大 & 最小コーナープレッシャー (美しい & 痕跡, 2017):
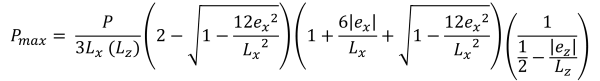
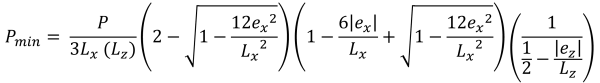
台形圧縮領域の垂直高さ (美しい & 痕跡, 2017):
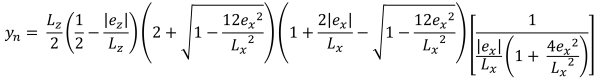
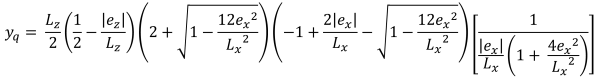
| 偏心によるコーナー圧力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| eバツ(+), eと(+) | P最高 | 0 | 0 | P分 |
| eバツ(+), eと(-) | 0 | P最高 | P分 | 0 |
| eバツ(-), eと(-) | 0 | P分 | P最高 | 0 |
| eバツ(-), eと(+) | P分 | 0 | 0 | P最高 |
ゾーンE (台形圧縮ゾーン)
ゾーンDに似ている, この場合も台形の圧縮領域が生成されますが、これは x 方向の大きな偏心によって引き起こされます。(eバツ).
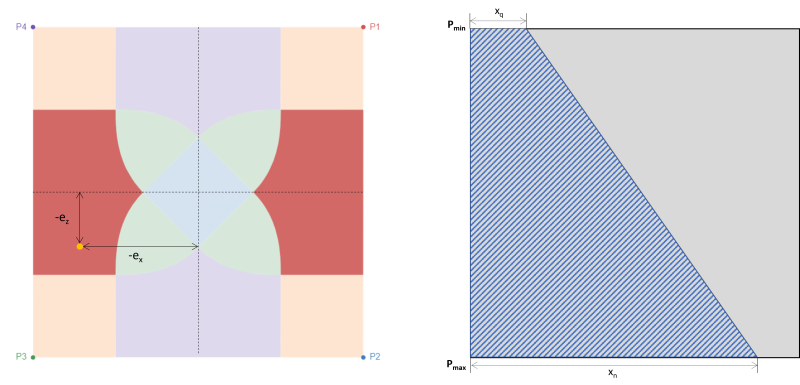 図 5: 偏心 (-eバツ, -eと) ゾーンEにて & P3 周囲の台形圧縮領域
図 5: 偏心 (-eバツ, -eと) ゾーンEにて & P3 周囲の台形圧縮領域
最大 & 最小コーナープレッシャー (美しい & 痕跡, 2017):
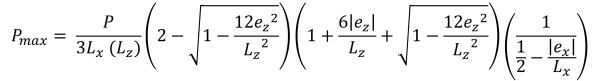
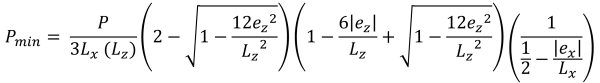
台形圧縮領域の水平底辺 (美しい & 痕跡, 2017):
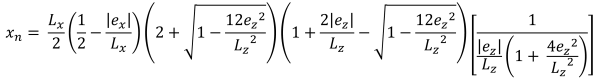
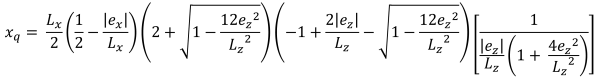
| 偏心によるコーナー圧力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| eバツ(+), eと(+) | P最高 | P分 | 0 | 0 |
| eバツ(+), eと(-) | P分 | P最高 | 0 | 0 |
| eバツ(-), eと(-) | 0 | 0 | P最高 | P分 |
| eバツ(-), eと(+) | 0 | 0 | P分 | P最高 |
ゾーンB (五角形の圧縮ゾーン)
このケースは、フーチングに加えられた荷重により二次ゾーン内で適度な偏心が発生した場合に発生します。. ゾーン B でカバーされる領域は、ゾーン C の外側の 2 つの湾曲した側面と 1 つの平らな底面によって境界付けられます。. この場合, 五角形の圧縮領域が生成される, 基礎の角だけが土との接触を失います. しかしながら, 以下に提供される解決策は少し複雑で、コーナー圧力と x の数値的解決方法が必要です。 & 圧縮領域の y 切片.
コーナープレッシャー (美しい & 痕跡, 2017):
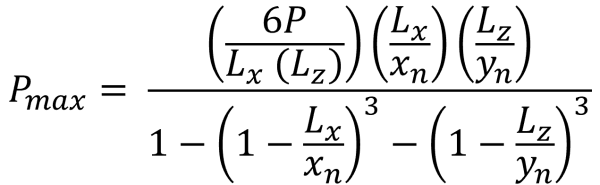
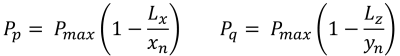
圧縮領域の五角形の辺 (美しい & 痕跡, 2017):
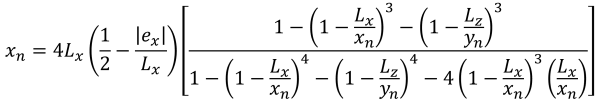
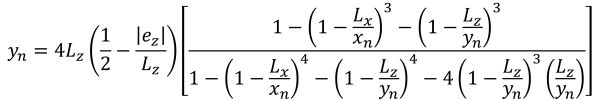

| 偏心によるコーナー圧力 | ||||
|---|---|---|---|---|
| P1 | P2 | P3 | P4 | |
| eバツ(+), eと(+) | P最高 | Pq | 0 | Pp |
| eバツ(+), eと(-) | Pp | P最高 | Pq | 0 |
| eバツ(-), eと(-) | 0 | Pp | P最高 | Pq |
| eバツ(-), eと(+) | Pq | 0 | Pp | P最高 |
あるいは, S.S によるより直接的な解決策. レイ (1995) 五角形の圧縮ゾーンのコーナー圧力と切片に使用できます。. 方程式を以下に示します。:
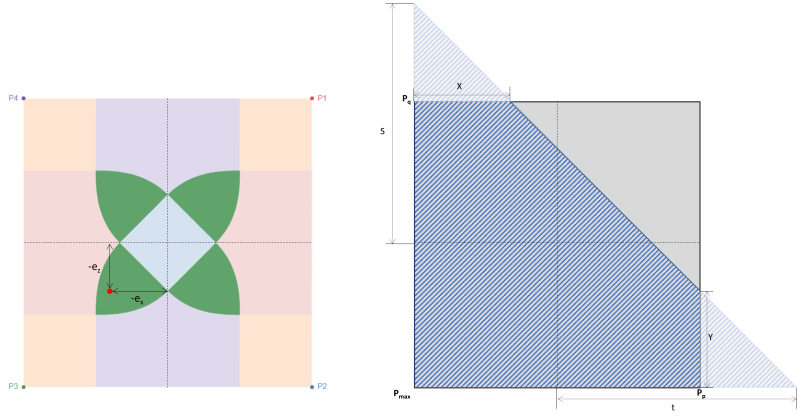
コーナープレッシャー (S.S.. レイ, 1995):
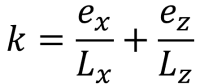


圧縮領域の五角形の辺 (S.S.. レイ, 1995):
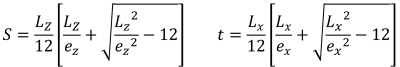
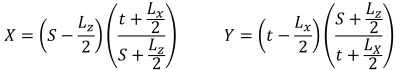
SkyCivの 基礎設計モジュール 長方形のコンクリート基礎の基礎圧力を解決できます。. さまざまな設計コードに従った追加の設計チェック (ACI 318-14, オーストラリアの標準 2009 & 2018, ユーロコード, そしてカナダの基準) もご利用いただけます.
最新のアップデート
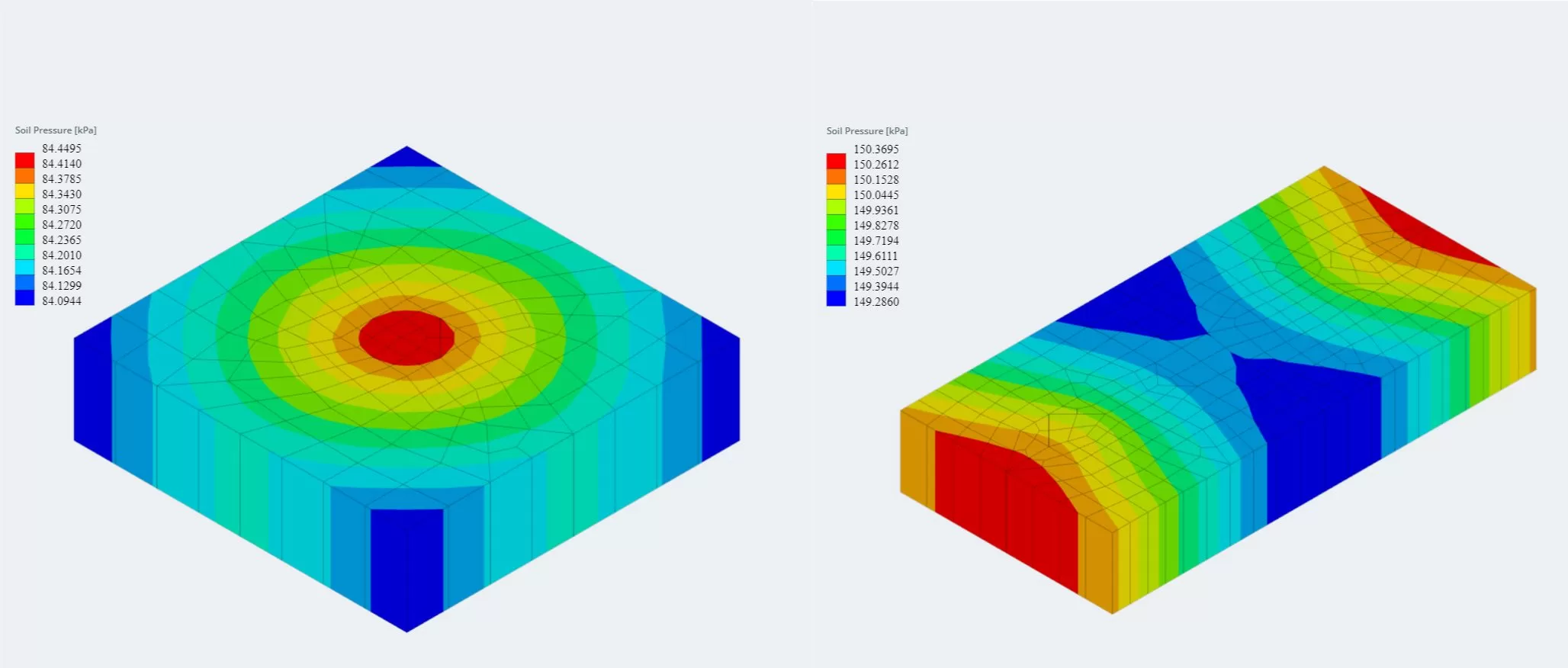
最新バージョンの基礎モジュールが有限要素解析と統合されました (醜い), これにより、より強力な土圧解析が可能になり、より詳細な曲げチェックに使用される木材アーマー解析が導入されます。. 土圧と木材アーマーモーメントの FEA 結果は 3D で表示でき、レポートに追加されました。.
SkyCivのFoundationDesignソフトウェアを試してみたい? 当社の無料ツールを使用すると、ユーザーは次のことを実行できます。 コンクリート基礎の計算 ダウンロードやインストールなしで!
参考文献:
- 美しい, J., 痕跡, N. (2017). 堅固な長方形の広がり基礎の下での線形土圧分布のための完全な解析ソリューション.
- それか, B.M. (2007). 基礎工学の原則 (7第版). グローバルエンジニアリング
- ラワット, S., など. アル. (2020). 二軸曲げによる孤立した長方形フーチング: 批判的な評価と簡素化された分析方法論.
- レイ, S.S.. (1995). 強化コンクリート. ブラックウェルサイエンス
製品開発者
BSc (民事), 修士課程 (民事)



