あ 複合基礎 2つ以上の柱をサポートする単一の基礎です. 結合されたフーチングは、列の間隔が狭すぎる場合に一般的に使用されます, 2つの孤立した足場では不十分な場合. 例えば, 互いに近すぎる2つの孤立した足場, 下の土壌は影響ゾーンの一部を共有する可能性があります, 分離されたフーチングのいずれかまたは両方の必要な拡張につながる. 物理的またはその他の制約に応じて, これは不可能かもしれません.

SkyCiv Foundation Designモジュールには、American ConcreteInstituteに準拠した複合フーチングの設計が含まれています (ACI 318).

SkyCivのFoundationDesignソフトウェアを試してみたい? 私たちの無料ツールを使用すると、ユーザーはダウンロードやインストールなしで耐荷重計算を実行できます!

基礎設計計算機

複合基礎の設計

寸法要件

孤立した基礎の寸法を決定するには, サービスまたはファクタリングされていない負荷, 死んだなど (D), 住む (L), 風 (W), 地震 (E), などは、荷重の組み合わせを使用して適用されます, ACIで定義されているとおり 318-14. どちらの荷重の組み合わせが支配するかは、設計荷重と見なされます, 式に示すように、許容土圧と比較されます 1, で推奨されているように セクション 13.2.6 ACIの 318-14.

\(\テキスト{q}_{\テキスト{a}} = frac{ \テキスト{P1}_{\テキスト{ん}} + \テキスト{P2}_{\テキスト{ん}} }{\テキスト{あ}} \右矢印 \) 方程式 1

どこ:
q_a =正味許容土圧
P1_ん =列での因数分解されていない荷重 1 (左)
P2_ん =列での因数分解されていない荷重 2 (正しい)
A =基礎エリア

方程式から 1, q_a との交換です あ.

\(\テキスト{あ} = frac{ \テキスト{P1}_{\テキスト{ん}} + \テキスト{P2}_{\テキスト{ん}} }{\テキスト{q}_{\テキスト{a}}} \右矢印 \) 式1a

この時点で, 基礎の寸法は、必要な面積の寸法から逆算できます。, あ.

一方向せん断

の 一方向せん断 限界状態, としても知られている “曲げせん断”, 基礎の幅全体にクリティカルセクションを拡張し、距離を置いて配置されます “d” 柱の表面から, 重要な平面せん断が配置されている場所 (図を参照してください 1).

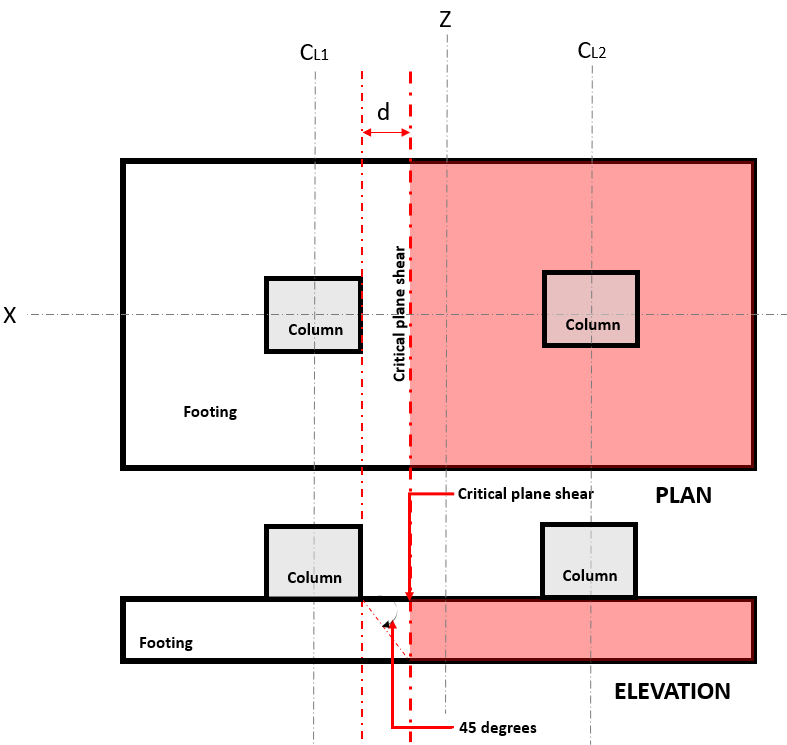
図 1. 一方向せん断の臨界面せん断

の 一方通行 剪断 要求する または V _あなた 基礎が、領域がある柱から片持ち梁で離れていると仮定して計算されます (赤) 図に示されている 1 に従って ACI 318-14, セクション 8.5.3.1.1.

の 一方向せん断耐力 または ϕV_c は極限せん断強度として定義され、式を使用して計算されます 2 あたり ACI 318-14, セクション 22.5.5.1:

\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 2 \平方根{\テキスト{f ’}_{\テキスト{c}}} \倍 text{b}_{\テキスト{w}} \倍 text{d} \右矢印 \) 方程式 2 (ACIEq。. 22.5.5.1 英語)

または

\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 0.17 \平方根{\テキスト{f ’}_{\テキスト{c}}} \倍 text{b}_{\テキスト{w}} \倍 text{d} \右矢印 \) 方程式 2 (ACIEq。. 22.5.5.1 メトリック)

どこ:
ϕ_剪断 =せん断設計係数
f’_c =指定されたコンクリート強度, psiまたはMPa
b_w =基礎の厚さ, インチまたはmm
d =極端な圧縮繊維から縦方向の張力補強の重心までの距離, インチまたはmm

ACIの設計要件を満たすには、せん断需要とせん断容量が次の式を満たす必要があります。 318-14:

\(\テキスト{V }_{\テキスト{あなた}} \leq phi text{V }_{\テキスト{c}} \右矢印 \) 方程式 3 (ACIEq。. 7.5.1.1(b))

SkyCiv Foundation, 式に準拠 3, 一方向せん断ユニティ比を計算します (方程式 4) せん断耐力よりもせん断需要をとることによって.

\( \テキスト{比} = frac{\テキスト{せん断需要}}{\テキスト{せん断耐力}} \右矢印 \) 方程式 4

双方向せん断

の 双方向せん断 限界状態, としても知られている “パンチングシアー”, クリティカルセクションを柱の面から「d / 2」の距離まで、柱の周囲に延長します。. 重要なせん断面は、基礎のそのセクションにあります (図を参照してください 2).

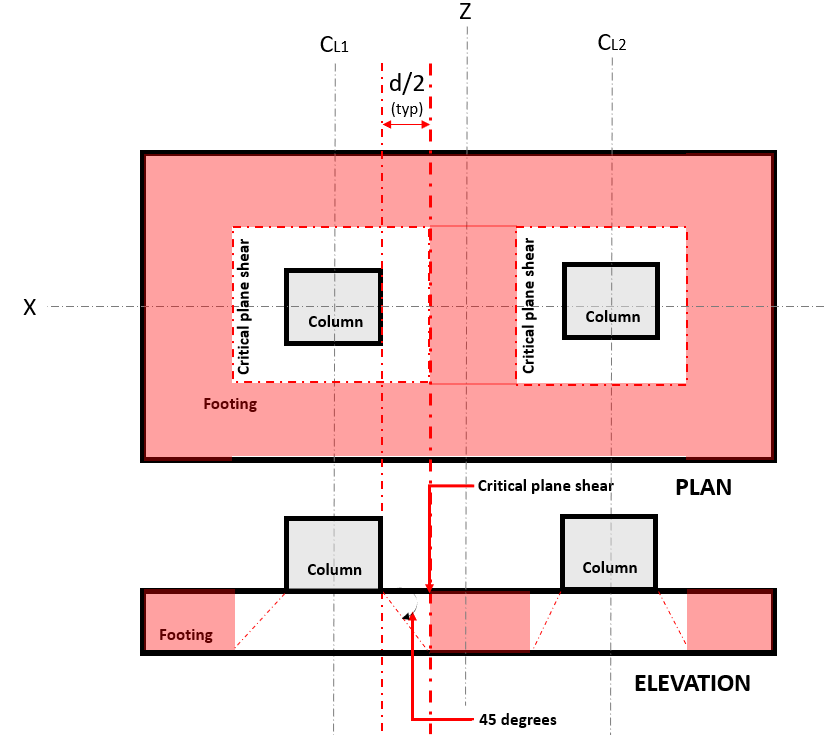
図 2. 二方向せん断の臨界面せん断

の ふたつのやり方需要を聞く または V _あなた 臨界せん断面で発生します, 「d / 2」の距離にあり、 (赤) ハッチングエリア, 図に示されている 2, に従って ACI 318-14, セクション 22.6.4.

の せん断耐力 または ϕV_c 式を使用して計算された最小値によって支配されます 5, 6, そして 7 あたり ACI 318-14, セクション 22.6.5.2:

\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 4 \倍ラムダ倍平方根{\テキスト{f ’}_{\テキスト{c}}} \右矢印 \) 方程式 5 (ACIEq。. 22.6.5.2(a) 英語)

\(\ファイテキスト{V }_{\テキスト{c}} = left ( 2 + \フラク{4}{\ベータ } \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 6 (ACIEq。. 22.6.5.2(b) 英語)

\(\ファイテキスト{V }_{\テキスト{c}} = left ( 2 + \フラク{\アルファ_{s} \倍d }{b{の}} \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 7 (ACIEq。. 22.6.5.2(c) 英語)

または

\(\ファイテキスト{V }_{\テキスト{c}} = phi _{\テキスト{剪断}} \回 0.33 \倍ラムダ倍平方根{\テキスト{f ’}_{\テキスト{c}}} \右矢印 \) 方程式 5 (ACIEq。. 22.6.5.2(a) メトリック)

\(\ファイテキスト{V }_{\テキスト{c}} = 0.17 \倍左 ( 1 + \フラク{2}{\ベータ } \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 6 (ACIEq。. 22.6.5.2(b) メトリック)

\(\ファイテキスト{V }_{\テキスト{c}} = 0.0083 \倍左 ( 2 + \フラク{\アルファ_{s} \倍d }{b{の}} \正しい ) \倍ラムダ倍平方根{f’_{c}} \右矢印 \) 方程式 7 (ACIEq。. 22.6.5.2(c) メトリック)

注意: βは、カラムの長辺と短辺の比率です。, 集中負荷, または反応面積とα_s 与えられます 22.6.5.3

どこ:
λ=同じ圧縮強度の通常の重量のコンクリートと比較して軽量コンクリートの機械的特性の低下を反映する修正係数
f’_c =指定されたコンクリート強度, psiまたはMPa
d =極端な圧縮繊維から縦方向の張力補強の重心までの距離, インチまたはmm

ACIの設計要件を満たすには、せん断需要とせん断容量が次の式を満たす必要があります。 318-14:

\(\テキスト{V }_{\テキスト{あなた}} \leq phi text{V }_{\テキスト{c}} \右矢印 \) 方程式 8 (ACIEq。. 7.5.1.1(b))

SkyCiv Foundation, 式に準拠 8, 双方向せん断ユニティ比を計算します (方程式 9) せん断耐力よりもせん断需要をとることによって.

\( \テキスト{比} = frac{\テキスト{せん断需要}}{\テキスト{せん断耐力}} \右矢印 \) 方程式 9

たわみ

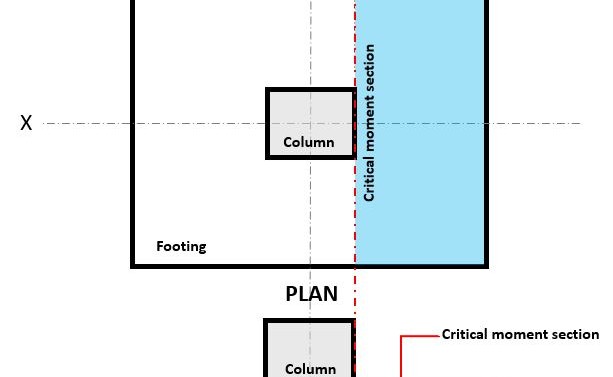
図 3. Flexureのクリティカルモーメントセクション

の 曲げ 限界状態はで発生します クリティカルフレクシャセクション, 基礎の上の柱の面にあります (図を参照してください 3).

の 曲げ需要, または M_あなた クリティカルフレクシャセクションにあります (青いハッチエリア) 図に示されている 3, 方程式を使用して計算されます 10:

\( \テキスト{M}_{あなた} = text{q}_{あなた} \倍左 ( \フラク{l_{バツ}}{2} – \フラク{c_{バツ}}{2} \正しい ) \倍l_{と} \倍左 ( \フラク{\フラク{l_{バツ}}{2} – \フラク{c_{バツ}}{2} }{2} \正しい ) \右矢印 \) 方程式 10

どこ:
q_あなた =因数分解された土壌圧力, ksfまたはkpa
l_バツ = x軸に平行な基礎寸法, インチまたはmm
l_と = z軸に平行な基礎寸法, インチまたはmm
c_バツ = x軸に平行な列の寸法, インチまたはmm

の 曲げ能力, または ϕMn 式を使用して計算されます 11:

\( \ファイテキスト{M}_{ん} = phi_{\テキスト{たわみ}} \倍A_{s} \倍f_{そして} \倍左( d – \フラク{a}{2} \正しい) \右矢印 \) 方程式 11

どこ:
ϕ =曲げ設計係数
l_バツ = x軸に平行な基礎寸法, インチまたはmm
l_と = z軸に平行な基礎寸法, インチまたはmm
d =極端な圧縮繊維から縦方向の張力補強の重心までの距離, インチまたはmm
あ_s =補強エリア, に² またはmm²
a =同等の長方形応力ブロックの深さ, インチまたはmm
fy =鋼の強度, ksiまたはMPa

参考文献

1. 構造コンクリートの建築基準要件 (ACI 318-14) 構造コンクリートの建築基準要件に関する解説 (ACI 318R-14). アメリカコンクリート学会, 2014.
2. マコーマック, ジャックC。, とラッセルH. 褐色. 鉄筋コンクリートACIの設計 318-11 コード版. ワイリー, 2014.
3. テイラー, アンドリュー, et al. 鉄筋コンクリート設計ハンドブック: ACI-318-14のコンパニオン. アメリカコンクリート学会, 2015.