AISCを使用したベースプレートのデザイン例 360-22 およびACI 318-19
問題ステートメント
設計されたカラムツーベースプレート接続が20キップの張力負荷に十分であるかどうかを判断します.
指定されたデータ
カラム:
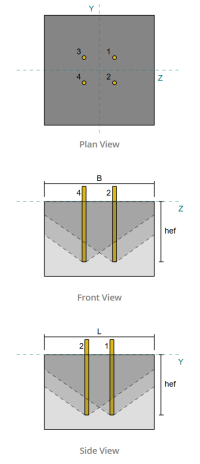
列セクション: W12x53
列エリア: 15.6 に2
列素材: A992
ベースプレート:
ベースプレートの寸法: 18 xで 18 に
ベースプレートの厚さ: 3/4 に
ベースプレート材料: A36
グラウト:
グラウトの厚さ: 1 に
コンクリート:
具体的な寸法: 22 xで 22 に
コンクリートの厚さ: 15 に
コンクリート材料: 4000 psi
ひび割れまたは破損していません: 割れた
アンカー:
アンカーの直径: 3/4 に
効果的な埋め込み長: 12 に
埋め込まれたプレート幅: 3 に
埋め込まれたプレートの厚さ: 1/4 に
列Webの表面からのアンカーオフセット距離: 2.8275 に
溶接:
溶接サイズ: 1/4 に
フィラー金属分類: E70XX
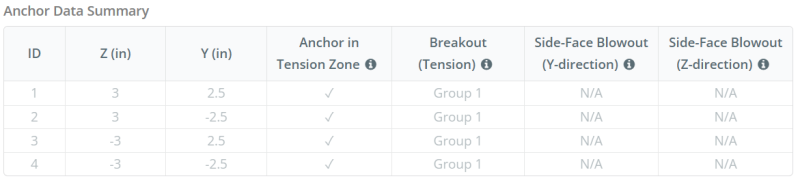
アンカーデータ (から SkyCIV計算機):
SkyCiv 無料ツールでモデルを作成する
無料のオンライン ツールを使用して、上記のベース プレート設計を今すぐモデル化してください。! サインアップは必要ありません.
定義
ロードパス:
ベースプレートが隆起にさらされるとき (引っ張り) 力, これらの力はアンカーロッドに伝達されます, これは、ベースプレートの曲げモーメントを誘発します. 曲げアクションは視覚化できます カンチレバーの曲げ 列セクションのフランジまたはウェブの周りに発生する, アンカーが配置されている場所に応じて.
構造が非線形の振る舞いを示す場合、非線形または2次の静的解析が適しています SkyCYVベースプレート設計ソフトウェア, 内部にあるアンカーのみ アンカーテンションゾーン 隆起に抵抗するのに効果的であると考えられています. このゾーンには通常、列のフランジまたはウェブの近くの領域が含まれます. このゾーンの外側のアンカーは張力抵抗に寄与せず、隆起の計算から除外されます.
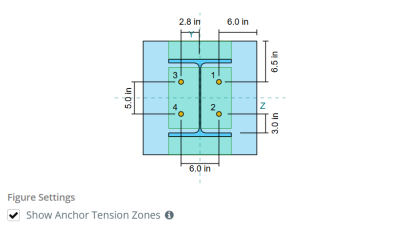
曲げに抵抗するベースプレートの有効な領域を決定する, a 45-度分散 各アンカーロッドの列面に向かっての中心線から想定されます. この分散は、を定義します 有効な溶接長 そして、それを確立するのに役立ちます 効果的な曲げ幅 プレートの.
仮定は、隆起力がプレートにどのように広がるかを近似することにより、ベースプレート分析を簡素化します.
アンカーグループ:
の SkyCYVベースプレート設計ソフトウェア どのアンカーが評価するためのアンカーグループの一部であるかを識別する直感的な機能が含まれています コンクリートブレイクアウト そして コンクリートシドE-Face Blowout 障害.
アン アンカーグループ 同様の効果的な埋め込み深度と間隔を持つ複数のアンカーで構成されています, そして、彼らに十分近い 投影抵抗領域が重複しています. アンカーがグループ化されたとき, それらの能力は、グループに適用される総張力力に抵抗するために組み合わされています.
グループ化基準を満たしていないアンカーは、 シングルアンカー. この場合, 個々のアンカーの張力のみが、それ自体の効果的な抵抗領域に対してチェックされます.
段階的な計算
小切手 #1: 溶接容量を計算します
始める, アンカーあたりの負荷とアンカーあたりの有効溶接長を計算する必要があります. 有効な溶接長は、 45°分散, 実際の溶接長とアンカー間隔によって制約されます.
この計算のために, アンカーはどちらにも分類されます アンカーを終了します または 中間アンカー. エンドアンカーは、アンカーの列または列の端にあります, 一方、中間アンカーはそれらの間に配置されます. 計算方法はそれぞれが異なり、列のジオメトリに依存します. この例では, ウェブには2つのアンカーがあります, 両方ともエンドアンカーに分類されます.
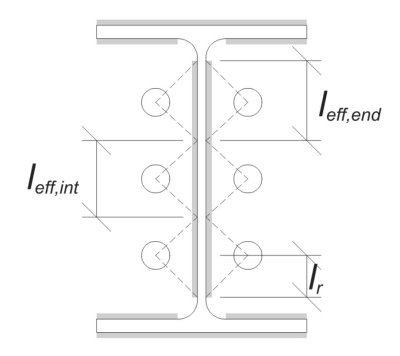
エンドアンカーの場合, 有効な溶接の長さは、アンカーの中心線からカラムのフィレットまでの利用可能な距離によって制限されます. 45°の分散は、この境界を超えて拡張してはなりません.
\(
l_r = frac{d_{col} – 2T_F – 2r_{col} – S_(n_{a,側} – 1)}{2} = frac{12.1 \, \テキスト{に} – 2 \回 0.575 \, \テキスト{に} – 2 \回 0.605 \, \テキスト{に} – 5 \, \テキスト{に} \回 (2 – 1)}{2} = 2.37 \, \テキスト{に}
\)
内側に, 有効な長さは、アンカー間隔の半分に制限されています. エンドアンカーの総有効溶接長は、外側と内側の長さの合計です.
\(
l_{eff,終わり} = min(する, 0.5S_) + \分(する, L_R)
\)
\(
l_{eff,終わり} = min(2.8275 \, \テキスト{に}, 0.5 \回 5 \, \テキスト{に}) + \分(2.8275 \, \テキスト{に}, 2.37 \, \テキスト{に}) = 4.87 \, \テキスト{に}
\)
この例では, の 最終的な有効溶接長 Webアンカーの場合、エンドアンカーの有効長と見なされます.
\(
l_{eff} = l_{eff,終わり} = 4.87 \, \テキスト{に}
\)
次, 計算しましょう アンカーごとの負荷. 4つのセットの場合 (4) アンカー, アンカーあたりの負荷はです:
\(
T_{あなた,アンカー} = frac{N_X}{n_{a,t}} = frac{20 \, \テキスト{キップ}}{4} = 5 \, \テキスト{キップ}
\)
計算された有効溶接長を使用します, これで決定できます 溶接に必要な単位長さあたりの力が必要です.
\(
r_u = frac{T_{あなた,アンカー}}{l_{eff}} = frac{5 \, \テキスト{キップ}}{4.87 \, \テキスト{に}} = 1.0267 \, \テキスト{kip/in}
\)
今, 我々は使用するだろう AISC 360-22, 第J2.4章 フィレット溶接の設計強度を計算します.
適用された負荷は純粋に軸方向の張力であるためです, 角度 \(\theta ) 90°と見なされます, 方向性強度係数KDSは、 AISC 360-22 Eq. J2-5.
\(
k_{DS} = 1.0 + 0.5(\それなし(\シータ))^{1.5} = 1 + 0.5 \回 (\それなし(1.5708))^{1.5} = 1.5
\)
最後に, 私たちは適用します AISC 360-22 Eq. J2-4 を決定する ユニットの長さあたりのフィレット溶接の設計強度.
\(
\phi r_n = phi 0.6 F_{exx} E_{w,ウェブ} k_{DS} = 0.75 \回 0.6 \回 70 \, \テキスト{KSI} \回 0.177 \, \テキスト{に} \回 1.5 = 8.3633 \, \テキスト{kip/in}
\)
以来 1.0267 KPI < 8.3633 KPI, 溶接容量はです 十分な.
小切手 #2: 張力負荷によるベースプレートの曲げ容量を計算する
tを使用します彼はアンカーごとにロードし、Oアンカーの中心から列の表面までのffset距離 (負荷の偏心として機能します), ベースプレートに適用される瞬間は、 カンチレバー 予測.
\(
M_U = T_{あなた,\テキスト{アンカー}} e = 5 \, \テキスト{キップ} \回 2.8275 \, \テキスト{に} = 14.137 \, \テキスト{キップ} \CDOT テキスト{に}
\)
次, 計算を使用しますd有効な溶接長m曲げ幅としての前のチェック, を計算できます 上部構造荷重からのスプレッドフーチングを設計するための設計モジュールです。 使用しているベースプレートの AISC 360-22, 方程式 2-1:
\(
\non -m_n = phi f_{そして,\テキスト{血圧}} Z_{\テキスト{eff}} = 0.9 \回 36 \, \テキスト{KSI} \回 0.68484 \, \テキスト{に}^3 = 22.189 \, \テキスト{キップ} \CDOT テキスト{に}
\)
どこ,
\(
Z_{\テキスト{eff}} = frac{l_{\テキスト{eff}} (t_{\テキスト{血圧}})^ 2}{4} = frac{4.87 \, \テキスト{に} \回 (0.75 \, \テキスト{に})^ 2}{4} = 0.68484 \, \テキスト{に}他のいくつかの例は
\)
以来 14.137 チキンイン < 22.189 チキンイン, ベースプレートの曲げ容量はです 十分な.
小切手 #3: アンカーロッド引張容量を計算します
アンカーロッドの引張容量を評価します, 我々は使用するだろう ACI 318-19 方程式 17.6.1.2.
最初, を決定します 指定された引張強度 アンカー鋼の. これは、許可されている最低値です ACI 318-19 句 17.6.1.2, 材料特性を参照して AISC 360-22 表J3.2.
\(
f_{\テキスト{uta}} = min left( 0.75 F_{あなた,\テキスト{anc}}, 1.9 F_{そして,\テキスト{anc}}, 125 \正しい) = min left( 0.75 \回 120 \, \テキスト{KSI}, 1.9 \回 92 \, \テキスト{KSI}, 125.00 \, \テキスト{KSI} \正しい) = 90 \, \テキスト{KSI}
\)
次, を計算します 効果的な断面領域 アンカーロッドの. これはに基づいています ACI 318-19 解説条項R17.6.1.2, スレッドジオメトリを説明します. インチあたりのスレッド数は取得されます ASME B1.1-2019テーブル 1.
\(
A_{知っている,N} = frac{\パイ}{4} \左( D_A – \フラク{0.9743}{N_T} \正しい)^2 = frac{\パイ}{4} \倍左( 0.75 \, \テキスト{に} – \フラク{0.9743}{10 \, \テキスト{に}^{-1}} \正しい)^2 = 0.33446 \, \テキスト{に}^ 2
\)
これらの値で, 適用します ACI 318-19 方程式 17.6.1.2 を計算します 引張強度を設計します アンカーロッドの.
\(
\ファイN_{に} = phi A_{知っている,N} f_{\テキスト{uta}} = 0.75 \回 0.33446 \, \テキスト{に}^2 Times 90 \, \テキスト{KSI} = 22.576 \, \テキスト{キップ}
\)
以前に計算されたことを思い出してください アンカーあたりの張力負荷:
\(
N_{する} = frac{N_X}{n_{a,t}} = frac{20 \, \テキスト{キップ}}{4} = 5 \, \テキスト{キップ}
\)
以来 5 キップ < 22.576 キップ, アンカーロッド引張容量はです 十分な.
小切手 #4: コンクリートのブレイクアウト容量を緊張して計算します

ブレイクアウト容量を計算する前, 最初にメンバーが資格を得るかどうかを判断する必要があります 狭いメンバー. による ACI 318-19 句 17.6.2.1.2, メンバーは、狭いメンバーの基準を満たしています. したがって, 計算では、修正された有効埋め込み長を使用する必要があります.
それは 修正された有効埋め込み長, H’EF, アンカーグループの:
\(
H’_{\テキスト{ef}} = 5.667 \, \テキスト{に}
\)
使用する ACI 318-19 句 17.6.2, を計算します 最大投影コンクリートコーンエリア 単一のアンカーの場合, 修正された有効埋め込み長に基づいています.
\(
A_{N_{co}} = 9 \左( H’_{ef,G1} \正しい)^2 = 9 \倍左( 5.6667 \, \テキスト{に} \正しい)^2 = 289 \, \テキスト{に}^ 2
\)
同様に, 修正された有効埋め込み長を使用して、 実際に投影されたコンクリートコーンエリア アンカーグループの.
\(
A_{N_C} = min left( n_{a,G1} A_{N_{co}}, L_{N_C} b_{N_C} \正しい) = min left( 4 \回 289 \, \テキスト{に}^ 2, 22 \, \テキスト{に} \回 22 \, \テキスト{に} \正しい) = 484 \, \テキスト{に}^ 2
\)
どこ,
\(
L_{N_C} = min left( c_{\テキスト{左},G1}, 1.5 H’_{\テキスト{ef},G1} \正しい)
+ \左( \min 左( S_{\テキスト{和},と,G1}, 3 H’_{\テキスト{ef},G1} \左( n_{と,G1} – 1 \正しい) \正しい) \正しい)
+ \min 左( c_{\テキスト{正しい},G1}, 1.5 H’_{\テキスト{ef},G1} \正しい)
\)
\(
L_{N_C} = min left( 8 \, \テキスト{に}, 1.5 \回 5.6667 \, \テキスト{に} \正しい)
+ \左( \min 左( 6 \, \テキスト{に}, 3 \回 5.6667 \, \テキスト{に} \倍左( 2 – 1 \正しい) \正しい) \正しい)
+ \min 左( 8 \, \テキスト{に}, 1.5 \回 5.6667 \, \テキスト{に} \正しい)
\)
\(
L_{N_C} = 22 \, \テキスト{に}
\)
\(
b_{N_C} = min left( c_{\テキスト{上},G1}, 1.5 H’_{\テキスト{ef},G1} \正しい)
+ \左( \min 左( S_{\テキスト{和},そして,G1}, 3 H’_{\テキスト{ef},G1} \左( n_{そして,G1} – 1 \正しい) \正しい) \正しい)
+ \min 左( c_{\テキスト{底},G1}, 1.5 H’_{\テキスト{ef},G1} \正しい)
\)
\(
b_{N_C} = min left( 8.5 \, \テキスト{に}, 1.5 \回 5.6667 \, \テキスト{に} \正しい)
+ \左( \min 左( 5 \, \テキスト{に}, 3 \回 5.6667 \, \テキスト{に} \倍左( 2 – 1 \正しい) \正しい) \正しい)
+ \min 左( 8.5 \, \テキスト{に}, 1.5 \回 5.6667 \, \テキスト{に} \正しい)
\)
\(
b_{N_C} = 22 \, \テキスト{に}
\)
次, を評価します 基本的なコンクリートブレイクアウト強度 使用した単一のアンカーの ACI 318-19 句 17.6.2.2.1
\(
N_b = k_c lambda_a sqrt{\フラク{f’_c}{\テキスト{psi}}} \左( \フラク{H’_{\テキスト{ef},G1}}{\テキスト{に}} \正しい)^{1.5} \, \テキスト{lbf}
\)
\(
N_b = 24 \回 1 \回 sqrt{\フラク{4 \, \テキスト{KSI}}{0.001 \, \テキスト{KSI}}} \倍左( \フラク{5.6667 \, \テキスト{に}}{1 \, \テキスト{に}} \正しい)^{1.5} \回 0.001 \, \テキスト{キップ} = 20.475 \, \テキスト{キップ}
\)
どこ,
- \(k_{c} = 24\) キャストインアンカー用
- \(\lambda = 1.0 \) 通常の体重コンクリート用
今, 計算することにより、ジオメトリの効果を評価します エッジ効果係数 そしてその 偏心因子.
アンカーグループの最短エッジ距離は、:
\(
c_{a,\テキスト{分}} = min left( c_{\テキスト{左},G1}, c_{\テキスト{正しい},G1}, c_{\テキスト{上},G1}, c_{\テキスト{底},G1} \正しい)
= min left( 8 \, \テキスト{に}, 8 \, \テキスト{に}, 8.5 \, \テキスト{に}, 8.5 \, \テキスト{に} \正しい) = 8 \, \テキスト{に}
\)
による ACI 318-19 句 17.6.2.4.1, ブレイクアウト エッジ効果係数 です:
\(
\psi_{ed,N} = min left( 1.0, 0.7 + 0.3 \左( \フラク{c_{a,\テキスト{分}}}{1.5 H’_{\テキスト{ef},G1}} \正しい) \正しい)
= min left( 1, 0.7 + 0.3 \倍左( \フラク{8 \, \テキスト{に}}{1.5 \回 5.6667 \, \テキスト{に}} \正しい) \正しい) = 0.98235
\)
張力負荷はアンカーグループの重心に適用されるため, 偏心はゼロです. したがって, の 偏心因子, 節からも 17.6.2.4.1, です:
\(
\psi_{ec,N} = min left( 1.0, \フラク{1}{1 + \フラク{2 および ’_N}{3 H’_{\テキスト{ef},G1}}} \正しい)
= min left( 1, \フラク{1}{1 + \フラク{2 \回 0}{3 \回 5.6667 \, \テキスト{に}}} \正しい) = 1
\)
加えて, 両方の ひび割れ係数 そしてその 分割係数 と見なされます:
\(
\psi_{c,N} = 1
\)
\(
\psi_{cp,N} = 1
\)
その後, これらすべての要因を組み合わせて使用します ACI 318-19 Eq. 17.6.2.1b を評価する アンカーグループのコンクリートブレイクアウト強度:
\(
\ファイN_{cbg} = phi 左( \フラク{A_{N_C}}{A_{N_{co}}} \正しい) \psi_{ec,N} \psi_{ed,N} \psi_{c,N} \psi_{cp,N} N_b
\)
\(
\ファイN_{cbg} = 0.7 \倍左( \フラク{484 \, \テキスト{に}^ 2}{289 \, \テキスト{に}^ 2} \正しい) \回 1 \回 0.98235 \回 1 \回 1 \回 20.475 \, \テキスト{キップ} = 23.58 \, \テキスト{キップ}
\)
の 総張力負荷 アンカーグループには、個々のアンカー負荷の産物とアンカーの数があります:
\(
N_{する} = left( \フラク{N_X}{n_{a,t}} \正しい) n_{a,G1} = left( \フラク{20 \, \テキスト{キップ}}{4} \正しい) \回 4 = 20 \, \テキスト{キップ}
\)
以来 20 キップ < 23.58 キップ, 具体的なブレイクアウト容量はです 十分な.
小切手 #5: アンカープルアウト容量を計算します
アンカーの引き抜き容量は、その埋め込まれた端での抵抗によって支配されます. 始める, 埋め込まれたプレートのベアリング領域を計算します, アンカーロッドで占有されている領域を差し引いた後のネットエリアです.
長方形の埋め込みプレート用, の ベアリングエリア として計算されます:
\(
A_{brg} = left( \左( =最も近いサポートの面までのせん断が考慮されているセクションの距離{埋め込み _plate} \正しい)^2 右) – A_{ロッド} = left( \左( 3 \, \テキスト{に} \正しい)^2 右) – 0.44179 \, \テキスト{に}^2 = 8.5582 \, \テキスト{に}^ 2
\)
どこ,
\(
A_{ロッド} = frac{\パイ}{4} \左( d_a 右)^2 = frac{\パイ}{4} \倍左( 0.75 \, \テキスト{に} \正しい)^2 = 0.44179 \, \テキスト{に}^ 2
\)
次, を決定します 基本的なアンカープルアウト強度 を使用して ACI 318-19 式17.6.3.2.2a.
\(
N_b = 8 A_{brg} \左( f’_c 右) = 8 \回 8.5582 \, \テキスト{に}^2 times 左( 4 \, \テキスト{KSI} \正しい) = 273.86 \, \テキスト{キップ}
\)
次に、適切な抵抗係数を適用します 引き出し亀裂係数:
- ために 割れた コンクリート, \(\psi_{cp} = 1.0\)
- ために クラッキングされていません コンクリート, \(\psi_{cp} = 1.4\)
これらを使用します, 計算します 緊張の中でアンカーの引き抜き強度を設計します あたり ACI 318-19 方程式 17.6.3.1.
\(
\ファイN_{pn} = phi psi_{c,p} N_b = 0.7 \回 1 \回 273.86 \, \テキスト{キップ} = 191.7 \, \テキスト{キップ}
\)
以前に計算されたことを思い出してください アンカーあたりの張力負荷:
\(
N_{する} = frac{N_X}{n_{a,t}} = frac{20 \, \テキスト{キップ}}{4} = 5 \, \テキスト{キップ}
\)
以来 5 キップ < 191.7 キップ, アンカープルアウト容量はです 十分な.
小切手 #6: 埋め込みプレートの曲げ能力を計算します
これは、を使用して実行される補足チェックです SkyCYVベースプレート設計ソフトウェア 埋め込まれたプレートに十分な曲げ能力があり、印加されたプルアウト荷重の下で生成されないことを確認するために.
最初, 自由の長さを決定します (サポートされていません) 埋め込まれたプレートの端, サポートの端からロッドの表面への測定.
\(
b’ = frac{=最も近いサポートの面までのせん断が考慮されているセクションの距離{埋め込み _plate} – D_A}{2} = frac{3 \, \テキスト{に} – 0.75 \, \テキスト{に}}{2} = 1.125 \, \テキスト{に}
\)
次, を計算します 曲げモーメント 均一なベアリング圧力によって誘発されます. この圧力は、アンカープルアウトアクションから埋め込みプレートに移動した力を表します.
\(
m_f = frac{\左( \フラク{T_A}{A_{brg}} \正しい) \左( b’ \正しい)^ 2}{2} = frac{\左( \フラク{5 \, \テキスト{キップ}}{8.5582 \, \テキスト{に}^ 2} \正しい) \倍左( 1.125 \, \テキスト{に} \正しい)^ 2}{2} = 0.36971 \, \テキスト{キップ}
\)
最後に, 計算されたモーメントを使用し、与えられた材料特性を使用します, を決定します 必要なプレートの最小厚さ 抵抗する 屈曲収量.
\(
t_{分} = sqrt{\フラク{4 M_F}{\phi f_{y _ep}}} = sqrt{\フラク{4 \回 0.36971 \, \テキスト{キップ}}{0.9 \回 36 \, \テキスト{KSI}}} = 0.21364 \, \テキスト{に}
\)
実際の埋め込みプレートの厚さを思い出してください:
\(
t_{実際の} = T_{埋め込み _plate} = 0.25 \, \テキスト{に}
\)
以来 0.21364 に < 0.25 に, 埋め込まれたプレートの曲げ能力はです 十分な.
小切手 #7: y方向のサイドフェイスブローアウト容量を計算します
この計算は、この例には適用されません, で指定された条件として ACI 318-19 句 17.6.4 満たされていません. したがって, Y方向に沿ったサイドフェイスブローアウト障害は発生しません.
小切手 #8: Z方向のサイドフェイスブローアウト容量を計算します
この計算は、この例には適用されません, で指定された条件として ACI 318-19 句 17.6.4 満たされていません. したがって, Z方向に沿ったサイドフェイスブローアウト障害は発生しません.
設計の概要
の SkyCYVベースプレート設計ソフトウェア このデザインの例の段階的な計算レポートを自動的に生成できます. また、実行されたチェックとその結果の比率の概要も提供します, 情報を一目で理解しやすくします. 以下はサンプルの概要表です, レポートに含まれています.
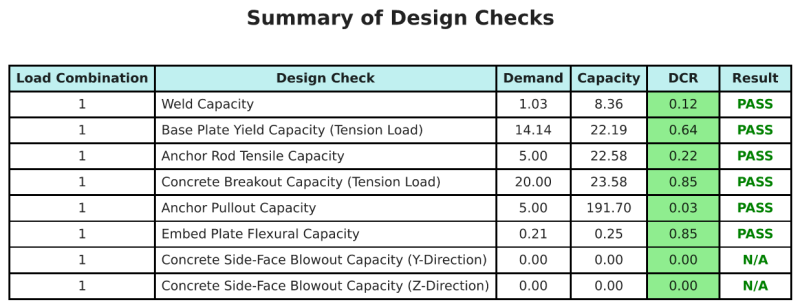
SkyCIVサンプルレポート
SkyCiv ベース プレート設計レポートから期待できる詳細レベルと明瞭さのレベルを確認してください。. The report includes all key design checks, 方程式, 結果は明確で読みやすい形式で表示されます. It is fully compliant with design standards. SkyCiv ベース プレート カリキュレーターを使用して生成されたサンプル レポートを表示するには、以下をクリックしてください。.
ベースプレートソフトウェアを購入します
他のSkyCIVモジュールなしで、ベースプレートデザインモジュールのフルバージョンを単独で購入する. これにより、ベースプレートデザインの完全な結果が得られます, 詳細なレポートとその他の機能を含む.