Fondamenti del momento di inerzia

Il momento di inerzia può essere derivato ottenendo il il momento di inerzia delle parti e applicando la formula di trasferimento: Io = io₀ + Anno Domini². Abbiamo un articolo completo che spiega l'approccio a risolvere il momento d'inerzia.

fondamentalmente, il momento di inerzia è il secondo momento dell'area, che può essere espresso come segue:

[matematica] IO_{x}= int int y ^{2}dà [matematica] [matematica] IO_{y}= int int x ^{2}dà [matematica]

Per osservare la derivazione delle formule seguenti, proviamo a trovare il momento di inerzia di un oggetto come un rettangolo attorno al suo asse maggiore usando solo la formula sopra. Per ottenere il momento di inerzia, i limiti devono essere determinati in modo tale da essere presi dall'asse di rotazione alla sua fibra estrema. Questi sarebbero i limiti dell'integrale esterno. L'integrale interno ha un limite da 0 essere. Detto ciò, possiamo anche esprimere dA come xdy, che diventerà bdy. Poiché l'asse di rotazione è sull'asse neutro, il momento di inerzia può essere integrato con un limite superiore di h / 2 e un limite inferiore di 0 e moltiplicato due volte a causa della simmetria del rettangolo. Questo ci lascia con l'integrale di seguito.

[matematica] IO_{x}= 2 int_{0}^{\frac{h}{2}} e ^{2}bdy [matematica] Integrare, [matematica] IO_{x}= 2b sinistra [ \frac{e ^{3}}{3} \giusto ]_{0}^{\frac{h}{2}} [matematica] [matematica] IO_{x}= 2b sinistra [ \frac{h ^{3}}{24}-0 \giusto ] [matematica] [matematica] IO_{x}= Frac{bh ^{3}}{12} [matematica]

Formula del momento d'inerzia per sezioni di trave

Formula del momento d'inerzia per sezioni di trave (secondo momento dell'area). Le equazioni del momento d'inerzia sono estremamente utili per calcoli rapidi e precisi. Le formule sono state riassunte nelle loro forme più semplici per tua comodità.

SkyCiv offre anche a Calcolatore gratuito del momento d’inerzia per calcoli rapidi o per verificare di aver applicato correttamente la formula. La formula del momento di inerzia per il rettangolo, cerchio, Formula del momento d'inerzia per sezioni di trave. Formula del momento d'inerzia per sezioni di trave:

• Il momento di inerzia dell'area è diverso dal momento di inerzia della massa
• È anche conosciuto come il secondo momento dell'area
• È un fattore significativo di deflessione (maggiore è l'io_x, la deflessione inferiore sarà)
• Le unità sono lunghe alla potenza di 4
• Le seguenti equazioni danno il momento di inerzia rispetto al baricentro della sezione

RIFERIMENTO	Ixx	Iyy
Equazione del momento di inerzia per sezioni rettangolari o rettangolari
	[matematica] \dfrac{bh ^ 3}{12} [matematica]	[matematica] \dfrac{b ^{3}h}{12} [matematica]
Equazione del momento di inerzia per una sezione rettangolare cava
	[matematica] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [matematica]	[matematica] \dfrac{b ^ 3h}{12} – \dfrac{b_1 ^ 3h_1}{12} [matematica]
Equazione del momento di inerzia per un cerchio o una sezione circolare
	[matematica] \dfrac{\pi}{64}D ^ 4 [matematica]	[matematica] \dfrac{\pi}{64}D ^ 4 [matematica]
Equazione del momento di inerzia per una sezione circolare cava
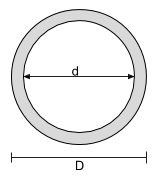	[matematica] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [matematica]	[matematica] \dfrac{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [matematica]
Equazione del momento di inerzia per un triangolo isoscele
	[matematica] \dfrac{bh ^ 3}{36} [matematica]	[matematica] \dfrac{3b ^ 3h}{144} [matematica]
Equazione del momento di inerzia di una sezione a I.
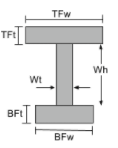	[matematica] \frac{TFw times TFt ^{3}}{12} +\frac{Wt volte Wh ^{3}}{12} + \frac{BFw times BFt ^{3}}{12} +[matematica] [matematica] TFw times TFt times left ( Bft + Wh + frac{Tft}{2} -\bar{y}_{bot} \giusto )^{2} +[matematica] [matematica] Wt times Wh times left ( BFt + frac{Wh}{2} -\bar{y}_{bot} \giusto )^{2} +[matematica] [matematica] BFw times BFt times left ( \frac{Wh}{2} -\bar{y}_{bot} \giusto )^{2} [matematica]	[matematica] \frac{TFt volte TFw ^{3}}{12} + \frac{Wh volte Wt ^{3}}{12} + \frac{BFt times BFw ^{3}}{12} [matematica]
Equazione del momento di inerzia di una sezione a T.
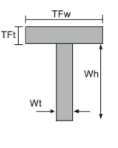	[matematica] \frac{TFw times TFt ^{3}}{12} + \frac{Wt volte Wh ^{3}}{12} +[matematica] [matematica] TFw times TFt left ( Wh + \frac{Tft}{2} -\bar{y}_{bot} \giusto )^{2} +[matematica] [matematica] Wt times Wh times left ( \frac{Wh}{2} – \bar{y}_{bot} \giusto )^{2} [matematica]	[matematica] \frac{TFt volte TFw ^{3}}{12} + \frac{Wh volte Wt ^{3}}{12} [matematica]
Equazione del momento di inerzia di una sezione di canale
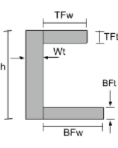	[matematica] \frac{TFw times TFt ^{3}}{12} + \frac{BFw times BFt ^{3}}{12} + \frac{Wt volte h ^{3}}{12} +[matematica] [matematica] TFw times TFt times left ( h – \frac{Tft}{2} – \bar{y}_{bot} \giusto )^{2} +[matematica] [matematica] BFw times BFt times left ( \frac{Bft}{2} – \bar{y}_{bot} \giusto )^{2} +[matematica] [matematica] Wt times h times left ( \frac{h}{2} – \bar{y}_{bot} \giusto )^{2} [matematica]	[matematica] \frac{TFt volte TFw ^{3}}{12} + \frac{BFt times BFw ^{3}}{12} + \frac{h volte Wt ^{3}}{12} +[matematica] [matematica] TFt times TFw times left ( wt + \frac{TFW}{2} – \bar{x}_{sinistra} \giusto )^{2} +[matematica] [matematica] BFt times BFw times left ( wt + \frac{BFW}{2} – \bar{x}_{sinistra} \giusto )^{2} +[matematica] [matematica] h times Wt times left ( \frac{wt}{2} – \bar{x}_{sinistra} \giusto )^{2} [matematica]
Momento di inerzia equazione degli angoli
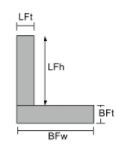	[matematica] \frac{BFw times BFt ^{3}}{12} + \frac{ LFt times LFh ^{3}}{12} +[matematica] [matematica] BFw times BFt times left ( \frac{Bft}{2}-\bar{y}_{bot} \giusto )^{2} +[matematica] [matematica] LFt times LFh times left ( Bft + \frac{LFH}{2}-\bar{y}_{bot} \giusto )^{2} [matematica]	[matematica] \frac{BFt times BFw ^{3}}{12} + \frac{ LFh times LFt ^{3}}{12} +[matematica] [matematica] BFt times BFw times left ( \frac{BFW}{2}-\bar{x}_{sinistra} \giusto )^{2} +[matematica] [matematica] LFh times LFt times left ( \frac{LFt}{2}-\bar{x}_{sinistra} \giusto )^{2} [matematica]

Usa SkyCiv Section Builder per i calcoli manuali

In questo articolo, ti abbiamo guidato attraverso la formula del momento di inerzia. Per ulteriori informazioni su questo argomento, visita il nostro tutorial su Momento d'inerzia della sezione della trave.

Lo sapevate Il Generatore di Sezioni SkyCiv mostra anche i calcoli a mano intera per le seguenti forme?

• Rettangolare, Rettangolare vuoto
• Circolare, Circolare cava
• I-Beam, T-Beam
• Angolo (L-Beam), o scanalatura
• Sezioni triangolari

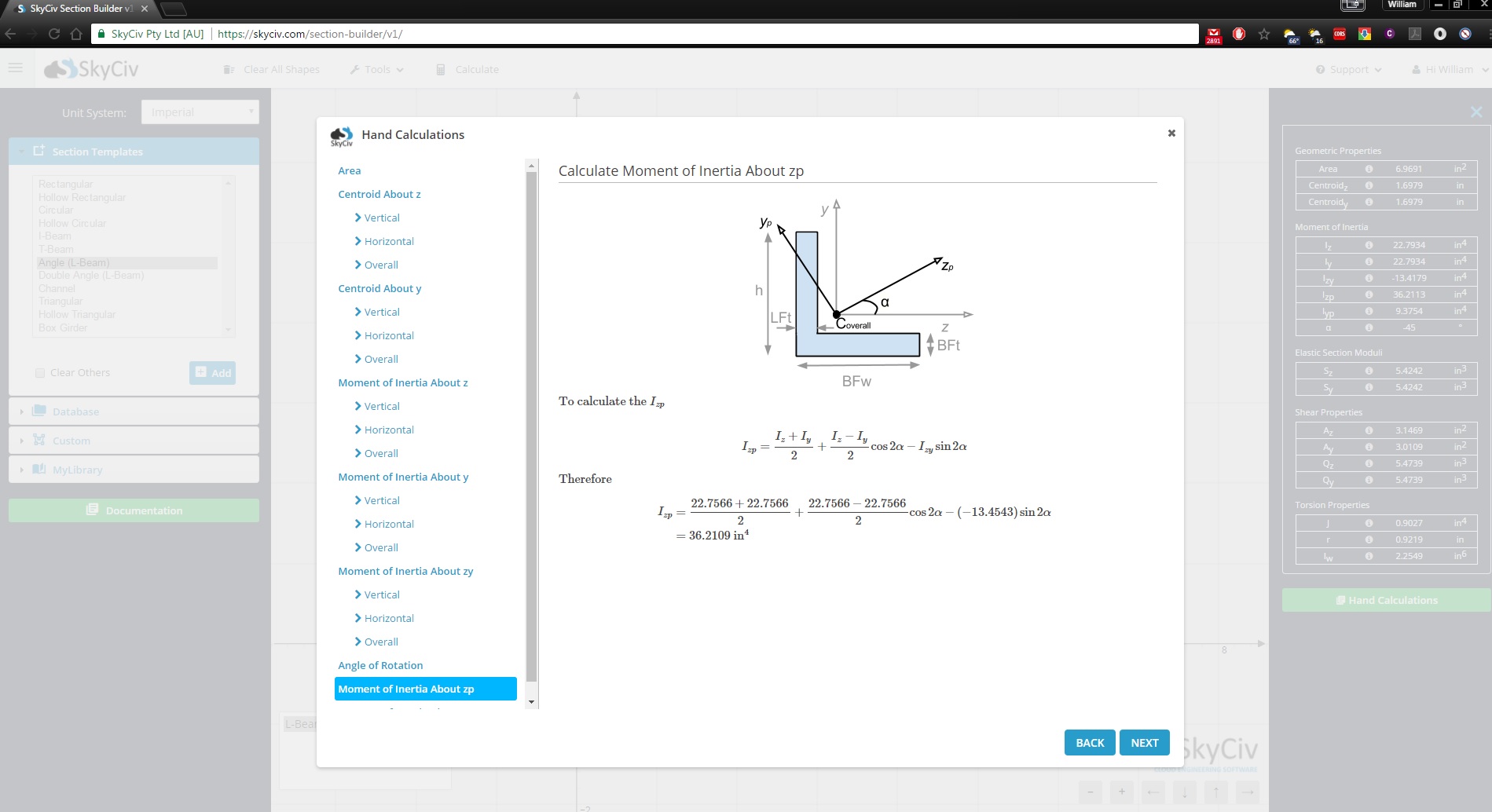
Ci auguriamo che la tabella sopra riportata sia utile per calcolare un momento di inerzia di un cerchio, triangolo, e momento di inerzia del rettangolo tra le altre forme. Abbiamo anche un utile Momento di inerzia calcolatrice, un semplificato di Il Generatore di Sezioni SkyCiv, che gestisce questi calcoli per te o registrati oggi per iniziare con il software SkyCiv!