Il momento di inerzia è un'importante proprietà geometrica utilizzata nell'ingegneria strutturale. È direttamente correlato alla quantità di resistenza materiale della sezione. Generalmente, un momento d'inerzia maggiore implica una maggiore resistenza nella sezione, con conseguente riduzione della deflessione quando sottoposto a un carico. La designazione “il momento di inerzia” è in realtà un termine improprio ampiamente utilizzato, poiché questa proprietà non ha nulla a che fare con l'inerzia. Il nome tecnico corretto è in realtà Secondo momento d'area. Questa designazione descrive più accuratamente ciò che viene misurato in questa proprietà, che può essere considerato approssimativamente come una misura di quanto l'area della sezione è lontana dall'asse neutro.

Tabella dei contenuti

• Momento di inerzia di una formula rettangolare
• Sezioni cave rettangolari (RHS)

Momento di inerzia di una formula rettangolare

La formula generale utilizzata per determinare il momento d'inerzia di un rettangolo è:

[matematica] IO_{xx}= dfrac{BD^3}{12} , IO_{yy}= dfrac{B^3D}{12} [matematica]

Dove il xx e yy fare riferimento all'asse particolare, o direzione, essere considerato.

È una convenzione comune di ingegneria strutturale che B si riferisce a larghezza del rettangolo, parallelo a un convenzionalmente orizzontale asse x.

Allo stesso modo, D si riferisce a profondità del rettangolo, parallelo a un convenzionalmente verticale asse y.

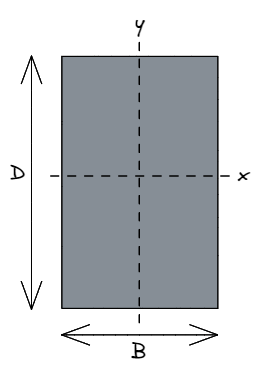
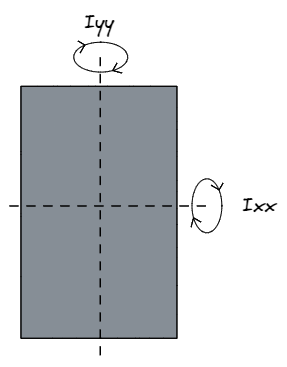
Quando gli ingegneri strutturali si riferiscono a Ixx fanno riferimento alla forza di una sezione di l'asse x, significato in una direzione parallela al D dimensione, o asse y. Allo stesso modo, Aaaaaaaaaaaaaaaaaaaaaaaa si riferisce alla forza di l'asse y, significato in una direzione parallela al B dimensione, o asse x.

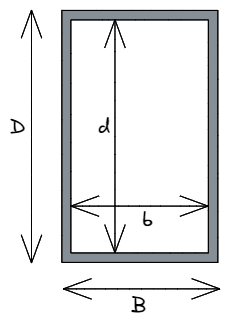
Sezioni cave rettangolari (RHS)

Mentre gli ingegneri potrebbero ipoteticamente utilizzare sezioni rettangolari solide durante la progettazione, ciò consumerebbe una quantità significativamente maggiore di materia prima, con relativi incrementi di peso e di costo. È molto più comune usare rettangolare sezioni cave (comunemente indicato come an RHS). Qui possiamo utilizzare la stessa equazione definita sopra per il caso rettangolare generale, però, dobbiamo sottrarre l'interno vuoto area del rettangolo:

[matematica] IO_{xx}= dfrac{BD^3}{12} – \dfrac{bd^3}{12} [matematica]

In questo caso, minuscolo b e d denotiamo la dimensione dell'area vuota all'interno del rettangolo che dobbiamo sottrarre dalle dimensioni esterne della forma, essere maiuscolo B e D. La differenza tra ciascuna dimensione corrispondente si riferisce allo spessore del materiale in quella dimensione – vale a dire. B – b = spessore totale del materiale parallelo all'asse x.

Oltre ai chiari esempi di peso e utilizzo del materiale, perché le sezioni cave sono spesso descritte come di più efficiente rispetto alle loro controparti solide?

Si consideri una trave soggetta a un carico verticale verso il basso. Ci aspettiamo che le fibre più in alto del materiale subiscano una forza di compressione, mentre le corrispondenti fibre inferiori subiranno una forza di trazione. Le fibre lungo l'asse neutro della sezione (parallela al baricentro della sezione) però, non subirà né compressione né tensione, da qui il nome neutro asse.

È importante, il grandezza di queste forze di compressione o di trazione dipendono dalla distanza da questo asse neutro – al materiale più vicino all'asse neutro deve resistere gsd_rebar_set_example vigore.

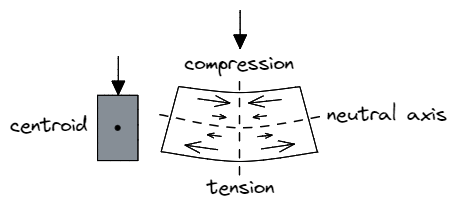
Di conseguenza, il materiale interno di una sezione solida resiste solo a una piccola quantità di forza pur occupando un'ampia area, poiché il materiale più esterno sopporta il carico maggiore! Togliere questa parte interna della sezione e renderla cava migliora di conseguenza la efficienza della sezione per quanto riguarda il suo peso, costo, e uso materiale.

Conclusione

In sintesi, la formula per determinare il momento di inerzia di un rettangolo è Ixx=BD³ ⁄ 12, Iyy=SI³RE ⁄ 12. Per profilati cavi rettangolari, la formula è Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.

Il momento d'inerzia è importante sia per la forza/sollecitazione del momento flettente che per la flessione. Questo è evidente nelle loro formule, come in entrambi i casi, I (Momento d'inerzia) è al denominatore:

fonte: Formula dello stress da flessione

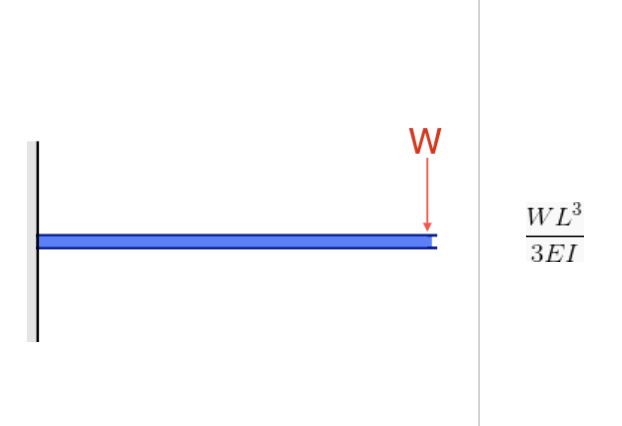
fonte: Equazione della deflessione in una trave a sbalzo

Calcolatore del momento d'inerzia di una circonferenza

Se vuoi saperne di più, dai un'occhiata al nostro tutorial su Momento d’inerzia di un cerchio per vedere come si confrontano le forme di sezione circolare e rettangolare.

Calcolatore gratuito del momento d’inerzia