Disegno a pelo singolo secondo AS 2159 (2009) & 3600 (2018)

In caso di elevato carico laterale o condizioni del suolo sfavorevoli, la fondazione su pali è più preferita rispetto alle fondamenta poco profonde. Tentativi come metodi di modifica del suolo possono essere fatti per evitare cumuli, però, questi metodi possono comportare processi costosi, in cui questo caso, pile forse anche più economiche.

Il modulo SkyCiv Foundation Design include la progettazione di pali conformi all'American Concrete Institute (ACI 318) e standard australiani (COME 2159 & 3600).

Vuoi provare il software Foundation Design di SkyCiv? Il nostro strumento gratuito consente agli utenti di eseguire calcoli di carico senza alcun download o installazione!

Calcolatrice del progetto di fondazione

Progettare la forza geotecnica di un palo

I carichi verticali applicati sui pali sono portati dal supporto di estremità del palo e dalla pelle o dall'attrito dell'albero lungo la sua lunghezza. La forza geotecnica del progetto (R_d,g) è uguale alla massima resistenza geotecnica (R_d,e) moltiplicato per un fattore di riduzione geotecnico (ø_g) come specificato su COME 2159 Sezione 4.3.1.

\({R}_{d,g} = {ø}_{g} × {R}_{d,e}\) (1)

R_d,g = Progettare la forza geotecnica

R_d,e = Massima resistenza geotecnica

ø_g = Fattore di riduzione geotecnico

Massima forza geotecnica (R_d,e)

La resistenza geotecnica finale è uguale alla somma dell'attrito della pelle fattorizzato del pelo (f_m,S ) moltiplicato per l'area della superficie laterale e la resistenza di base moltiplicata per l'area della sezione trasversale sulla punta del palo.

\( {R}_{d,e} = [{R}_{S} × ({f}_{m,S} × {UN}_{S} )] + ({f}_{B} × {UN}_{B} )\) (2)

R_S = Fattore di riduzione per la resistenza dell'albero

f_m,S = Resistenza all'attrito dell'albero

UN_S = Superficie laterale

f_B = Termine di resistenza di base

UN_B = Area della sezione trasversale sulla punta del palo

Per una guida più dettagliata, dai un'occhiata al nostro articolo sul calcolo la resistenza all'attrito della pelle e la capacità portante.

Fattore di riduzione geotecnico (ø_g)

Il fattore di riduzione geotecnico è un calcolo basato sul rischio per il progetto definitivo che tiene conto di diversi fattori, come le condizioni del sito, disegno del mucchio, e fattori di installazione. Il suo valore varia comunemente da 0.40 per 0.90. COME 2159 4.3.1 indica anche come stimare il suo valore come mostrato nell'equazione (3).

\( {ø}_{g} = {ø}_{gb} + [K × ({ø}_{tf} – {ø}_{gb})] ≥ {ø}_{gb} \) (3)

ø_gb = Fattore di riduzione della resistenza geotecnica di base

ø_tf = Fattore di prova intrinseco

K= Fattore di beneficio del test

Il test intrinseco e i fattori di beneficio del test dipendono entrambi dal tipo di test di carico utilizzato sui pali. I loro valori sono specificati nella tabella 1 e sulle equazioni (4) e (5). Il test del carico su pali è discusso brevemente nella Sezione 8 di AS 2159.

Fattore di prova intrinseco (øtf)
Prova di carico statico	0.90
Prove di carico rapide	0.75
Prove di carico dinamico di pali preformati	0.80
Prove di carico dinamico di pali non preformati	0.75
Prova di carico bidirezionale	0.85
Nessun test	0.80

tavolo 1: Valori del fattore di prova intrinseco

Fattore di vantaggio del test per il test di carico statico:

\( K = frac{1.33 × pag}{p + 3.3} ≤ 1\) (4)

Fattore di vantaggio del test per il test di carico dinamico:

\( K = frac{1.13 × pag}{p + 3.3} ≤ 1\) (5)

p = Percentuale del totale delle pile che vengono testate e soddisfano i criteri di accettazione

Il fattore di riduzione della resistenza geotecnica di base viene valutato utilizzando una procedura di valutazione del rischio discussa nella sezione 4.3. di AS 2159. L'esito di tale procedura è l'Individual Risk Rating (IRR) e un disegno complessivo di valutazione media del rischio (ARR) che deve essere utilizzato per determinare il valore di ø_gb come mostrato nella tabella 2.

Fattore di riduzione della forza geotecnica di base (øgb)
Valutazione del rischio medio (ARR)	Categoria di rischio	øgb per sistemi a bassa ridondanza	øgb per sistemi ad alta ridondanza
AR ≤ 1.5	Molto basso	0.67	0.76
1.5 < AR ≤ 2.0	Da molto basso a basso	0.61	0.70
2.0 < AR ≤ 2.5	Basso	0.56	0.64
2.5 < AR ≤ 3.0	Da basso a moderato	0.52	0.60
3.0 < AR ≤ 3.5	Moderare	0.48	0.56
3.5 < AR ≤ 4.0	Da moderato ad alto	0.45	0.53
4.0 < AR ≤ 4.5	Alto	0.42	0.50
ARR > 4.5	Molto alto	0.40	0.47

tavolo 2: Valori per il fattore di riduzione geotecnico di base, (COME 2159 tavolo 4.3.2)

I sistemi a bassa ridondanza sono pile singole pesantemente caricate mentre i sistemi ad alta ridondanza includono grandi gruppi di pile sotto grandi pile o gruppi di pile con più di 4 emorroidi.

Progettare la forza strutturale

Le pile sono strutturalmente progettate quasi come una colonna. Progettare la resistenza strutturale (R_d,S) richiede capacità ultime, come forze assiali e di taglio, e momento flettente. La resistenza strutturale di progetto di un palo di cemento è equivalente alla resistenza di progetto finale (R_noi) ridotto di un fattore di riduzione della forza (ø_S) e un fattore di posizionamento concreto (K), come dichiarato dalla Sezione 5.2.1 di AS 2159.

\( {R}_{d,S} = {ø}_{S} × k × {R}_{noi} \) (6)

ø_S = Fattore di riduzione della forza

k = Fattore di posa del calcestruzzo

R_noi = Massima forza progettuale

I valori per il fattore di riduzione della resistenza sono riportati in tabella 3. Il fattore di posizionamento concreto varia da 0.75 per 1.0, a seconda del metodo di costruzione della pila. però, per pali diversi da calcestruzzo e boiacca, k deve essere preso come 1.0.

Fattori di riduzione della forza (ø)
Forza assiale senza flessione	0.65
Flessione senza forza assiale (øpb)	0.65 ≤ 1.24 – [(13 × kuo)/12] ≤ 0.85
Piegatura con compressione assiale:
(io) Nu ≥ Nub	0.60
(ii) Nu < Nub	0.60 + {(øpb – 0.66) × [1 – (Nu/Nub)]}
cesoia	0.70

tavolo 3: Fattori di riduzione della forza (tavolo 2.2.2, COME 3600-18)

Capacità assiali e flessionali di un unico palo

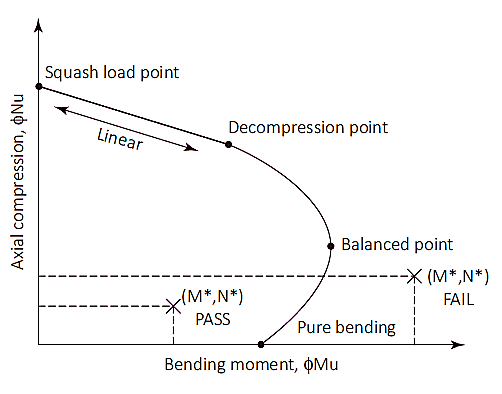
Simile alle colonne, i pali possono anche essere soggetti a compressione combinata e carico flettente. Le capacità assiali e flessionali vengono verificate mediante un diagramma di interazione. Questo diagramma è una rappresentazione visiva del comportamento delle capacità flessionali e assiali causate da un aumento del carico dal punto di flessione puro fino al raggiungimento di un punto di equilibrio.

 

figura 1: Diagramma di interazione delle colonne

Carico di zucca (N_uo)

Il punto di carico dello squash è un punto del diagramma in cui la pila si romperà in pura compressione. A questo punto, il carico assiale viene applicato sul baricentro plastico della sezione per rimanere in compressione senza piegarsi. Carico di zucca (N_uo) e la posizione del baricentro plastico (d_q) sono calcolati come mostrato nelle equazioni (7) & (8). Sebbene la posizione del baricentro di plastica possa essere presa come 1/2 della profondità totale della sezione per sezioni simmetriche con disposizione di armatura simmetrica.

\( {N}_{uo} = ø × [({UN}_{g} – {UN}_{S}) × ({un'}_{1} × f'c) + ({UN}_{S} × {f}_{il suo})] \) (7)

UN_g = Area della sezione trasversale lorda

UN_S = Superficie totale dell'acciaio

un'₁ = 1.0 – (0.003 × f'c) [0.72 ≤α₁ ≤0,85]

f'c = Resistenza del calcestruzzo

f_{il suo} = Resistenza allo snervamento dell'acciaio

\( {d}_{q} = Frac{[(b × D) – {UN}_{S}] × ({un'}_{1} × f'c) × somma_{io=1}^{n} ({UN}_{bi} × {f}_{il suo} × {d}_{fare})}{{N}_{uo}} \) (8)

b = Larghezza della sezione trasversale del palo

D = Profondità o diametro della sezione del palo

UN_bi = Area della barra d'armatura considerata

d_fare = Si considera la profondità della barra d'armatura

Squash punto di carico fino al punto di decompressione

Il punto di decompressione è dove è uguale la deformazione del calcestruzzo alla fibra di compressione estrema 0.003 e la deformazione nella fibra a trazione estrema è zero. La resistenza del palo tra il carico di schiacciamento ed i punti di decompressione può essere calcolata mediante interpolazione lineare con fattore di riduzione della resistenza (ø_S) di 0.6.

Punto di decompressione fino alla pura flessione

Il punto di flessione puro è dove la capacità di carico assiale è zero. Il passaggio dal punto di decompressione alla flessione pura utilizza un fattore di riduzione della forza di 0.6 per 0.8 e un parametro di input (K_u) è introdotto. Il valore di k_u inizia a 1 al punto di decompressione e diminuisce fino a raggiungere la flessione pura. Tra il passaggio dei due punti, si raggiunge una condizione equilibrata. A questo punto, la deformazione del calcestruzzo è al suo limite (e_c=0,003) e la deformazione esterna dell'acciaio raggiunge la resa (e_S=0,0025), Il valore di k_u a questo punto è approssimativamente 0.54 con un fattore di riduzione della forza di 0.6.

Una volta un valore di k_u è selezionato, possono essere calcolate le forze di trazione e di compressione della sezione. Il carico assiale sulla sezione è equivalente alla somma delle forze di trazione e di compressione, mentre il momento flettente viene calcolato risolvendo queste forze attorno all'asse neutro. Di seguito sono elencati i calcoli per le forze di compressione e di trazione

Forza dovuta al cemento (F_cc):

\( {F}_{cc} = {un'}_{2} × f'c × {UN}_{c} \) (9)

un'₂ = 0.85 – (0.0015 × f'c) [un'_{2 ≥}0.67]

UN_c = Area del blocco di compressione (fare riferimento alla figura 2)

= b × c × k_u × d (sezione rettangolare)

=(1/2) × (θ – sinθ) × (D/2)² (sezione circolare)

γ = 0.97 – (0.0025 × f'c) [c _≥0.67]

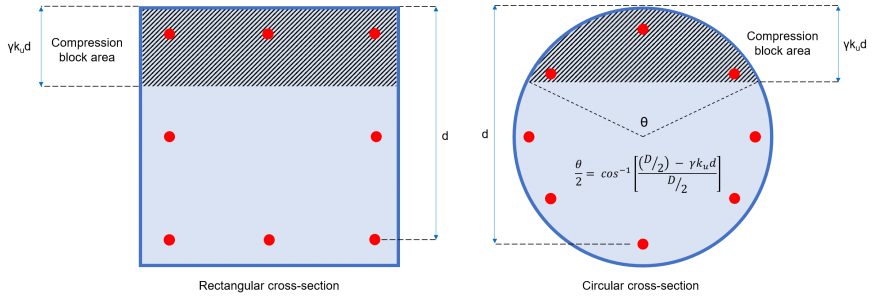
figura 2: Area del blocco di compressione del calcestruzzo

Forza (F_e) e momento (M_io) contributo di ogni singolo bar:

Ciascuna barra d'armatura della sezione esercita una forza che può essere di compressione o di trazione, a seconda della deformazione della barra del valore (e_e) mostrato nell'equazione (10).

\( {e}_{e} = frac{{e}_{c}}{({K}_{u} × d)} × [({K}_{u} × d) – {d}_{fare}] \) (10)

d_fare = Profondità della barra considerata

e_c= Deformazione del calcestruzzo = 0.003

Se e_e < 0 (la barra è in tensione)

Se e_e > 0 (la barra è in compressione)

Barra in compressione:

\( {F}_{e} = {σ}_{e} × {UN}_{bi} \) (11)

σ_e = Sollecitazione in barra = Minimo [(e_e × E_S ), f_{il suo}]

E_S = Modulo elastico dell'acciaio

UN_bi = Zona bar

Barra in tensione:

\( {F}_{e} = [{σ}_{e} – ({un'}_{2} × f'c)] × {UN}_{bi} ≥ 0\) (12)

σ_e = Sollecitazione in barra = Minimo [(e_e × E_S ), –f_{il suo}]

E_S = Modulo elastico dell'acciaio

UN_bi = Zona bar

Momento per ogni barra:

\( {M}_{io} = {F}_{e} × {d}_{fare} \) (13)

Portata assiale del palo:

\( {l'isola}_{u} = ø × [ {F}_{cc} + {Σ}_{io=1}^{n} {F}_{e}]\) (14)

Capacità flessionale del palo:

\( {dolorante}_{u} = ø × [ ({N}_{u} × {d}_{q}) – ({F}_{cc} × {e}_{c}) – {Σ}_{io=1}^{n} {M}_{io}] \) (15)

Momento flettente di progetto:

Sezione 7.2 specifica che le pile devono avere una tolleranza di fuori posizione di 75 mm per il posizionamento orizzontale delle pile. Questo requisito può indurre un momento flettente pari al carico assiale moltiplicato per l'eccentricità di 75 mm. Inoltre, deve essere considerato anche un momento minimo di progetto equivalente alla forza assiale moltiplicata per 5% della larghezza minima complessiva della pila. Perciò, il momento flettente di progetto dovrebbe essere il valore maggiore tra le equazioni 16a e 16b.

\( {M}_{d} = {{M}^{*}}_{applicato} + ({N}^{*} × 0.075 m) \) (16un')

\( {M}_{d} = {N}^{*} × (0.05 Un palo di cemento lungo 12 metri con un diametro di) \) (16B)

M_d = Momento flettente di progetto

M*_applicato = Momento applicato

N* = Carico assiale

D = Larghezza pila

Capacità di taglio di un singolo palo

Il calcolo della resistenza al taglio deve essere conforme alla Sezione 8.2 di AS 3600. La resistenza al taglio è equivalente a una capacità di taglio combinata del calcestruzzo e dell'armatura in acciaio (equazione 17).

\( {øV}_{u} = ø × ({V }_{uc} + {V }_{noi}) ≤ {øV}_{u,max} \) (17)

Resistenza al taglio del calcestruzzo (V _uc)

Il contributo del calcestruzzo alla capacità di taglio viene calcolato come mostrato nell'equazione (18) che è definito nella sezione 8.2.4.1 di AS 3600. Questa sezione richiede anche che il valore di √f'c non debba essere superiore 9.0 MPa. I valori per il parametro k_v e θ_v sono determinati utilizzando un metodo semplificato suggerito dall'art 8.2.4.3 di AS 3600.

\( {V }_{uc} = {K}_{v} × b × {d}_{v} × sqrt{f'c} \) (18)

d_v = Profondità di taglio effettiva = Le sezioni rastremate sono attualmente supportate nei seguenti tipi di sezione [(0.72 Un palo di cemento lungo 12 metri con un diametro di ), (0.90 × d )]

Determinazione dell'area minima dell'armatura a taglio (UN_sv.min) & K_v:

L'area dell'armatura a taglio (UN_sv) è l'area totale della barra di tutte le barre d'acciaio fornite legate nella stessa direzione del carico applicato. Sezione 8.2.1.7 di AS 3600 fornito l'equazione per le armature a taglio trasversale minimo, che sarà:

\( \frac{{UN}_{sv.min}}{S} = frac{0.08 × sqrt{f'c} × b}{{f}_{e f}} \)

f_{e f} = Resistenza allo snervamento delle barre d'armatura a taglio

s= Spaziatura da centro a centro delle barre d'armatura a taglio

Per (UN_sv/S) < (UN_sv.min/S):

\( {K}_{v} = frac{200}{[1000 + (1.3 × {d}_{v} )]} ≤ 0.10\)

Per (UN_sv/S) ≥ (UN_sv.min/S):

\( {K}_{v} = 0.15 \)

Resistenza al taglio delle barre d'acciaio (V _noi)

Il contributo delle armature a taglio trasversale alla capacità di taglio calcolata è mostrato nell'equazione (19), che è definito nella Sezione 8.2.5 di AS 3600.

\( {V }_{noi} = frac{{UN}_{sv} × {f}_{e f} × {d}_{v}}{S} × lettino{θ}_{v} \) (19)

θ_v= angolo di inclinazione del puntone di compressione = 36º

Massima resistenza al taglio (V _u.max)

La capacità di taglio è limitata e in nessun caso deve superare il valore massimo specificato nella Sezione 8.2.6 di AS 3600 (equazione 20).

\( {V }_{u.max} = 0.55 × [ (f'c × b × {d}_{v}) × frac{culla{θ}_{v} + culla{un'}_{v}}{1 + lettino^{2}{θ}_{v} }] \) (20)

un'_v= angolo tra l'armatura a taglio inclinato e l'armatura a trazione longitudinale≈ 90º

Massima resistenza al taglio (V _u)

La resistenza al taglio totale apportata dal calcestruzzo e dalle armature a taglio deve essere inferiore o uguale al valore limite di V_u.max

\( {V }_{u} = ({V }_{uc} + {V }_{noi} ) ≤ {V }_{u.max} \) (21)

Resistenza al taglio di progetto (øV_u)

Il fattore di riduzione della capacità che deve essere applicato per la resistenza a taglio ultima è ø = 0.7. Perciò, la resistenza al taglio di progetto del palo è data da:

\( {øV}_{u} = ø × ({V }_{uc} + {V }_{noi} ) \) (22)

Riferimenti

• Pacchetto, Lonnie (2018). Guida australiana per ingegneri strutturali. CRC Press.
• Progettazione e installazione di palificazioni (2009). COME 2159. Standard australiano
• Strutture in cemento (2018). COME 3600. Standard australiano