Tabella dei contenuti
- Tipi di supporti e loro reazioni
- Una guida passo passo sulla determinazione delle reazioni di supporto nelle travi
- Software SkyCiv Beam
Tipi di supporti e loro reazioni
In questo articolo, discutiamo della formula della forza di reazione e di come trovare le reazioni di supporto. Primo, è importante comprendere anche i diversi tipi di supporti e quali reazioni producono nel tuo modello di analisi, compresi i momenti di reazione. Di seguito è riportato un breve cheat sheet dei diversi tipi di supporto e delle loro reazioni:
| Tipo di supporto | Traduzione | Rotazione | Appunti |
|---|---|---|---|
Supporto fisso |
Fisso in tutte le direzioni Reazioni in X,E,Z |
Fisso in tutte le direzioni Reazioni in X,E,Z |
FFFFFF – Reazioni in tutti i gradi di libertà |
Supporto rullo orizzontale |
Risolto in Y Reazioni solo in direzione Y |
Rilasciato in tutte le direzioni Nessuna reazione rotazionale |
RFFRRR – Le reazioni sono solo nella direzione Y |
Supporto appuntato o incernierato |
Risolto in X,E,Z Reazioni in X,E,Z |
Rilasciato in tutte le direzioni Nessuna reazione rotazionale |
FFFRRR – Reazioni in tutte le traduzioni, nessuno in rotazione |
| Supporto a sbalzo |
Fisso in tutte le direzioni Reazioni in X,E,Z |
Fisso in tutte le direzioni Reazioni in X,E,Z |
Uguale a fisso |
Una guida passo passo sulla determinazione delle reazioni di supporto nelle travi:
Una guida passo passo per determinare le reazioni di supporto nelle travi, ed è generalmente il più semplice. Implica il calcolo sia della formula della forza di reazione che dei momenti di reazione sui supporti (supporta A e B nell'esempio seguente) a causa delle forze che agiscono sulla trave. La formula della forza di reazione viene utilizzata per trovare le forze esercitate sugli appoggi a causa dei carichi agenti sulla trave. Inoltre, è fondamentale comprendere i momenti di reazione ai supporti fissi per risolvere il problema. Avrai bisogno di sapere questo per progredire e calcolare diagrammi del momento flettente (BMD) e diagrammi delle forze di taglio (SFD); una parte importante dei tuoi corsi di statica e strutturale / universitario. SkyCiv offre un potente Calcolatore di reazione gratuito che ti consente di modellare qualsiasi raggio e mostrare questi calcoli manuali per te, ma è anche un concetto importante da capire.
Tutorial video: Determina le reazioni ai supporti
Quando risolviamo un problema come questo, vogliamo prima ricordare che il raggio è statico; il che significa che non si sta muovendo. Dalla semplice fisica, questo significa che la somma delle forze nella direzione y è uguale a zero (vale a dire. le forze totali verso il basso sono uguali alle forze totali verso l'alto). Una seconda formula da ricordare è che la somma dei momenti su un dato punto è uguale a zero. Questo perché il raggio è statico e quindi non rotante.
Per determinare le reazioni ai supporti, segui questi semplici passaggi:
1. Somma di momenti (ΣM = 0)
Tutto ciò che dobbiamo sapere sui momenti in questa fase è che sono uguali alla forza moltiplicata per la distanza da un punto (vale a dire. la forza x distanza da un punto). Si consideri un semplice esempio di una trave di 4 m con un supporto a perno in A e supporto a rulli in B. Il diagramma del corpo libero è mostrato sotto dove Ay e By sono le reazioni verticali ai supporti: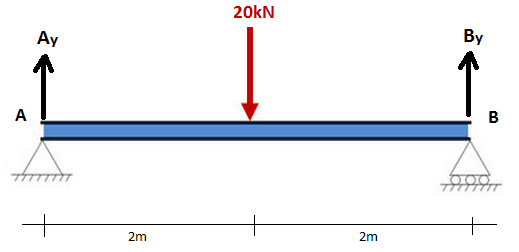
Per prima cosa vogliamo considerare la somma dei momenti attorno al punto B e lasciare che sia uguale a zero. Abbiamo scelto il punto B per dimostrare che ciò può essere fatto a entrambe le estremità della trave (a condizione che sia supportato da pin). Tuttavia, potresti lavorare altrettanto facilmente dal punto A. Quindi, ora sommiamo i momenti attorno al punto B e lasciamo che la somma sia uguale 0:
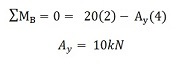
NOTA: La convenzione del segno che abbiamo scelto è che i momenti in senso antiorario sono positivi e i momenti in senso orario sono negativi. Questa è la convenzione sui segni più comune, ma dipende da te. È necessario utilizzare SEMPRE la stessa convenzione sui segni durante l'intero problema. Usa sempre la stessa convenzione sui segni dall'inizio. Ora abbiamo la nostra prima equazione. Dobbiamo risolvere un'altra equazione per trovare By (la forza di reazione verticale al supporto B).
2. Somma delle forze orizzontali (ΣFy = 0)
Somma le forze in y (verticale) direzione e lascia che la somma sia uguale a zero. Ricordarsi di includere tutte le forze comprese le reazioni e i carichi normali come i carichi puntuali. Quindi, se sommiamo le forze nella direzione y per l'esempio precedente, otteniamo la seguente equazione:
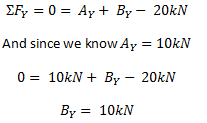
NOTA: Ancora una volta ci siamo attenuti a una convenzione sui segni che doveva prendere le forze al rialzo (le nostre reazioni) come forze positive e discendenti (il carico puntuale) come negativo. Ricorda che la convenzione sui segni dipende da te, ma devi SEMPRE utilizzare la stessa convenzione sui segni durante l'intero problema.
Quindi ce l'abbiamo, abbiamo usato le due equazioni precedenti (la somma dei momenti è uguale a zero e la somma delle forze verticali è uguale a zero) e ha calcolato che la reazione al supporto A è 10 kN e la reazione al supporto B 10kN. Questo ha senso in quanto il carico puntuale si trova proprio al centro della trave, il che significa che entrambi i supporti dovrebbero avere le stesse forze verticali (vale a dire. è simmetrico).
Quando si calcolano le reazioni vincolari, vengono utilizzate sia la somma delle forze che la somma dei momenti. La formula della forza di reazione aiuta a calcolare le forze verticali e orizzontali, mentre la somma dei momenti di reazione consente di garantire che la trave rimanga in equilibrio statico.
In sintesi, ecco il completo calcoli a mano prodotto da SkyCiv Beam:
Software SkyCiv Beam
Attraverso questo articolo, hai imparato il concetto di forze di reazione ai supporti e come calcolare le reazioni dei supporti. Software di analisi del raggio SkyCiv consente agli utenti di analizzare le strutture delle travi in modo semplice e accurato. È possibile ottenere un'analisi del membro della trave, comprese le reazioni, forza di taglio, momento flettente, la deflessione , sottolinea, e Come rivedere passo dopo passo il calcolo delle reazioni in pochi secondi.
Se vuoi provalo prima, Calcolatore gratuito di travi è un ottimo modo per iniziare, o semplicemente registrati gratuitamente oggi!
