La fondazione è un elemento essenziale di una struttura per fornire stabilità complessiva trasmettendo e distribuendo i carichi totali della struttura al suolo. Fondamenti poco profondi, come basi rettangolari o quadrate isolate, sono il tipo di fondazione preferito per la semplicità della loro costruzione e il costo complessivo rispetto alle fondazioni profonde. La stima della pressione alla base influisce notevolmente sulla progettazione e sul dimensionamento del basamento. Tipicamente, il rapporto di utilità tra la capacità portante ammissibile del terreno e la pressione di base regolante sotto il plinto è la base della dimensione iniziale del plinto. Una volta impostate le dimensioni iniziali della fondazione, ulteriori controlli di progettazione per la sicurezza e la stabilità, come il taglio unidirezionale e bidirezionale, capacità di flessione, e controlli sulla lunghezza dello sviluppo, vengono controllati a seconda del codice di progettazione utilizzato.

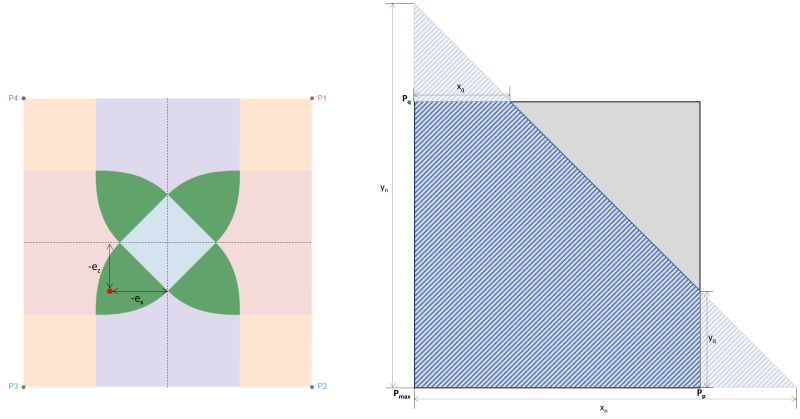
Quando un basamento è soggetto a flessione biassiale (M_x, M_z), si presume che il carico assiale (P) agisce su una coordinata di eccentricità (e_x, e_z) dove c'è una tendenza a ruotare dal centro. L'interazione tra terreno e fondazione dipende principalmente dalla dimensione della fondazione e dalla risultante eccentricità dei carichi applicati. A seconda della posizione dell'eccentricità risultante, la pressione di base fa sì che il plinto sia in piena o parziale compressione. In pratica, si consiglia di progettare un basamento in piena compressione. La compressione parziale o la perdita di contatto tra il suolo e il basamento non devono essere trascurate, ma la maggior parte dei progettisti evita questo scenario a causa della sua complessità di calcolo. La fondazione è in piena compressione quando l'eccentricità risultante si trova all'interno del kern o sotto la Zona C. L'eccentricità al di fuori della Zona C mette la base in parziale compressione. figura 1 mostra le diverse zone designate su base rettangolare.

Questo articolo si concentrerà sul calcolo delle pressioni d'angolo in diverse classificazioni di zona basate su Bellos & Traccia (2017) e SS. di Ray (1995) studi.

Classificazioni di zona a base rettangolare

Le classificazioni delle zone di un plinto rettangolare derivano da più studi di diversi autori per sviluppare un approccio pratico alla stima della distribuzione della pressione del suolo nelle condizioni di carico previste. Come mostrato in figura 1, ci sono cinque diverse regioni (Zone A-E) a seconda della posizione dell'eccentricità risultante. Ad ogni zona corrisponde un carico diverso, distribuzione della pressione di base, e deformazione. Zona C, noto anche come il kern, è il nucleo principale. È la regione ideale per progettare un basamento, con conseguente compressione completa sul basamento. Le dimensioni di questa regione sono equivalenti a 1/6 della rispettiva lunghezza di appoggio.

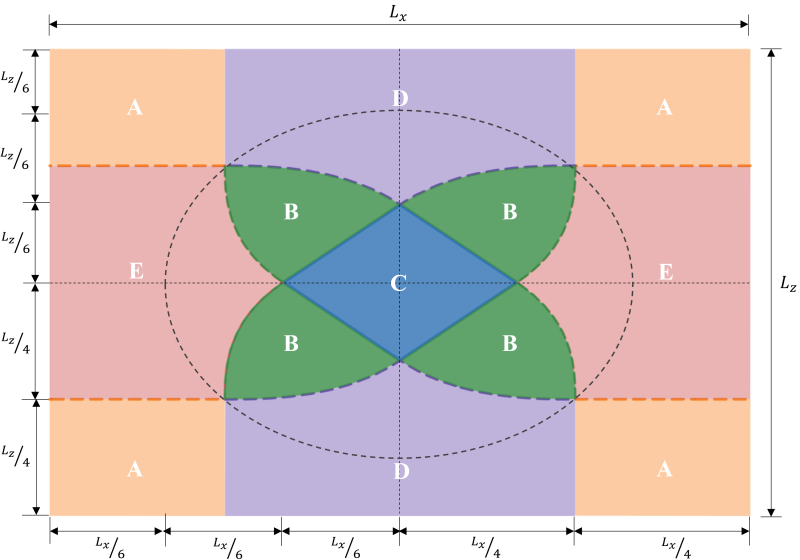
figura 1: Classificazioni di zona a base rettangolare

 

Il nucleo secondario è l'area ellittica (delimitato dalla linea tratteggiata in figura 1) con i suoi semiassi maggiore e minore uguali a 1/3 della rispettiva lunghezza di appoggio. Questa regione copre l'intera zona B & C e alcune parti delle zone D & E. Il nucleo secondario provoca una parziale compressione della fondazione. È buona norma mantenere l'eccentricità all'interno della zona secondaria per un progetto di fondazione accettabile.

L'eccentricità oltre la zona secondaria è il risultato di un elevato carico biassiale. Copre l'intera zona A e le restanti parti delle zone D & E. Si raccomanda di evitare di progettare il basamento in queste regioni in quanto si corre il rischio di ribaltamento. Quindi, si consiglia di ridisegnare le dimensioni del basamento per questo tipo di carico.

 

Di seguito vengono elencate le formule analitiche per la risoluzione delle pressioni agli angoli in ciascuna classificazione di zona.

Zona C (Nucleo principale, Zona di compressione completa)

Come accennato, questo è il caso più preferito per la progettazione di fondazioni poiché è in grado di mettere in compressione l'intera base della fondazione, come mostrato in figura 2. Questo caso è rappresentato da una piccola eccentricità all'interno del kern o da nessuna eccentricità. figura 2 mostra l'eccentricità all'interno del kern con la sua massima pressione agli angoli P3 & P4 e minima pressione agli angoli P1 & P2.

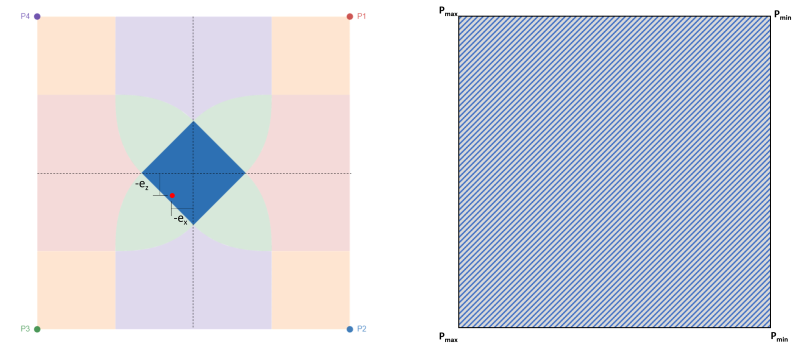
figura 2: Eccentricità (-e_x, -e_z) in Zona C & area di compressione completa

Le sezioni rastremate sono attualmente supportate nei seguenti tipi di sezione & minime pressioni d'angolo (Bellissimo & Traccia, 2017):

 

 

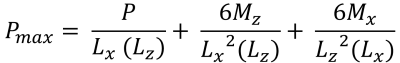
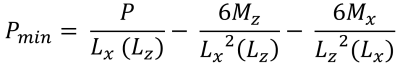
Pressioni d'angolo basate sull'eccentricità
	P1	P2	P3	P4
+ex, +ez	Pmax	Pmax	Pmin	Pmin
+ex, -ez	Pmax	Pmax	Pmin	Pmin
-ex, -ez	Pmin	Pmin	Pmax	Pmax
-ex, +ez	Pmin	Pmin	Pmax	Pmax

Zona A (Zona di compressione triangolare)

Questo caso corrisponde a quattro aree rettangolari in ogni angolo del basamento. Di solito si verifica con una grande eccentricità biassiale, imponendo un'alta area di compressione triangolare in uno degli angoli, come mostrato dalla regione ombreggiata in figura 3. Gli angoli rimanenti perdono il contatto con il suolo. Quindi, questo caso non è consigliabile per il design.

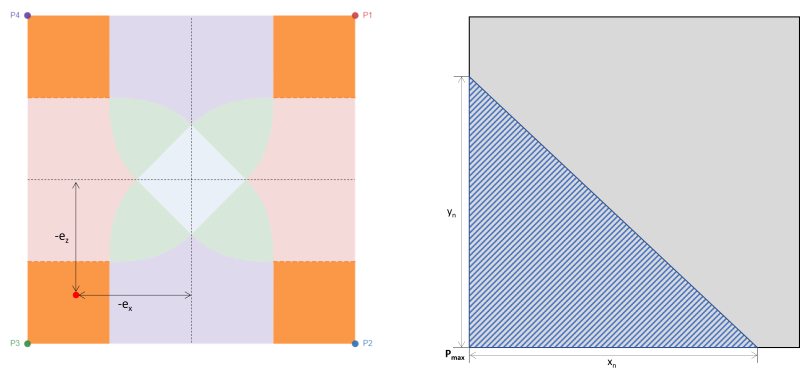figura 3: Eccentricità (-e_x, -e_z) alla Zona A & area di compressione triangolare attorno a P3

 

Pressione massima (Bellissimo & Traccia, 2017):

 

 

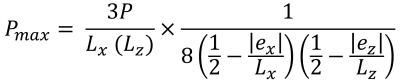
Pressioni d'angolo basate sull'eccentricità
	P1	P2	P3	P4
ex(+), ez(+)	Pmax	0	0	0
ex(+), ez(-)	0	Pmax	0	0
ex(-), ez(-)	0	0	Pmax	0
ex(-), ez(+)	0	0	0	Pmax

Zona D (Zona di compressione trapezoidale)

La zona D corrisponde anche a grandi eccentricità nelle aree attaccate nella direzione x del basamento, come mostrato in figura 4. L'eccentricità nella direzione z (e_z) è molto maggiore che nella direzione x (e_x). In questo caso, due angoli del basamento perdono il contatto con il suolo e producono un'area di compressione trapezoidale. Rispetto alla zona A, che è interamente al di fuori della zona secondaria, una porzione della zona D è ancora coperta dalla zona secondaria.

 

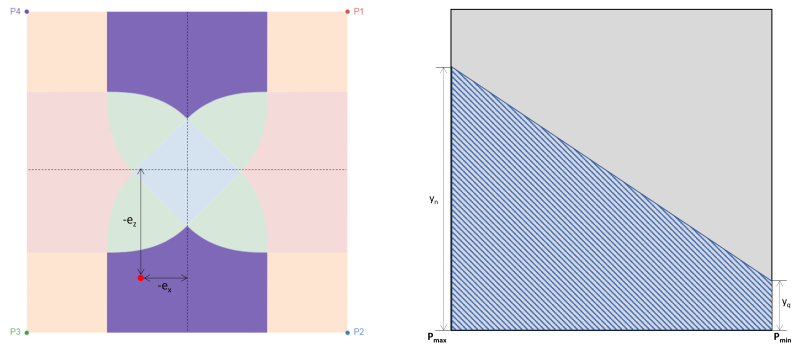
figura 4: Eccentricità (-e_x, -e_z) in Zona D & area di compressione trapezoidale attorno a P3

 

Le sezioni rastremate sono attualmente supportate nei seguenti tipi di sezione & minime pressioni d'angolo (Bellissimo & Traccia, 2017):

 

 

 

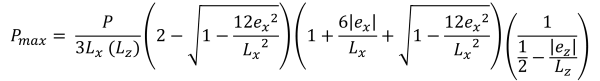
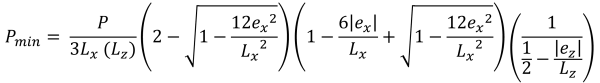
Altezze verticali dell'area di compressione trapezoidale (Bellissimo & Traccia, 2017):

 

 

 

 

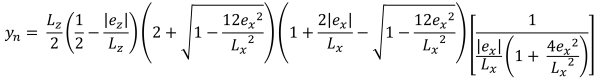
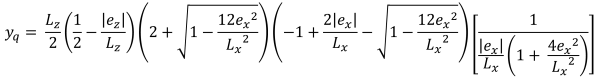
Pressioni d'angolo basate sull'eccentricità
	P1	P2	P3	P4
ex(+), ez(+)	Pmax	0	0	Pmin
ex(+), ez(-)	0	Pmax	Pmin	0
ex(-), ez(-)	0	Pmin	Pmax	0
ex(-), ez(+)	Pmin	0	0	Pmax

 

Zone E (Zona di compressione trapezoidale)

Simile alla zona D, anche questo caso produce un'area di compressione trapezoidale ma è causata da una grande eccentricità nella direzione x(e_x).

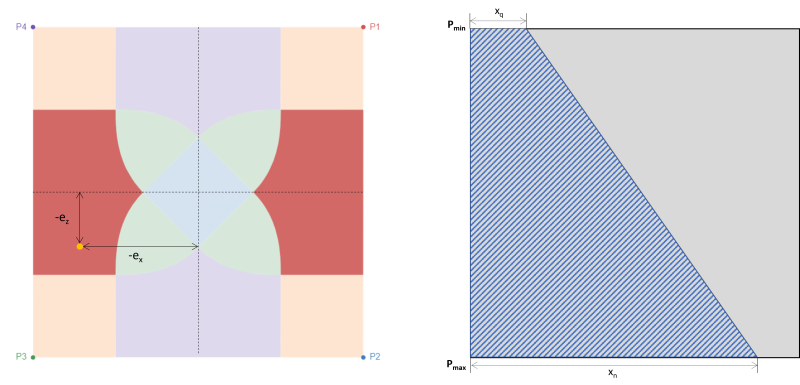figura 5: Eccentricità (-e_x, -e_z) in Zona E & area di compressione trapezoidale attorno a P3

 

Le sezioni rastremate sono attualmente supportate nei seguenti tipi di sezione & minime pressioni d'angolo (Bellissimo & Traccia, 2017):

 

 

 

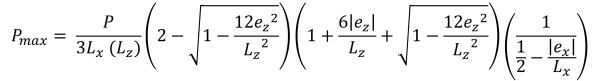
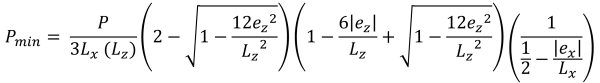
Basi orizzontali dell'area di compressione trapezoidale (Bellissimo & Traccia, 2017):

 

 

 

 

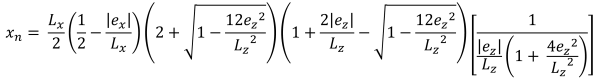
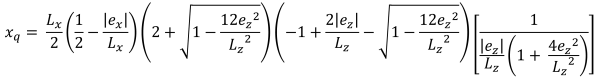
Pressioni d'angolo basate sull'eccentricità
	P1	P2	P3	P4
ex(+), ez(+)	Pmax	Pmin	0	0
ex(+), ez(-)	Pmin	Pmax	0	0
ex(-), ez(-)	0	0	Pmax	Pmin
ex(-), ez(+)	0	0	Pmin	Pmax

Zona B (Zona di compressione pentagonale)

Questo caso si verifica quando i carichi applicati sui plinti generano una moderata eccentricità all'interno della zona secondaria. Le aree coperte dalla zona B sono delimitate da due lati curvi e da una base piatta attorno agli esterni della zona C. In questo caso, viene prodotta un'area di compressione pentagonale, e solo un angolo del basamento perde il contatto con il suolo. Tuttavia, le soluzioni fornite di seguito sono leggermente complesse e richiedono metodi di risoluzione numerica per le pressioni d'angolo e la x & y intercettazioni dell'area di compressione.

Pressioni d'angolo (Bellissimo & Traccia, 2017):

 

 

 

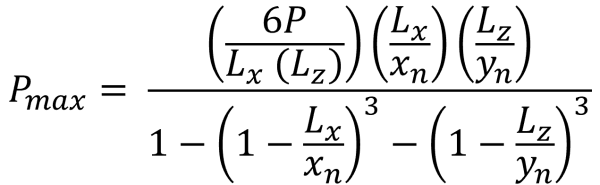
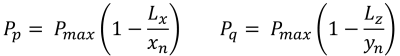
Lati pentagonali dell'area di compressione (Bellissimo & Traccia, 2017):

 

 

 

 

 

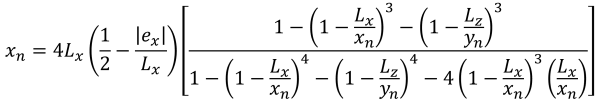
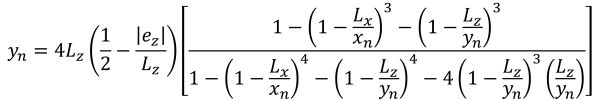
Pressioni d'angolo basate sull'eccentricità
	P1	P2	P3	P4
ex(+), ez(+)	Pmax	Pq	0	Pp
ex(+), ez(-)	Pp	Pmax	Pq	0
ex(-), ez(-)	0	Pp	Pmax	Pq
ex(-), ez(+)	Pq	0	Pp	Pmax

 

In alternativa, una soluzione più diretta di S.S. Ray (1995) può essere utilizzato per le pressioni d'angolo e le intercettazioni della zona di compressione pentagonale. Le equazioni sono riportate di seguito:

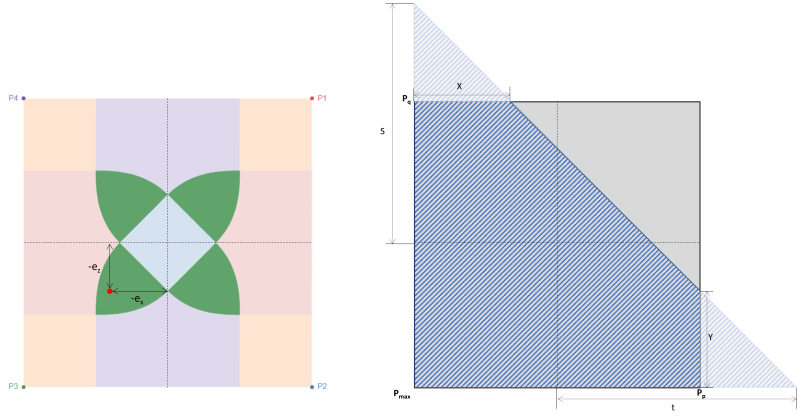
Pressioni d'angolo (SS. Ray, 1995):

 

 

 

 

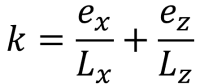
Lati pentagonali dell'area di compressione (SS. Ray, 1995):

 

 

---

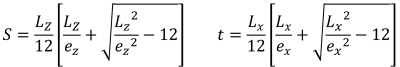
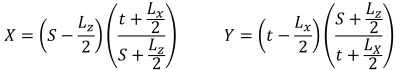
SkyCiv di Modulo di progettazione della fondazione è in grado di risolvere le pressioni alla base di un plinto rettangolare in calcestruzzo. Ulteriori controlli di progettazione in conformità con diversi codici di progettazione (ACI 318-14, Norma australiana 2009 & 2018, Eurocodice, e gli standard canadesi) sono anche disponibili.

Ultimo aggiornamento

L'ultima versione del modulo Foundation è ora integrata con l'analisi degli elementi finiti (BRUTTA), che offre un'analisi della pressione del suolo più potente e introduce l'analisi del braccio di legno da utilizzare per un controllo a flessione molto più dettagliato. I risultati FEA per la pressione del suolo e i momenti del braccio armato del legno possono essere visualizzati in 3D e sono stati aggiunti ai rapporti.

 

Vuoi provare il software Foundation Design di SkyCiv? Il nostro strumento gratuito consente agli utenti di esibirsi calcoli del basamento in calcestruzzo senza alcun download o installazione!

Calcolatore gratuito di fondazione in calcestruzzo

Riferimenti:

• Bellissimo, J., Traccia, N. (2017). Soluzione analitica completa per la distribuzione lineare della pressione del suolo sotto un basamento rigido rettangolare diffuso.
• Completamente sommerso, Completamente sommerso. (2007). Completamente sommerso (7th Edizione). Completamente sommerso
• Rawat, S., e. al. (2020). Basamenti rettangolari isolati sotto flessione biassiale: Una valutazione critica e una metodologia di analisi semplificata.
• Ray, SS. (1995). Cemento armato. Scienza Blackwell