Come calcolare le forze assiali di un sistema di travatura reticolare utilizzando il metodo dei giunti?
In questo tutorial, spiegheremo come utilizzare il metodo dei giunti per calcolare le forze degli elementi interni in un sistema o struttura a traliccio.
Queste forze sono note come forze assiali e sono molto importanti nell'analisi della travatura reticolare. Se non sei chiaro su cosa sia visto un traliccio nel nostro articolo – Che cos'è una capriata. Il metodo delle articolazioni consiste fondamentalmente nell'osservare ciascuna delle "articolazioni"’ (dove i membri si incontrano) e applicando equazioni statiche per risolvere.
La cosa grandiosa è, Aggiungi Supporti illimitati con il pieno controllo sui loro codici di ritenuta lo fa automaticamente per te. Modella i tuoi tralicci e il software mostrerà l'elaborazione interattiva passo dopo passo del metodo dei giunti!

Step 1: Calcola le reazioni ai supporti
Primo, calcoliamo il reazioni agli appoggi. Inizieremo esaminando un semplice esempio di a 5 sistema di travatura reticolare:
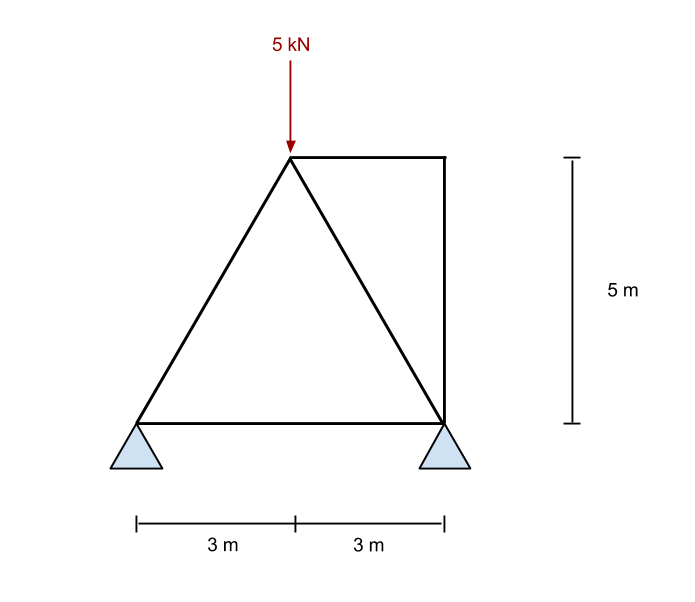
Per calcolare il momento flettente in questo sistema a traliccio, per prima cosa consideriamo zero la somma dei momenti alla reazione sinistra. Lo facciamo ignorando tutti i membri e osservando solo le forze e i supporti nella struttura. Questo è lo stesso del metodo utilizzato nelle reazioni del momento flettente nel nostro precedente tutorial.
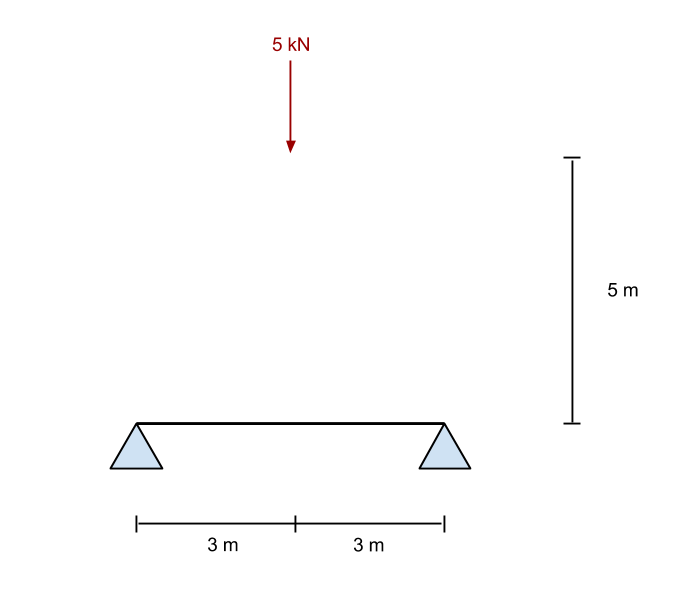
Dalle equazioni precedenti, risolviamo per la forza di reazione al punto B (il giusto supporto). Nel nostro esempio, questo funziona per essere 2.5 kN verso l'alto. Adesso, se prendiamo la somma delle forze in y (verticale) direzione, troviamo quel supporto A (il supporto sinistro) è anche dato come 2.5 kN.
Step 2: Considera uno dei supporti:
Ora che abbiamo le forze di reazione possiamo iniziare l'analisi del resto di questa struttura reticolare. in primo luogo, guardiamo a una delle nostre forze conosciute – in questo caso, considereremo la reazione del supporto sinistro di +2.5 kN. Poiché sappiamo che questa forza si verifica a questo punto, considereremo solo questo punto isolatamente. Ripetiamo questo processo più volte, quindi è importante esercitarsi e apprendere il processo al fine di avere una buona conoscenza di come risolvere le forze assiali nelle strutture reticolari. Quindi di nuovo, considera il primo punto al supporto:
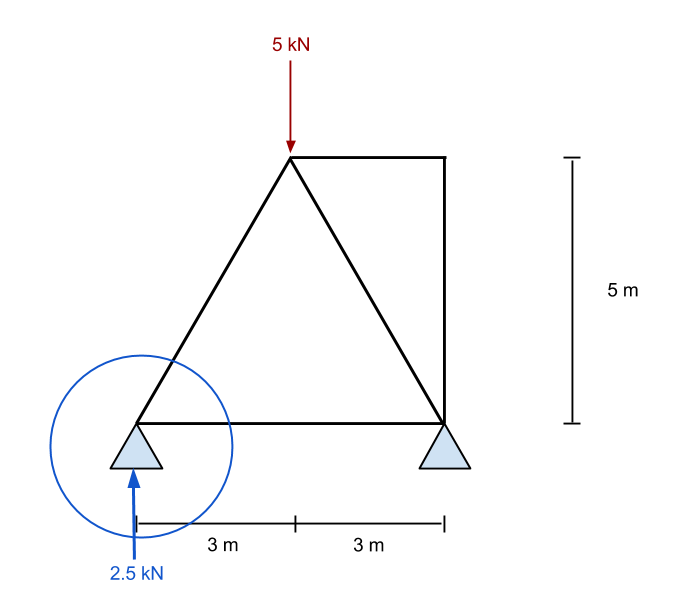
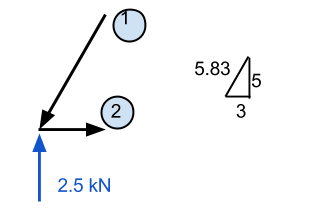
Ingrandendo questo punto, vediamo tutte le forze conosciute che agiscono su questo punto. Dalla statica, sappiamo che le forze nelle direzioni x e y devono entrambe sommarsi a zero. Di conseguenza, se sappiamo che c'è una forza verticale ascendente, allora ci deve essere una forza verso il basso per contrastarlo. Poiché abbiamo già il valore di una forza rivolta verso l'alto, quindi proveremo a valutare il numero di membro 1 primo.
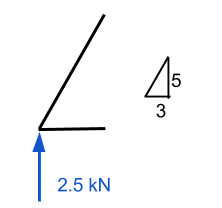
Qui è necessaria una certa conoscenza dei vettori. È importante ricordare che tutte le forze devono sommarsi a zero per entrambe le direzioni x e y. Nel nostro esempio, la distanza orizzontale è di 3 m mentre quella verticale è di 5 m – lasciandoci con l'ipotenusa pari a circa 5.83 m. Usando questo, possiamo dedurre che la normale componente di forza del membro 1 è uguale a (5.83)/(5) volte la forza verticale di 2.5 kN. Ciò equivale a 2.92 kN e DEVE essere una forza che agisce verso il basso se il punto deve rimanere fermo.
Membro 2 può essere calcolato più o meno allo stesso modo. Se conosciamo quel membro 1 sta agendo verso il basso, poi sappiamo che deve agire anche a sinistra. Di conseguenza, sappiamo membro 2 deve generare una forza che tira il punto verso destra per mantenere le forze nella direzione x. Questo valore viene calcolato da (3/5.83) x 2.92 kN ed è uguale a 1.51 kN.
Step 3: Spostati in un altro punto:
Dopo aver calcolato le forze interne del primo membro nel nostro traliccio, ora guarderemo a un altro punto per ripetere il processo:
Ancora una volta, ingrandiremo il punto di riferimento e considereremo tutte le forze note che agiscono sul punto:
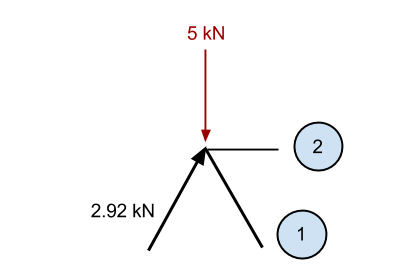
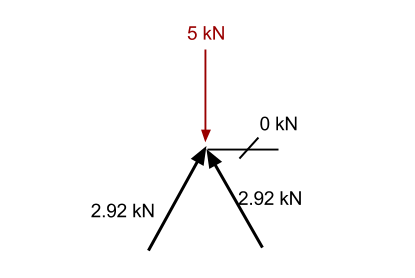
Più o meno allo stesso modo di prima, se sommiamo la componente verticale nota di 2.92 membro kN (2.5 kN in direzione verticale) che per il – 5kN forza verso il basso, allora abbiamo un eccesso nella direzione verso il basso di 2.5 kN (5 – 2.5). Di conseguenza, conosciamo quel membro 1 deve provocare una forza verso l'alto per mantenere il punto statico. Questa forza deve avere una componente verticale di 2.5 kN, e poiché è allo stesso angolo del membro precedente, allora deve essere anche la forza assiale interna 2.92 kN.
Consideriamo ora le forze nella direzione x. A questo punto, tutta la forza verticale dal membro 1 sta resistendo alla forza verticale dell'elemento calcolato in precedenza. Ciò significa che la somma delle forze nella direzione x è già zero. Di conseguenza, non ci può essere forza in membro 2 oppure il punto diventerà sbilanciato e non più statico.
Step 4: Spostati in un altro punto:
Guardando a questo punto, possiamo vedere che c'è un caso speciale. In questa situazione, qualsiasi forza che spinge verso l'alto non avrà alcuna azione di resistenza possibile, poiché non vi è alcun altro elemento in grado di fornire una forza verso il basso per mantenere il punto statico. Di conseguenza, poiché la somma delle forze deve essere zero, a quel membro non può essere associata alcuna forza. It, perciò, non ha forza ed è noto come Zero Member.
Ancora una volta, se guardiamo alla somma delle forze nella direzione x, possiamo vedere che c'è solo un membro che ha una forza nella direzione x. Di conseguenza, anche questo deve avere 0 forza assiale in modo che la somma delle forze sia uguale a zero.

Soluzione finale
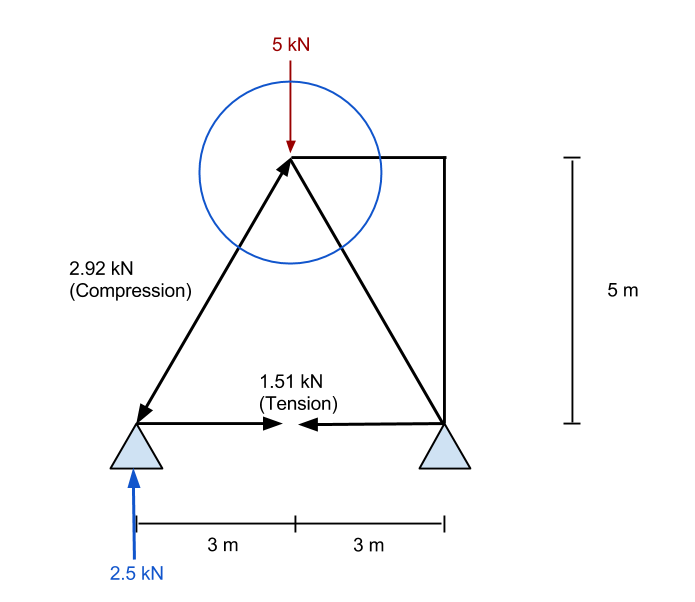
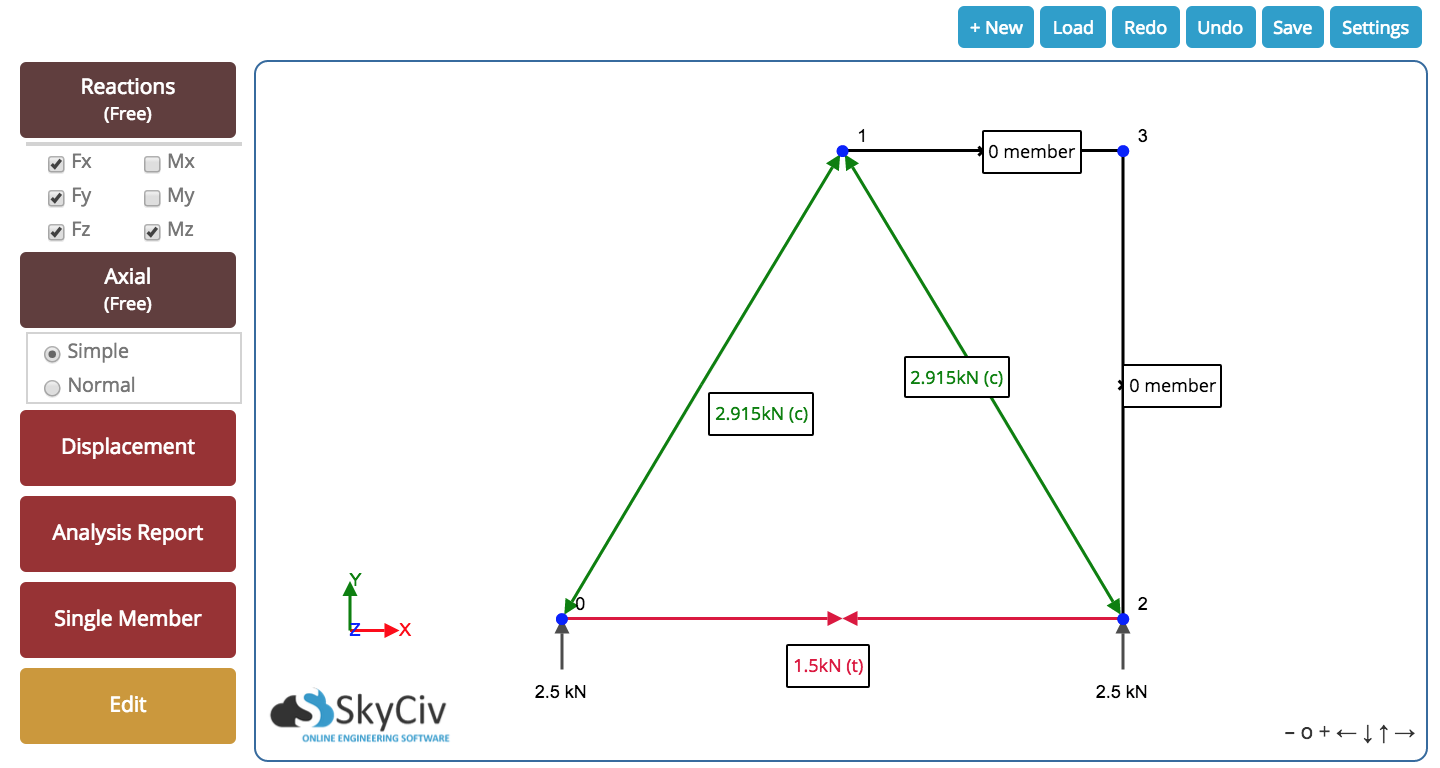
Infine, finiamo con il seguente risultato per il nostro traliccio. Possiamo vedere tutte le forze assiali risultanti all'interno dell'asta e il reazioni agli appoggi. Il seguente risultato è stato preso dal nostro Calcolatore di traliccio gratuito – Provaci, è gratis!
Semplici passaggi
- Inizia sempre calcolando le reazioni ai supporti
- Scegli un punto con una forza nota e guardalo in isolamento
- Usa la geometria vettoriale e la somma delle forze = 0 per risolvere le altre forze membri
- Ripeti il processo finché tutti i membri non sono stati risolti
- Ricordati di fare attenzione a Zero Members
Tutorial pertinente
- Risoluzione del traliccio con il metodo delle sezioni. Include un video e una guida passo passo
Aggiungi Supporti illimitati con il pieno controllo sui loro codici di ritenuta
Aggiungi Supporti illimitati con il pieno controllo sui loro codici di ritenuta può calcolare automaticamente il metodo dei giunti per te. Oppure prova il nostro Calcolatore di traliccio gratuito che ti darà la risposta finale (nessun calcolo manuale).
Per esplorare più funzionalità del software SkyCiv, iscriviti oggi per iniziare!


