Questo articolo discute due esempi di progettazione di solette in cemento armato, compresa la flessione unidirezionale e bidirezionale. L'obiettivo principale è confrontare i risultati ottenuti tra i calcoli manuali e il modulo SkyCiv Plate Design. Useremo l'Eurocodice 2 per strutture in cemento armato.
I codici di costruzione hanno approcci simili quando definiscono i casi tipici per le lastre. Se vuoi saperne di più su questo argomento, vi suggeriamo di leggere i seguenti articoli riguardanti la progettazione dei solai Esempio di progettazione di lastre ACI e confronto con SkyCiv e Standard australiani AS3600 Esempio di progettazione di lastre e confronto con SkyCiv
Esempio di progettazione di lastre unidirezionali
Il primo caso da analizzare è un piccolo edificio ad un piano (figura 1, figura 2) che ha un comportamento a lastre descritto come in una direzione.
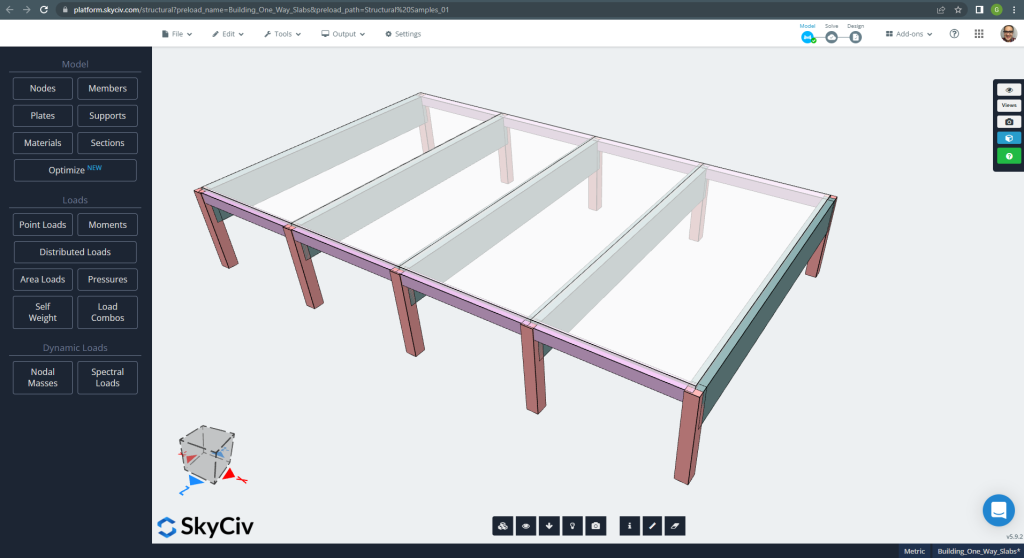
figura 1. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
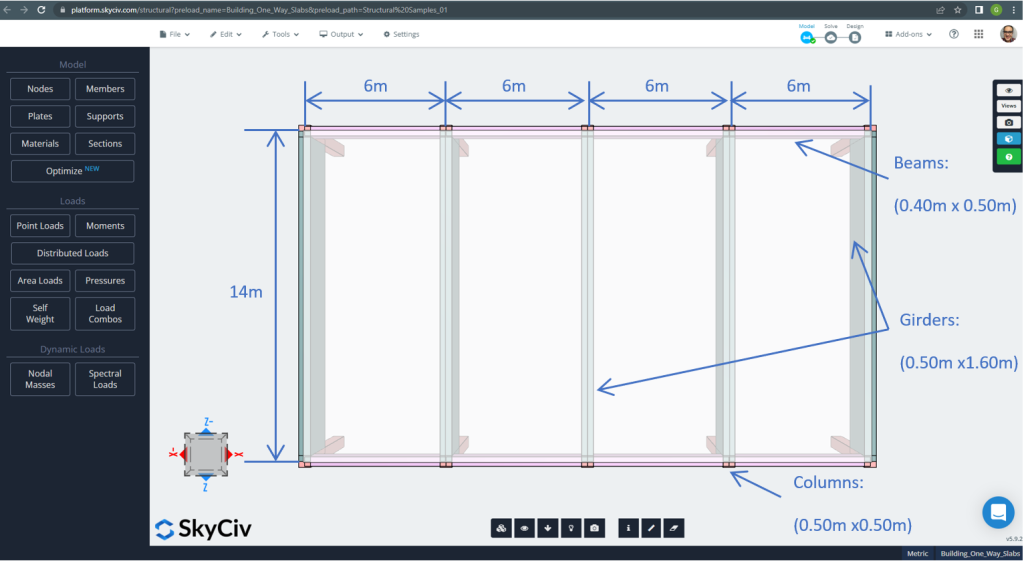
figura 2. Lastre unidirezionali in un piccolo esempio di edificio (dimensioni del piano). (3D strutturale, Ingegneria del cloud SkyCiv).
Per l'esempio della lastra, In sintesi, il materiale, proprietà degli elementi, e carichi da considerare :
- Classificazione del tipo di soletta: Uno – modo di comportamento \(\frac{L_2}{L_1} > 2 ; \frac{14m}{6m}=2.33 > 2.00 \) Ok!
- Occupazione edilizia: Uso residenziale
- Spessore lastra \(t_{lastra}=0,25 m)
- Densità del cemento armato \(\ro_w = 25 \frac{kN}{m^3}\)
- Resistenza a compressione caratteristica del calcestruzzo a 28 giorni (C25\30) \(cazzo = 25 MPa \)
- Peso proprio della lastra \(Dead = \rho_w \times t_{lastra} = 25 \frac{kN}{m^3} \volte 0,25 m = 6.25 \frac {kN}{m^2}\)
- Carico morto sovrapposto \(SD = 3.0 \frac {kN}{m^2}\)
- Carica in tempo reale \(L = 2.0 \frac {kN}{m^2}\)
Calcoli manuali secondo EN-2
In questa sezione, calcoleremo l'armatura in acciaio armato richiesta utilizzando il riferimento dello standard Eurocodice. Per prima cosa otteniamo il momento flettente totale fattorizzato che deve essere svolto dalla striscia di larghezza unitaria della soletta.
- Carico morto, \(g = (3.0 + 6.25) \frac{kN}{m^2} \volte 1 m = 9.25 \frac{kN}{m}\)
- Carica in tempo reale, \(q = (2.0) \frac{kN}{m^2} \volte 1 m = 2.0 \frac{kN}{m}\)
- Carico finale, \(Fd = 1,35volte g + 1.5\volte q = (1.35\volte 9.25 + 1.5\volte 2.0)\frac{kN}{m} =15,5 frac{kN}{m} \)
Prima di ottenere l'area di rinforzo in acciaio, dobbiamo verificare i rapporti di profondità effettivi della campata. Due casi principali:
| Sistema strutturale | Rapporto di profondità effettiva di base | ||
|---|---|---|---|
| Fattore per il sistema strutturale K | Calcestruzzo altamente sollecitato %(\(\ro = 1.5 )\) | Calcestruzzo leggermente sollecitato %(\(\ro = 0.5 )\) | |
| 1. Luce di estremità di trave continua o soletta continua unidirezionale o soletta bidirezionale continua su un lato lungo | 1.3 | 18 | 26 |
| 2. Portata interna di trave continua o soletta portante unidirezionale o bidirezionale | 1.5 | 20 | 30 |
Il caso più critico è per il numero uno, COSÌ, selezioniamo un rapporto di 26.
- \(t_{min}= Frac{L}{LO SO}+copertina+0.5barra dei punti_{diametro}= Frac{6m}{26}+0.025m+0.5volte 12mm=0.26m \) ~ \(0.25M). Lo spessore complessivo è ancora adeguato, Ok!
Adesso, è giunto il momento di utilizzare la tavola per lastre continue unidirezionali:
| Terminare la condizione di supporto | In primo luogo supporto interno | Al centro delle campate interne | A supporti interni | ||||
|---|---|---|---|---|---|---|---|
| Appuntato | Continuo | ||||||
| Supporto esterno | Vicino alla metà della campata finale | Fine del supporto | Portata finale | ||||
| Momento | 0 | 0.086FL | – | 0.075FL | – | 0.063FL | – |
| 0.04FL | 0.086FL | 0.063FL | |||||
| cesoia | 0.4F | – | – | – | |||
| 0.46F | 0.6F | 0.5F | |||||
Dove:
- L è l'intervallo effettivo
- F è il carico ultimo totale nella campata (1.35gr + 1.5Qk; Gk è il carico morto e Qk il carico mobile, rispettivamente)
Sarà spiegato solo un caso (supporto finale continuo) e il resto verrà mostrato nella tabella seguente.
- \(F=Fd\times L = 15.5 \frac{kN}{m} \volte 6m = 93.0 kN \)
- \(M=0.04FL=0.04 \times 93.0 kN \times 6m= -22.32{kN}{m}\)
- \(d = 230 mm \)
- \(K=\frac{M}{{b}{d^2}{f_{Eurocodice di design con piastra di base in acciaio}}}= Frac{22.32\volte 10^6 {N}{mm}}{{1000mm}\volte{(230 mm)^ 2}\volte {25 \frac{N}{mm^2}}}=0.016877\)
- \(l_a = 0.95 \)
- \(z=l_a \times d = 0.95\times 230mm = 218.50 mm\)
- \(A_s = frac{M}{{0.87}{f_{sì}}{z}}= Frac{22.32\volte 10^6 {N}{mm}}{0.87\volte 500 {N}{mm^2} \volte {218.50mm} = 234.83 mm^2 }\)
- \(UN_{S,min}=0.0013{b}{d}=0.0013\times 1000mm \times 230 mm =299 mm^2\)
- \(UN_{sto}= massimo(Come, UN_{S,min}) = massimo(234.83, 299) mm^2 = 299 mm^2 \)
| momenti | Esterno negativo sinistro | Esterno Positivo | Esterno negativo a destra | Interno sinistro negativo | Interno positivo | Interno negativo a destra |
|---|---|---|---|---|---|---|
| Valore M, kN-m | 22.32 | 35.15 | 41.85 | 48.00 | 35.15 | 35.15 |
| K | 0.0168 | 0.0266 | 0.03164 | 0.0362 | 0.0266 | 0.0266 |
| z, mm | 218.50 | 218.50 | 218.50 | 218.50 | 218.50 | 218.50 |
| \(Come, mm^2) | 234.83 | 369.815 | 440.31 | 505.011 | 369.815 | 369.815 |
| \(UN_{S,min},mm^2) | 299.00 | 299.00 | 299.00 | 299.00 | 299.00 | 299.00 |
| \(UN_{sto} {mm^2}\) | 299.00 | 369.815 | 440.31 | 505.011 | 369.815 | 369.815 |
La mossa successiva è calcolare l'acciaio dell'armatura di rinforzo utilizzando il modulo di progettazione della piastra in SkyCiv. per favore, continua a leggere la sezione seguente!.
Se sei nuovo in SkyCiv, Iscriviti e testa tu stesso il software!
Risultati del modulo di progettazione della piastra SkyCiv S3D
Questa sezione si occupa di ottenere l'area dell'armatura in acciaio ma solo utilizzando il software, il Modulo di progettazione della piastra. In modo conciso, mostreremo solo i risultati o le informazioni importanti attraverso le immagini.
Prima di analizzare il modello, dobbiamo definire una dimensione della maglia della piastra. Alcuni riferimenti (2) consiglia una dimensione per l'elemento shell di 1/6 del breve arco o 1/8 del lungo arco, il più corto di loro. A seguito di questo valore, noi abbiamo \(\frac{L2}{6}= Frac{6m}{6} = 1 m \) o \(\frac{L1}{8}= Frac{14m}{8}= 1,75 m \); prendiamo 1 m come dimensione massima consigliata e 0,50 m di dimensione della maglia applicata.
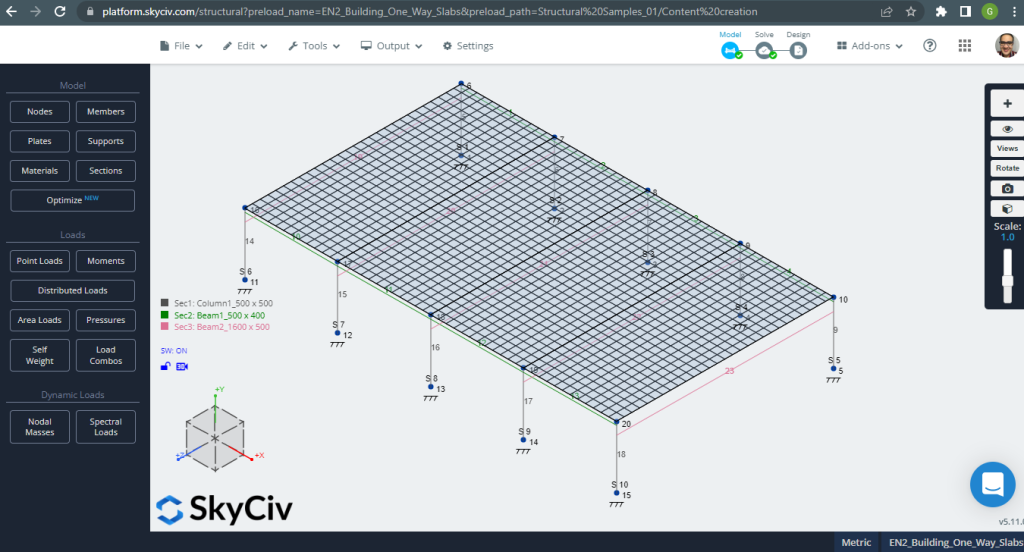
figura 3. Piastra a rete. (3D strutturale, Ingegneria del cloud SkyCiv).
Una volta migliorato il nostro modello strutturale analitico, eseguiamo un'analisi elastica lineare. Quando si progettano lastre, dobbiamo verificare se gli spostamenti verticali sono inferiori al massimo consentito dal codice. Eurocodice 2 ha stabilito uno spostamento verticale di massima manutenibilità di \(\frac{L}{250}= Frac{6000mm}{250}=24,0mm).
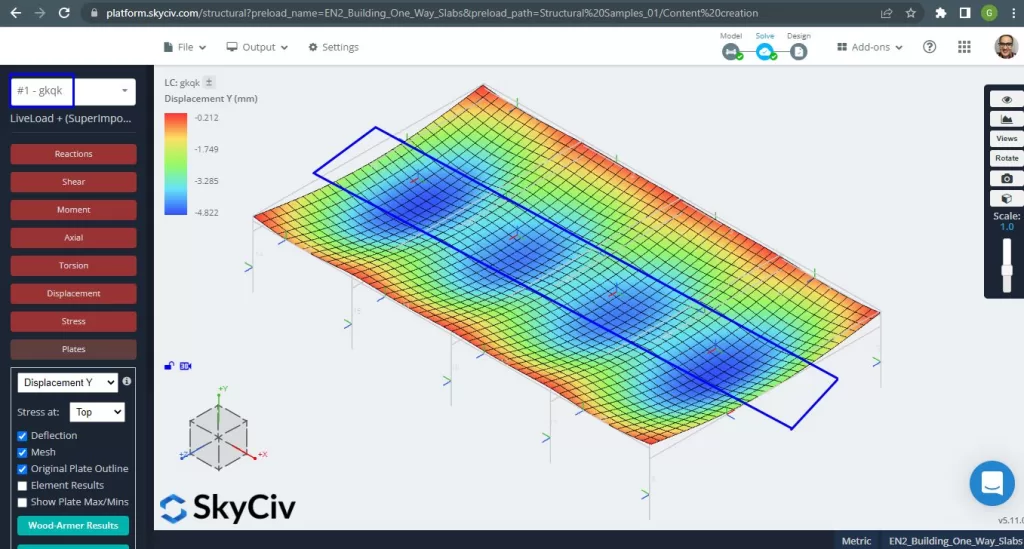
figura 4. Spostamento verticale, valori massimi al centro delle campate. (3D strutturale, Ingegneria del cloud SkyCiv).
Confronto tra lo spostamento verticale massimo e il valore di riferimento del codice, la rigidezza della soletta è adeguata. \(4.822 mm < 24.00mm\).
I momenti massimi nelle luci della soletta si trovano per positivo al centro e per negativo agli appoggi esterni ed interni. Vediamo i valori di questi momenti nelle seguenti immagini.
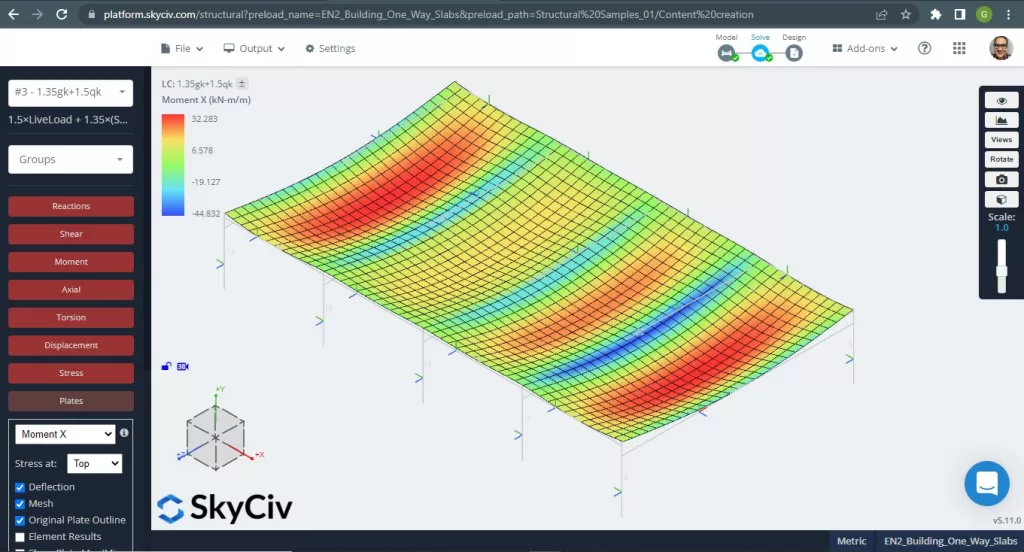
figura 5. Momenti flettenti in direzione X. (3D strutturale, Ingegneria del cloud SkyCiv).
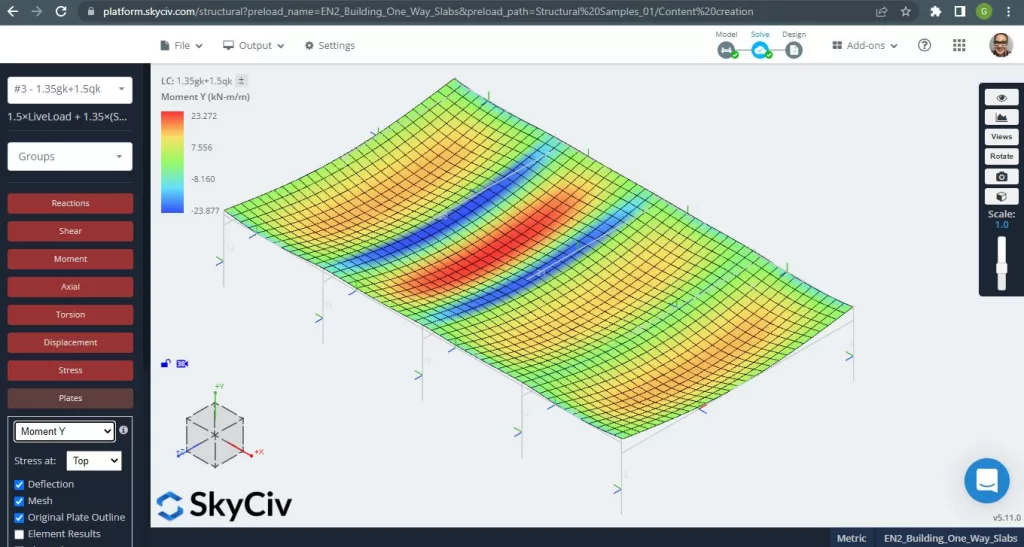
figura 6. Momenti flettenti in direzione Y. (3D strutturale, Ingegneria del cloud SkyCiv).
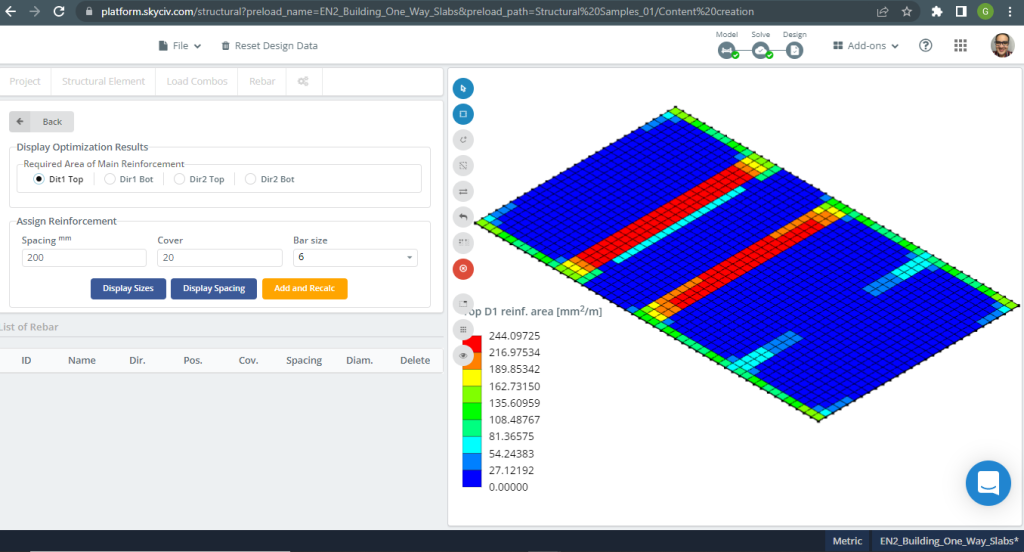
figura 7. Rinforzo in acciaio per la direzione X in alto. (3D strutturale, Ingegneria del cloud SkyCiv).
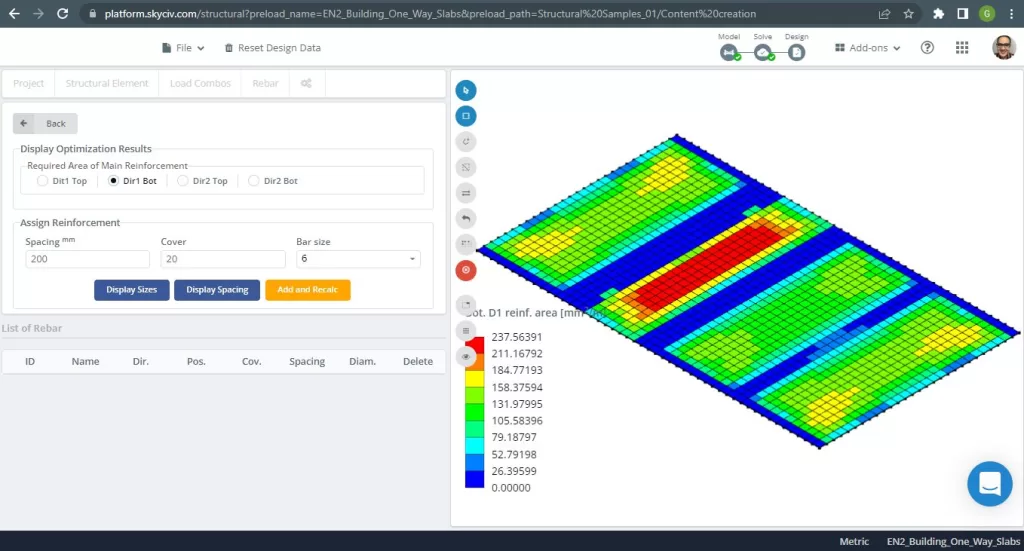
figura 8. Rinforzo in acciaio per la direzione X in basso. (3D strutturale, Ingegneria del cloud SkyCiv).
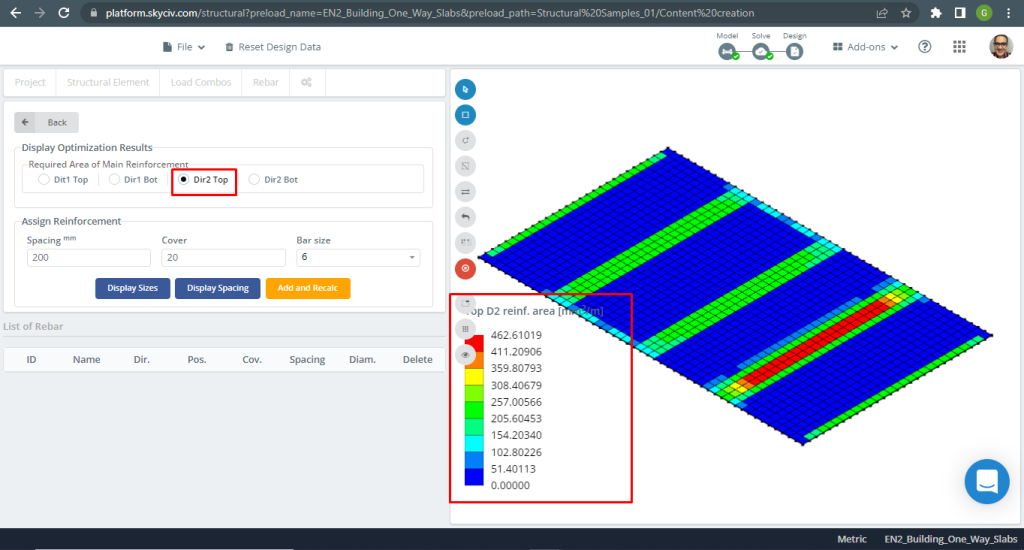
figura 9. Rinforzo in acciaio per la direzione Y in alto. (3D strutturale, Ingegneria del cloud SkyCiv).
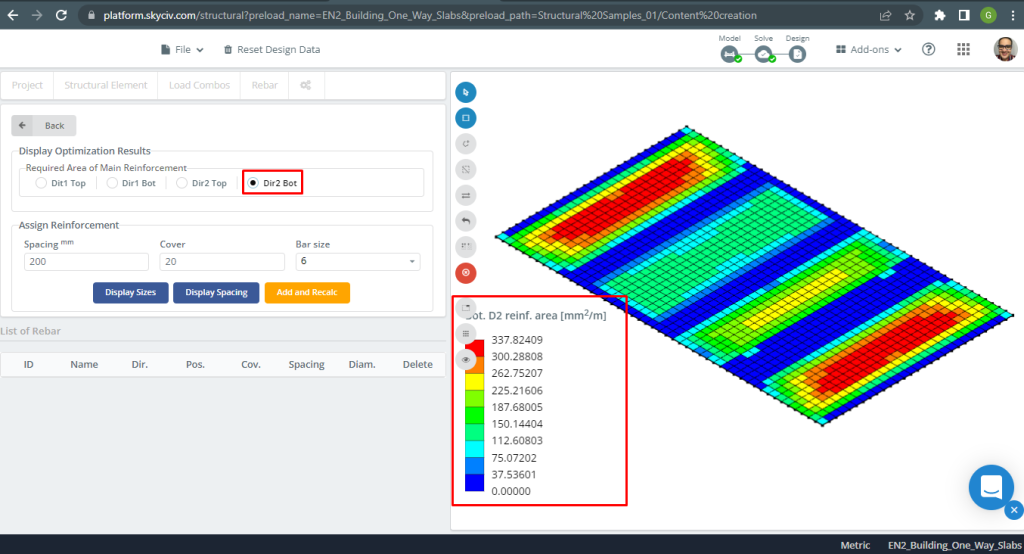
figura 10. Rinforzo in acciaio per la direzione Y in basso. (3D strutturale, Ingegneria del cloud SkyCiv).
Confronto dei risultati
L'ultimo passaggio in questo esempio di progettazione di solaio unidirezionale è confrontare l'area dell'armatura in acciaio ottenuta dall'analisi S3D (assi locali “2”) e calcoli manuali.
| Momenti e area d'acciaio | Esterno negativo sinistro | Esterno Positivo | Esterno negativo a destra | Interno sinistro negativo | Interno positivo | Interno negativo a destra |
|---|---|---|---|---|---|---|
| \(UN_{sto, HandCalc} {mm^2}\) | 299.00 | 369.82 | 440.31 | 505.011 | 369.82 | 369.82 |
| \(UN_{sto, S3D} {mm^2}\) | 308.41 | 337.82 | 462.61 | 462.61 | 262.75 | 308.41 |
| \(\Delta_{dif}\) (%) | 3.051 | 8.653 | 4.820 | 8.400 | 28.95 | 16.610 |
Possiamo vedere che i risultati dei valori sono molto vicini tra loro. Questo significa che i calcoli sono corretti!
Se sei nuovo in SkyCiv, Iscriviti e testa tu stesso il software!
Esempio di progettazione di solette a due vie
SkyCiv 3D Plate Design Module è un potente software in grado di analizzare e progettare qualsiasi tipo di edificio che puoi immaginare. Per il secondo esempio di lastra di progettazione, abbiamo deciso di eseguire un sistema a soletta piana (figura 11).
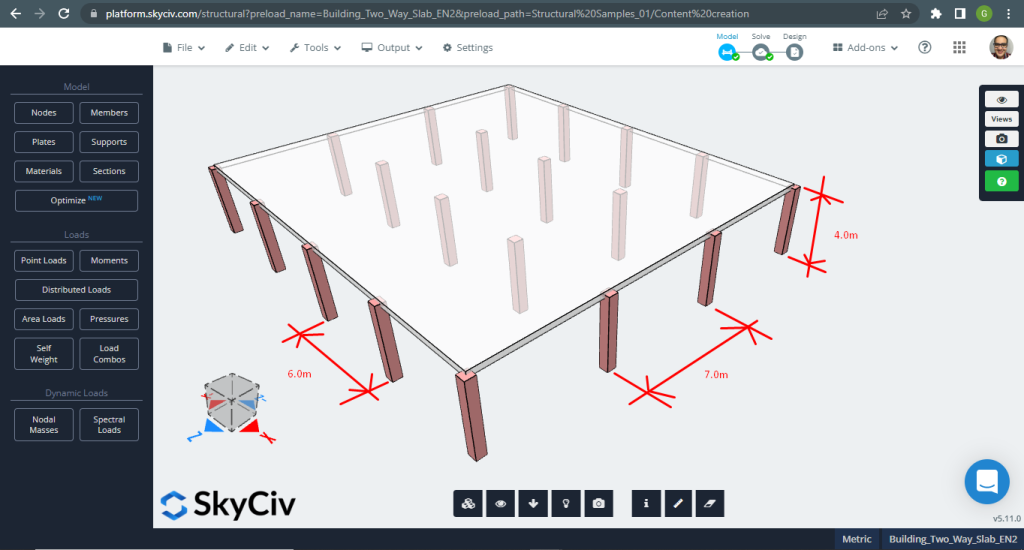
figura 11. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
Per l'esempio della lastra, In sintesi, il materiale, proprietà degli elementi, e carichi da considerare :
- Classificazione del tipo di soletta: Due – modo di comportamento \(\frac{L_2}{L_1} \il 2 ; \frac{7m}{6m}=1.17 le 2.00 \) Ok!
- Occupazione edilizia: Uso residenziale
- Spessore lastra \(t_{lastra}=0,30 m)
- Densità del cemento armato \(\ro_w = 25 \frac{kN}{m^3}\)
- Resistenza a compressione caratteristica del calcestruzzo a 28 giorni (C25\30) \(cazzo = 25 MPa \)
- Peso proprio della lastra \(Dead = \rho_w \times t_{lastra} = 25 \frac{kN}{m^3} \volte 0,30 m = 7.5 \frac {kN}{m^2}\)
- Carico morto sovrapposto \(SD = 3.0 \frac {kN}{m^2}\)
- Carica in tempo reale \(L = 2.0 \frac {kN}{m^2}\)
Calcoli manuali secondo EN-2
Il primo passo è definire il carico massimo totale:
- Carico morto, \(g = (3.0 + 7.5) \frac{kN}{m^2} \volte 7 m = 73.50 \frac{kN}{m}\)
- Carica in tempo reale, \(q = (2.0) \frac{kN}{m^2} \volte 7 m = 14.00 \frac{kN}{m}\)
- Carico finale, \(Fd = 1,35volte g + 1.5\volte q = (1.35\volte 73.50 + 1.5\volte 14.00)\frac{kN}{m} =120.225 \frac{kN}{m} \)
Per il calcolo manuale, la struttura deve essere suddivisa in una serie di telai equivalenti. Possiamo utilizzare i seguenti metodi per raggiungere questo obiettivo:
- Distribuzione dei momenti (Metodo Hardy Cross) per l'analisi del telaio.
- Metodo di rigidità per l'analisi del telaio al computer. Prova il nostro Calcolatore della matrice di rigidità.
- Un metodo semplificato che utilizza i coefficienti dei momenti per la direzione unidirezionale adattato ai seguenti requisiti (Abbiamo scelto questo metodo per la semplicità del modello analizzato):
- La stabilità laterale non dipende dai collegamenti soletta-colonna (Non analizziamo l'edificio per i carichi laterali);
- Sono presenti almeno tre file di pannelli di campata approssimativamente uguale nella direzione considerata (Abbiamo quattro e tre file di pannelli in entrambe le direzioni principali);
- La dimensione della baia supera \(30m^2) (La nostra area modello è \(42m^2)
Lo spessore selezionato per l'esempio di solaio è maggiore del valore minimo massimo per la resistenza al fuoco indicato nella tabella sottostante.
| Resistenza al fuoco standard | Dimensioni minime (mm) | |
|---|---|---|
| Spessore lastra, hs | Distanza dell'asse, un carico | |
| REI 60 | 180 | 15 |
| REI 90 | 200 | 25 |
| REI 120 | 200 | 35 |
| REI 240 | 200 | 50 |
In questa sezione, svilupperemo solo i calcoli per la direzione longitudinale e la striscia di colonne (sentiti libero di calcolare per un'altra direzione, il trasversale, e per le strisce centrali). Prima di approfondire i numeri, per prima cosa dobbiamo dividere in strisce: centrale e colonna. (Per maggiori dettagli sulle strisce di design, controlla questo articolo di SkyCiv: Progettare lastre con ACI-318).
- Larghezza della striscia della colonna: \(6m/4 = 1,50 m)
- Larghezza striscia centrale: \(7m – 2\times 1.50m = 4.0m\)
EC2 consente di assegnare i momenti in ogni striscia di progettazione secondo la seguente tabella
| Striscia di colonne | Striscia di mezzo | |
|---|---|---|
| Momento negativo al bordo colonna | 100% ma non più di \(0.17{Essere}{d^2}{f_{Eurocodice di design con piastra di base in acciaio}}\) | 0 |
| Momento negativo alla colonna interna | 60-80% | 40-20% |
| Momento positivo in span | 50-70% | 50-30% |
Abbiamo selezionato le percentuali di momenti per la striscia di colonne in analisi:
- Momento negativo al bordo colonna: 100%.
- Momento negativo alla colonna interna: 80%
- Momento positivo in span: 70%
Calcolo dei momenti totali delle strisce di progetto:
| Terminare la condizione di supporto | In primo luogo supporto interno | Al centro delle campate interne | A supporti interni | ||||
|---|---|---|---|---|---|---|---|
| Appuntato | Continuo | ||||||
| Supporto esterno | Vicino alla metà della campata finale | Fine del supporto | Portata finale | ||||
| Momento | 0 | 0.086FL | – | 0.075FL | – | 0.063FL | – |
| 0.04FL | 0.086FL | 0.063FL | |||||
| cesoia | 0.4F | – | – | – | |||
| 0.46F | 0.6F | 0.5F | |||||
Dove:
- L è l'intervallo effettivo
- F è il carico ultimo totale nella campata (1.35gr + 1.5Qk; Gk è il carico morto e Qk il carico mobile, rispettivamente)
Sarà spiegato solo un caso (supporto finale continuo) e il resto verrà mostrato nella tabella seguente.
- \(F=Fd\times L = 120.225 \frac{kN}{m} \volte 6m = 721.35 kN \)
- \(M=0.04FL=0.04 \times 721.35 kN \times 6m= -173.124 {kN}{m}\)
- \(d = 280 mm \)
- \(K=\frac{M}{{b}{d^2}{f_{Eurocodice di design con piastra di base in acciaio}}}= Frac{173.124\volte 10^6 {N}{mm}}{{1500mm}\volte{(280 mm)^ 2}\volte {25 \frac{N}{mm^2}}}=0,012637)
- \(l_a = 0.95 \)
- \(z=l_a \times d = 0.95\times 280mm = 266.0 mm\)
- \(A_s = frac{M}{{0.87}{f_{sì}}{z}}= Frac{173.124\volte 10^6 {N}{mm}}{0.87\volte 500 {N}{mm^2} \volte {266.0mm} = 214.0523 mm^2 }\)
- \(UN_{S,min}=0.0013{b}{d}=0.0013\times 1500mm \times 280 mm =546 mm^2\)
- \(UN_{sto}= massimo(Come, UN_{S,min}) = massimo(234.83, 546) mm^2 = 299 mm^2 \)
| momenti | Esterno negativo sinistro | Esterno Positivo | Esterno negativo a destra | Interno sinistro negativo | Interno positivo | Interno negativo a destra |
|---|---|---|---|---|---|---|
| Valore M, kN-m | 173.124 | 191.125 | 260.064 | 298.281 | 191.125 | 218.429 |
| K | 0.05897 | 0.06500 | 0.0884 | 0.101 | 0.06500 | 0.0743 |
| z, mm | 266.00 | 266.00 | 266.00 | 266.00 | 266.00 | 266.00 |
| \(Come, mm^2) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
| \(UN_{S,min},mm^2) | 546.00 | 546.00 | 546.00 | 546.00 | 546.00 | 546.00 |
| \(UN_{sto} {mm^2}\) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
La mossa successiva è calcolare l'acciaio dell'armatura di rinforzo utilizzando il modulo di progettazione della piastra in SkyCiv. per favore, continua a leggere la sezione seguente!
Risultati del modulo di progettazione della piastra SkyCiv S3D
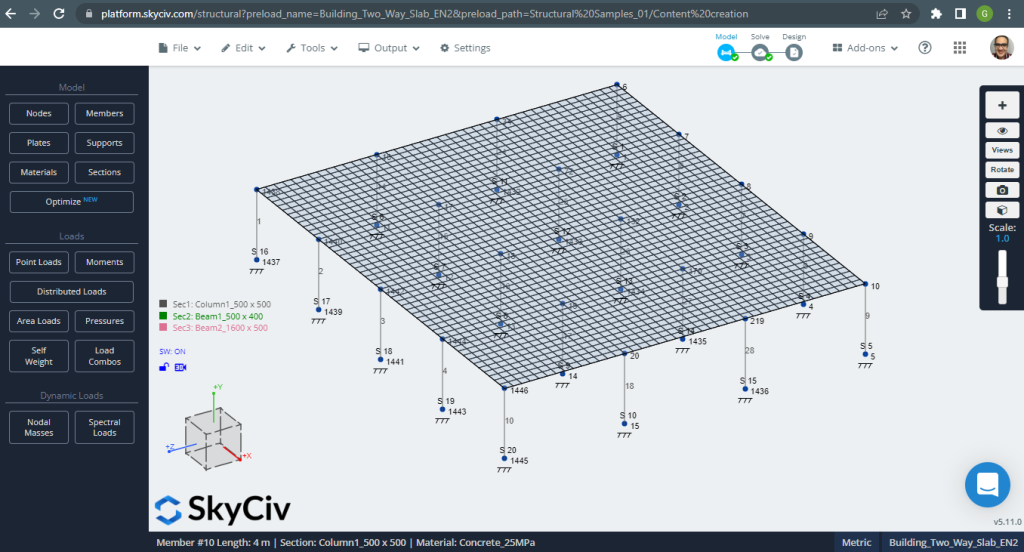
figura 12. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
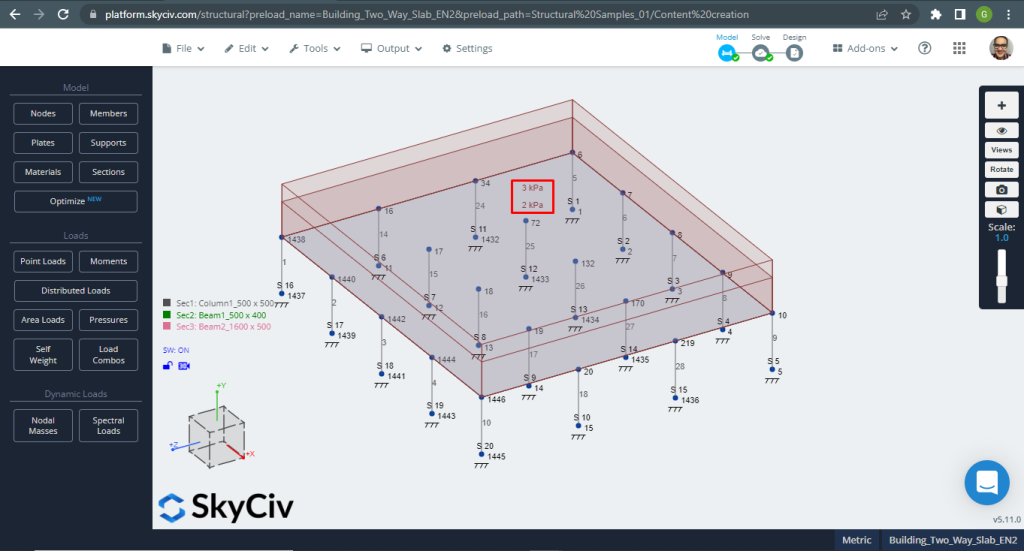
figura 13. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
Quando si progettano lastre, dobbiamo verificare se gli spostamenti verticali sono inferiori al massimo consentito dal codice. L'Eurocodice ha stabilito uno spostamento verticale massimo di manutenibilità di \(\frac{L}{250}= Frac{6000mm}{250}=24,0mm).
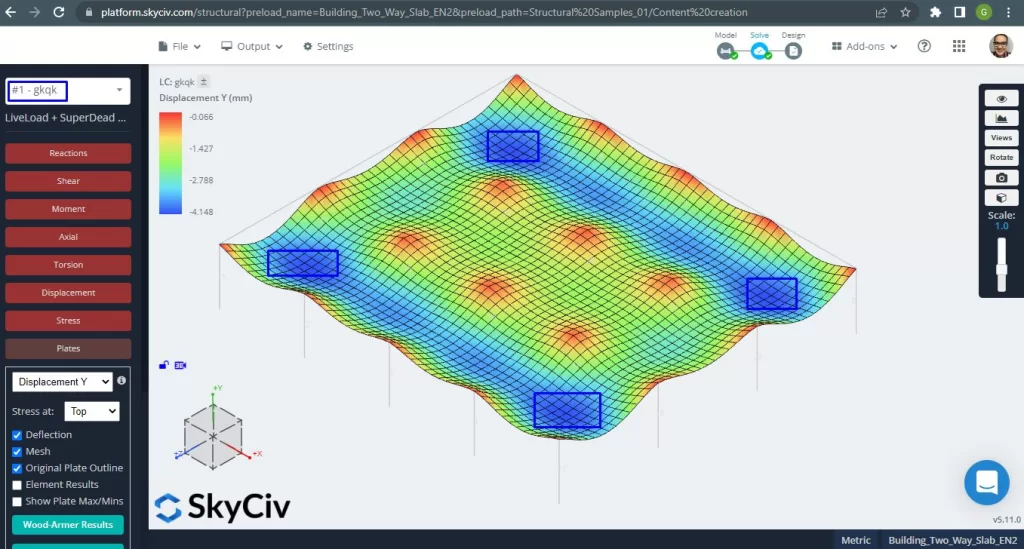
figura 14. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
L'immagine sopra ci dà lo spostamento verticale. Il valore massimo è -4,148 mm, inferiore al massimo consentito di -24 mm. Pertanto, la rigidezza della soletta è adeguata.
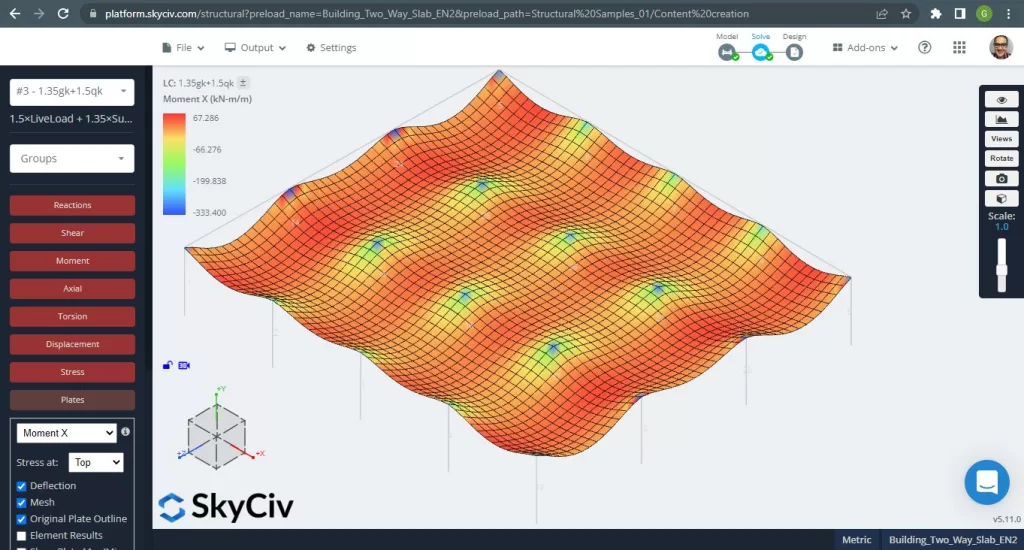
figura 15. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
immagini 15 e 16 sono costituiti dal momento flettente in ciascuna direzione principale. Prendendo la distribuzione del momento ei valori, il software, SkyCiv, può quindi ottenere l'area totale dell'armatura in acciaio.

figura 16. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
Aree di rinforzo in acciaio:
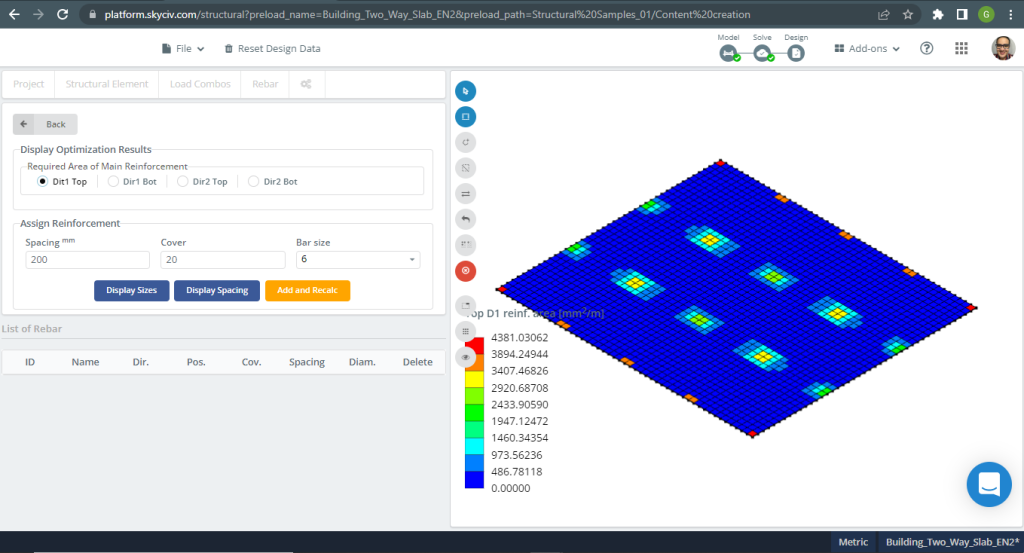
figura 17. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
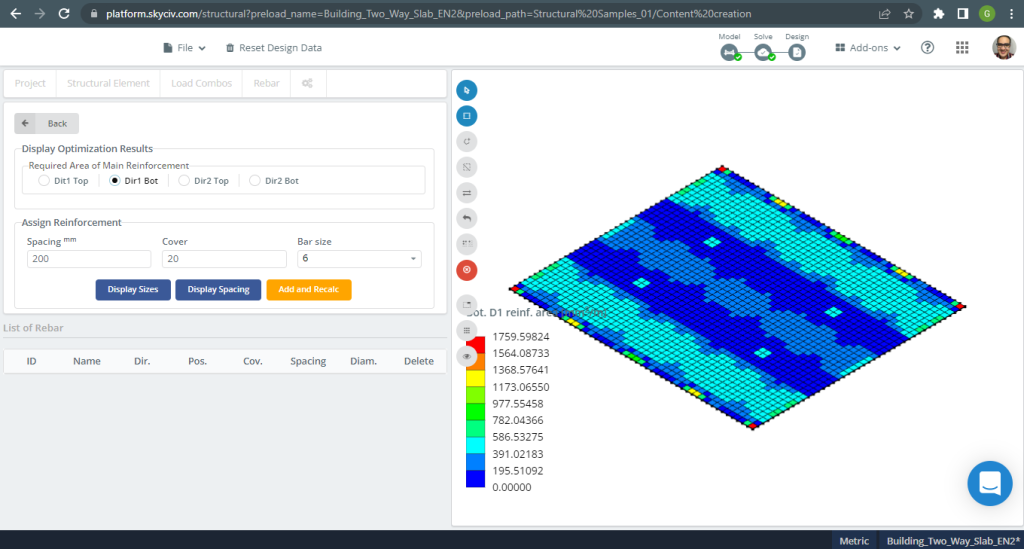
figura 18. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
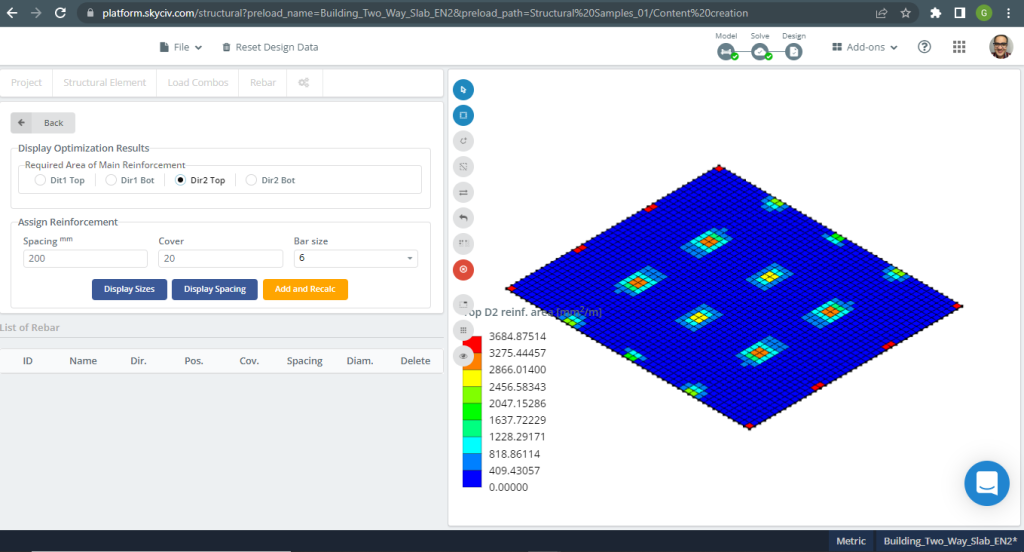
figura 19. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
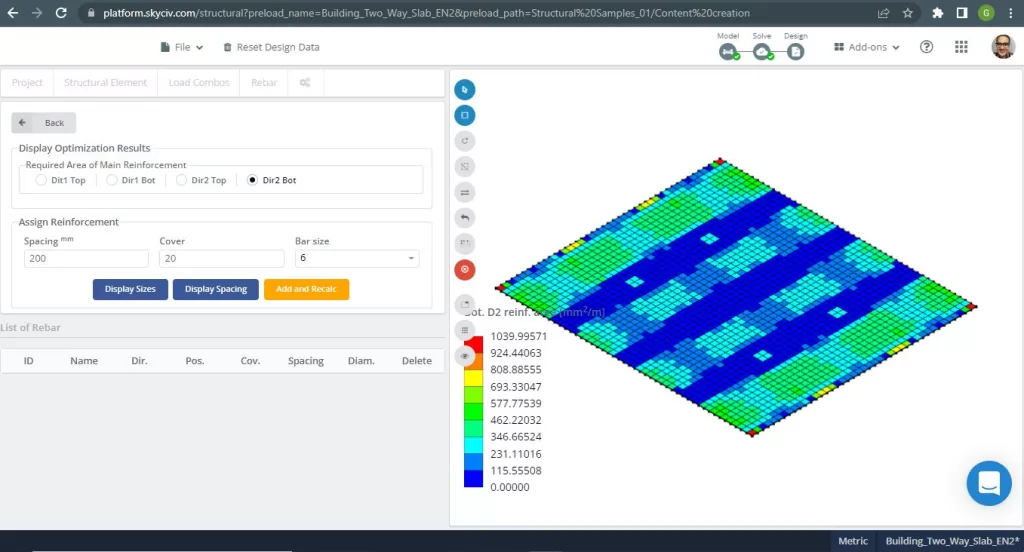
figura 20. Lastre unidirezionali in un piccolo esempio di edificio. (3D strutturale, Ingegneria del cloud SkyCiv).
Confronto dei risultati
L'ultimo passaggio in questo esempio di progettazione di solette a due vie consiste nel confrontare l'area dell'armatura in acciaio ottenuta dall'analisi S3D e dai calcoli manuali.
Acciaio per armature per la direzione X e la striscia della colonna
| Momenti e area d'acciaio | Esterno negativo sinistro | Esterno Positivo | Esterno negativo a destra | Interno sinistro negativo | Interno positivo | Interno negativo a destra |
|---|---|---|---|---|---|---|
| \(UN_{sto, HandCalc} {mm^2}\) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
| \(UN_{sto, S3D} {mm^2}\) | 3889.375 | 1040.00 | 4196.145 | 4196.145 | 520.00 | 3175.00 |
| \(\Delta_{dif}\) (%) | 61.475 | 37.04 | 46.44 | 38.566 | 68.52 | 40.544 |
Se sei nuovo in SkyCiv, Iscriviti e testa tu stesso il software!
Riferimenti
- B. Mosley, R. Ulse, JH. Bungey , “Progettazione in cemento armato secondo l'Eurocodice 2”, Settima edizione, Palgrave MacMillan.
- Bazan Enrico & Melì Piralla, “Progettazione Sismica delle Strutture”, 1ed, CHIARO.
- Eurocodice 2: Progettazione di strutture in calcestruzzo.


