Un esempio completamente funzionante di NBCC 2015 calcoli del carico di neve
L'accumulo di neve sulle strutture può essere molto pericoloso per i membri del tetto o altri elementi strutturali esposti. La National Building Code of Canada (2015) Divisione B – Sezione 4.1.6 fornisce un calcolo dettagliato dei carichi di neve e dei carichi di pioggia associati. Utilizzando questa linea guida, dimostreremo come calcolare i carichi di neve utilizzando un esempio 3D strutturale (S3D) modello di magazzino, come mostrato di seguito:
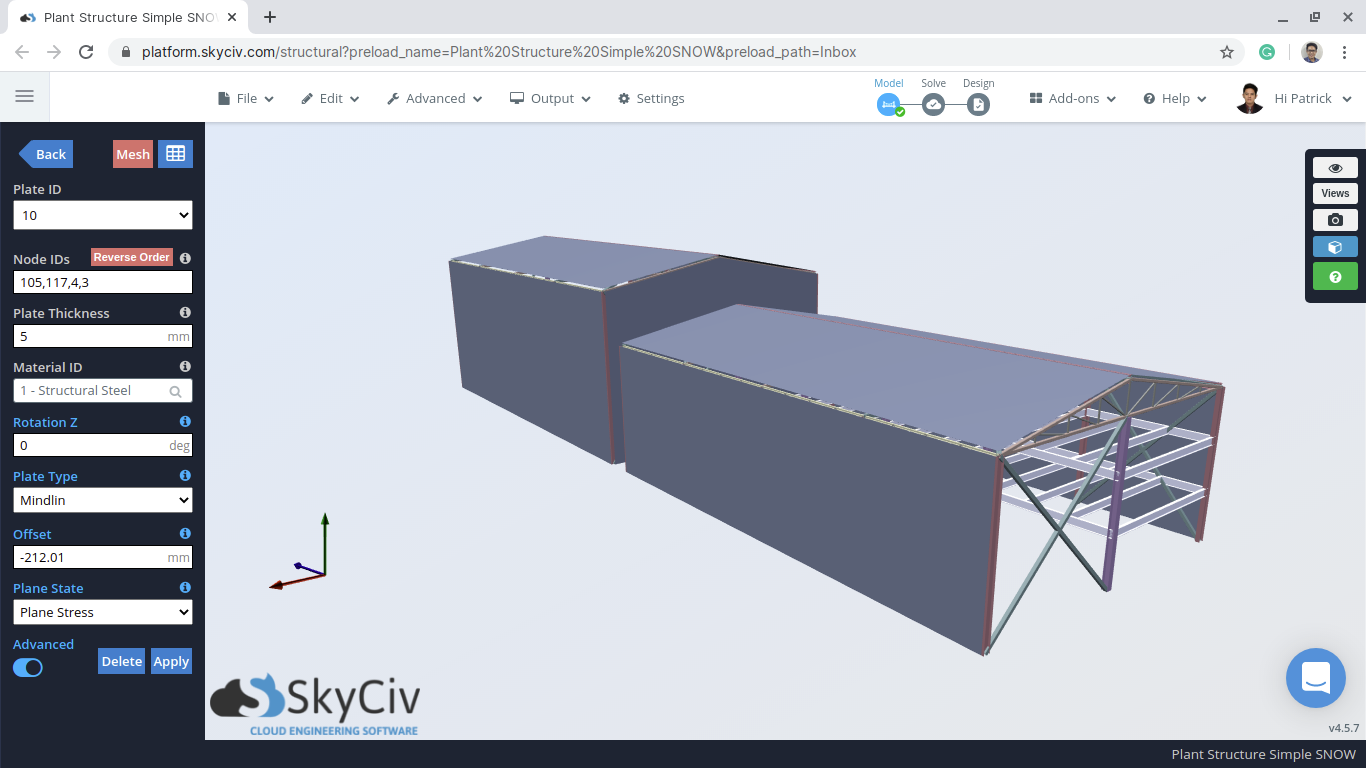
figura 1: Esempio di modello di magazzino S3D
figura 2: Esempio di posizione del sito utilizzando Google Maps (solo a scopo illustrativo).
tavolo 1: Dati di costruzione necessari per il nostro calcolo del carico di neve.
| Posizione | Ogden, Calgary, Alberta (solo a scopo illustrativo) |
| occupazione | Magazzino o stoccaggio di materiali |
| Dimensioni | 19.508 m x 31.70 m per ogni struttura Altezza gronda di un edificio più piccolo 9.144 m Altezza dell'apice di un edificio più piccolo 11.941 m La differenza del tetto superiore e inferiore è 3.50 m Angolo di inclinazione del tetto 16° |
| dettagli aggiuntivi | Il tetto ha una superficie scivolosa Il divario tra le strutture è 2.30 m |
Dalla tabella 1, il carico di neve specificato, \(S), può essere calcolato utilizzando la formula:
\(S = {I}_{S}[{S}_{S}{C}_{b}{C}_{w}{C}_{S}{C}_{un carico} +{S}_{r}]\) (1)
Dove:
\({I}_{S}\) = fattore di importanza per il carico di neve, Tabella 4.1.6.2-A
\({S}_{S}\) = 1-carico di neve al suolo in 50 anni, kPa, Sottosezione 1.1.3
\({C}_{b}\) = fattore di carico di base della neve sul tetto, 4.1.6.2 (2)
\({C}_{w}\) = in base al fattore di esposizione al vento, 4.1.6.2 (3) e (4)
\({C}_{S}\) = fattore di pendenza, 4.1.6.2 (5), (6), e (7)
\({C}_{un carico}\) = fattore di accumulo, 4.1.6.2 (8)
\({S}_{r}\) = Carico di pioggia associato da 1 su 50 anni, kPa, Sottosezione 1.1.3, ma non maggiore di \({S}_{S}{C}_{b}{C}_{w}{C}_{S}{C}_{un carico}\)
Ogni parametro verrà esaminato singolarmente nelle sezioni seguenti. Verranno calcolati i seguenti casi di carico neve: carico di neve equilibrato e sbilanciato su ogni tetto (vento normale al crinale), così come la deriva generata sul tetto inferiore considerando l'accumulo da scorrimento.
Fattore di importanza, \({I}_{S}\)
La prima cosa che viene determinata è il fattore di importanza, \({I}_{S}\), che si trova utilizzando Tabella 4.1.6.2-A come referenziato. Poiché la struttura è un edificio di stoccaggio che ha un basso impatto diretto sulla vita umana in caso di guasto, la categoria di importanza è Basso. Inoltre, il calcolo avverrà nello Stato limite ultimo (ULS). Quindi da Tabella 4.1.6.2-A, \({I}_{S}\) è uguale a 0.80.
| Categoria di importanza | Fattore di importanza, \({I}_{S}\) | |
|---|---|---|
| ULS | SLS | |
| Basso | 0.8 | 0.9 |
| Normale | 1.0 | 0.9 |
| Alto | 1.15 | 0.9 |
| Post-disastro | 1.25 | 0.9 |
Carico di neve al suolo, \({S}_{S}\), e carico di pioggia associato, \(({S}_{r})\)
Il carico di neve al suolo, \({S}_{S}\), e il carico di pioggia associato, \(({S}_{r})\), i valori sono tabulati in Appendice C., Divisione B di NBCC 2015 a seconda della località e della provincia. Per questo esempio, il corrispondente \({S}_{S}\) e \(({S}_{r})\) pollici Calgary Alberta è uguale a 1.10 kPa e 0.1 kPa, rispettivamente.
Avendo difficoltà a cercare la neve al suolo e il carico di pioggia associato per NBCC 2015? Provare il SkyCiv Free Load Generator Tool per velocizzare la ricerca e ottenere il corrispondente \({S}_{S}\) e \({S}_{r}\) in base alla posizione della tua struttura.
Fattore di esposizione al vento, \({C}_{w}\)
Per il fattore di esposizione al vento, \({C}_{w}\), è ammesso che sia uguale a 1.0 in base a 4.1.6.2 (3). Questo fattore può ancora essere ridotto fintanto che le condizioni in 4.1.6.2 (4) è soddisfatto. Per questo esempio, \({C}_{w}\) deve essere uguale a 1.0 poiché la posizione non è un terreno aperto che espone completamente la struttura al vento.
Fattore di carico di base della neve sul tetto, \({C}_{b}\)
Il fattore di carico di base della neve sul tetto, \({C}_{b}\), può essere calcolato utilizzando le seguenti formule, come indicato in 4.1.6.2 (2):
\({C}_{b} = 0.8\) (2) per \({l}_{c} ≤ (70/{{C}_{w}}^{2})\) e
\({C}_{b} = (1/{C}_{w}) [1 – (1 – 0.8{C}_{w})exp(-0.01({l}_{c}{{C}_{w}}^{2} – 70))] \) (3) per \({l}_{c} > (70/{{C}_{w}}^{2})\)
Dove:
\({l}_{c}\) = lunghezza caratteristica del tetto superiore o inferiore definita come: \(2w -{w}^{2}/l\)
\(l\) = maggiore dimensione in pianta del tetto
\(w\) = minore dimensione in pianta del tetto
Per questo esempio,\(l\) e \(w\) è uguale a 31.7 me 19.51 m, rispettivamente, quindi, \({l}_{c}\) è uguale a 27.01. Da \({l}_{c}\) è meno di \((70/{1.0}^{2})\), il fattore di carico di base della neve sul tetto, \({C}_{b}\), è uguale a 0.8.
Fattore di pendenza, \({C}_{S}\)
Il calcolo del fattore di pendenza è \({C}_{S}\) dettagliato in 4.1.6.2 (5), (6), e (7) è mostrato di seguito.
Per tetto scivoloso senza ostacoli:
\({C}_{S} = 1.0\) per \(α ≤ 15°\)
\({C}_{S} = 0\) per \(un' > 60°\)
\({C}_{S} = (60° – un')/45°\) per \(15° < α ≤ 60°\)
Per altri casi:
\({C}_{S} = 1.0\) per \(α ≤ 30°\)
\({C}_{S} = 0\) per \(un' > 70°\)
\({C}_{S} = (70° – un')/40°\) per \(30° < α ≤ 70°\)
Peso specifico della neve, \(γ\)
Il peso specifico della neve è specificato in 4.1.6.13 e deve essere considerato come:
\(γ = 0.43{S}_{S} + 2.2 kN /{m}^{3} ≤ 4,0 kN /{m}^{3}\) (4)
Per questo esempio, \(γ\) è uguale a \(2.673 kN /{m}^{3}\).
Fattore di accumulo, \({C}_{un carico}\)
Fattore di accumulo, \({C}_{un carico}\), l l 4.1.6.2 (8). l.
Carico di neve specificato, \(S)
In questa sezione, il carico di neve specificato, \(S), sarà calcolato per i casi bilanciati e derapati.
Case bilanciato / non alla deriva
Per il caso bilanciato / non deviato, il fattore di accumulo \({C}_{un carico}\) è uguale a 1.0. Inoltre, l \(α\) è \(16°\) e si presume che la superficie del tetto sia scivolosa senza ostacoli, il fattore di pendenza, \({C}_{S}\), per il nostro esempio è uguale a 0.978. Usando l'equazione (1), il carico di neve specificato, \(S), per il caso bilanciato / non deviato è:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa
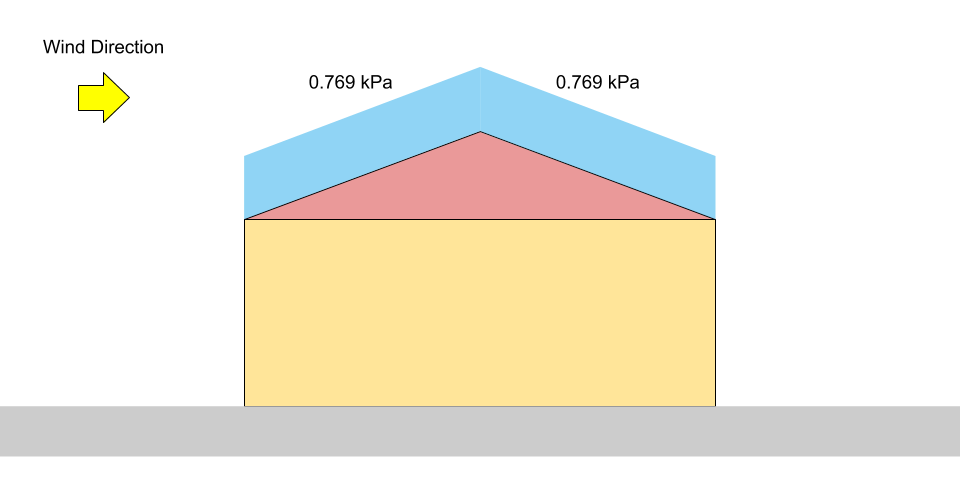
figura 3: Diagramma di carico per carico neve equilibrato su un tetto a due falde.
Case sbilanciato / alla deriva
Vento normale alla cresta
Poiché le strutture hanno tetti a due falde, il carico di neve sbilanciato (vento che agisce normalmente sulla cresta) fattore di accumulo \({C}_{un carico}\) si trova utilizzando 4.1.6.9:
\({C}_{un carico, bolina} = 0\)
\({C}_{un carico, sottovento} = 0.25 +α/20\) per \(15° ≤ α ≤ 20°\)
\({C}_{un carico, sottovento} = 1.25\) per \(20° < α ≤ 90°\)
Perché entrambe le strutture hanno un angolo di inclinazione del tetto pari a 16 °, i fattori di accumulo \({C}_{un carico, bolina}\) e \({C}_{un carico, sottovento}\) sono uguali a 0 e 1.05, rispettivamente. Inoltre, l \(α\) è \(16°\) e si presume che la superficie del tetto sia scivolosa senza ostacoli, il fattore di pendenza, \({C}_{S}\), per il nostro esempio è uguale a 0.978.
In caso di sbilanciamento / deriva normale alla cresta, \({C}_{un carico}\) deve essere calcolato in base a 4.1.6.9 per un caso del tetto a due falde. Dal calcolo sopra, \({C}_{un carico, bolina} = 0\) e \({C}_{un carico, sottovento} = 1.05\). Quindi, i carichi di neve specificati per ogni lato sono:
\({S}_{bolina} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({p}_{1}\)
\({S}_{sottovento} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({p}_{2}\)
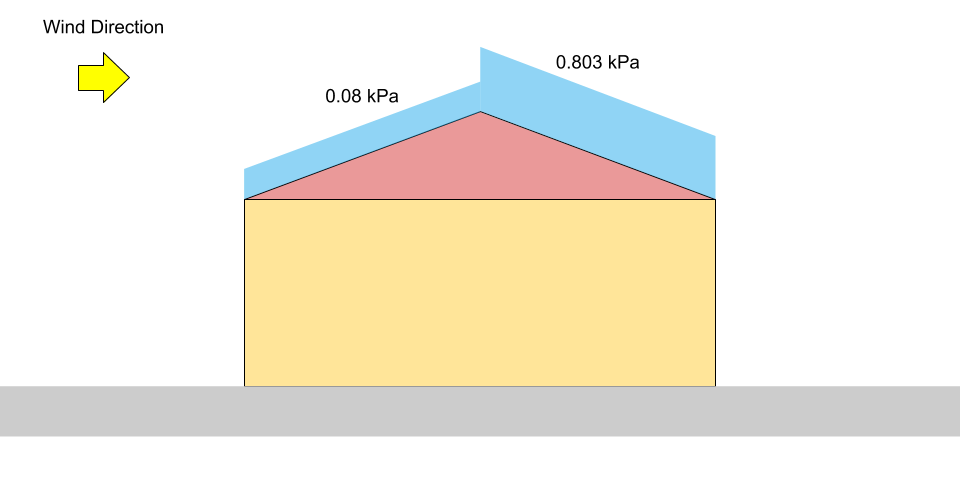
figura 4: Diagramma di carico per carico neve sbilanciato su un tetto a due falde (non in scala).
Vento che agisce parallelamente alla cresta – Caso I. – Vento dal tetto superiore a quello inferiore
Quando il vento agisce parallelamente alla cresta, molto probabilmente si svilupperà un cumulo di neve sul tetto inferiore. l fattore di accumulo \({C}_{un carico}\), le seguenti formule da 4.1.6.2 (8) sono usati:
\({C}_{un carico} ={C}_{a0} – ({C}_{a0} – 1)(X/{x}_{d})\) per \(0 ≤ x ≤ {x}_{d}\)
\({C}_{un carico} = 1.0\) per \(x > {x}_{d}\)
Dove:
\({C}_{a0}\) = valore di picco di \({C}_{a0}\) in x = 0
\(X) = distanza dal gradino del tetto
\({x}_{d}\) = lunghezza della deriva come mostrato in figura 3 sotto
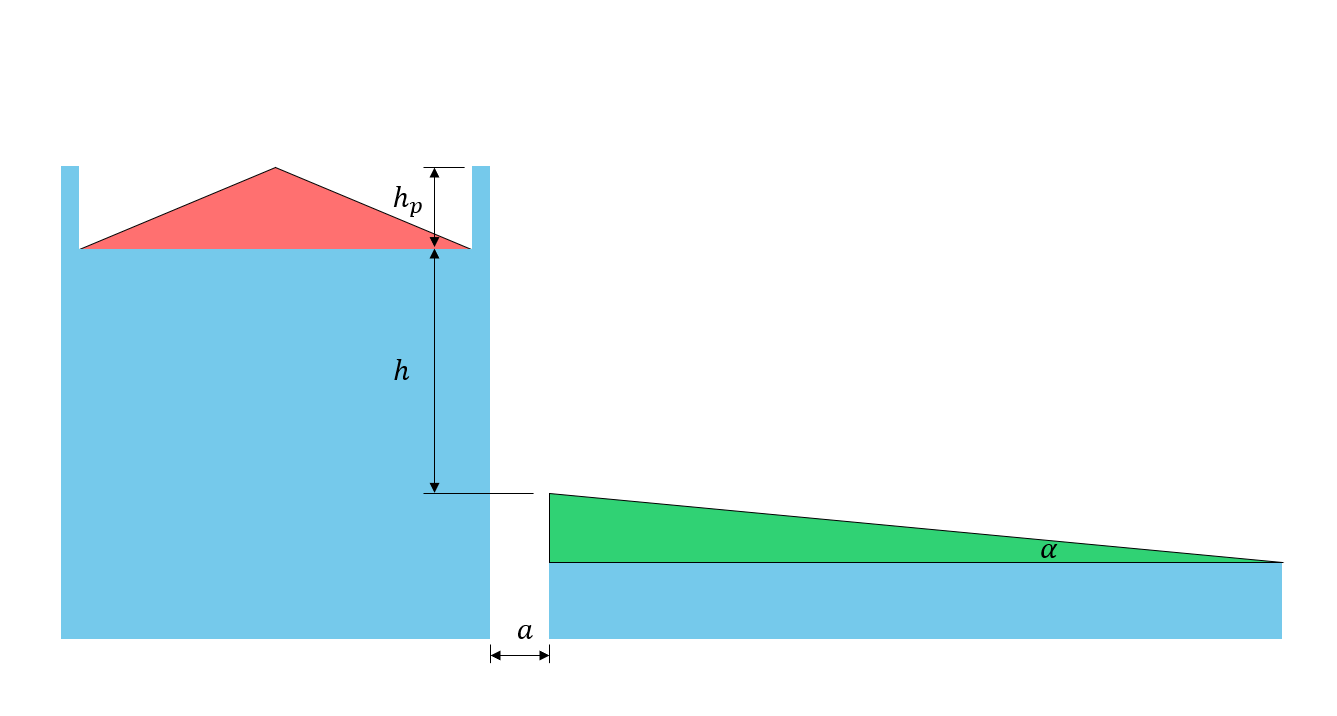
figura 5: Illustrazione dei parametri dimensionali del tetto
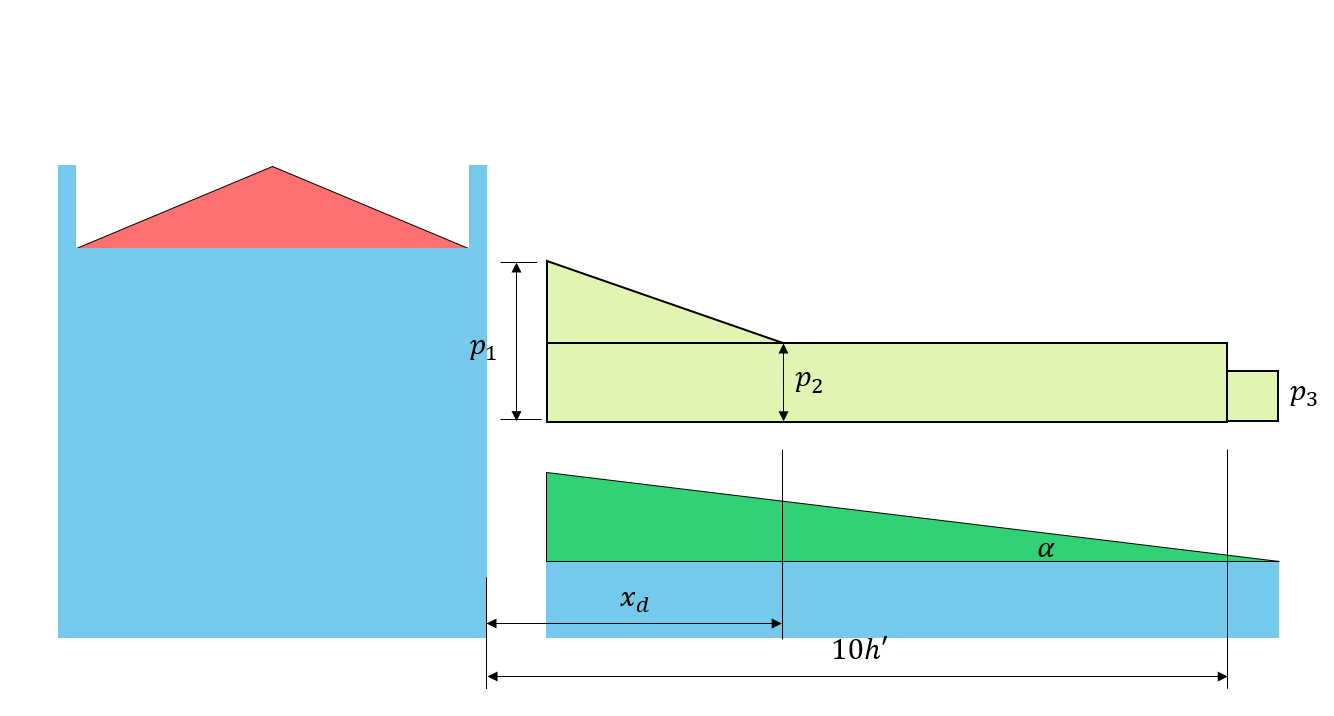
figura 6: Carico di deriva corrispondente sul tetto inferiore basato su Figura 4.1.6.5-A.
\({C}_{a0}\) e \({x}_{d}\) può essere calcolato utilizzando le seguenti formule:
\({C}_{a0} = frac{βγh}{{C}_{b}{S}_{S}}\) o \({C}_{a0} = frac{F}{{C}_{b}}\) (5), qualunque sia minore
\({x}_{d} = 5 \frac{{C}_{b}{S}_{S}}{c}({C}_{a0} – 1)\) (6)
\(F = 0.35β\sqrt{\frac{c({l}_{cs} – 5{{h}_{p}}^{'})}{{S}_{S}}} +{C}_{b}\) ma \(F ≤ 5\) per \({C}_{ws} = 1.0\) (7)
\({h}^{'} = h – \frac{{C}_{b}{C}_{w}{S}_{S}}{c}\) (8)
\({{h}_{p}}^{'} ={h}_{p} – \frac{0.8{S}_{S}}{c}\) ma \(0 ≤ {{h}_{p}}^{'} ≤ \frac{{l}_{cs}}{5}\) (9)
Dove:
\({h}_{p}\) = altezza del parapetto sul tetto superiore (0 in questo caso non essendo presente il parapetto)
\(h ) = differenza di altezza tra il livello del tetto superiore e inferiore
\({C}_{ws}\) = valore di \({C}_{w}\) applicabile alla fonte della deriva
\({l}_{cs}\) = lunghezza caratteristica dell'area sorgente definita come: \(2{w}_{S} -{{w}_{S}}^{2}/{l}_{S}\)
\({l}_{S}\) = dimensione in pianta maggiore dell'area di origine come mostrato in figura 7 e 8, mostrato sotto
\({w}_{S}\) = dimensione in pianta più piccola dell'area di origine come mostrato in Figura 7 e 8, mostrato sotto
\(β\) = 1.0 per il caso I, e 0.67 per i casi II e III.
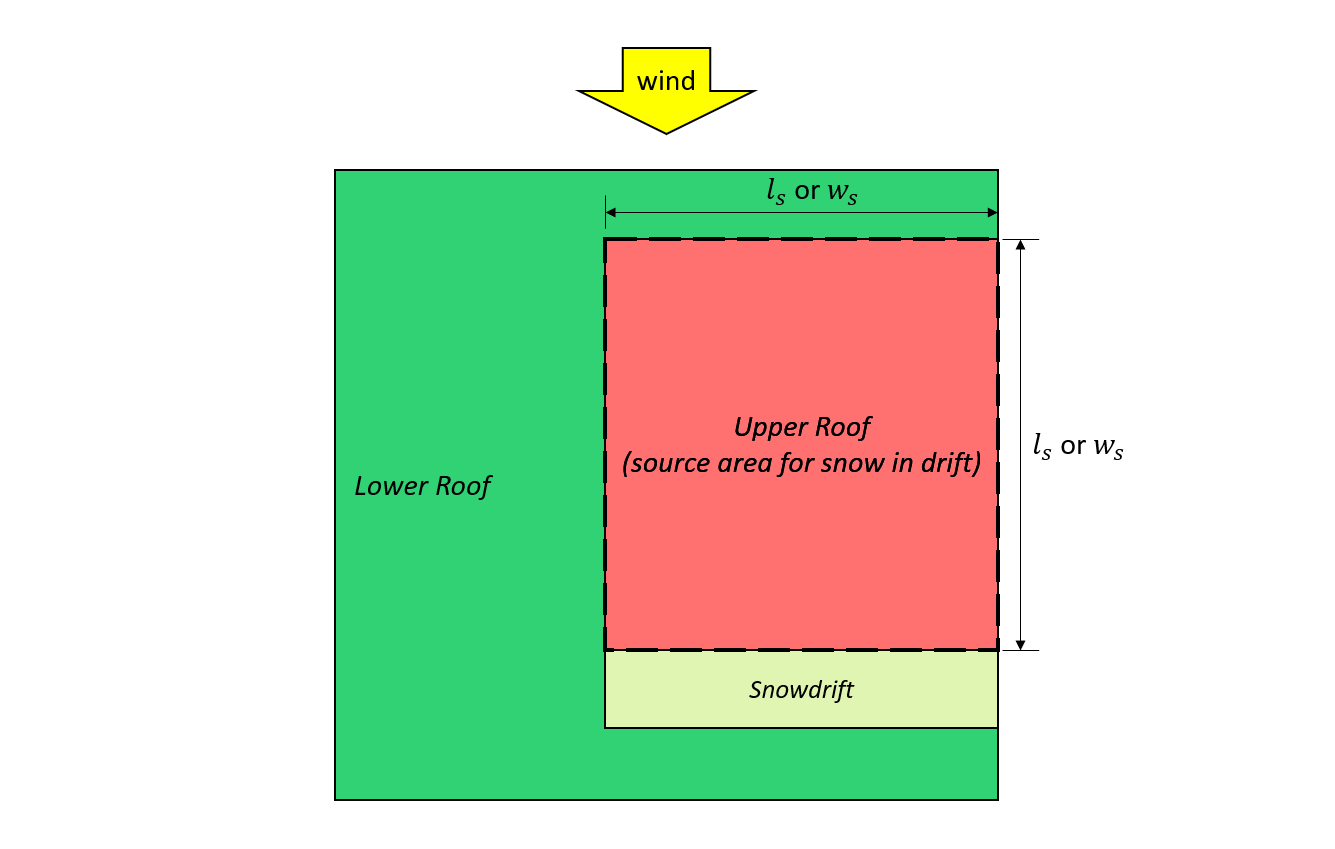
figura 7: Caso I. – cumulo di neve formato dal vento proveniente dal tetto superiore in base Figura 4.1.6.5-B.
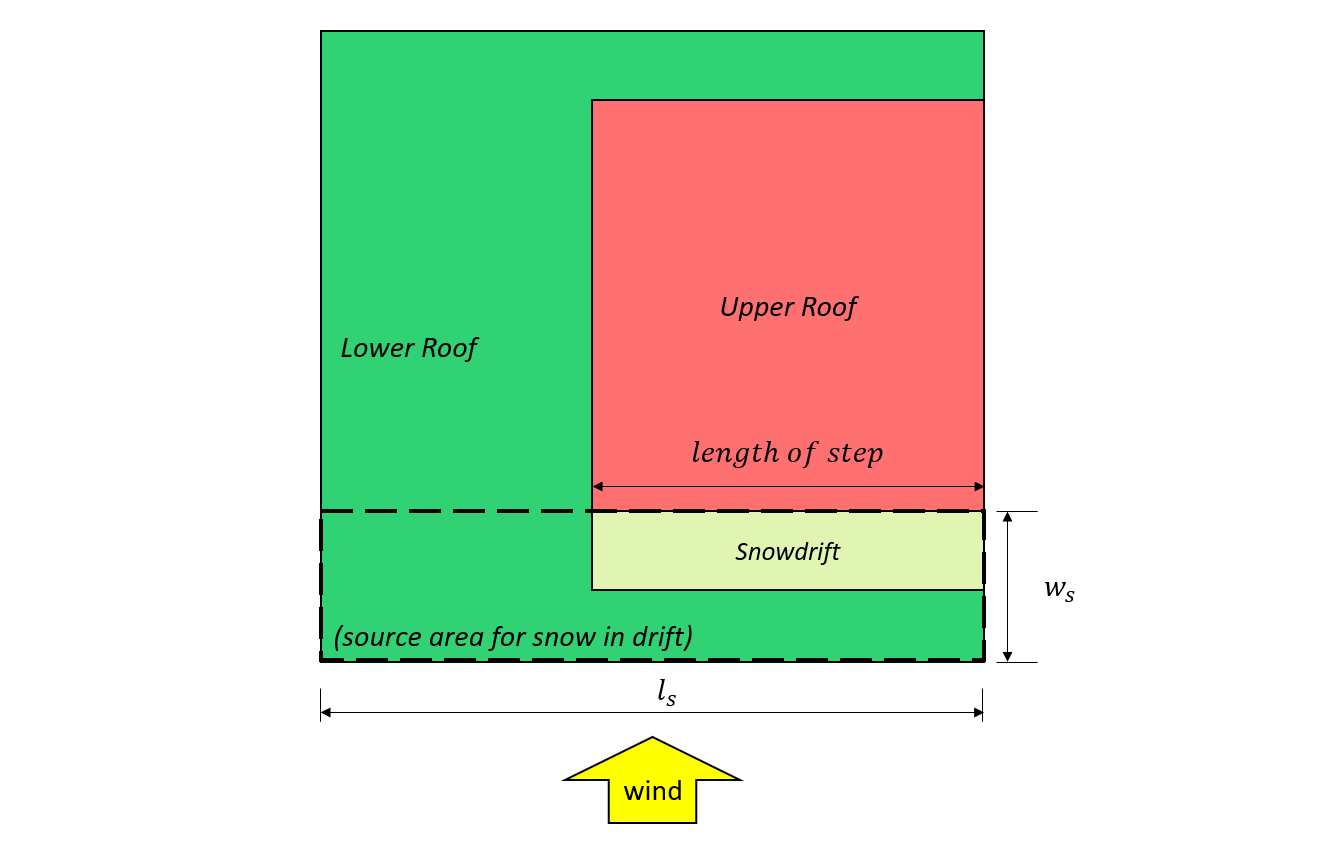
figura 8: Caso II – cumulo di neve formato dal vento proveniente dal tetto inferiore in base Figura 4.1.6.5-B.
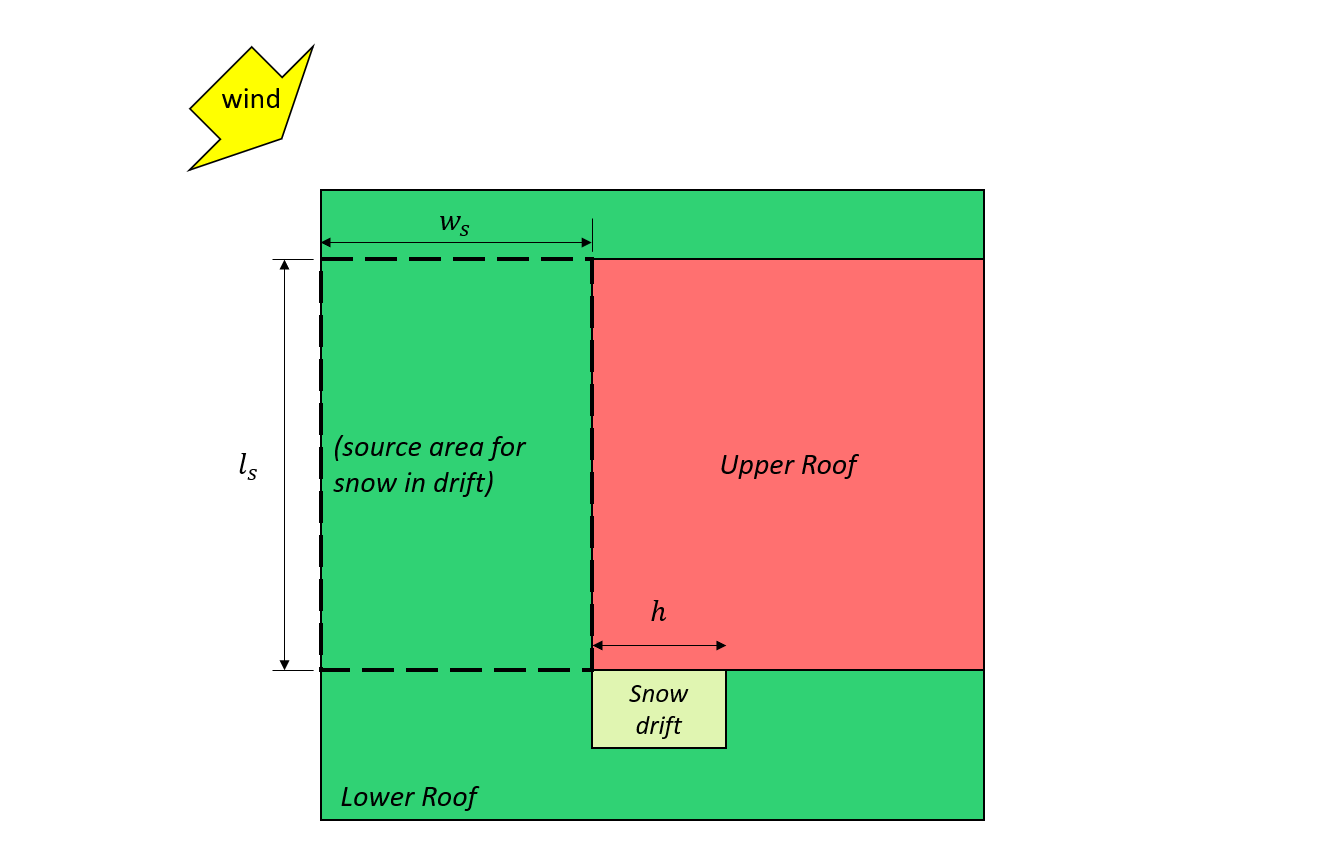
figura 7: Caso III – cumulo di neve parziale formato dal vento proveniente dal tetto inferiore in base Figura 4.1.6.5-B.
Per questo esempio, Verranno presi in considerazione i casi I e II.
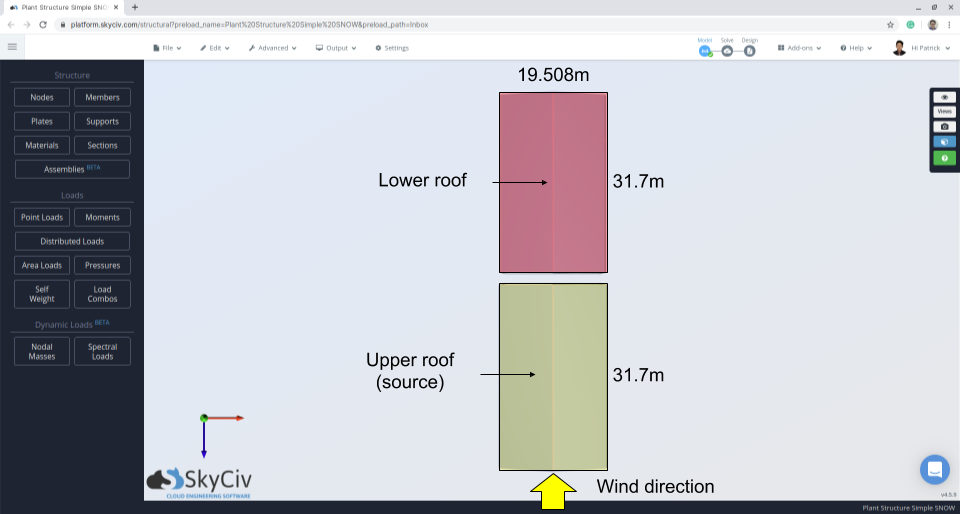
figura 10: Pianta della struttura indicante la direzione del vento e la zona di origine.
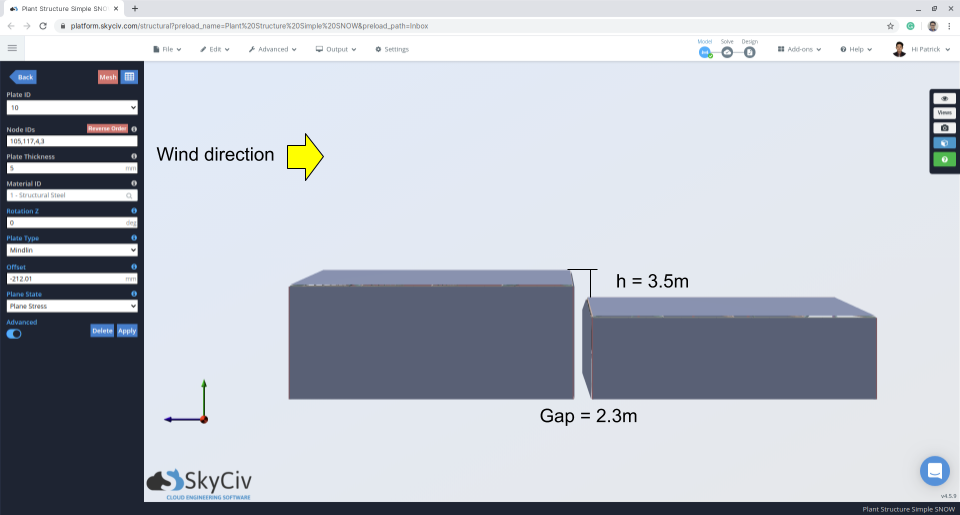
figura 11: Vista in elevazione che indica la distanza e la differenza tra il tetto superiore e inferiore.
Per il caso sbilanciato / spostato parallelo al colmo, \({C}_{un carico}\) sarà calcolato per il caso I e il caso II in base a 4.1.6.5 per il tetto a più livelli. Per il caso I, questi parametri seguenti devono essere prima calcolati utilizzando le varie equazioni menzionate in precedenza in questo esempio:
\(β = 1.0\)
\({h}^{'} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 M)
\({h}_{p} = 0\)
\({{h}_{p}}^{'} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 M)
\(F = 0.35(1.0)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) o \({C}_{a0} = frac{3.66}{0.8} = 4.544\)
\({C}_{a0} = 4.544\)
\({x}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 M)
Da questi parametri, il fattore di accumulo, \({C}_{un carico}\), può essere calcolato sostituendo il valore di \({C}_{a0}\) a ciascuno \(X) distanza. Prendi nota che dobbiamo calcolare \({C}_{un carico}\) a \(x = a\) dove \(a\) è lo spazio tra il tetto poiché lo spazio tra il tetto è inferiore a 5 m come specificato in 4.1.6.6.
a \(x = 0\): \({C}_{un carico} = 4,544 – (4.544 – 1)(0/5.835) = 4.544\)
a \(x = a\): \({C}_{un carico} = 4,544 – (4.544 – 1)(2.3/5.835) = 3.147\)
a \(x = {x}_{d}\): \({C}_{un carico} =1.0\)
a \(x = 10{h}^{'}\): \({C}_{un carico} =1.0\)
l l l, \({C}_{S} = 1.0\). Inoltre, quando si trova il carico di neve specificato sul tetto superiore, il fattore di accumulo, \({C}_{un carico}\), e fattore di pendenza, \({C}_{S}\), sono entrambi uguali a 1.0. Quindi, l'entità dei carichi di neve specificati in ciascuna posizione sono:
a \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa)
a \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
a \(x = {x}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
a livello del tetto superiore: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa)
Vento che agisce parallelamente alla cresta – Caso II – Vento dal tetto inferiore a quello superiore
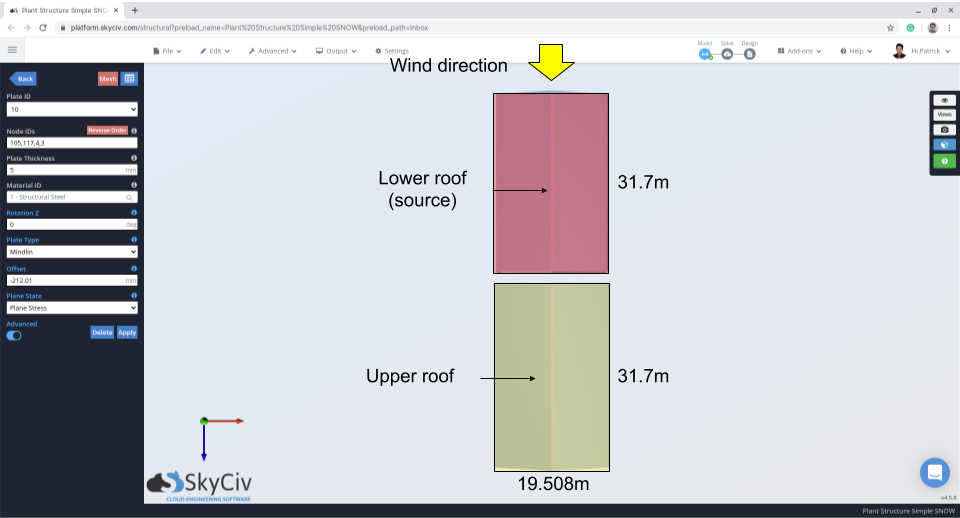
figura 12: Pianta della struttura indicante la direzione del vento e la zona di origine – vento dal tetto inferiore a quello superiore.
Per il caso II, il calcolo è simile al caso I ma ha una differenza \(β = 0.67\):
\(β = 0.67\)
\({h}^{'} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 M)
\({h}_{p} = 0\)
\({{h}_{p}}^{'} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 M)
\(F = 0.35(0.67)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({C}_{a0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) o \({C}_{a0} = frac{2.70}{0.8} = 3.375\)
\({C}_{a0} = 3.375\)
\({x}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 M)
a \(x = 0\): \({C}_{un carico} = 3,375 – (3.375 – 1)(0/3.909) = 3.375\)
a \(x = a\): \({C}_{un carico} = 3,375 – (3.375 – 1)(2.3/3.909) = 1.978\)
a \(x = {x}_{d}\): \({C}_{un carico} =1.0\)
a \(x = 10{h}^{'}\): \({C}_{un carico} =1.0\)
a \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa)
a \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
a \(x = {x}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
a livello del tetto superiore: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa)
Per l'illustrazione, il corrispondente \({p}_{1}\), \({p}_{2}\), e \({p}_{3}\) sono mostrati nelle figure 13 e 14 di seguito per entrambi i casi I e II, rispettivamente.
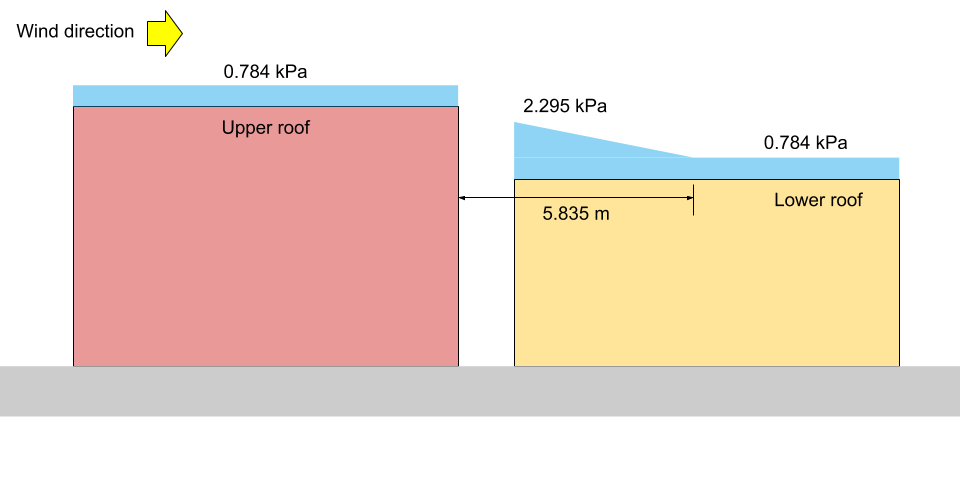
figura 13: Illustrazione del carico di neve per il caso I (non in scala).
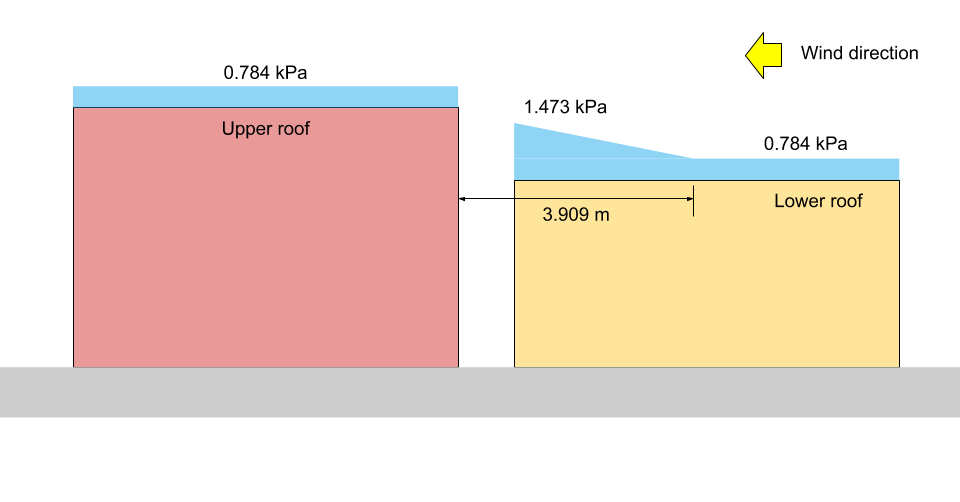
figura 14: Illustrazione del carico di neve per il caso II (non in scala).
Completa questi calcoli automaticamente in pochi minuti
È stato un lungo calcolo, cosa puoi fare come ingegnere per accelerare questo processo per i tuoi progetti futuri? Recentemente SkyCiv ha rilasciato e automatizzato Snow Load Generator come parte di SkyCiv Load Generator, che può anche generare carichi di vento. Per trovare i carichi di neve dell'esempio mostrato, bastano pochi clic utilizzando lo strumento:
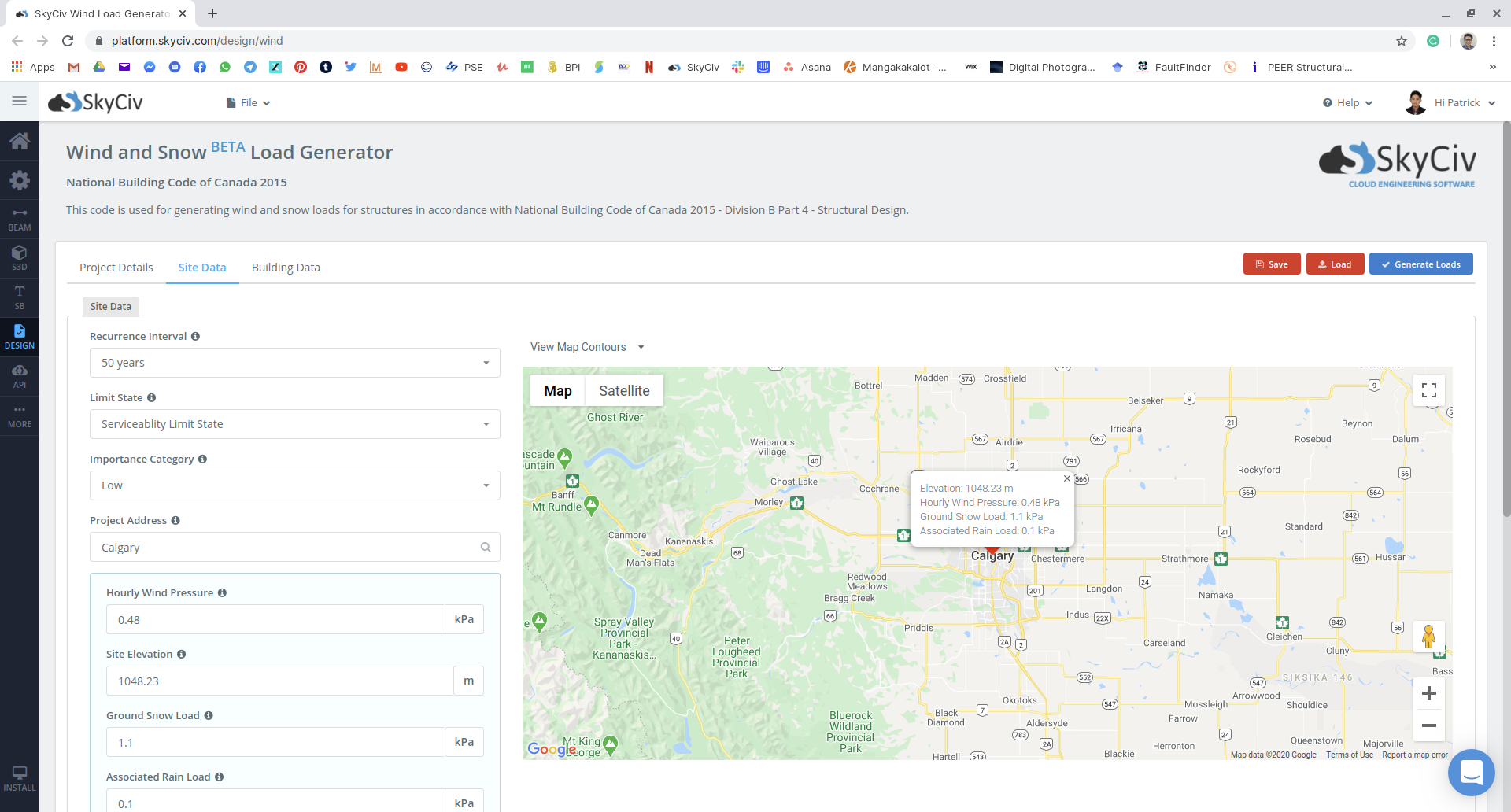
figura 15: Inserimento dei dati del sito sul modulo SkyCiv Load Generator utilizzando il nostro esempio.
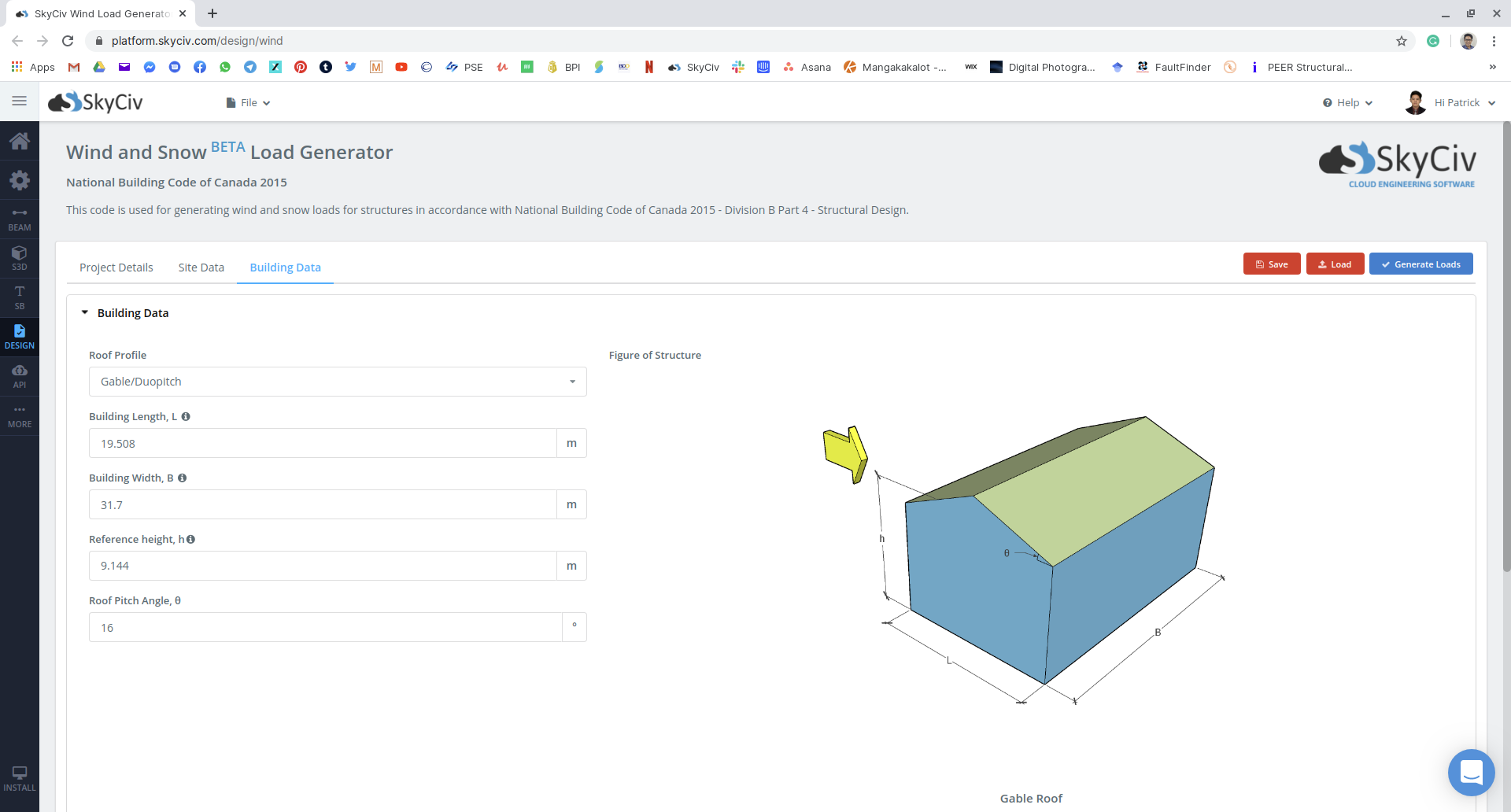
figura 16: Inserimento dei parametri di costruzione e neve sul modulo SkyCiv Load Generator utilizzando il nostro esempio.
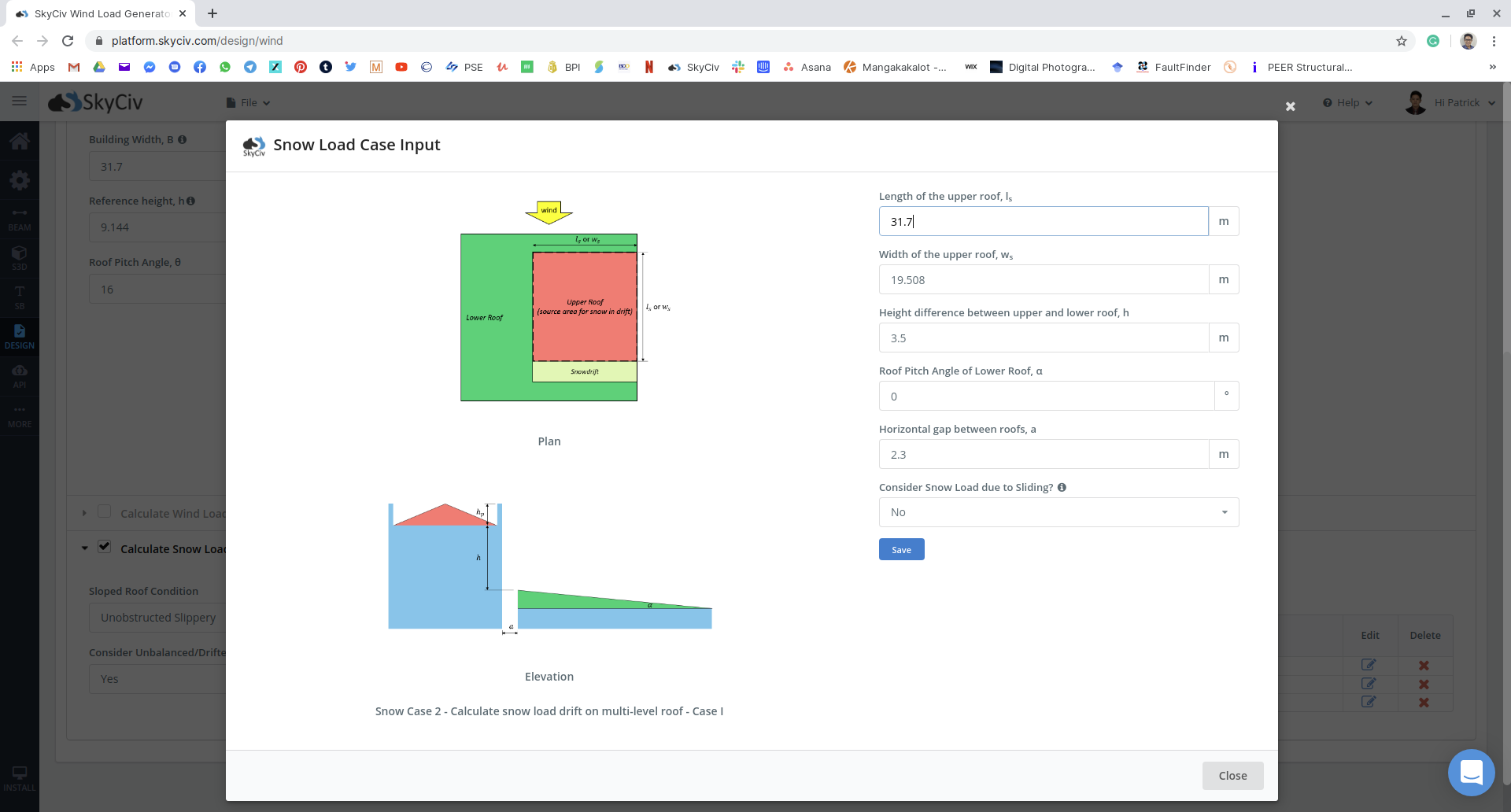
figura 17: Input del carico di neve per più casi sbilanciati per l'esempio.
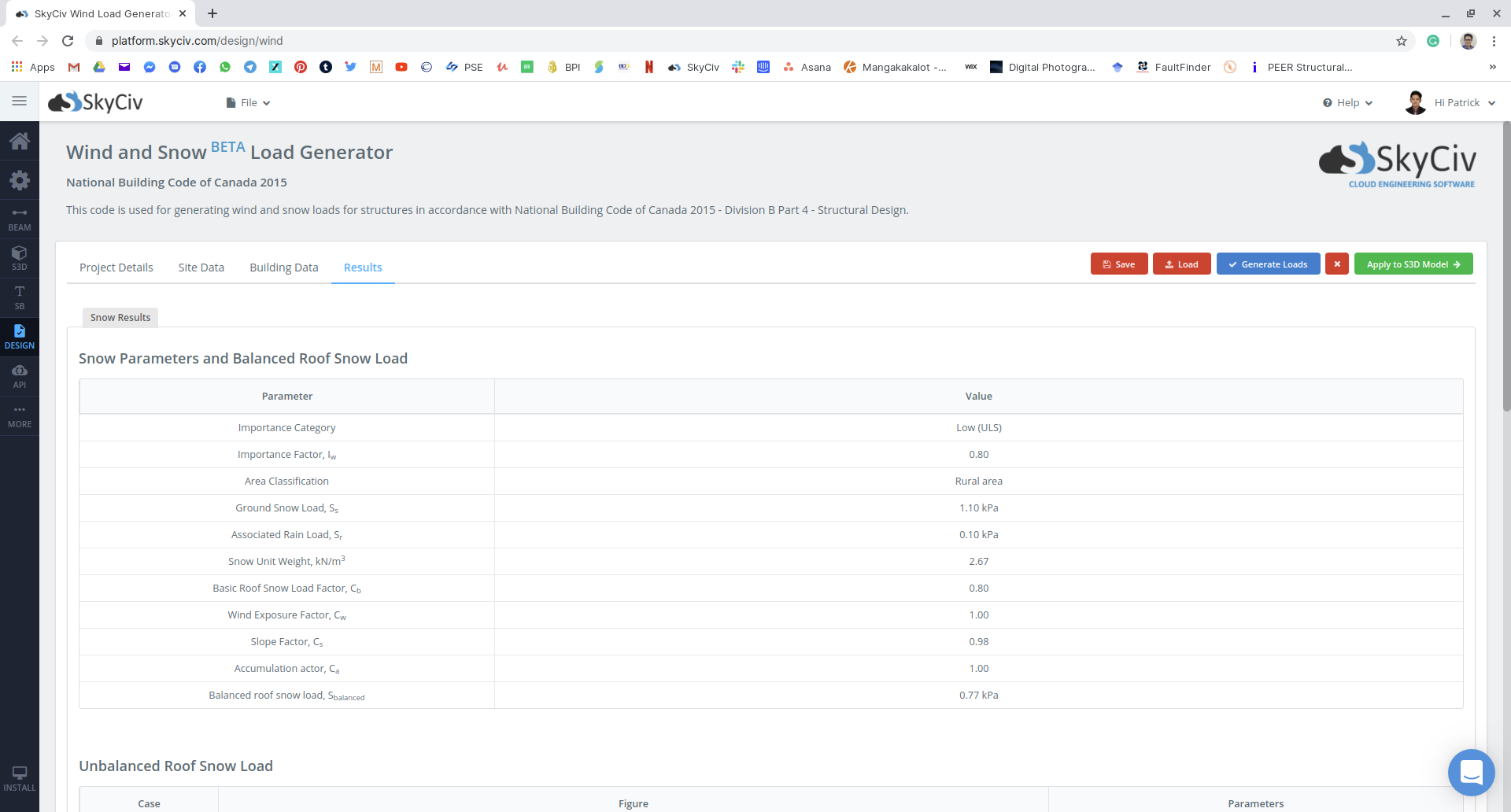
figura 18: Riepilogo dei parametri di carico della neve utilizzati e del carico di neve bilanciato da applicare alla struttura.
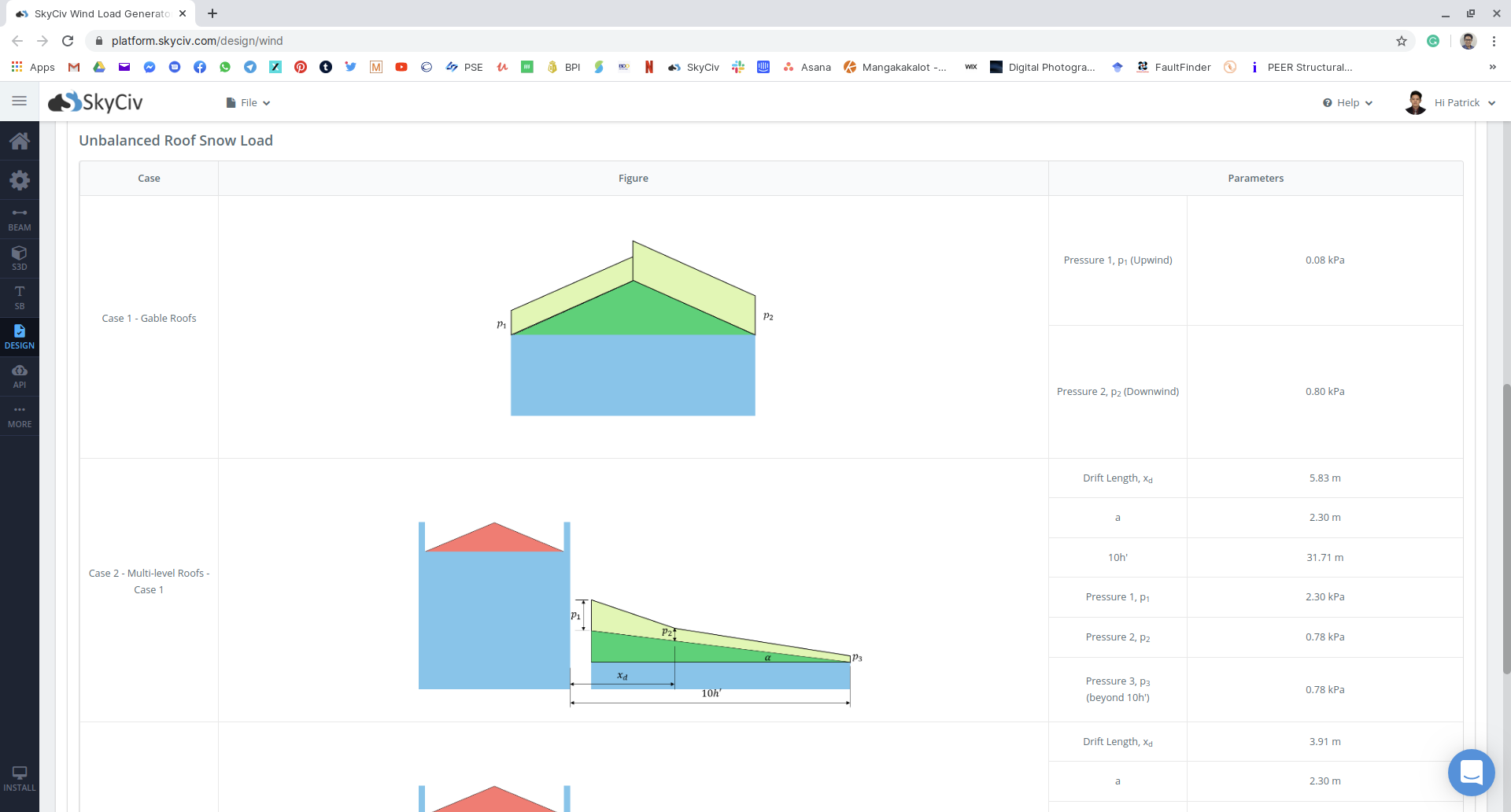
figura 19: Riepilogo dei risultati del carico di neve sbilanciato.
I calcoli del carico di neve nel modulo SkyCiv Load Generator sono supportati da codici di riferimento come ASCE 7-10, 7-16, NEL 1991-1-3, NBCC 2015, e AS / NZS 1170.3, ed è disponibile su Indipendente, autonomo (Solo generatore di carico) e Professionale conti. Familiarità con la programmazione e le API? Questa funzionalità può essere automatizzata con l'uso di API SkyCiv.
Ingegnere strutturale, Sviluppo del prodotto
MS Ingegneria Civile
Riferimenti:
- Consiglio nazionale delle ricerche del Canada. (2015). National Building Code of Canada, 2015. Consiglio nazionale delle ricerche del Canada.
Nota:
- Riferimento del codice NBCC per “Fattore di carico di base della neve sul tetto” — cercare 4.1.6.2 Frase (2)
- Riferimento del codice NBCC per “Fattore di esposizione al vento” — cercare 4.1.6.2 Frasi (3) e (4)
- Riferimento del codice NBCC per “Fattore di pendenza” — cercare 4.1.6.2 Frasi (5), (6), e (7)
- Riferimento del codice NBCC per “Fattore di accumulo” — cercare 4.1.6.2 Frase (8), 4.1.6.5 per tetti a più livelli, 4.1.6.6 per tetti con intercapedine, e 4.1.6.9 per tetti a due falde


