Tabella dei contenuti
- Panoramica – Qual è il momento di inerzia
- Esempio – Come calcolare il momento di inerzia
- Formule ed equazioni
- Calcolatrici
- Domande pratiche
Panoramica – Qual è il momento di inerzia?
Nel contesto dell'ingegneria strutturale, il Momento d'Inerzia è una proprietà della sezione utilizzata per determinare la capacità di un elemento strutturale di resistere alle forze di flessione e torsione. Di solito è un buon indicatore della rigidità e della resistenza delle sezioni sotto carico. Un momento di inerzia più elevato significa che la struttura è meglio attrezzata per resistere alla flessione e alla deflessione, rendendolo un fattore essenziale nella progettazione delle travi, colonne, e altri componenti portanti. Nota: A volte questo viene erroneamente definito come secondo momento di inerzia, tuttavia non è corretto. Gli altri nomi per Momento di Inerzia sono: momento d'inerzia dell'area, o secondo momento di la zona.
Esempio – Come calcolare il momento di inerzia di una sezione della trave
Prima di trovare il momento di inerzia di una sezione della trave (noto anche come secondo momento di area di una sezione della trave), il suo centroide (o centro di massa) deve essere noto. Ad esempio, se fosse stato richiesto il momento di inerzia della sezione attorno al suo asse orizzontale (XX) sarebbe stato necessario conoscere (y) prima il centroide verticale (Si prega di visualizzare i nostri tutorial sul calcolo del centroide di una sezione della trave e calcolo del primo momento/statico dell'area).
Prima di iniziare, se stavate cercando il nostro Calcolatore gratuito del momento d’inerzia cliccate sul link per saperne di più. Questo calcolerà il centroide, il momento di inerzia, e altri risultati e ti mostrerà anche i calcoli! Ma per ora, diamo un'occhiata a una guida passo-passo e un esempio di come calcolare il momento di inerzia:
Step 1: Segmentare la sezione della trave in parti
Nel calcolo del momento di inerzia di area, dobbiamo calcolare il momento di inerzia dei segmenti più piccoli. Prova a suddividerli in semplici sezioni rettangolari. Ad esempio, considera la sezione della trave a I qui sotto, presente anche nel nostro tutorial sui centroidi. Abbiamo scelto di dividere questa sezione in 3 segmenti rettangolari:
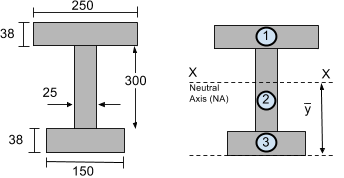
Step 2: Calcola l'asse neutro (NA)
L'asse neutro (NA) o l'asse orizzontale XX si trova al centroide o al centro della massa. Nel nostro tutorial sui centroidi, il centroide di questa sezione è stato precedentemente trovato a 216.29 mm dal fondo della sezione – puoi trovarlo nel come trovare il baricentro di una forma tutorial. Questo può anche essere calcolato dal nostro calcolatore del centroide o da equazioni centroidi .
Calcolo del baricentro, o Asse Neutro, è essenziale in come calcolare il momento d'inerzia di una trave, poiché questo è l'asse su cui agisce il momento di inerzia.
Step 3: Calcola il Momento d'inerzia
Per calcolare il momento di inerzia totale della sezione dobbiamo usare “teorema parallelo dell'asse”:

Poiché l'abbiamo diviso in tre parti rettangolari, dobbiamo calcolare il momento di inerzia di ciascuna di queste sezioni. È ampiamente noto che l'equazione del momento di inerzia di un rettangolo attorno al suo asse centroide è semplicemente:
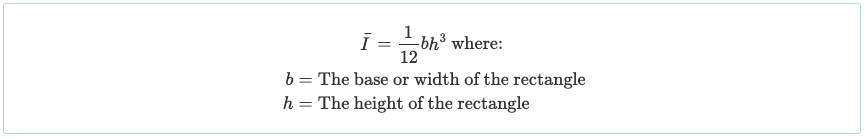
Il momento di inerzia di altre forme è spesso indicato nella parte anteriore/ posteriore dei libri di testo o da questa guida in momento di inerzia delle forme. Tuttavia, la forma rettangolare è molto comune per le sezioni della trave, quindi vale la pena memorizzare.
Ora abbiamo tutte le informazioni necessarie per usare il “teorema parallelo dell'asse” e trovare il momento totale di inerzia della sezione della trave a I. Nel nostro esempio del momento di inerzia:

Ecco la nostra guida per calcolare l'area del momento per le sezioni della trave. Questo risultato è fondamentale nell'ingegneria strutturale ed è un fattore importante nella deflessione di una trave. Speriamo che il tutorial ti sia piaciuto e non vediamo l'ora di ricevere i tuoi commenti. Per maggiori informazioni, visita il nostro tutorial su Formula ed equazioni del momento d'inerzia.
Formule ed equazioni
Ogni tipo di sezione (rettangolare, I Beam, Circolare) ha una propria formula per un calcolo rapido. Si tratta di equazioni semplificate che consentono agli ingegneri di calcolare rapidamente e facilmente questa importante proprietà.
Le equazioni sono un'espressione semplificata dei passaggi precedenti. Per esempio, la formula per il momento di inerzia di un rettangolo cavo è fondamentalmente il MOI della sezione più grande – il più piccolo (interno) sezione:

[matematica] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [matematica]
SkyCiv ha messo insieme una risorsa utile per il comune Formula del momento d'inerzia.
Calcolatrici
Ci sono molti modi per calcolare il momento di inerzia, uno dei quali è quello di utilizzare il software per rendere il processo più facile.
Il Generatore di Sezioni SkyCiv è uno strumento di progettazione di sezioni completo che va ben oltre il calcolo del momento di inerzia. Ti mostrerà anche i calcoli passo passo su come trovare il momento di inerzia:
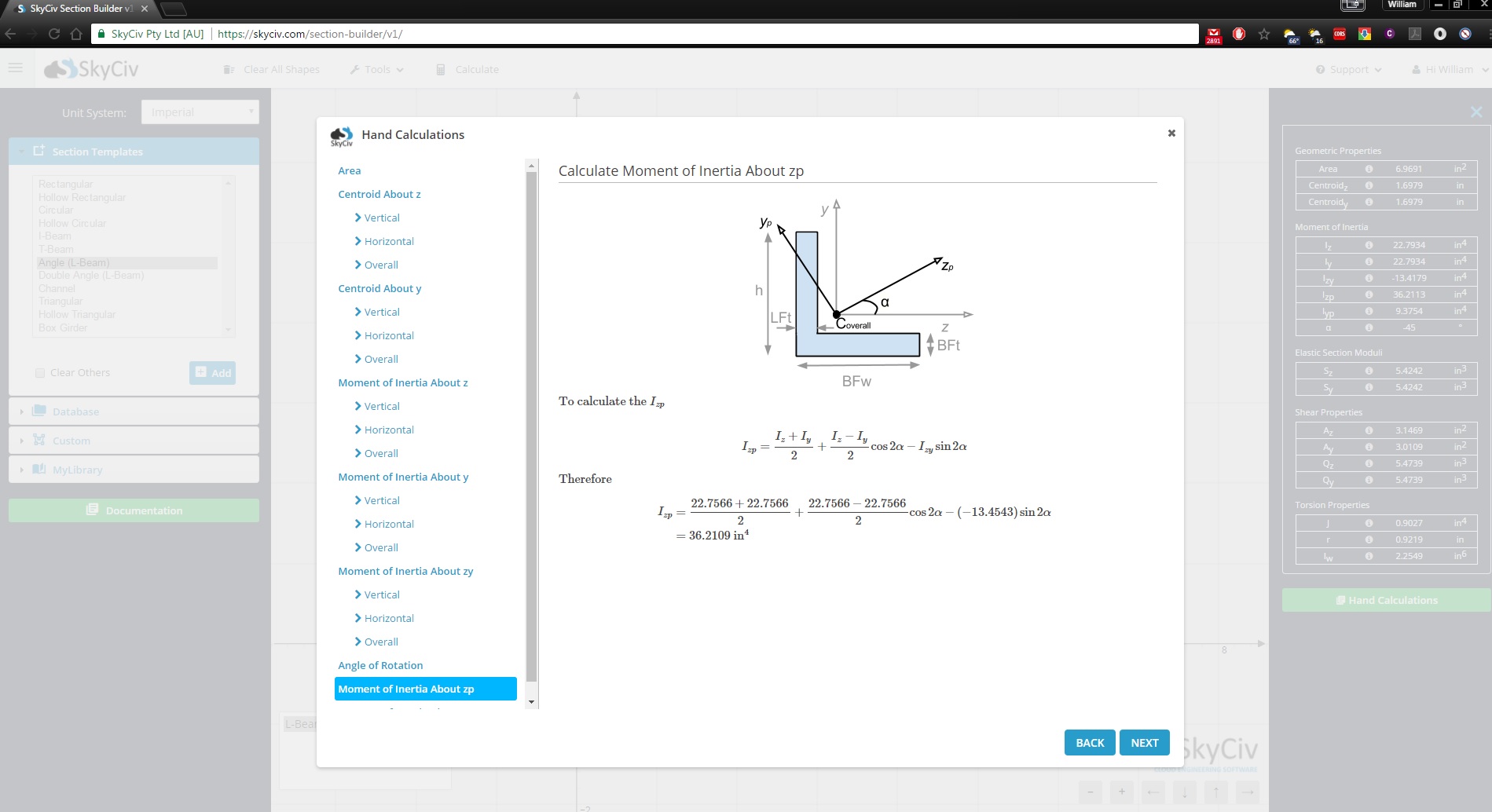
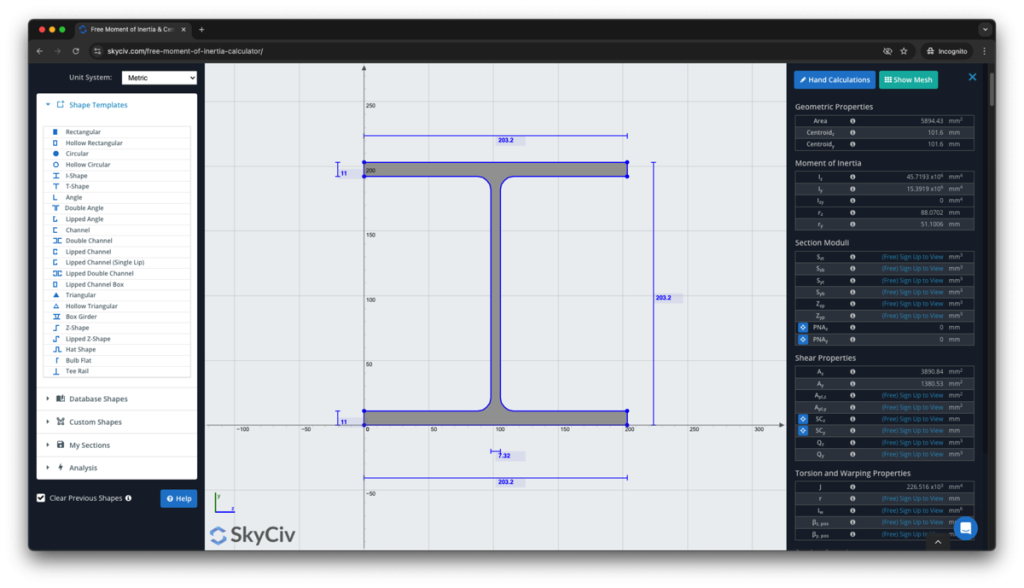
Iscriviti oggi per scoprire di più sul software SkyCiv, o prenota una DEMO GRATUITA per ricevere assistenza sui tuoi progetti di ingegneria per gli utenti iscritti!
Inoltre, SkyCiv ha una versione gratuita Calcolatore delle proprietà della sezione come parte della libreria Quick Design. È uno strumento semplificato, ma calcolerà anche il momento di inerzia delle forme di sezione comuni.
Domande pratiche
Domanda 1: Sezione rettangolare
Problema: Calcolare il momento d'inerzia (Ixx e Iyy) per una sezione rettangolare con una larghezza (b) di 200 mm e un'altezza (h) di 300 mm.
Soluzione: Le formule per il momento di inerzia di un rettangolo sono:
Sostituendo i valori dati:
- b=200 mm
- h=300 mm
Per Ixx:
Per Iyy:
Domanda 2: I-Beam
Problema: Calcolare il momento d'inerzia dell'asse maggiore (Ixx) di una sezione di trave a I con le seguenti dimensioni:
- Larghezza della flangia superiore (TFW) = 6 pollici
- Spessore della flangia superiore (Tft) = 0.43 pollici
- Profondità della sezione = 6 pollici
- Spessore del nastro (wt) = 0.29 pollici
- Larghezza della flangia inferiore (BFW) = 6 pollici
- Spessore della flangia inferiore (Bft) = 0.43 pollici
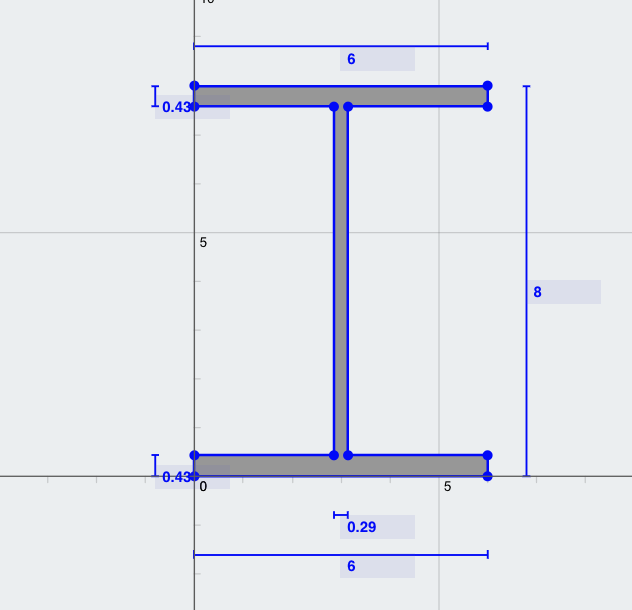
Soluzione:

