Un esempio completamente funzionante di montaggio a terra Calcolo del carico del vento del pannello solare e della pressione della neve utilizzando ASCE 7-16
Con le recenti tendenze nell'uso delle energie rinnovabili per arginare gli effetti del cambiamento climatico, una delle industrie in rapida crescita come soluzione a questo problema è l'uso dell'energia solare. Inoltre, una delle industrie in rapida crescita come soluzione a questo problema è l'uso dell'energia solare. In effetti, le installazioni di pannelli solari sui tetti delle case e la costruzione di parchi solari che utilizzano pannelli solari montati a terra aumentano di numero. La necessità di calcolare il carico del vento sui pannelli solari e la pressione della neve è fondamentale affinché questi raggiungano la durata. In questo articolo, discuteremo come calcolare i carichi di neve e vento sui pannelli solari montati a terra utilizzando ASCE 7-16.
SkyCiv automatizza i calcoli della velocità del vento con pochi parametri. Prova il nostro Calcolatore del carico del vento del pannello solare
Dati della struttura
In questo esempio, utilizzeremo i seguenti dati:
tavolo 1. Dati di costruzione necessari per il nostro calcolo del carico di vento e neve.
| Posizione | 395 Rocky Point Road, Cordova, Memphis, Tennessee |
| occupazione | miscellaneo – pannello solare |
| Terreno | Terreno agricolo pianeggiante |
| Larghezza pannello | 16.25 ft |
| Larghezza pannello | 13.33 ft |
| Larghezza pannello | 8.33 ft |
| Larghezza pannello | 30° |
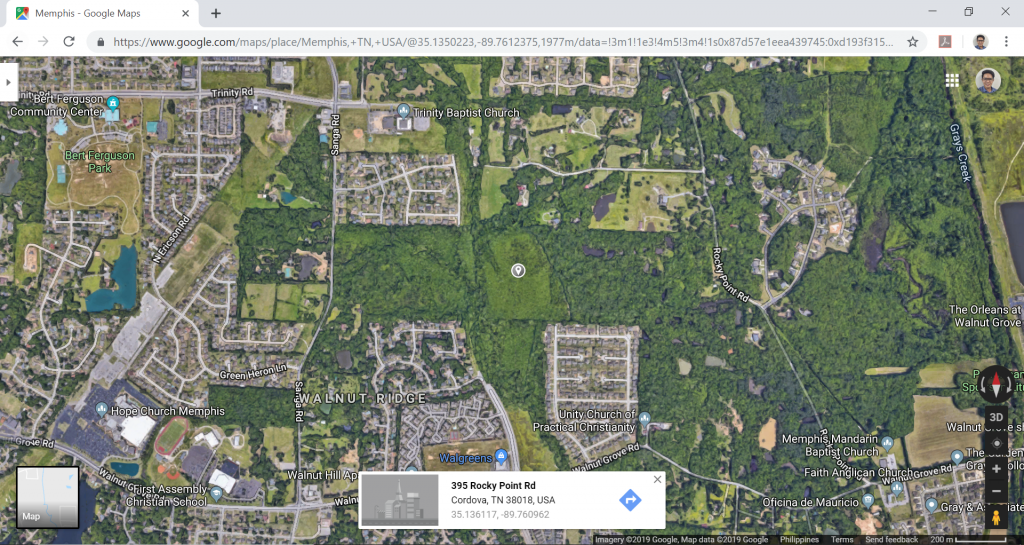
figura 1. Posizione del luogo (da Google Maps).
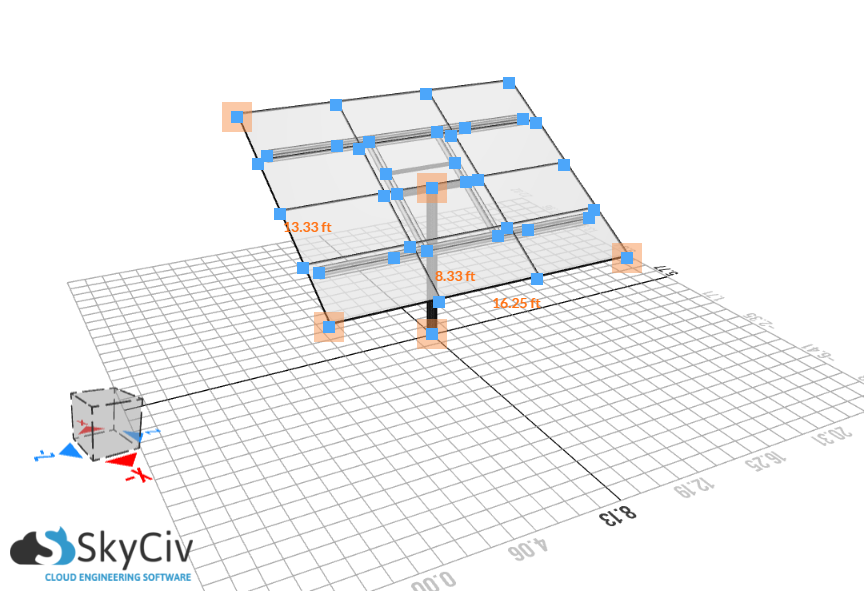
figura 2. Larghezza pannello.
Caricamento del vento
Nel calcolo del carico del vento sui pannelli solari, useremo l'ASCE 7-16 Capitolo 27 – Carico del vento – considereremo il pannello solare a terra come un edificio a monopendenza aperta quando l'angolo di inclinazione è inferiore o uguale a 45° e come un segno solido per un angolo di inclinazione maggiore di 45°. Considereremo il pannello solare a terra come un edificio aperto con copertura monopendenza quando l'angolo di inclinazione è inferiore o uguale a 45° e come un segno solido per un angolo di inclinazione maggiore di 45°.
La formula per determinare le pressioni del vento di progetto è la seguente:
Per angolo di inclinazione ≤ 45° (considerato un edificio aperto con copertura monopendenza):
\(p = {q}_{h}G{C}_{N}\) (1)
Per angolo di inclinazione > 45° (considerato segno solido):
\(p = {q}_{h}G{C}_{f}\) (2)
Dove:
\(G\) = fattore di effetto raffica
\({C}_{N}\) = coefficiente di forza netta per copertura monopendenza aperta
\({C}_{f}\) = coefficiente di forza netto per i segni solidi
\({q}_{h}\) = pressione di velocità all'altezza di riferimento, \(h\), in psf, dato dalla formula:
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\) (3)
\({K}_{z}\) = coefficiente di pressione della velocità
\({K}_{zt}\)= fattore topografico
\({K}_{d}\) = fattore di direzionalità del vento
\({K}_{e}\) = fattore di elevazione del suolo
\(V \) = velocità del vento di base in mph
Prendi nota che per l'angolo di inclinazione > 45°, noi le dimensioni da utilizzare sono la proiezione verticale del pannello solare e quindi utilizziamo la formula per i coefficienti di forza netti per i segni solidi. Ci immergeremo in profondità nei dettagli di ciascun parametro di seguito.
Categoria di rischio
Il primo passo è determinare la Categoria di Rischio del pannello solare in base all'uso o all'occupazione. Dalla tabella 1.5-1 dell'ASCE 7-16, possiamo classificare il pannello solare montato a terra in questo esempio nella categoria di rischio I.
Velocità del vento di base, \(V\)
The ASCE 7-16 fornisce una mappa del vento in cui la velocità del vento di base corrispondente di una posizione può essere ottenuta dalle figure da 26.5-1A a 1C. Dalla Figura 26.5-1A, Cordova, Memphis, Il Tennessee è in qualche modo vicino al punto in cui il punto rosso su Figura 3 sotto, e da lì, la velocità del vento di base, \(V\), è 100 mph. Si noti che il valore di base della velocità del vento è interpolato dai contorni del vento più vicini.
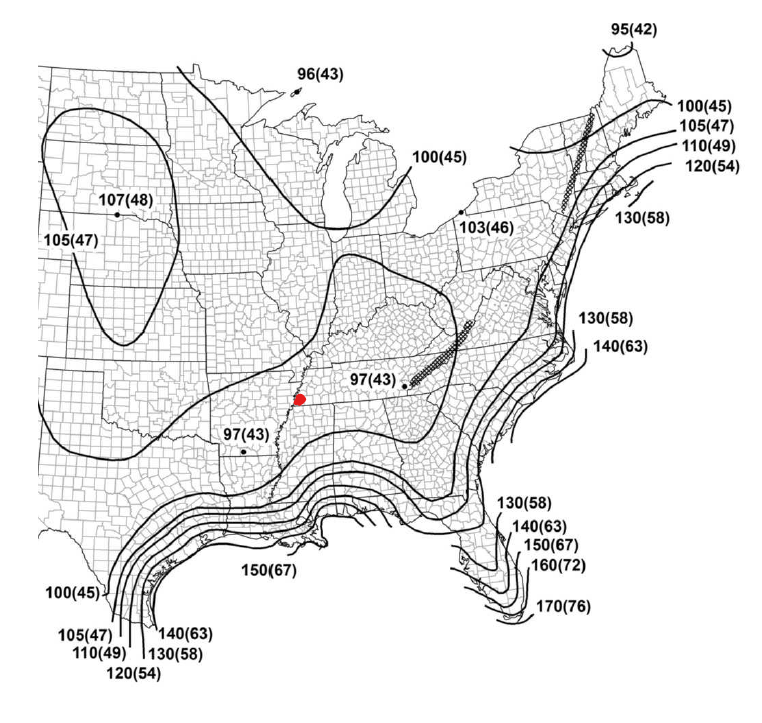
figura 3. Mappa di base della velocità del vento dalla Figura 26.5-1A di ASCE 7-16 (Categoria di rischio I) con punto rosso per indicare la posizione del nostro pannello solare.
SkyCiv automatizza i calcoli della velocità del vento con pochi parametri. Prova il nostro Calcolatore del carico del vento del pannello solare
Categoria di esposizione
A seconda della direzione del vento da analizzare, la categoria di esposizione del pannello solare deve essere determinata dal settore sopravento a 45° in base alla sezione 26.7 dell'ASCE 7-16. Inoltre, La sezione C26.7 fornisce fotografie aeree che mostrano esempi di esposizioni B, C, e D nelle figure da C26.7-5 a C26.7-7.
In questo esempio, utilizzeremo solo vento proveniente da sud. Quindi, sulla base degli esempi di fotografie aeree, possiamo classificare il terreno sopravento all'Esposizione C in base alla Figura C26.7-6(b) o “Terreno aperto con ostacoli sparsi con altezze generalmente inferiori a 30 ft (9.1 m)” come mostrato in figura 4 sotto. Useremo la categoria di esposizione per calcolare il coefficiente di pressione di velocità \({K}_{z}\)span> e/o Fattore topografico \({K}_{zt}\) se necessario.
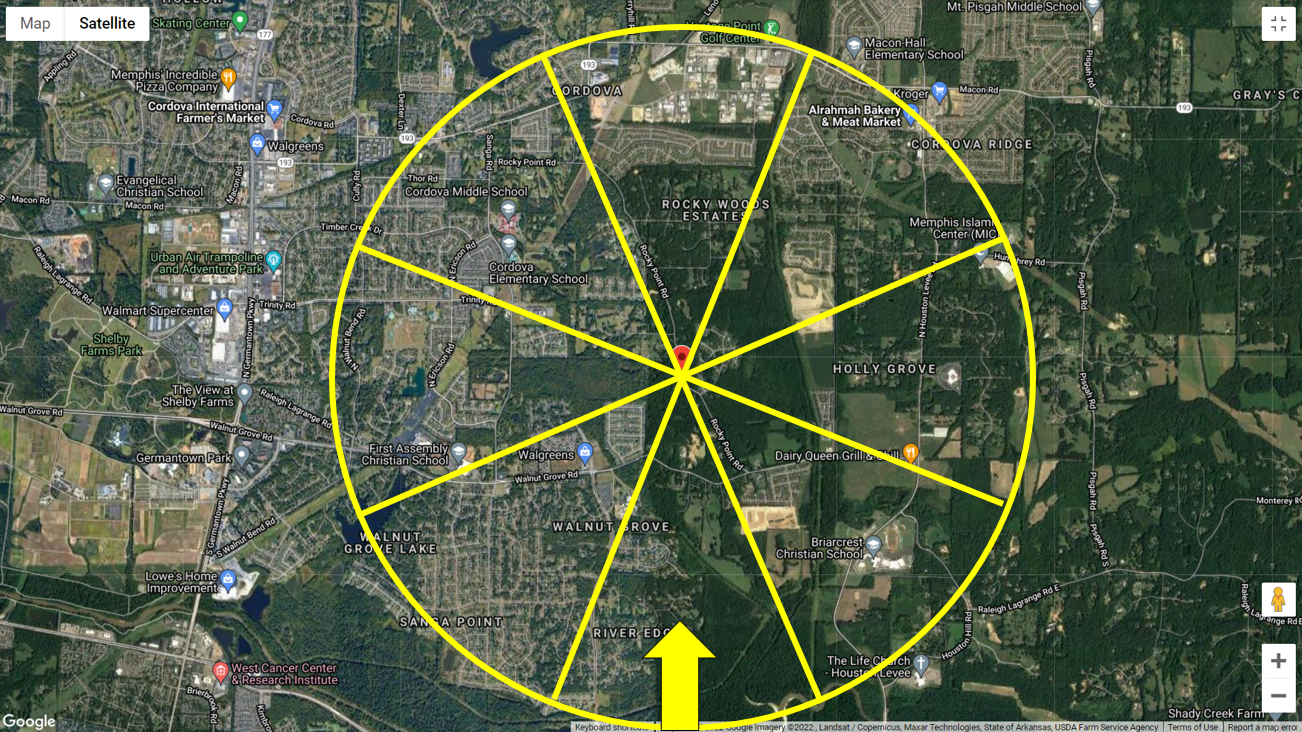
figura 4. Fotografia aerea del terreno con vento proveniente da sud.
Fattore di direzionalità del vento, \( {K}_{d} \)
Il fattore di direzionalità del vento, \({K}_{d} \), per il pannello solare è uguale a 0.85 poiché il pannello solare può essere considerato come MWFRS (asce7) quando l'angolo di inclinazione è inferiore o uguale a 45° e come segno solido per l'angolo di inclinazione maggiore di 45° in base alla tabella 26.6-1 dell'ASCE 7-16.
Fattore di elevazione del suolo, \( {K}_{e} \)
Il fattore di elevazione del suolo, \({K}_{e} \), può essere calcolato utilizzando la tabella 26.9-1 dell'ASCE 7-16. Per questo esempio, poiché l'altezza del sito è uguale a 350.48 ft, \({K}_{e} \) può essere calcolato utilizzando la formula:
\( {K}_{e} = {e}^{-0.0000362{z}_{g}} \) (4)
\( {K}_{e} = {e}^{-0.0000362(350.48)} = 0.987\)
\( {K}_{e} = 0.987 \)
Usando l'equazione (4), \({K}_{e} \) è uguale a 0.987.
Fattore topografico, \( {K}_{zt} \)
I parametri per calcolare il fattore topografico, \({K}_{zt}\), sono dettagliati in Figura 26.8-1 dell'ASCE 7-16. Per determinare se sono necessari ulteriori calcoli del fattore topografico, dobbiamo verificarlo usando la sezione 26.8.1. Se il sito non soddisfa tutte le condizioni elencate, quindi il fattore topografico può essere preso come 1.0. Dalla quota del suolo generata dalle quote di Google, possiamo supporre che il terreno sia Piatto, perciò, \({K}_{zt}\) si può presumere che lo sia 1.0 per vento proveniente da sud.
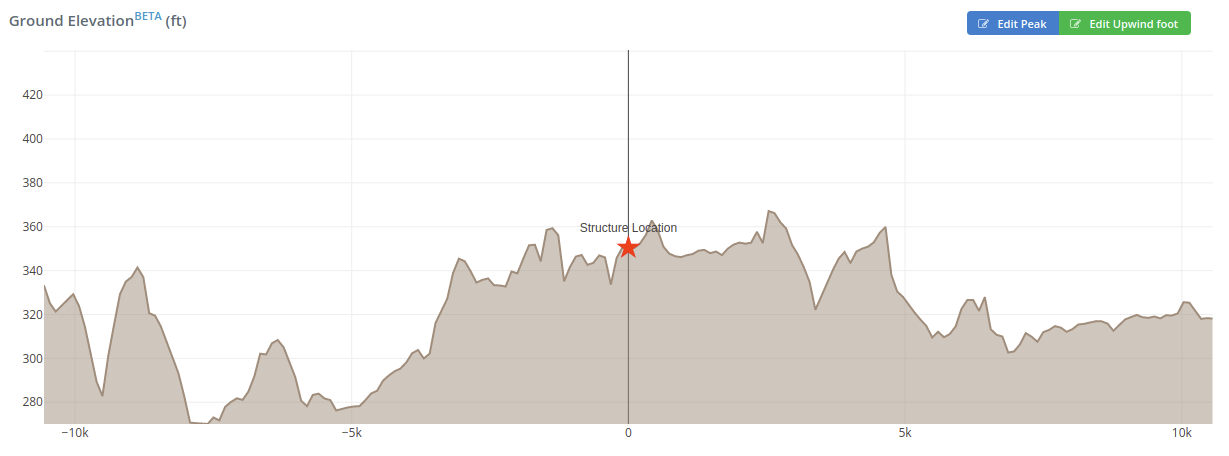
figura 5. Profilo altimetrico del sito in direzione del vento S-N.
Coefficiente di pressione di velocità, \({K}_{z}\)
Il coefficiente di pressione della velocità, \({K}_{z}\), può essere calcolato utilizzando la tabella 26.10-1 dell'ASCE 7-16. Questo parametro dipende dall'altezza dal livello del suolo del punto in cui viene considerata la pressione del vento, e la categoria di esposizione. Inoltre, i valori mostrati nella tabella si basano sulla seguente formula:
Per 15 piedi < \({z}\) < \({z}_{g}\): \({K}_{z} = 2.01(z/{z}_{g})^{2/α}\) (5)
Per \({z}\) < 15ft: \({K}_{z} = 2.01(15/{z}_{g})^{2/α}\) (6)
Dove:
tavolo 3. Valori di α e \({z}_{g}\) dal tavolo 26.11-1 dell'ASCE 7-16.
| Esposizione | un' | \({z}_{g}\) (ft) |
|---|---|---|
| B | 7 | 1200 |
| C | 9.5 | 900 |
| D | 11.5 | 700 |
Per questo esempio, prenderemo in considerazione l'elevazione dell'altezza di montaggio solare.
\({K}_{z} = 2.01((15)/(900))^{2/(9.5)} = 0.85 \)
\({K}_{z} = 0.85 \)
Pressione di velocità
Dall'equazione (3), possiamo risolvere per la pressione della velocità, \( {q}_{h}\) in psf, ad altezza di montaggio pari a 8.33 ft.
\({q}_{h} = 0.00256{K}_{z}{K}_{zt}{K}_{d}{K}_{e}V^2\)
\({q}_{h} = 0.00256(0.85)(1.0)(0.85)(0.987)(100)^2 = 18.256 psf\)
\({q}_{h} = 18.256 psf\)
Per calcolare la pressione del vento di progetto, useremo l'equazione (1). I dettagli di questi parametri sono mostrati di seguito.
Gust Effect Factor, \(G\)
Nella determinazione del fattore effetto raffica, \(G\), dobbiamo prima calcolare la frequenza naturale fondamentale della struttura \( {n}_{1} \). Se \( {n}_{1} \) è meno di 1 Hz, sarà classificato come struttura flessibile, quindi dovremo calcolare per \(G\) utilizzando la Sezione 26.11.5. In questo esempio, per un approccio semplificato, assumeremo che il nostro pannello solare sia rigido, dove \(G\) è uguale a 0.85 in base alla Sezione 26.11.1 dell'ASCE 7-16. Va notato che la due diligence nel controllare la frequenza naturale fondamentale della struttura è necessaria per determinare il fattore effetto raffica soprattutto per le strutture flessibili poiché amplificherà questo parametro.
Coefficiente di pressione netto, \({C}_{N}\), Angolo di inclinazione ≤ 45°
Per determinare i coefficienti di pressione netta, \( {C}_{N} \), assumeremo il pannello solare come edificio aperto con tetto a una falda. Possiamo ottenere questi valori dalla figura 27.3-4 dell'ASCE 7-16 con l'assunzione di “Flusso di vento chiaro.” Si noti che questi valori sono applicabili solo ai pannelli solari con angolo di inclinazione inferiore o uguale a 45°
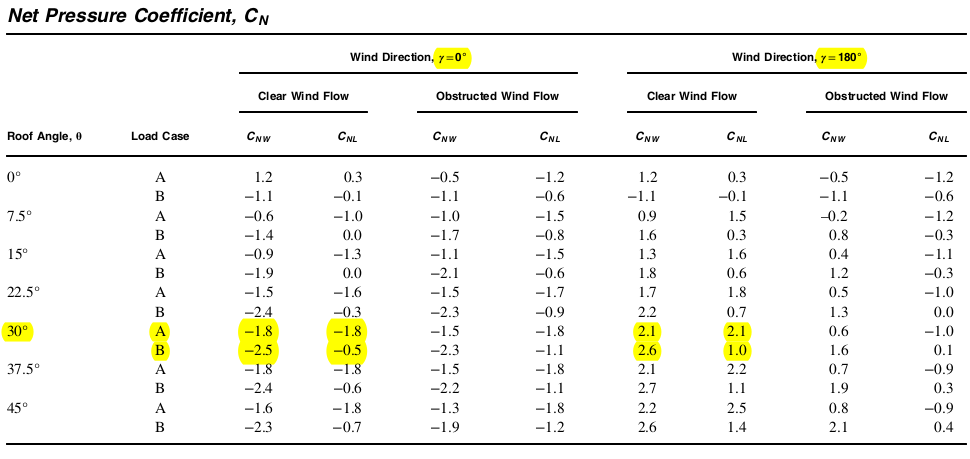
figura 6. Coefficiente di pressione netta, \( {C}_{N} \), valori dalla Figura 27.3-4 dell'ASCE 7-16 per edificio aperto con tetto a una falda.
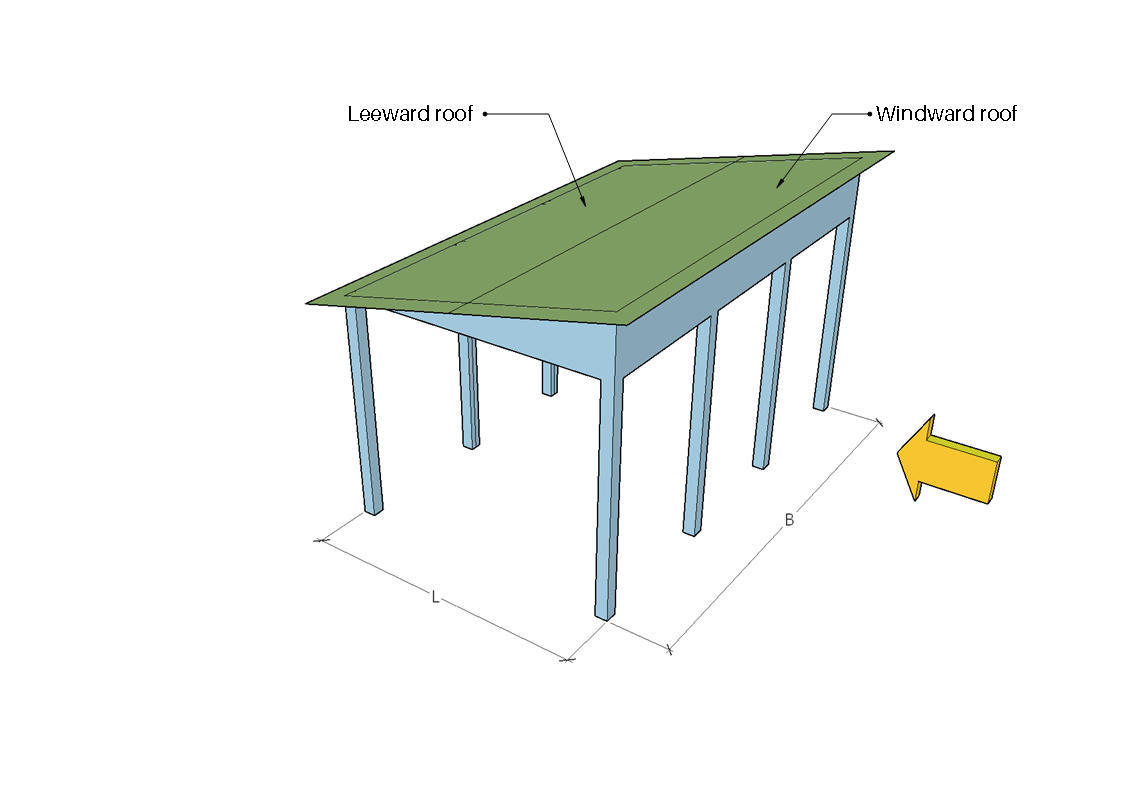
figura 7. Zone sopravvento e sottovento per angolo di direzione pari a 0° .
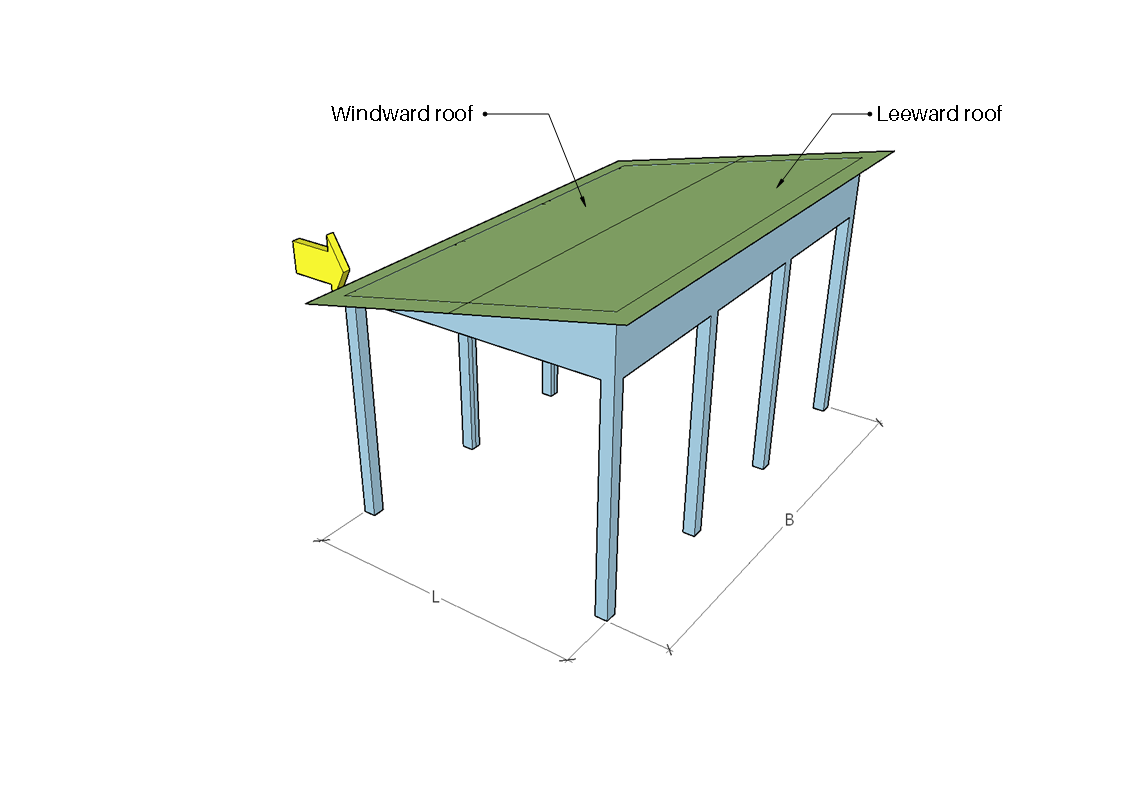
figura 8. Zone sopravvento e sottovento per angolo di direzione pari a 180°.
Poiché l'angolo di inclinazione del pannello solare è pari a 30°, i corrispondenti coefficienti di pressione netta, \( {C}_{N} \), da utilizzare sono i seguenti:
tavolo 4. Valori di \( {C}_{N} \) da utilizzare in base alla figura 27.3-4 dell'ASCE 7-16.
| Caso di carico | Direzione = 0° | Direzione = 180° | ||
|---|---|---|---|---|
| \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | \( {C}_{N,windward} \) | \( {C}_{N,leeward} \) | |
| A | -1.8 | -1.8 | 2.1 | 2.1 |
| B | -2.5 | -0.5 | 2.6 | 1.0 |
Si noti che un valore negativo indica che la pressione del vento agisce lontano dalla superficie e un valore positivo indica la pressione del vento che agisce verso la superficie. Dalla tabella 4, si può dedurre che ne considereremo quattro (4) casi di carico per il carico del vento sul nostro pannello solare.
Progettare le pressioni del vento – Angolo di inclinazione ≤ 45°
Nel calcolo del carico del vento sui pannelli solari con angolo di inclinazione > 45°, useremo l'equazione (1), quindi, i carichi del vento sui pannelli solari montati a terra:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
tavolo 5. I carichi del vento calcolati sui pannelli solari montati a terra da applicare alla struttura.
| Caso di carico | Direzione = 0° | Direzione = 180° | ||
|---|---|---|---|---|
| sopravvento, PSF |
Sottovento, PSF | sopravvento, PSF | Sottovento, PSF | |
| A | -27.932 | -27.932 | 32.587 | 32.587 |
| B | -38.794 | -7.759 | 40.346 | 15.518 |
Pertanto, i carichi del vento sui pannelli solari montati a terra quando applicati sono i seguenti:
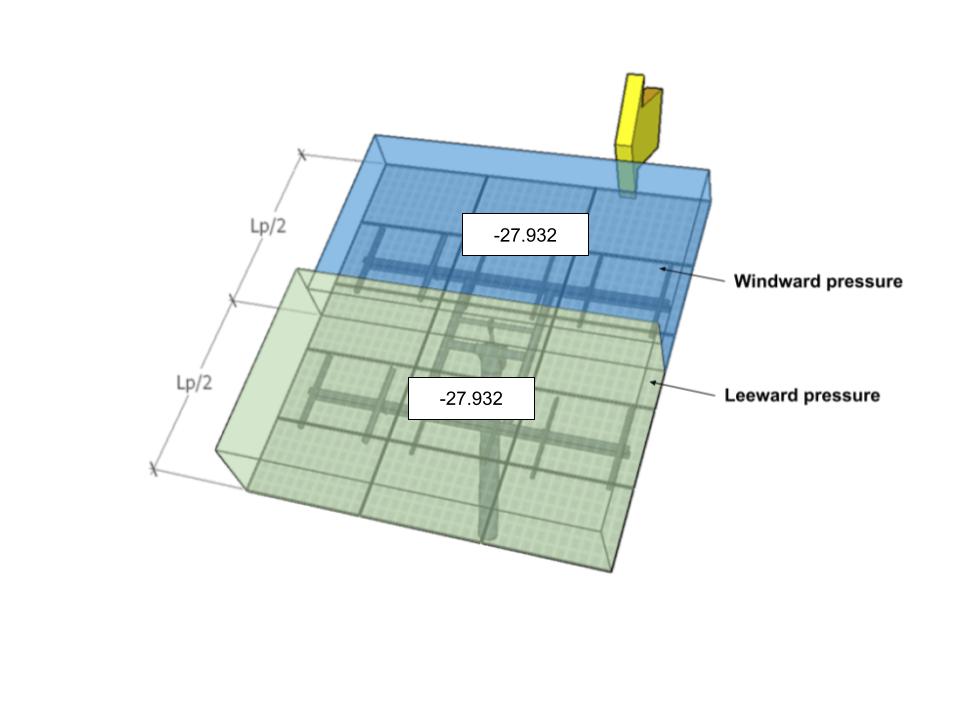
figura 9. Progettare le pressioni del vento per l'angolo di direzione 0° – Caso di carico A.
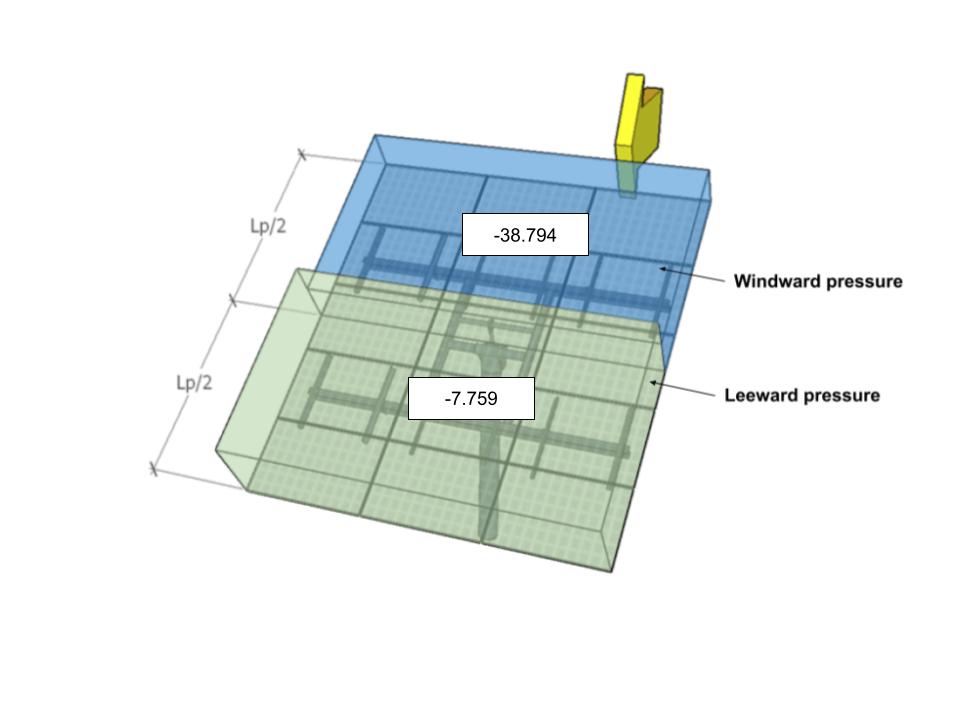
figura 10. Progettare le pressioni del vento per l'angolo di direzione 0° – Caso di carico B.
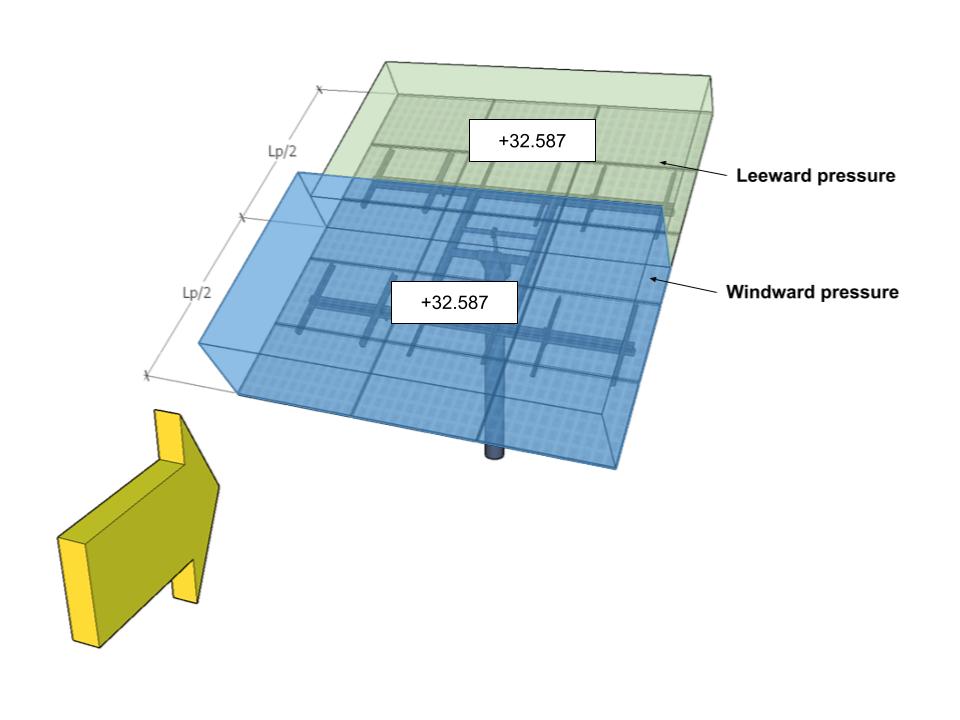
figura 11. Progettare le pressioni del vento per l'angolo di direzione 180° – Caso di carico A.
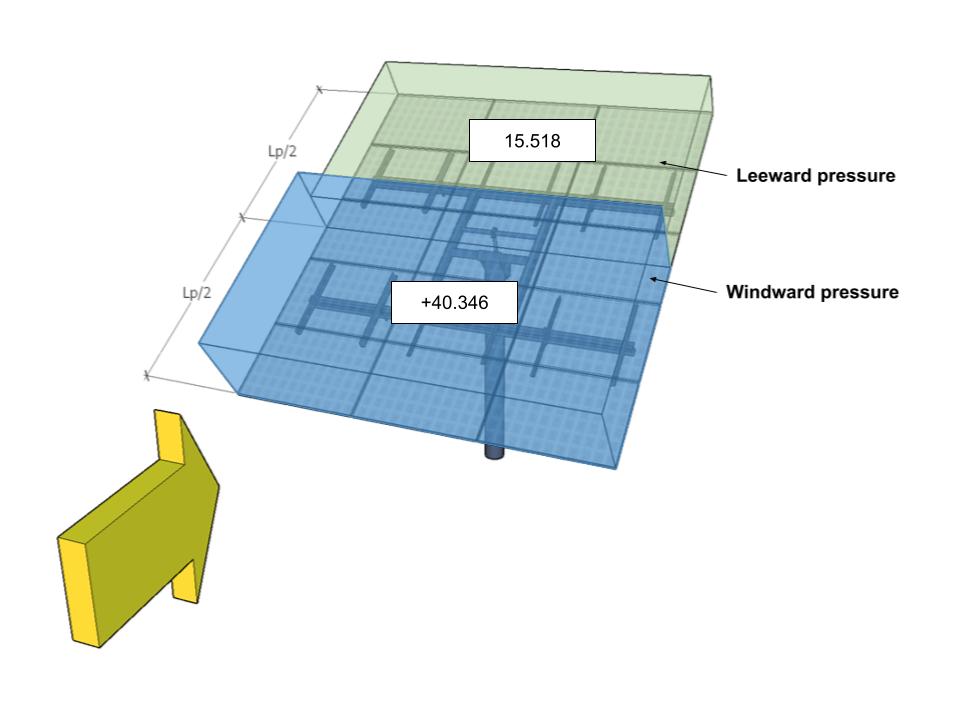
figura 12. Progettare le pressioni del vento per l'angolo di direzione 180° – Caso di carico B.
Coefficiente di forza netto, \({C}_{f}\), – Larghezza pannello > 45°
Diciamo che il nostro angolo di inclinazione del pannello solare è stato modificato in 60°. Dobbiamo usare la proiezione verticale del pannello solare e considerarla come un segno solido con la pressione di velocità calcolata fino alla sommità di questa proiezione.
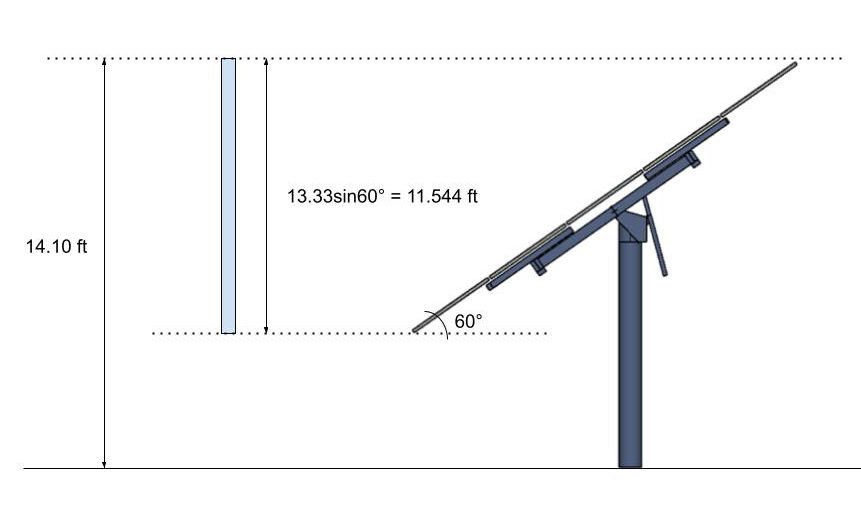
figura 13. La proiezione verticale del pannello solare è da considerarsi come segno solido.
Poiché l'altezza da terra alla sommità del progetto è ancora inferiore a 15 ft, possiamo ancora usare il nostro calcolato \( {K}_{z}\) sopra. Quindi, il valore calcolato di \( {q}_{h}\) sarebbe sempre lo stesso. La rete per il coefficiente, \( {C}_{f}\), da utilizzare è ricavabile dalla figura 29.3-1 dell'ASCE 7-16. Inoltre, nel calcolo di questi coefficienti di forza, considereremo solo il caso A per un approccio semplificato. Dalla figura 29.3-1:
\({q}_{h} = 18.256 psf\)
\( B = 16.25 ft\)
\( s = 11.544 ft\)
\( h = 14.102 ft\)
\( s/h = 0.818\)
\( B/s = 1.408\)
Dai valori tabulati di \( {C}_{f} \) in figura 29.3-1, interpoleremo i valori noti di \( B/s \) uguale a 1 e 2, e \( s/h \) uguale a 0.9 e 0.7.
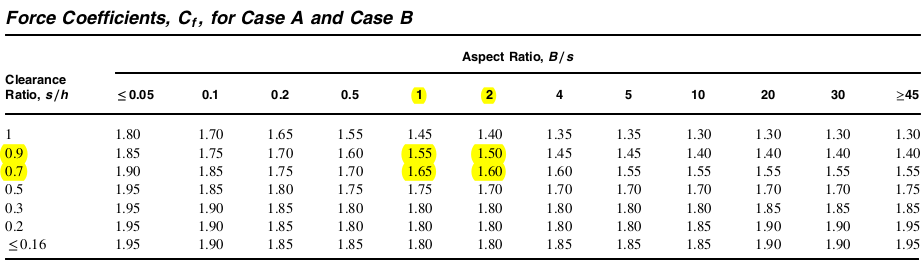
figura 14. Coefficiente di forza netto, \( {C}_{f} \), valori dalla Figura 29.3-1 dell'ASCE 7-16 per segni solidi.
Interpolando i valori evidenziati per ottenere \( {C}_{f} \) dal nostro \( B/s \) e \( s/h \), si ottiene:
\( {C}_{f} = 1.5706 \)
Progettare le pressioni del vento – Larghezza pannello > 45°
Nel calcolo del carico del vento sui pannelli solari con angolo di inclinazione > 45°, useremo l'equazione (2), quindi, i carichi del vento sui pannelli solari montati a terra:
\({q}_{h} = 18.256 psf\)
\( G = 0.85\)
\( {C}_{f} = 1.5706 \)
\(p = {q}_{h}G{C}_{f} = (18.256)(0.85)(1.5706) = 24.372 psf\)
\(p = 24.372 psf\)
Pertanto, i carichi del vento sui pannelli solari montati a terra quando applicati: 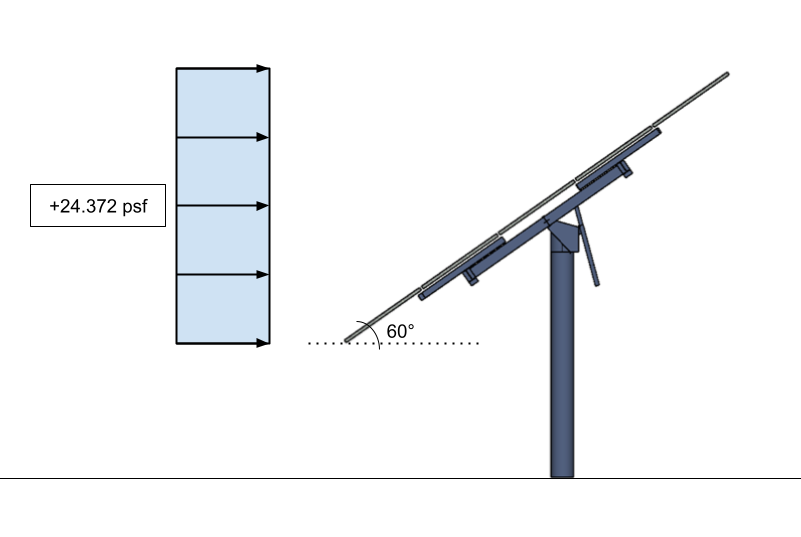
figura 15. La pressione del vento di progetto per il pannello solare come segno solido – applicato alla proiezione verticale.
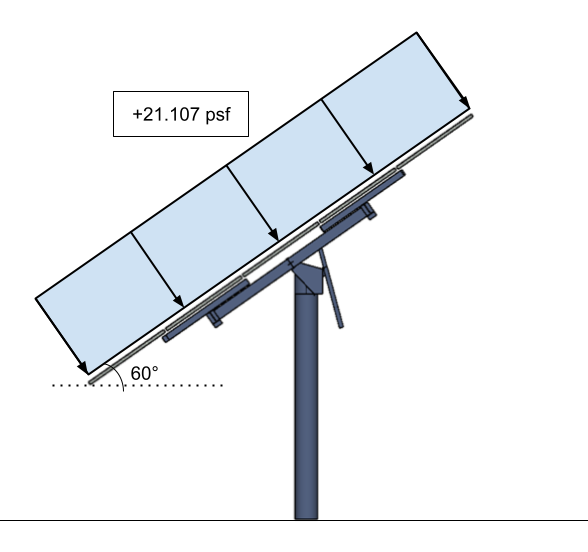
figura 16. La pressione del vento di progettazione convertita per il pannello solare come segno solido – applicato sulla superficie del pannello solare.
I calcoli del vento possono essere tutti eseguiti utilizzando SkyCiv Load Generator per ASCE 7-16 (calcolatore del carico del vento del pannello solare). Gli utenti possono inserire la posizione del sito per ottenere i dati sulla velocità del vento e sul terreno, inserire i parametri del pannello solare e generare le pressioni del vento di progetto. Con la versione standalone, puoi semplificare questo processo e ottenere un rapporto dettagliato sul calcolo del carico del vento per i pannelli solari!
Caricamento della neve
Per le zone innevate, dovrebbero essere considerati anche i carichi di neve sui pannelli solari. Per calcolare i carichi di neve per il nostro pannello solare, useremo il capitolo 7 dell'ASCE 7-16. Considereremo la struttura a pannelli solari come un edificio con tetto a una falda e considereremo solo il carico di neve bilanciato (carico di neve sul tetto inclinato). Le formule per determinare il carico di neve per il nostro pannello solare sono le seguenti:
Per calcolare il carico di neve sul tetto piano \({p}_{f} \):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \) (7)
Dove:
\({C}_{e} \) = fattore di esposizione
\({C}_{t} \) = fattore termico
\({I}_{s} \) = fattore di importanza per il carico di neve
\({p}_{g} \) = carico di neve al suolo, in psf
Per calcolare il carico di neve sul tetto inclinato \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \) (8)
Dove:
\({C}_{s} \) = fattore di pendenza del tetto
\({p}_{r} \) = sovrapprezzo pioggia su neve
Fattore di esposizione, \({C}_{e} \)
Il fattore di esposizione, \({C}_{e} \), può essere determinato dalla tabella 7.3-1 dell'ASCE 7-16 in base alla rugosità superficiale e all'esposizione del tetto. Dall'immagine satellitare della località che abbiamo ottenuto da Google Maps, possiamo classificare che la posizione è Rugosità superficiale C (terreno aperto con ostacoli sparsi che hanno altezze generalmente inferiori a 30 ft) e con il presupposto che i pannelli solari lo siano completamente esposto e senza ostacoli. Quindi, il Fattore di esposizione, \({C}_{e} \), della struttura è uguale a 0.9.
Fattore termico, \({C}_{t} \)
Il fattore termico, \({C}_{t} \), può essere determinato dalla tabella 7.3-2 dell'ASCE 7-16 in base alle condizioni termiche della struttura durante l'inverno. Dal tavolo, possiamo classificare il nostro pannello solare come “Strutture non riscaldate e all'aperto.” Pertanto, il corrispondente di Fattore termico, \({C}_{t} \), è per la struttura è uguale a 1.2.
Fattore di importanza per il carico di neve, \({I}_{s} \)
Il fattore di importanza per il carico di neve, \({I}_{s} \), può essere determinato dalla tabella 1.5-2 dell'ASCE 7-16 in base alla Categoria di Rischio della struttura. Poiché la struttura è classificata come Categoria di Rischio I, dal tavolo, \({I}_{s} \) è uguale a 0.8.
Carico di neve al suolo, \({p}_{g} \)
Il carico di neve al suolo, \({p}_{g} \), può essere determinato dalla figura 7.2-1 dell'ASCE 7-16 come mostrato di seguito. Da questa figura, il il carico di neve al suolo, \({p}_{g} \) per il nostro pannello solare è uguale a 10 PSF.
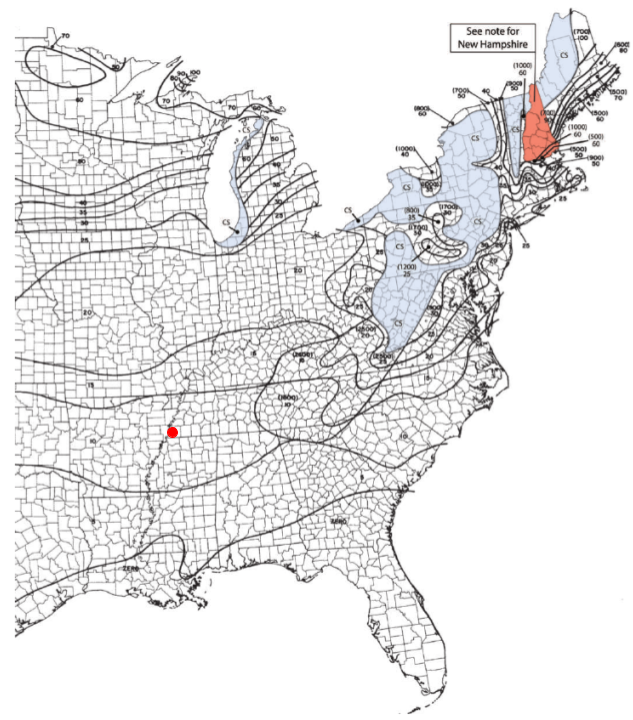
figura 17. Mappa del carico di neve al suolo dalla figura 7.2-1 dell'ASCE 7-16 con punto rosso per indicare la posizione del nostro pannello solare.
SkyCiv automatizza anche i calcoli del carico di neve al suolo con alcuni parametri. Prova il nostro Calcolatore del carico del vento del pannello solare
Carico di neve sul tetto piano, \({p}_{f} \)
Dai parametri sopra, possiamo già calcolare il carico di neve sul tetto piano, \({p}_{f} \), utilizzando l'equazione (7):
\({p}_{f} = 0.7{C}_{e}{C}_{t}{I}_{s}{p}_{g} \)
\({p}_{f} = 0.7(0.9)(1.2)(0.8)(10) = 6.048 psf \)
\({p}_{f} = 6.048 psf \)
Fattore di pendenza del tetto, \({C}_{s} \)
Il fattore di pendenza del tetto può essere calcolato dalla figura 7.4-1 dell'ASCE 7-16 a seconda dell'angolo di inclinazione, l'ostruzione al di sotto della superficie del tetto, e il valore del fattore termico \({C}_{t} \). Per il nostro pannello solare, assumeremo che il nostro pannello solare sia classificato come “Superficie scivolosa.” Dal fattore termico \({C}_{t} \) è uguale a 1.2, possiamo già interpolare il valore di \({C}_{s} \) da 7-2c. Dal grafico, i valori conosciuti sono:
\({C}_{s} = 1.0 \) for 15°
\({C}_{s} = 0.0 \) for 70°
Interpolando questi valori possiamo ottenere:
\({C}_{s} = 0.727 \) for 30°
Pertanto, \({C}_{s} = 0.727 \) per il nostro pannello solare.
Sovrapprezzo pioggia su neve, \({p}_{r} \)
Un ulteriore 5 psf sovrapprezzo pioggia su neve, \({p}_{r} \), dovrebbe essere preso in considerazione per le posizioni in cui \({p}_{g} \) è minore o uguale a 20 psf ma non zero, per tutti i tetti con inclinazione (in gradi) meno di \( W/50 \) gradi dove \( W \) è la distanza orizzontale dalla gronda al colmo. Il valore di \({p}_{r} \) si applica solo al tetto spiovente (equilibrato) caso di carico. Per questo esempio:
\(W = 13.33 cos 30° = 11.544 ft \)
\( W/50 =0.231° \)
Da \({p}_{g} = 10 psf \) ma l'angolo di inclinazione di 30° è maggiore di \( W/50 =0.231° \), \({p}_{r} \) può essere trascurato ed è uguale a 0.0
Carico di neve sul tetto inclinato, \({p}_{s} \)
Dall'equazione (8), possiamo calcolare il carico di neve del tetto inclinato \({p}_{s} \):
\({p}_{s} = {C}_{s}{p}_{f} + {p}_{r} \)
\({p}_{s} = (0.727)(6.048) + 0.0 = 4.397 psf \)
\({p}_{s} = 4.397 psf \)
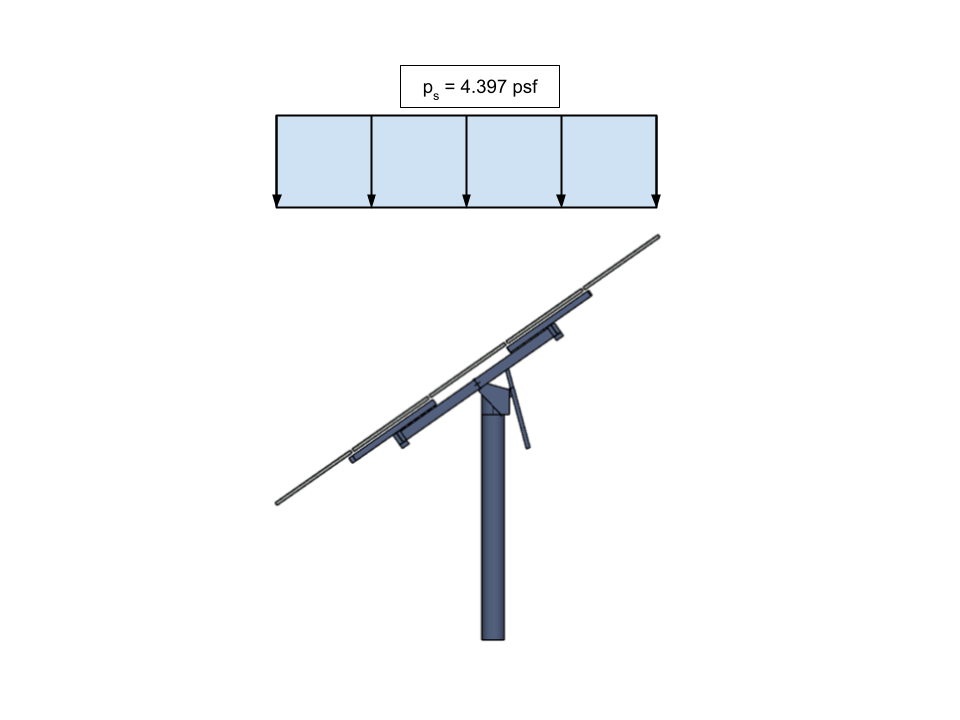
figura 18. Il carico di neve bilanciato calcolato (carico di neve sul tetto inclinato) per il pannello solare applicato sulla sporgenza orizzontale della struttura.
Nota che \({p}_{s} \) si applica sulla proiezione orizzontale della struttura. Dovremo convertire questo valore in un carico di pressione inclinato equivalente in modo da poterlo applicare al nostro modello.
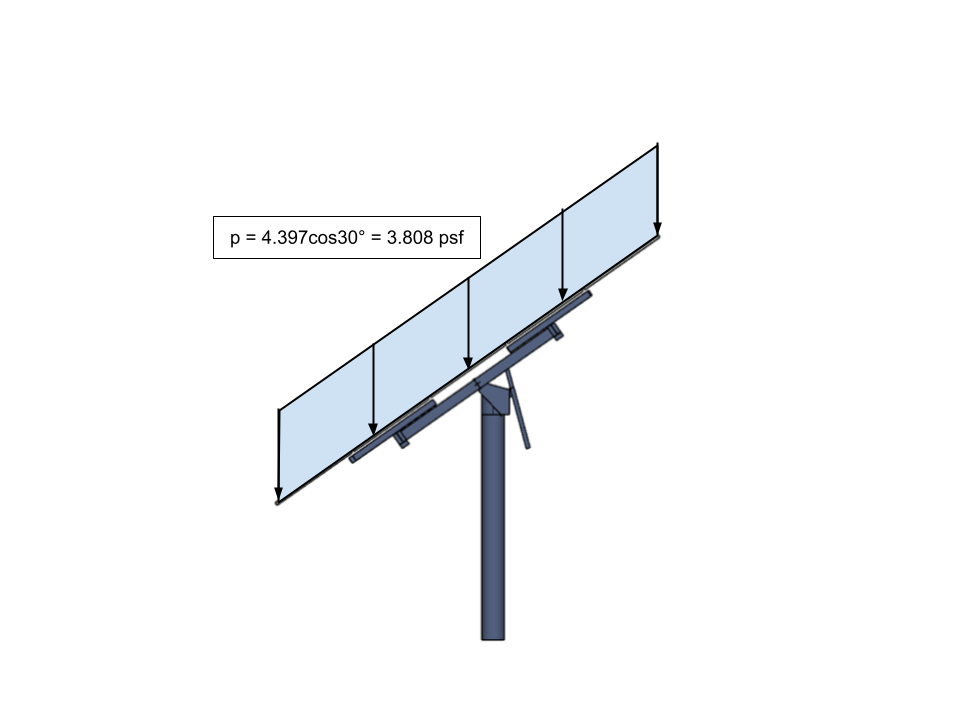
figura 19. Il carico di neve bilanciato convertito (carico di neve sul tetto inclinato) per il pannello solare da applicare al nostro modello.
I calcoli del carico di neve possono essere eseguiti anche in SkyCiv Load Generator per ASCE 7-16. Tuttavia, è disponibile solo nella nostra versione standalone e nell'account professionale.
Generatore di carico SkyCiv
adottato a causa della posizione della struttura, puoi ottenere carichi di vento e carichi di neve su pannelli solari montati a terra con pochi clic e input. Quando acquisti la versione standalone o ti registri per un account Professional, sarai in grado di generare il rapporto dettagliato sui calcoli di vento e neve per il tuo progetto di pannelli solari!
Puoi controllare il rapporto dettagliato sul carico di vento e neve per il pannello solare attraverso questi link:
inoltre, puoi anche creare il tuo calcolatore del carico del vento del pannello solare utilizzando l'API SkyCiv Load Generator, proprio come abbiamo creato una soluzione per uno dei nostri clienti. Con pochi input, progetterà automaticamente il sistema di pannelli solari per te. Puoi controllare la nostra documentazione API attraverso questo collegamento.
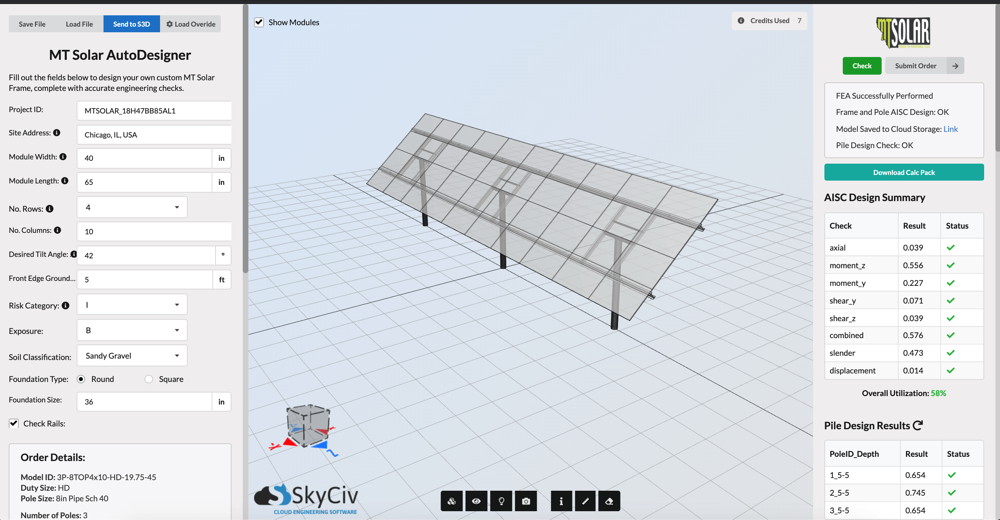
figura 20. La nostra soluzione personalizzata per pannelli solari creata per MT Solar utilizzando l'API SkyCiv.
Per risorse aggiuntive, puoi usare questi link:
- Introduzione a SkyCiv Load Generator
- ASCE 7-16 Calcoli del carico del vento (Pannelli solari)
- ASCE 7 Calcoli del carico di neve
- Come calcolare e applicare i carichi alla deriva della neve sul tetto con ASCE 7-10
- Calcolo dei carichi di neve sul tetto con ASCE 7-10
Ingegnere strutturale, Sviluppo del prodotto
MS Ingegneria Civile
Riferimenti:
- Coulbourne, W. L., & Stafford, T. E. (2020, aprile). Carichi del vento: Guida alle disposizioni sul carico del vento di ASCE 7-16. American Society of Civil Engineers.
- American Society of Civil Engineers. (2017, giugno). Carichi minimi di progetto e criteri associati per edifici e altre strutture. American Society of Civil Engineers.
- Posizione della struttura e direzione della sorgente del vento corrispondente
- MT Solar


