Nel design della connessione in acciaio, bulloni sono generalmente progettati come un gruppo di bulloni che fungerà da corpo unico per resistere a un determinato carico. La forza di un gruppo di bulloni è solitamente calcolata dalla forza di controllo del suo bullone più critico. I carichi diretti sono distribuiti sul numero totale di bulloni, mentre il momento indotto dovuto all'eccentricità dei carichi è distribuito in relazione al momento di inerzia del gruppo di bulloni e alla distanza dal baricentro. Questa analisi è chiamata analisi elastica. A causa delle sue ipotesi semplificate e conservative sulla distribuzione del carico, spesso produce connessioni bullonate sovradimensionate.
Quando si parla di ingegneria del valore e design economici, l'approccio anelastico è preferito dalla maggior parte dei produttori. Richiede un numero minore di bulloni per la stessa entità dei carichi. Per fare l'approccio anelastico, il centro istantaneo di rotazione (ICOR) il metodo che utilizza le iterazioni è il modo migliore.
In questo articolo, dimostreremo come calcolare la forza di a connessione bullonata utilizzando il metodo ICOR. Le reazioni per bullone verranno calcolate utilizzando l'equazione (7-1) sulle pagine 7-7 del Manuale AISC 15a edizione. Questo verrà quindi utilizzato per verificare se la posizione presunta del centro istantaneo del gruppo di bulloni è corretta. Infine, una volta che abbiamo la posizione corretta dell'IC, calcoleremo quindi il coefficiente del gruppo di bulloni C per determinarne la forza.
L'uso del metodo ICOR per ottenere il coefficiente del gruppo di bulloni è un processo lungo in quanto richiede un metodo per tentativi ed errori per ottenere il centro istantaneo (CIRCUITO INTEGRATO) Posizione. Al giorno d'oggi, con l'uso di risolutori informatici, l'IC di un gruppo di bulloni può essere facilmente calcolato utilizzando iterazioni programmate. Risolutore di gruppi Bolt SkyCiv utilizza un metodo di iterazione veloce per determinare la posizione del circuito integrato e il coefficiente del gruppo di bulloni in pochi secondi. Attualmente è implementato nell'AS 4100 codice di progettazione, ma sarà presto integrato nel resto dei codici di progettazione.
Ottenere le proprietà del gruppo di bulloni
Iniziamo la nostra semplice analisi su un gruppo di quattro bulloni caricato con un carico di taglio verticale eccentrico di 10 kips. L'eccentricità del carico lungo l'asse x è 4 pollici a destra del gruppo di bulloni. L'angolo dalla verticale è zero e l'eccentricità lungo l'asse y è zero.
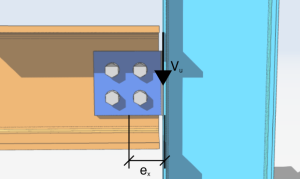
\(V_{u} = 10 chicchi \)
\(\teta = 0 gradi)
\(e_{x} = 4 in)
\(e_{y} = 0 pollici)
La prima cosa da fare è ottenere le coordinate di tutti i bulloni nel nostro gruppo di bulloni. L'uso di guide e tabelle visive è altamente raccomandato.
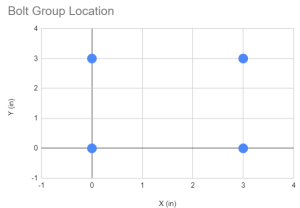
| ID negozio | X (pollici) | E (pollici) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
Per ottenere il baricentro del gruppo di bulloni lungo la x- e gli assi y, abbiamo bisogno della formula seguente.
Permettere \(n \) = numero totale di bulloni
\(X_{CG} = frac{\somma X}{n}\)
\(Il modulo con calcola la dimensione dell'asta di ancoraggio{CG} = frac{\somma Y}{n} \)
Poi, la nostra soluzione è:
\(X_{CG} = frac{\somma X}{n} = frac{0 pollici + 0 pollici + 3 pollici + 3 pollici}{4} = 1.5 in)
\(Il modulo con calcola la dimensione dell'asta di ancoraggio{CG} = frac{\somma Y}{n} = frac{0 pollici + 3 pollici + 0 pollici + 3 pollici}{4} = 1.5 in)
Assumi la posizione dell'I.C.
Dopo aver ottenuto il baricentro, assumeremo la posizione del centro istantaneo \(CIRCUITO INTEGRATO). Come primo tentativo, possiamo supporre che l'IC si trovi al baricentro geometrico del gruppo di bulloni.
Quindi, assumere
\(X_{CIRCUITO INTEGRATO} = X_{CG} = 1.5 in)
\(Il modulo con calcola la dimensione dell'asta di ancoraggio{CIRCUITO INTEGRATO} = S_{CG} = 1.5 in)
Poi, tabulare lo spostamento di ciascun bullone nella posizione dell'IC. Possiamo farlo semplicemente ottenendo prima la distanza lungo x e la distanza lungo y, quindi ottenere il suo spostamento
| ID negozio | cx (pollici) | ci (pollici) | c (pollici) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
Dove,
\(c_{x} = X_{io} – X_{CIRCUITO INTEGRATO}\)
\(c_{y} = S_{io} – Il modulo con calcola la dimensione dell'asta di ancoraggio{CIRCUITO INTEGRATO}\)
\(c = sqrt{{\sinistra(c_{x} \giusto)}^{2} + {\sinistra(c_{y} \giusto)}^{2}}\)
Per il bullone n. 1, la nostra soluzione è
\(c_{x} = 0 pollici – 1.5 in = -1.5 in)
\(c_{y} = 0 pollici – 1.5 in = -1.5 in)
\(c = sqrt{{\sinistra( -1.5 in destra)}^{2} + {\sinistra( -1.5 in destra)}^{2}} = 2,121 pollici)
Calcolare la deformazione per bullone rispetto alla distanza da IC
conseguentemente, dopo aver ottenuto le distanze dei bulloni dalla posizione IC presunta, calcoliamo quindi la deformazione di ciascun bullone in funzione della sua distanza.
La deformazione massima per bullone, impostato \(\Delta_{max} = 0.34 in), si basa su dati sperimentali per un bullone ASTM come descritto nella pagina AISC 7-8. Usando la proporzione lineare, e impostazione \(\Delta_{max} = 0.34 in), possiamo calcolare la deformazione di un singolo bullone rispetto alla sua porzione alla distanza massima \(c_{max}\). L'equazione per ottenere è mostrato di seguito.
\(\Delta_{1} = 0,34 pollici volte sinistra( \frac{c}{c_{max}}\giusto) \)
Per il bullone n. 1, la deformazione è
\(\Delta_{1} = 0,34 pollici volte sinistra( \frac{2.121 pollici}{2.121 pollici}\giusto)\)
Per il resto dei bulloni, le deformazioni calcolate sono elencate di seguito.
| ID negozio | \(\Delta\) (pollici) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Ottieni le reazioni per bullone
Una volta che abbiamo la deformazione per bullone, possiamo quindi utilizzare AISC 15th Ed. Eq (7-1) per ottenere le reazioni per bullone.
\(R = R_{ult} \sinistra ( 1 – e^{-10\Delta}\giusto )^{0.55}\)
La \(R_{ult}\) nell'equazione è il carico ultimo presunto su un bullone, che possiamo impostare come resistenza al taglio del bullone.
\(R_{ult} = phi R_{n} \)
Per il nostro esempio, useremo una resistenza al taglio del bullone di \(24.4 ciao). È anche consentito utilizzare un altro valore poiché questo si annullerà semplicemente quando calcoliamo il coefficiente del gruppo di bulloni \(C) più tardi.
Per il bullone n. 1, la reazione calcolata è
\(R = R_{ult} \sinistra ( 1 – e^{-10\Delta}\giusto )^{0.55}\)
\(R = 24.4 kip sinistra ( 1 – e^{-10 \volte sinistra ( 0.34 in destra )}\giusto )^{0.55}\)
\(R = 23.949 ciao)
Per il resto dei bulloni, le reazioni calcolate sono le seguenti. Allo stesso tempo, le componenti della reazione del bullone \(R) lungo x e y sono mostrati anche.
| ID negozio | R (kip) | Trova la distribuzione delle sollecitazioni in una piastra quadrata a causa degli effetti di un foro circolare al centro sotto un carico lineare uniforme nel piano (kip) | Ry (kip) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
Per il bullone n. 1, le soluzioni per ottenere le componenti x e y sono mostrate di seguito.
\(R_{x} = -R sinistra ( \frac{c_{y}}{c} \giusto ) = -23.949 \volte sinistra ( \frac{-1.5pollici}{2.121pollici} \giusto ) = 23.949 ciao)
\(R_{y} = R sinistra ( \frac{c_{x}}{c} \giusto ) = 23.949 \volte sinistra ( \frac{1.5pollici}{2.121pollici} \giusto ) = 23.949 ciao)
Inoltre, dovremmo ottenere il momento di carico indotto per bullone a causa dell'eccentricità. Per calcolare questo, usiamo i componenti \(R_{x}\) e \(R_{y}\) e moltiplicali per le eccentricità \(c_{y}\) e \(c_{x}\), rispettivamente.
Per il bullone n. 1, la seconda reazione all'IC è
\(M_{r} = -R_{x}c_{y} + -R_{y}c_{x} \)
\(M_{r} = -16.937 kip times sinistra ( -1.5in destra) + -16.937 kip times sinistra ( -1.5 in destra ) \)
\(M_{r} = 50.811 pollo dentro)
Per il resto dei bulloni, le reazioni dei momenti corrispondenti sono elencate di seguito.
| ID negozio | Sig (pollo-in) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀Signor = 101.622 |
Verifica della posizione dell'IC
Ora che abbiamo le reazioni di taglio e momento per bullone, lo useremo per determinare la quantità di carico Pu a cui questo gruppo di bulloni resiste. Per fare questo, otterremo la risultante della somma di tutte le reazioni lungo x e la somma di tutte le reazioni lungo y.
Dalla sezione precedente, l'abbiamo calcolato
\(\somma R_{x}=0kip\)
e
\(\somma R_{y}=0kip\)
Quindi,
\(Design di piastre di base in acciaio con piccolo momento{u} = sqrt{{\sinistra( \somma R_{x} \giusto)}^{2} + {\sinistra( \somma R_{y} \giusto)}^{2}} = 0 ciao)
Dal momento che il carico risultante \(Design di piastre di base in acciaio con piccolo momento{u} = 0kip), possiamo decidere a questo punto di non procedere con la verifica poiché i nostri dati saranno proprio zero. Possiamo anche dedurre che la prima posizione ipotizzata di I.C., che è al baricentro del gruppo di bulloni, non è corretto. Tuttavia, ai fini di questa discussione, procederemo con i passaggi seguenti.
\(Design di piastre di base in acciaio con piccolo momento{ux} = -P_{u}peccatosinistra ( \theta right ) = 0 kip \)
\(Design di piastre di base in acciaio con piccolo momento{uy} = -P_{u}cossinistra ( \theta right ) = 0 kip \)
\(M_{u} = -P_{ux}\sinistra ( Il modulo con calcola la dimensione dell'asta di ancoraggio{CG} + e_{y} – Il modulo con calcola la dimensione dell'asta di ancoraggio{CIRCUITO INTEGRATO} \giusto ) + -Design di piastre di base in acciaio con piccolo momento{uy} \sinistra (X_{CG} + e_{x} – X_{CIRCUITO INTEGRATO} \giusto ) = 0 kip \)
Da,
\(Design di piastre di base in acciaio con piccolo momento{ux} \neq somma R_{x} \)
\(Design di piastre di base in acciaio con piccolo momento{uy} \neq somma R_{y} \)
\(M_{u} \non sono M_{r} \)
Pertanto, la presunta sede di I.C. non è corretto. Possiamo ora procedere con la prossima posizione ipotizzata.
SkyCiv ha la piena integrazione del calcolo del gruppo di bulloni nel modulo standard australiano. Vuoi provare il nostro software di progettazione delle connessioni?
Seconda Iterazione
Per la nostra seconda iterazione, assumiamo che l'I.C. si trova alle coordinate indicate di seguito.
Assumere
\(X_{CIRCUITO INTEGRATO} = 0.062 in)
\(Il modulo con calcola la dimensione dell'asta di ancoraggio{CIRCUITO INTEGRATO} = 1.5 in)
Poi, facciamo i passaggi che abbiamo fatto nella nostra prima iterazione. In sintesi, la tabella sottostante mostrerà le coordinate, la distanza di ciascun bullone dal presunto I.C, e la corrispondente deformazione rispetto alla distanza.
| ID negozio | X (pollici) | E (pollici) | cx (pollici) | ci (pollici) | c (pollici) | \(\Delta\) (pollici) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Si noti che il baricentro calcolato del gruppo di bulloni è sempre lo stesso poiché non è cambiato nulla sulle coordinate dei bulloni.
\(X_{CG} = 1.5 in)
\(Il modulo con calcola la dimensione dell'asta di ancoraggio{CG} = 1.5 in)
Poi, calcoliamo le reazioni lungo x, reazioni lungo y, e il momento corrispondente. I valori sono tabulati di seguito.
| ID negozio | R (kip) | Trova la distribuzione delle sollecitazioni in una piastra quadrata a causa degli effetti di un foro circolare al centro sotto un carico lineare uniforme nel piano (kip) | Ry (kip) | Sig (pollo-in) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀Signor = 222 |
Successivamente, determiniamo il carico risultante di tutte le reazioni lungo x e y.
\(Design di piastre di base in acciaio con piccolo momento{u} = sqrt{{\sinistra( \somma R_{x} \giusto)}^{2} + {\sinistra( \somma R_{y} \giusto)}^{2}}\)
\(Design di piastre di base in acciaio con piccolo momento{u} = sqrt{{\sinistra( 0 kipdestra)}^{2} + {\sinistra( 40.703 kipdestra)}^{2}}\)
\(Design di piastre di base in acciaio con piccolo momento{u} = 40.703 ciao)
Poi, le componenti del carico risultante in base al dato \(\theta) è mostrato di seguito.
\(Design di piastre di base in acciaio con piccolo momento{ux} = -P_{u}peccato sinistra ( \theta right ) = -41kip times sin sinistra ( 0 gradi destra )= 0 ciao)
\(Design di piastre di base in acciaio con piccolo momento{uy} = -P_{u}cos sinistra ( \theta right ) = -41kip volte cos sinistra ( 0 gradi destra )= -41 ciao)
Utilizzeremo quindi questi componenti per risolvere per il momento il carico sul presunto I.C.
\(M_{u} = -P_{ux} \sinistra ( Il modulo con calcola la dimensione dell'asta di ancoraggio{CG} + e_{y} – Il modulo con calcola la dimensione dell'asta di ancoraggio{CIRCUITO INTEGRATO} \giusto) + Design di piastre di base in acciaio con piccolo momento{uy} \sinistra ( X_{CG} + e_{x} – X_{CIRCUITO INTEGRATO} \giusto)\)
\(M_{u} = -0 kip sinistra ( 1.5 pollici +0 pollici – 1.5 in destra) + 41 kip sinistra ( 1.5 pollici +4 pollici – 0.06 in destra)\)
\(M_{u} = -222 pollo dentro)
Successivamente, confrontiamo il calcolato Pux, Pux, e Mu alle reazioni del gruppo dei bulloni.
\(Design di piastre di base in acciaio con piccolo momento{ux} \ca – \somma R_{x}\)
\(Design di piastre di base in acciaio con piccolo momento{uy} \ca – \somma R_{y}\)
\(M_{u} \ca – \somma M_{u}\)
Poiché il lato sinistro è quasi uguale al lato destro dell'equazione, possiamo dire che la presunta ubicazione di I.C. è corretta!
Risolvere il coefficiente C
Una volta che l'I.C. la posizione è determinata, ora possiamo ottenere il coefficiente del gruppo di bulloni C con la formula seguente.
\(C = frac{Design di piastre di base in acciaio con piccolo momento{u}}{\Phi R_{n}} = \frac{40.703 kip}{24.4 kip} = 1.668\)
Calcolatore di gruppi di bulloni gratuito
Controlla come progettiamo le nostre connessioni bullonate con questo approccio usando il nostro Calcolatrice gratuita per la progettazione di connessioni in acciaio! Per più funzionalità, iscriviti oggi stesso al nostro software Structural 3D per iniziare!

