Il baricentro o centro di massa delle sezioni della trave è utile per l'analisi della trave quando il momento di inerzia è richiesto per calcoli come taglio/sollecitazione di flessione e la deflessione . Questo articolo ti guida attraverso un semplice processo su come calcolare il centroide e ti presenta SkyCiv Free Centroid Calculator.
Come trovare il centroide
Prima di tutto, devi sapere come trovare il centroide. Le sezioni della trave sono generalmente costituite da una o più forme. Quindi, per trovare il baricentro di un'intera area della sezione del raggio, prima deve essere suddiviso in segmenti appropriati. Dopodichè, l'area e il baricentro di ogni singolo segmento devono essere considerati per trovare il baricentro dell'intera sezione.
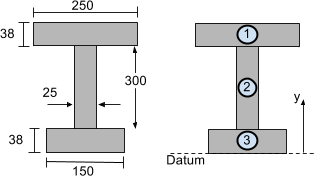
Considera la sezione I-beam mostrata di seguito. Per calcolare il centroide verticale (nella direzione y) può essere suddiviso in 3 segmenti come illustrato:
Ora dobbiamo semplicemente usare l'equazione del baricentro per trovare la verticale (y) di una forma a più segmenti:

Prenderemo il datum o la linea di riferimento dalla parte inferiore della sezione della trave. Ora troviamo Aio e yio per ogni segmento della sezione della trave a I mostrata sopra in modo da poter trovare il centroide verticale o y.
[matematica]
\testo{Segmento 1:}\\
\inizio{allineare}
{A}_{1} &= 250 times38 = 9500 {\testo{ mm}}^{2}\\
{y}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \testo{ mm}\\\\
\fine{allineare}
[matematica]
[matematica]
\testo{Segmento 2:}\\
\inizio{allineare}
{A}_{2} &= 300 times25 = 7500 {\testo{ mm}}^{2}\\
{y}_{2} &= 38 + \tfrac{300}{2} = 188 \testo{ mm}\\\\
\fine{allineare}
[matematica]
[matematica]
\testo{Segmento 3:}\\
\inizio{allineare}
{A}_{3} &= 38 times150 = 5700 {\testo{ mm}}^{2}\\
{y}_{3} &= tfrac{38}{2} = 19 testo{ mm}\\\\
\fine{allineare}
[matematica]

Nel caso in cui la sezione trasversale sia composta da due materiali o da un materiale composito, quindi uno dei materiali dovrà essere moltiplicato per il rapporto modulare in modo tale che l'intera sezione dell'equazione diventi uniforme.
[matematica]
n = frac{E_{1}}{E_{2}}
[matematica]
Generalmente, E1 è il modulo di elasticità del materiale non prevalente, e E2 è il modulo di elasticità del materiale prevalente, sebbene qualunque ordine sia preferito non influenzerà la soluzione del centroide. Regolazione per il secondo materiale, l'equazione del baricentro diventa la seguente.
[matematica]
\bar{y}= Frac{\somma{A}_{io}{y}_{io}+\somma {n}{A}_{io}{y}_{io}}{\somma{A}_{io}+\somma {n}{A}_{io}}
[matematica]
Trova il baricentro del raggio con SkyCiv
Trovare il baricentro del raggio è importante, ma calcolarli manualmente può richiedere molto tempo. SkyCiv offre a Calcolatore del centroide gratuito che automatizza questo processo per te, aiutandoti a trovare la verticale (y) e orizzontale (x) centroidi delle sezioni della trave in modo semplice e preciso!
Questo strumento è una versione gratuita di Il Generatore di Sezioni SkyCiv, un software completo di analisi delle sezioni online per analizzare la geometria, curvatura, proprietà della sezione a taglio e torsione, nonché FEA e progettazione in cemento armato. Con questo strumento, puoi creare sezioni personalizzate utilizzando modelli predefiniti o definire le tue forme con punti, Linee, o importazioni DXF da CAD.
Per esplorare tutte le funzionalità Il Generatore di Sezioni SkyCiv e sperimenta la facilità di modellare e analizzare la tua sezione, Iscriviti gratuitamente oggi!
Risorse correlate


