In questo articolo, svilupperemo un esempio di progettazione del solaio utilizzando l'ultima versione di ACI-318-19: “Requisiti del codice di costruzione per calcestruzzo strutturale,” costituito dalla modellazione in SkyCiv di un edificio basso in cemento armato incentrato sul confronto dei risultati del software e dei calcoli manuali secondo un metodo accettato da ACI: “Il metodo di progettazione diretta per le lastre.” Questa procedura consiste nell'assegnare in diverse strisce lungo le direzioni principali e i telai dell'edificio il momento totale mediante fattori convenienti per determinare la quantità di armatura e la posizione nella soletta.
Ci auguriamo che tu abbia letto l'articolo precedente, Progettazione di lastre in S3D, per presentarti alla modellazione e alla progettazione di lastre utilizzando SkyCiv. Un'altra informazione utile che ti suggeriamo di considerare si trova in Come modellare i piatti? Una volta completata la lettura di entrambi i documenti, sentiti libero di immergerti nel seguente esempio di confronto di lastre completamente lavorate!
Disposizione generale dell'edificio
Le immagini seguenti mostrano una vista isometrica e le dimensioni in pianta dell'esempio da calcolare. L'edificio ha due lastre piane sopraelevate senza travi tra i pilastri.
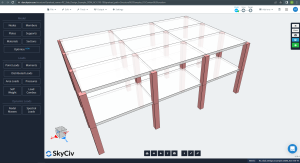
figura 1. Vista isometrica dell'esempio di edificio
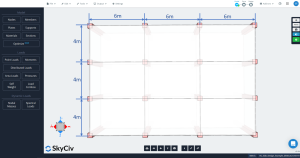
figura 2. Dimensioni in pianta della lastra
Metodo di progettazione diretta per lastre bidirezionali (DDM)
Limitazioni
ACI 318 consente di utilizzare il DDM per progettare solette in cemento armato per carichi gravitazionali, che raccolgono alcuni requisiti secondo la geometria, relazioni di carico, simmetria, eccetera. Possiamo riassumere queste limitazioni nel seguente elenco (Note PCA):
- “Ci devono essere tre o più campate continue in ciascuna direzione.”: figura 2 mostra tre campate in ciascuna direzione principale, longitudinale e trasversale. Ok!
- “I pannelli della soletta devono essere rettangolari con un rapporto di campata maggiore o minore (dalla linea centrale alla linea centrale dei supporti) non maggiore di 2.”: Secondo figura 2, il rapporto è pari a \({\frac{l_1}{4}= Frac{6m}{4m}=1,5 < 2}\). Ok!
- “Lunghezze di campate successive (dalla linea centrale alla linea centrale dei supporti) in ciascuna direzione non deve differire di più di 1/3 della campata più lunga”. Le lunghezze della campata sono le stesse in ogni direzione, 6m longitudinale e 4 m trasversale. Ok!
- “Le colonne non devono essere sfalsate più di 10% della campata (nella direzione dell'offset) da entrambi gli assi tra le linee centrali delle colonne successive”. L'esempio di edificio non ha offset nelle colonne. Ok!
- “I carichi devono essere distribuiti uniformemente, con il carico in tempo reale senza fattore o servizio non più di due volte il carico inattivo senza fattore o servizio (L/D ≤ 2)”. Prendendo i valori di ciascun carico gravitazionale, il rapporto è definito come \({\frac{L}{D}= Frac{2}{7.8}=0,256 < 2}\). Ok!.
- “Per solai portanti travetti a due vie, la rigidità relativa delle travi in due direzioni perpendicolari deve soddisfare i requisiti minimi e massimi indicati nel codice.” Già soddisfatto; non ci sono travi nelle lastre. Ok!
- “Non è consentita la ridistribuzione dei momenti negativi per codice.” Per la semplicità dell'esempio, non sarà necessario ridistribuire i momenti negativi nei solai. Ok!.
Definizione delle strisce longitudinali e trasversali
La soletta in DDM deve essere suddivisa in due fasce principali per l'analisi e la progettazione di una particolare griglia di linee: colonna e strisce centrali. La larghezza per le strisce di colonne è la minore di \({\frac {l_1}{4}}\) e \({\frac{l_2}{4}}\), dove \({l_1}\) è la lunghezza della campata lungo la griglia di linee e \({l_2}\) è la lunghezza trasversale perpendicolare.
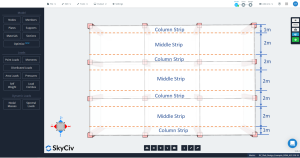
figura 3. Colonna longitudinale e strisce centrali.
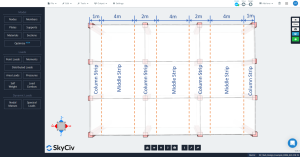
figura 4. Colonna trasversale e strisce centrali.
Spessore minimo
ACI-318 suggerisce di utilizzare l'equazione: \({t_{min}}= {\frac{l_n}{30}}={\frac{6m-0.50m}{30}}=0,1833 m = 0,20 m)
Verifica preliminare della resistenza al taglio
Prima di calcolare l'armatura in acciaio, si consiglia di verificare la capacità di taglio della soletta, uno per il taglio diretto nel collegamento e l'altro per la capacità di taglio a punzonamento sul pilastro della soletta di collegamento.
Per calcolare la domanda di taglio, usiamo i seguenti carichi gravitazionali:
- Lastra autoportante: \({SW={\gamma_c}\volte {t_{lastra}}={24 {\frac{kN}{m^3}}}\volte {0.20m}=4.8{\frac{kN}{m^2}} }\)
- Carico morto sovrapposto: \({SD={3 {\frac{kN}{m^2}}}}\)
- Carico morto totale (SW+SD): \({D={7.8 {\frac{kN}{m^2}}}}\)
- Carica in tempo reale (Occupazione residenziale) : \({L={2 {\frac{kN}{m^2}}}}\)
- Carico di forza fattorizzato (1.2D+1.6L): \({Il modulo con calcola la dimensione dell'asta di ancoraggio{u}={12.56 {\frac{kN}{m^2}}}}\)
Il primo controllo di taglio è il “raggio-taglio” genere, dove l'immagine seguente indica l'area da considerare per ottenere il taglio totale. Ispezioniamo ogni direzione, prendendo l'area più estesa.
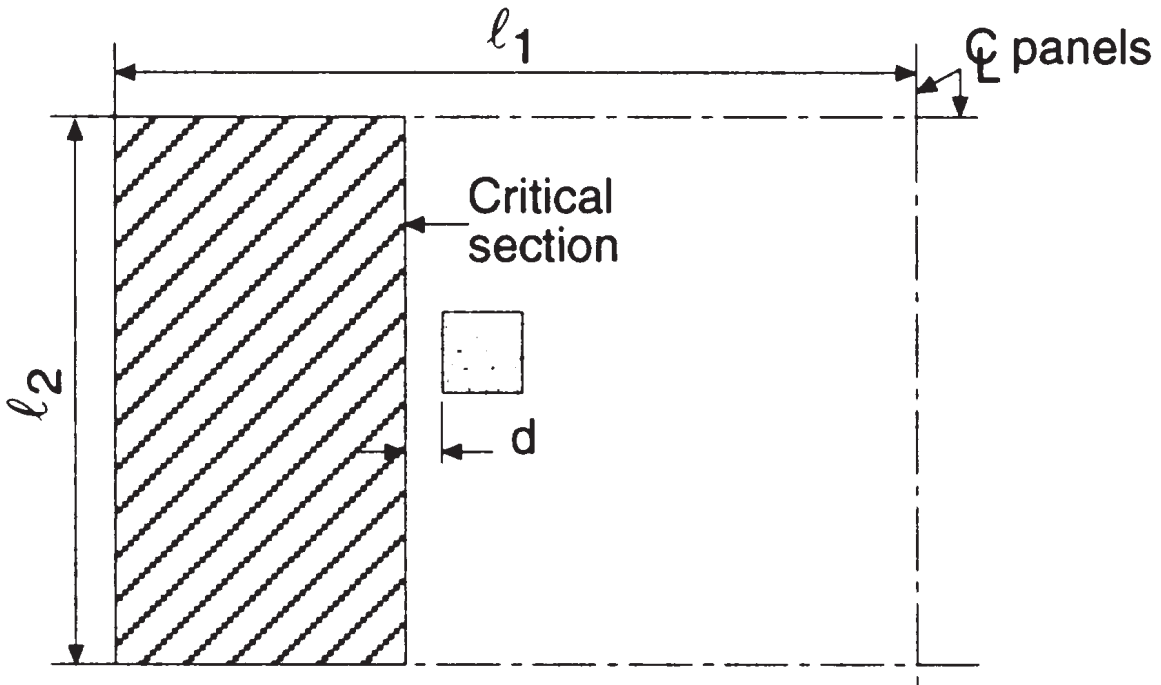
figura 5. Taglio della trave all'interno della colonna (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e progettazione del calcestruzzo strutturale”)
Dove:
- Lunghezza campata in direzione longitudinale, \({l_1 = 6,0 m }\)
- Lunghezza campata in direzione trasversale, \({l_2 = 4,0 m}\)
- Area affluente totale, taglio in direzione longitudinale \({A_t = l_2 volte (\frac{l_1}{2}-\frac{c_1}{2}-d) = 4,0 m volte (\frac{6.0m}{2}-\frac{0.50m}{2}-0.17m) = 10.32 m^2}\) (selezionato)
- Area affluente totale, taglio in direzione trasversale, \({A_t = l_1 volte (\frac{l_2}{2}-\frac{c_2}{2}-d) = 6,0 m volte (\frac{4.0m}{2}-\frac{0.50m}{2}-0.17m) = 9.48 m^2}\)
- Dimensione colonne quadrate, \({c_1 = c_2 = 0,50 m}\)
- Distanziato, \({d = h_{lastra} – copertura = 0,20 m – 0.03m = 0,17 m }\)
Pertanto, il massimo taglio della trave nella colonna interna è
\({V_u =q_uvolte A_t =12,56 {\frac{kN}{m^2}}\volte 10.32 m^2 = 129.62 kN }\)
Questo sarà confrontato con la resistenza al taglio, \({\phi_sV_c}\)
- Forza concreta, \({f'_c = 25 MPa}\)
- Resistenza dell'acciaio dell'armatura di snervamento, \({f_y = 420 MPa}\)
- \({\phi_s = 0.75}\)
- \({\phi_sV_c = 0.17phi_s lambda sqrt(f'_c) b_w d; b_w=l_2}\)
\({\phi_sV_c = 0,17volte 0,75volte 1volte sqrt(25 MPa) \volte 4000 mmvolte 170 millimetro = 433.50 kN }\)
Possiamo vedere che la resistenza al taglio è maggiore della richiesta di taglio: \({\phi_sV_c = 433.50 kN > V_u = 129.62 kN }\) Ok!.
Secondo le seguenti immagini, dobbiamo calcolare la capacità di punzonamento e la forza che deve sopportare il calcestruzzo nel collegamento interno soletta-pilastro. L'intenzione del codice nel controllare il taglio da punzonamento è di mantenere bassi i valori della sollecitazione di taglio.
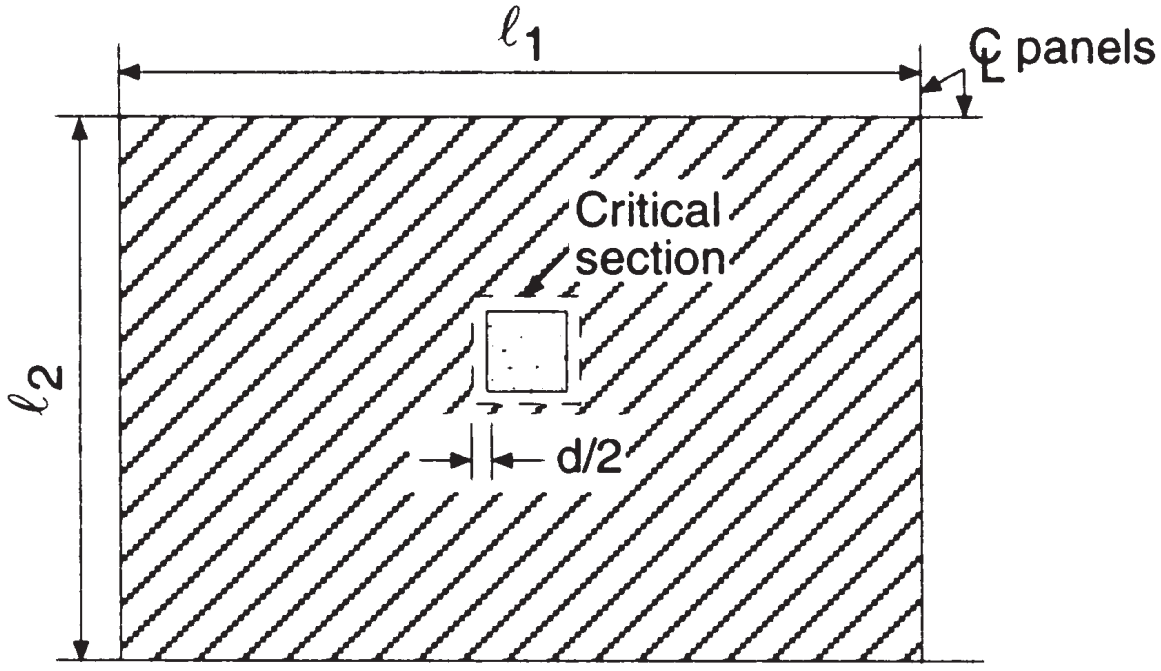
figura 6. Taglio bidirezionale alla colonna interna (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e progettazione del calcestruzzo strutturale”)
- Area affluente totale, punzonatura cesoia, \({A_t = l_1 volte l_2 – (c_1+d)^2 = 6,0 m volte 4,0 m – (0.50m+0,17 m)^2 = 23.55 m^2}\) (stessa area per entrambe le direzioni principali)
La forza di taglio totale da resistere è
\({V_u =q_uvolte A_t =12,56 {\frac{kN}{m^2}}\volte 23.55 m^2 = 295.79 kN }\)
Per ottenere la capacità di punzonamento a taglio in una soletta bidirezionale, utilizzeremo il metodo empirico stabilito dal codice ACI-318, che considera il massimo sforzo di taglio disponibile nel perimetro effettivo in corrispondenza della sezione critica. L'espressione più conservativa per la colonna interna è
- Capacità di punzonatura, \({\phi_sV_c = 0.33phi_s lambda sqrt(f'_c) b_0 d; b_0=4volte (c_1+d)}\)
Pertanto, abbiamo la resistenza al taglio di
\({\phi_sV_c = 0,33volte 0.75 \volte 1 \sqrt(25 MPa) \volte (4\volte (500 mm+170 mm)\volte 170 mm) = 563.81 kN }\)
Possiamo vedere che la resistenza al taglio è maggiore della richiesta di taglio: \({\phi_sV_c = 563.81 kN > V_u = 295.75 kN }\) Ok!.
Abbiamo verificato le richieste di taglio uno e bidirezionale alla connessione interna della colonna. A causa del fatto che entrambe le richieste sono inferiori alle rispettive capacità o resistenze, passeremo ora a calcolare l'armatura principale dell'armatura per la flessione della soletta.
Se sei nuovo in SkyCiv, Iscriviti e testa tu stesso il software!
Momento statico totale per campata.
Il momento massimo che può essere sviluppato in una doppia trave ad estremità fissa è un momento isostatico pari a \({M = frac{wvolte {l_1}^ 2}{8}}\) (Guarda la figura 6).
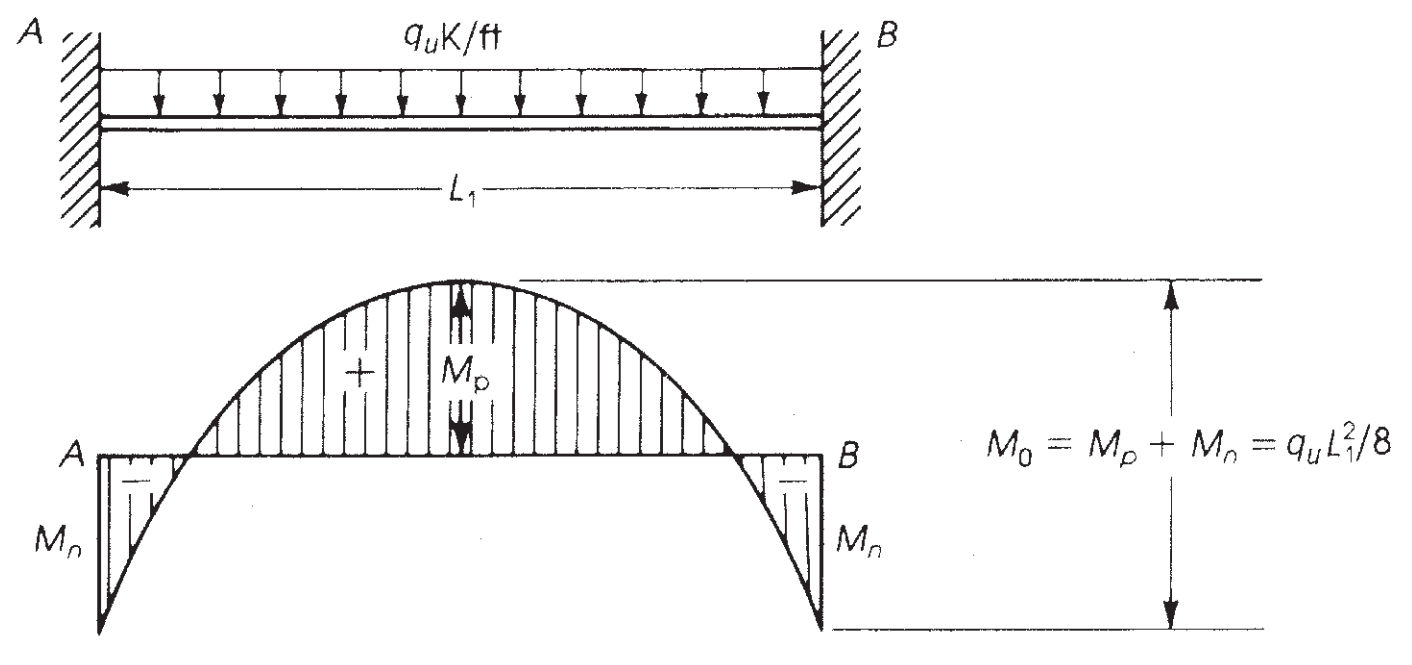
figura 7. Momento flettente in una trave ad estremità fissa. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e progettazione del calcestruzzo strutturale”)
ACI-18 prende questo principio e, per il metodo di progettazione diretta (DDM), stabilisce il momento statico massimo da considerare per campata \({M_0}\)
Direzione longitudinale:
- \({M_0 = frac {q_uvolte l_2volte {l_{n,1}}^ 2}{8}}\)
- \({M_0 = frac {12.56 {\frac{kN}{m^2}}\volte 4,0 mvolte (6m-0.50m)^ 2}{8}=189,97 kN-m}\)
Direzione trasversale:
- \({M_0 = frac {q_uvolte l_1volte {l_{n,2}}^ 2}{8}}\)
- \({M_0 = frac {12.56 {\frac{kN}{m^2}}\volte 6,0 mvolte (4m-0.50m)^ 2}{8}=115,40 kN-m}\)
Il passo successivo è assegnare questo momento totale considerando il tipo di pannello, interno o esterno. (Guarda la figura 7). Dopo di che, perché le campate sono continue, è necessario dividere anche il momento in positivo e negativo. Quest'ultimo è mostrato nelle immagini 8 e 9.
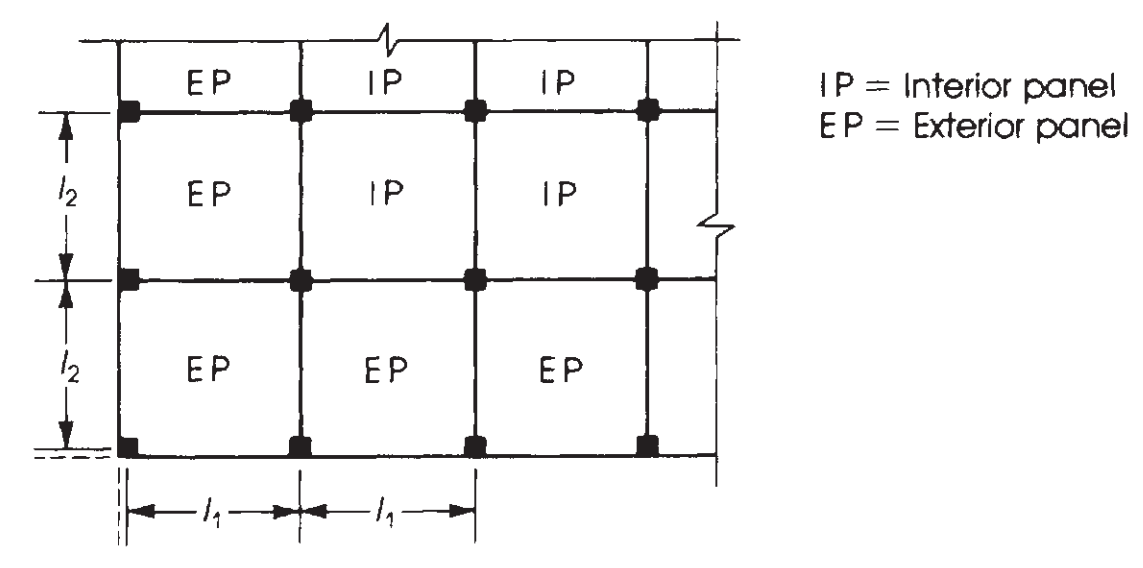
figura 8. Definizione dei pannelli in base alla loro posizione relativa in una pianta del solaio. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e progettazione del calcestruzzo strutturale”)
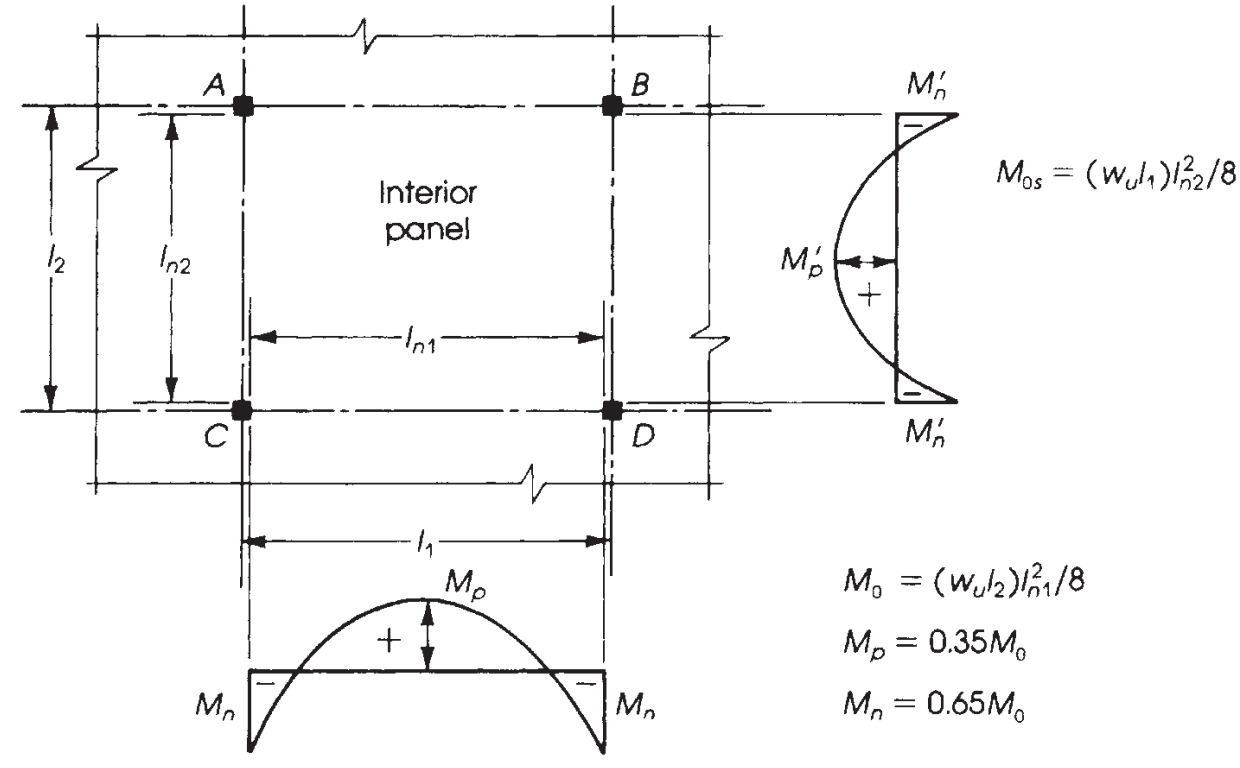
figura 9. Distribuzione dei momenti in un pannello interno. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e progettazione del calcestruzzo strutturale”)
È fondamentale conoscere la corretta distribuzione dei momenti in funzione del solaio che stiamo progettando. In questo esempio, abbiamo l'ultimo caso nell'immagine seguente (figura 9), “Niente travi,” applicato a soletta piana o soletta piena senza alcuna trave, né sul bordo né tra i supporti.
La differenza principale nei cinque casi mostrati in figura 9 è la frazione di momento da assegnare sui pannelli esterni, in cui il vincolo relativo alla fine cambia i valori da calcolare.
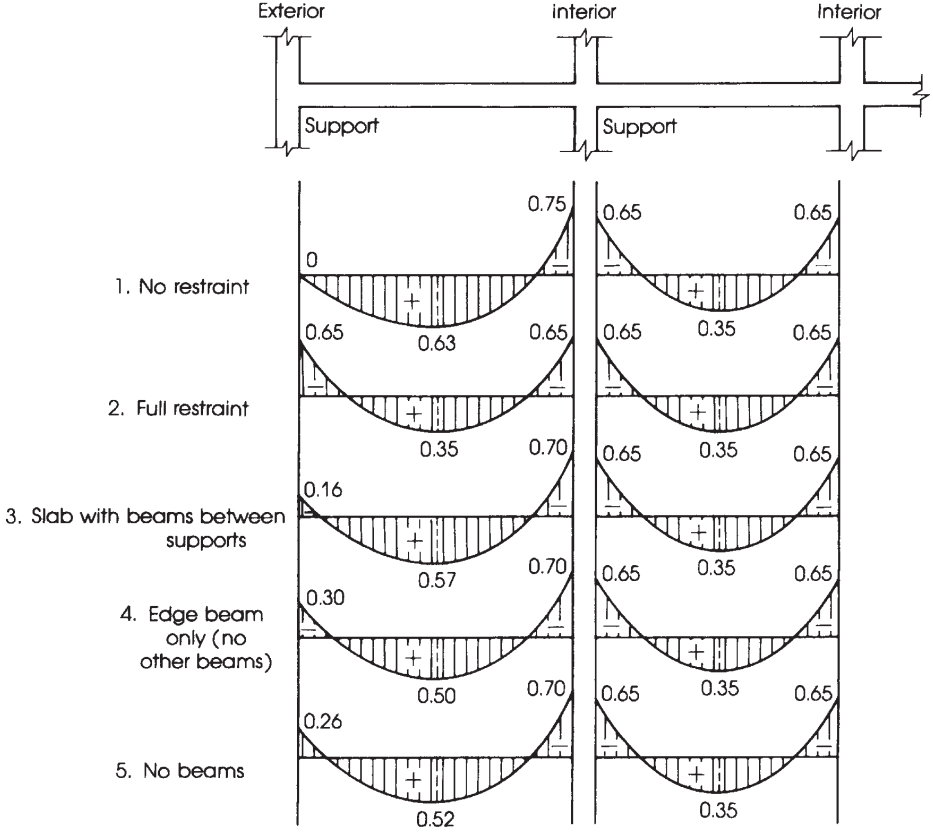
figura 10. Distribuzione del momento statico totale in momenti campate negativi e positivi. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e progettazione del calcestruzzo strutturale”)
Distribuzione del momento totale fattorizzato \({M_0}\) per arco in momenti negativi e positivi.
Una volta \({M_0}\) è stato calcolato, è il momento di assegnare la frazione di momenti in positivo e negativo in ogni striscia del disegno, questo è, colonna e strisce centrali. Per maggiore chiarezza, figura 10 aiuta a specificare il fattore appropriato da considerare nella distribuzione del momento totale.
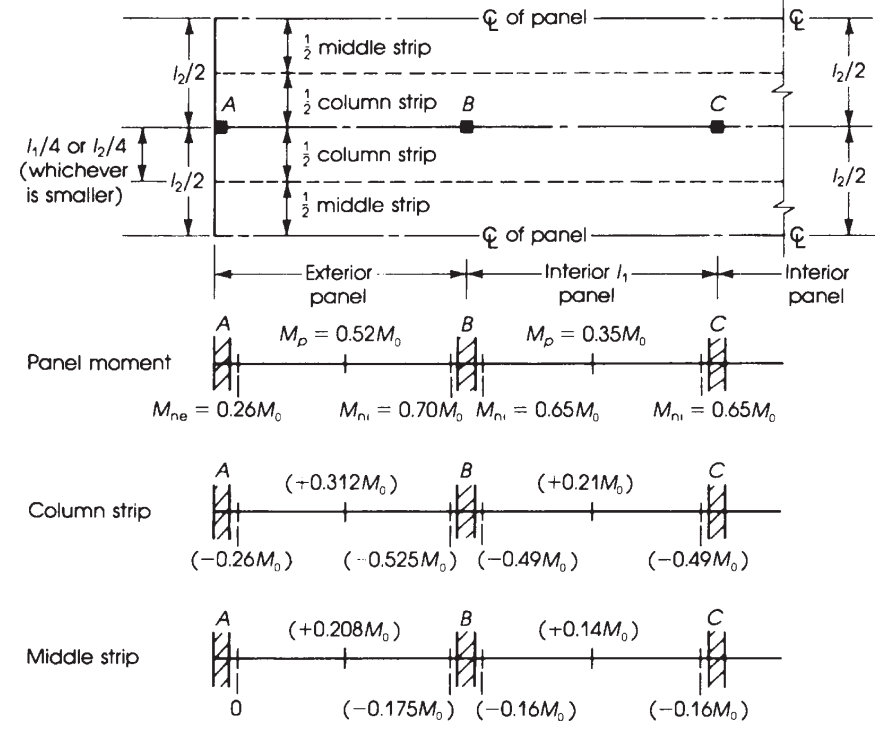
figura 11. Larghezza del telaio rigido equivalente e distribuzione dei momenti nelle solette piane. (Nadim Hassoun e Akthem AI-Manaseer, “Teoria e progettazione del calcestruzzo strutturale”)
Utilizzando i precedenti fattori indicati in figura 10, otteniamo nella tabella seguente il momento ultimo.
Direzione longitudinale: \({M_0 = 189.97 kN-m}\)
| intervallo (ES:Esterno, È:Interni) | Momento totale (kN-m) | Momento strisciante della colonna (kN-m) | Momento centrale della striscia (kN-m) |
|---|---|---|---|
| Esterno negativo ES | 0.26M0=49.39 | 0.26M0=49.39 | 0 |
| ES positivo | 0.52M0=98,78 | 0.31M0=58,89 | 0.21M0=39,89 |
| Interno negativo ES | 0.70M0=132,98 | 0.53M0=100,68 | 0.17M0=32.29 |
| SI positivo | 0.35M0=66,49 | 0.21M0=39,89 | 0.14M0=26,60 |
| È negativo | 0.65M0=123,48 | 0.49M0=93.09 | 0.16M0=30.40 |
Con il momento una volta distribuito, è il momento di determinare l'armatura in acciaio da posizionare nella soletta. Svilupperemo solo un calcolo e poi tutti i risultati in una tabella.
Momento nella campata esterna negativa nella striscia di colonne, \({M_u = 49.39 kN-m}\)
- Presunta sezione a tensione controllata. \({\fi_f = 0.9}\)
- Larghezza della striscia della colonna, \({b=2.0 m}\)
- Zona di rinforzo in acciaio, \({A_s = frac{M_u}{\phi_fvolte 0.9dvolte fy}= frac{49.39kN-m}{0.9\volte 0.9(0.17m)\volte 420 MPa}=853,996 {mm}^ 2}\)
- \({\rho_{min} = 0.0018}\). Area minima di armatura in acciaio, \({UN_{S,min}=rho_{min}\volte bvolte d = 0.0018 \volte 2,0 m volte 0,17 m =612 {mm}^ 2}\). Adesso, controllare se la sezione si comporta come a tensione controllata.
- \({a = frac{A_stime f_y}{0.85\volte f'cvolte b} = frac{853.996 {mm}^2volte 420 MPa}{0.85\volte 25 MPavolte 2,0 m }= 8.439 mm}\)
- \({c = frac{un carico}{\beta_1}= Frac{8.439 mm}{0.85} = 9,929 mm }\)
- \({\varepsilon_t = (\frac{0.003}{c})\volte d – 0.003 = (\frac{0.003}{9.929mm})\volte 170 mm – 0.003 = 0.048 > 0.005 }\) Ok!, è una sezione a tensione controllata!.
| intervallo(ES:Esterno, È:Interni) | Momento della striscia di colonna (kN-m) | \({UN_{S,cal} ({mm}^ 2)}\) | \({UN_{S,min} ({mm}^ 2)}\) | \({un carico (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Esterno negativo ES | 49.39 | 853.996 | 612.0 | 8.439 | 9.929 | 0.048 > 0.005! |
| ES positivo | 58.89 | 1018.259 | 612.0 | 10.063 | 11.839 | 0.040 > 0.005! |
| Interno negativo ES | 100.68 | 1740.844 | 612.0 | 17.204 | 20.24 | 0.022 > 0.005! |
| SI positivo | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.06 > 0.005! |
| È negativo | 93.09 | 1609.607 | 612.0 | 15.907 | 18.714 | 0.024 > 0.005! |
Momento nell'intervallo positivo esterno nella striscia centrale, \({M_u = 39.89 kN-m}\)
- Presunta sezione a tensione controllata. \({\fi_f = 0.9}\)
- Larghezza striscia centrale, \({b=2.0 m}\)
- Zona di rinforzo in acciaio, \({A_s = frac{M_u}{\phi_fvolte 0.9dvolte fy}= frac{39.89kN-m}{0.9\volte 0.9(0.17m)\volte 420 MPa}=689.733 {mm}^ 2}\)
- \({\rho_{min} = 0.0018}\). Area minima di armatura in acciaio, \({UN_{S,min}=rho_{min}\volte bvolte d = 0.0018 \volte 2,0 m volte 0,17 m =612 {mm}^ 2}\). Adesso, controllare se la sezione si comporta come a tensione controllata.
- \({a = frac{A_stime f_y}{0.85\volte f'cvolte b} = frac{689.766 {mm}^2volte 420 MPa}{0.85\volte 25 MPavolte 2,0 m }= 6.816 mm}\)
- \({c = frac{un carico}{\beta_1}= Frac{6.816 mm}{0.85} = 8.019 mm }\)
- \({\varepsilon_t = (\frac{0.003}{c})\volte d – 0.003 = (\frac{0.003}{8.019mm})\volte 170 mm – 0.003 = 0.0605 > 0.005 }\) Ok!, è una sezione a tensione controllata!.
| intervallo(ES:Esterno, È:Interni) | Momento centrale della striscia (kN-m) | \({UN_{S,cal} ({mm}^ 2)}\) | \({UN_{S,min} ({mm}^ 2)}\) | \({un carico (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Esterno negativo ES | 0 | 0.00 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| ES positivo | 39.89 | 689.733 | 612.0 | 6.816 | 8.019 | 0.061 > 0.005! |
| Interno negativo ES | 32.29 | 558.322 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| SI positivo | 26.60 | 459.937 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| È negativo | 30.40 | 525.642 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
Direzione trasversale: \({M_0 = 115.40 kN-m}\)
| intervallo (ES:Esterno, È:Interni) | Momento totale (kN-m) | Momento strisciante della colonna (kN-m) | Momento centrale della striscia (kN-m) |
|---|---|---|---|
| Esterno negativo ES | 0.26M0=30.00 | 0.26M0=30.00 | 0 |
| ES positivo | 0.52M0=60,00 | 0.31M0=35,77 | 0.21M0=24.23 |
| Interno negativo ES | 0.70M0=80,78 | 0.53M0=61.16 | 0.17M0=19.62 |
| SI positivo | 0.35M0=40.39 | 0.21M0=24.23 | 0.14M0=16.16 |
| È negativo | 0.65M0=75.01 | 0.49M0=56,55 | 0.16M0=18.46 |
Con il momento una volta distribuito, è il momento di determinare l'armatura in acciaio da posizionare nella soletta. Svilupperemo solo un calcolo e poi tutti i risultati in una tabella.
Momento nella campata esterna negativa nella striscia di colonne, \({M_u = 30.00 kN-m}\)
- Presunta sezione a tensione controllata. \({\fi_f = 0.9}\)
- Larghezza della striscia della colonna, \({b=2.0 m}\)
- Zona di rinforzo in acciaio, \({A_s = frac{M_u}{\phi_fvolte 0.9dvolte fy}= frac{30.00kN-m}{0.9\volte 0.9(0.17m)\volte 420 MPa}=518,726 {mm}^ 2}\)
- \({\rho_{min} = 0.0018}\). Area minima di armatura in acciaio, \({UN_{S,min}=rho_{min}\volte bvolte d = 0.0018 \volte 2,0 m volte 0,17 m =612 {mm}^ 2}\). Adesso, controllare se la sezione si comporta come a tensione controllata.
- \({a = frac{A_stime f_y}{0.85\volte f'cvolte b} = frac{518.726 {mm}^2volte 420 MPa}{0.85\volte 25 MPavolte 2,0 m }= 6.048 mm}\)
- \({c = frac{un carico}{\beta_1}= Frac{6.048 mm}{0.85} = 7,115 mm }\)
- \({\varepsilon_t = (\frac{0.003}{c})\volte d – 0.003 = (\frac{0.003}{7.115mm})\volte 170 mm – 0.003 = 0.069 > 0.005 }\) Ok!, è una sezione a tensione controllata!.
| intervallo(ES:Esterno, È:Interni) | Momento della striscia di colonna (kN-m) | \({UN_{S,cal} ({mm}^ 2)}\) | \({UN_{S,min} ({mm}^ 2)}\) | \({un carico (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Esterno negativo ES | 30.00 | 518.726 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| ES positivo | 35.77 | 618.494 | 612.0 | 6.112 | 7.191 | 0.068 > 0.005! |
| Interno negativo ES | 61.16 | 1057.509 | 612.0 | 10.451 | 12.295 | 0.038 > 0.005! |
| SI positivo | 24.23 | 418.958 | 612.0 | 6.048 | 7.115 | 0.069 > 0.005! |
| È negativo | 56.55 | 977.799 | 612.0 | 9.663 | 11.368 | 0.042 > 0.005! |
Momento nell'intervallo positivo esterno nella striscia centrale, \({M_u = 24.23 kN-m}\)
- Presunta sezione a tensione controllata. \({\fi_f = 0.9}\)
- Larghezza della striscia della colonna, \({b=4.0 m}\)
- Zona di rinforzo in acciaio, \({A_s = frac{M_u}{\phi_fvolte 0.9dvolte fy}= frac{24.23 kN-m}{0.9\volte 0.9(0.17m)\volte 420 MPa}=418.958 {mm}^ 2}\)
- \({\rho_{min} = 0.0018}\). Area minima di armatura in acciaio, \({UN_{S,min}=rho_{min}\volte bvolte d = 0.0018 \volte 4,0 m volte 0,17 m = 1224 {mm}^ 2}\). Adesso, controllare se la sezione si comporta come a tensione controllata.
- \({a = frac{A_stime f_y}{0.85\volte f'cvolte b} = frac{1224 {mm}^2volte 420 MPa}{0.85\volte 25 MPavolte 4,0 m }= 6.048 mm}\)
- \({c = frac{un carico}{\beta_1}= Frac{6.048 mm}{0.85} = 7.115 mm }\)
- \({\varepsilon_t = (\frac{0.003}{c})\volte d – 0.003 = (\frac{0.003}{7.115mm})\volte 170 mm – 0.003 = 0.069 > 0.005 }\) Ok!, è una sezione a tensione controllata!.
| intervallo(ES:Esterno, È:Interni) | Momento centrale della striscia (kN-m) | \({UN_{S,cal} ({mm}^ 2)}\) | \({UN_{S,min} ({mm}^ 2)}\) | \({un carico (mm)}\) | \({c (mm)}\) | \({\varepsilon_t > 0.005}\) |
|---|---|---|---|---|---|---|
| Esterno negativo ES | 0.00 | 0.00 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| ES positivo | 24.23 | 418.958 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| Interno negativo ES | 19.62 | 339.247 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| SI positivo | 16.16 | 279.420 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
| È negativo | 18.46 | 319.189 | 1224.00 | 6.048 | 7.115 | 0.069 > 0.005! |
Se sei nuovo in SkyCiv, Iscriviti e testa tu stesso il software!
Modulo di progettazione SkyCiv S3D
In questa sezione, descriviamo il risultato del progetto utilizzando il modulo per il design della piastra incluso in SkyCiv. Non spieghiamo come modellare e analizzare la struttura (per questi, vedere gli articoli correlati su questo argomento nella nostra documentazione: Come modellare una struttura in SkyCiv?, Come applicare i carichi nel mio modello di edificio? e Come eseguire un'analisi elastica lineare?)
È conveniente applicare una maglia fine alle lastre per ottenere un risultato di progettazione accurato. Si prega di dare un'occhiata alla seguente immagine per maggiore chiarezza.
figura 12. Maglia più fine applicata alle lastre
Il passaggio successivo consiste nell'eseguire il modulo di progettazione e selezionare le opzioni che calcolano un'area di armatura in acciaio ottimizzata.
figura 13. Definizione delle proprietà del calcestruzzo della soletta prima dell'ottimizzazione del progetto.
figura 14 rappresenta l'orientamento degli assi locali della piastra. Perché asse locale 3 è verso il basso, il “superiore” è il fondo, che per il “parte inferiore” sarà il top, prendendo così correttamente i dati dal progetto.
Un altro dato importante è la dimensione delle maglie della soletta; è un elemento quadrato in lamiera con dimensioni in pianta di 500mm x 500mm. SkyCiv S3D fornisce l'area di rinforzo come valore integrato per elemento finito. così, se vogliamo ottenere l'area totale dell'armatura di una colonna o fascia centrale, dobbiamo calcolare il valore medio dal numero di elementi che sommano la larghezza della striscia che si sta analizzando. Per esempio, per la striscia di colonne, verranno presi in considerazione quattro elementi (4×0.5m = 2 m).
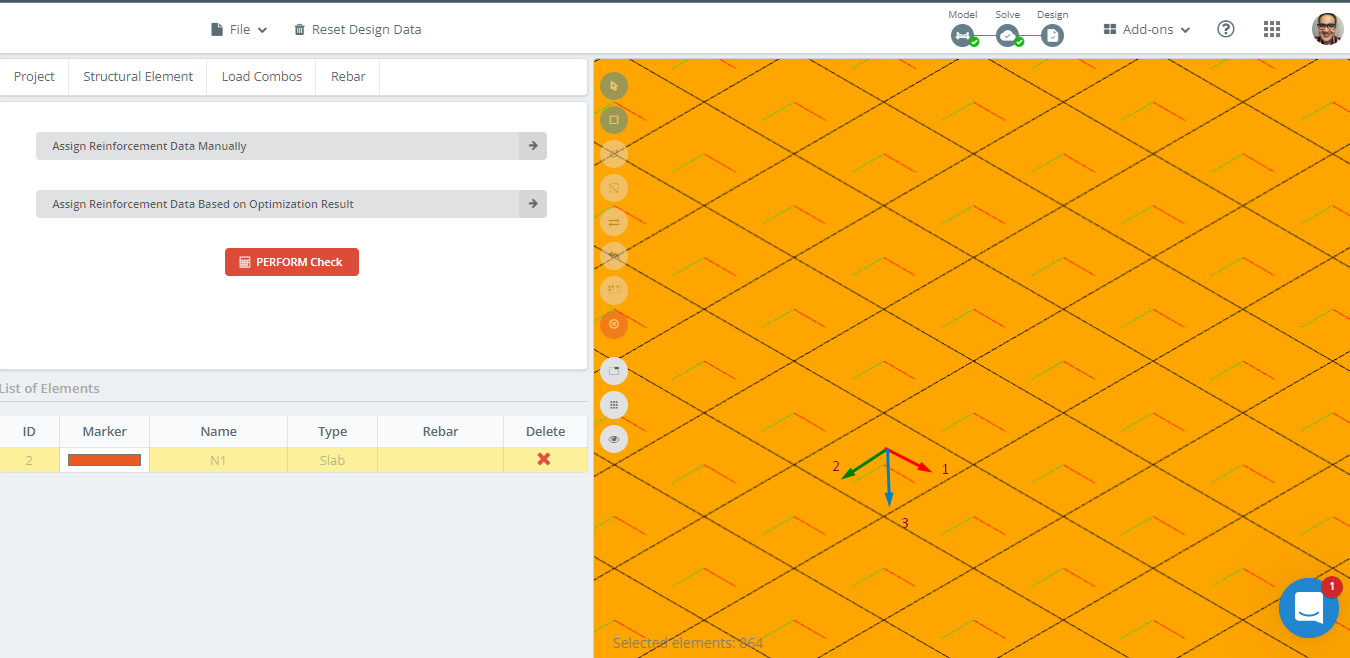
figura 14. Orientamento degli assi locali nell'esempio del solaio.
Primo, analizziamo l'area di armatura richiesta lungo la direzione longitudinale in asse 1.
Striscia di colonne
- Momento esterno negativo (rinforzo superiore): \({UN_{S,superiore} =(119.09\volte 2 + 952.72 + 833.64 )\frac{{mm}^ 2}{m} \volte 0,50 m = 1012.27 {mm}^ 2}\)
- Momento esterno positivo (rinforzo inferiore): \({UN_{S,bot} = 4*463.90 \frac{{mm}^ 2}{m}\volte 0,50 m = 927.80 {mm}^ 2}\)
- Momento negativo esterno interno (rinforzo superiore): \({UN_{S,superiore} =(1071.82\volte 2 +714.54 \volte 2 )\frac{{mm}^ 2}{m} \volte 0,50 m = 1786.36 {mm}^ 2}\)
- Momento interno positivo(rinforzo inferiore): \({UN_{S,bot} = 4*309.27 \frac{{mm}^ 2}{m}\volte 0,50 m = 618.54 {mm}^ 2}\)
- Momento interno negativo (rinforzo superiore): \({UN_{S,superiore} =(714.54\volte 2 +952.73 \volte 2 )\frac{{mm}^ 2}{m} \volte 0,50 m = 1667.27 {mm}^ 2}\)
Striscia di Mezzo
- Momento esterno negativo (rinforzo superiore): \({UN_{S,superiore} =(119.09\volte 4)\frac{{mm}^ 2}{m} \volte 0,50 m = 238.18 {mm}^ 2}\)
- Momento esterno positivo (rinforzo inferiore): \({UN_{S,bot} = (463.90\volte 2 +412.36 \volte 2 ) \frac{{mm}^ 2}{m}\volte 0,50 m = 876.26 {mm}^ 2}\)
- Momento negativo esterno interno (rinforzo superiore): \({UN_{S,superiore} =(357.27\volte 2 +476.36 \volte 2 )\frac{{mm}^ 2}{m} \volte 0,50 m = 833.63 {mm}^ 2}\)
- Momento interno positivo(rinforzo inferiore): \({UN_{S,bot} = 4*257.72 \frac{{mm}^ 2}{m}\volte 0,50 m = 515.44 {mm}^ 2}\)
- Momento interno negativo (rinforzo superiore): \({UN_{S,superiore} =(357.27\volte 2 +476.36 \volte 2 )\frac{{mm}^ 2}{m} \volte 0,50 m = 833.63 {mm}^ 2}\)
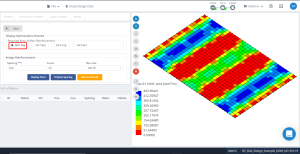
figura 15. Risultati di ottimizzazione in direzione “1” e il lato superiore (Il fondo, in realtà).
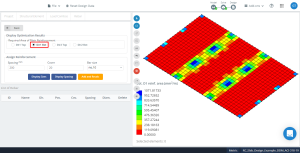
figura 16. Risultati di ottimizzazione in direzione “1” e il lato inferiore (Lato superiore, in realtà).
Infine, analizziamo l'area di armatura richiesta lungo la direzione trasversale in asse 2.
Striscia di colonne
- Momento esterno negativo (rinforzo superiore): \({UN_{S,superiore} =(91.55\volte 2 + 457.73 + 549.28 )\frac{{mm}^ 2}{m} \volte 0,50 m = 595.055 {mm}^ 2}\)
- Momento esterno positivo (rinforzo inferiore): \({UN_{S,bot} = (269.68\volte 3+239.72) \frac{{mm}^ 2}{m}\volte 0,50 m = 524.38 {mm}^ 2}\)
- Momento negativo esterno interno (rinforzo superiore): \({UN_{S,superiore} =(823.92\volte 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \volte 0,50 m = 1327.43 {mm}^ 2}\)
- Momento interno positivo(rinforzo inferiore): \({UN_{S,bot} = (179.79\volte 3+149.82) \frac{{mm}^ 2}{m}\volte 0,50 m = 344.60 {mm}^ 2}\)
- Momento interno negativo (rinforzo superiore): \({UN_{S,superiore} =(823.92\volte 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \volte 0,50 m = 1327.43 {mm}^ 2}\)
Striscia di Mezzo
- Momento esterno negativo (rinforzo superiore): \({UN_{S,superiore} =(183.09\volte 2+91.55volte 6)\frac{{mm}^ 2}{m} \volte 0,50 m = 457.74 {mm}^ 2}\)
- Momento esterno positivo (rinforzo inferiore): \({UN_{S,bot} = (209.75\volte 2 +179.79 \volte 2 +149.82 \volte 4) \frac{{mm}^ 2}{m}\volte 0,50 m = 689.18{mm}^ 2}\)
- Momento negativo esterno interno (rinforzo superiore): \({UN_{S,superiore} =(274.64\volte 2+91.55volte 6)\frac{{mm}^ 2}{m} \volte 0,50 m = 549.29 {mm}^ 2}\)
- Momento interno positivo(rinforzo inferiore): \({UN_{S,bot} = (119.86\volte 4 + 89.89\volte 4) \frac{{mm}^ 2}{m}\volte 0,50 m = 419.50 {mm}^ 2}\)
- Momento interno negativo (rinforzo superiore): \({UN_{S,superiore} =(274.64\volte 2+91.55volte 6 )\frac{{mm}^ 2}{m} \volte 0,50 m = 549.29 {mm}^ 2}\)
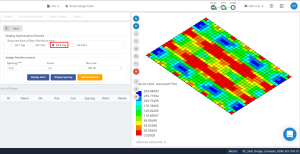
figura 17. Risultati di ottimizzazione in direzione “2” e il lato superiore (Il fondo, in realtà).
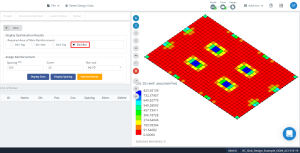
figura 18. Risultati di ottimizzazione in direzione “2” e il lato inferiore (Lato superiore, in realtà).
Confronto dei risultati
La tabella seguente mostra i risultati per il DDM (“Metodo di progettazione diretta”) e l'ottimizzazione dell'armatura in acciaio S3D.
| intervallo (ES:Esterno, È:Interni) | Striscia di colonne (Progettazione S3D) \({Come ({mm}^ 2)}\) | Striscia di colonne (ACI-318 DDM) \({Come ({mm}^ 2)}\) | % dif | Striscia di Mezzo (Progettazione S3D) \({Come ({mm}^ 2)}\) | Striscia di Mezzo (ACI-318 DDM) \({Come ({mm}^ 2)}\) | % dif |
|---|---|---|---|---|---|---|
| Esterno negativo ES | 1012.27 | 853.996 | 15.636 | 238.18 | 0 (612.0) | 100.00 |
| ES positivo | 927.80 | 1018.259 | 9.75 | 876.26 | 689.733 | 21.287 |
| Interno negativo ES | 1786.36 | 1740.844 | 2.48 | 833.63 | 558.322 (612.0) | 26.586 |
| SI positivo | 618.54 | 689.733 | 11.51 | 515.44 | 459.937 (612.0) | 18.734 |
| È negativo | 1667.27 | 1609.607 | 3.459 | 833.63 | 525.642 (612.0) | 26.586 |
Direzione trasversale
| intervallo (ES:Esterno, È:Interni) | Striscia di colonne (Progettazione S3D) \({Come ({mm}^ 2)}\) | Striscia di colonne (ACI-318 DDM) \({Come ({mm}^ 2)}\) | % dif | Striscia di Mezzo (Progettazione S3D) \({Come ({mm}^ 2)}\) | Striscia di Mezzo (ACI-318 DDM) \({Come ({mm}^ 2)}\) | % dif |
|---|---|---|---|---|---|---|
| Esterno negativo ES | 595.055 | 518.726 | 12.827 | 457.74 | 0 (1224) | 100.00 |
| ES positivo | 524.38 | 618.494 | 17.948 | 689.18 | 418.958 | 39.209 |
| Interno negativo ES | 1327.43 | 1057.509 | 20.334 | 549.29 | 339.247 | 38.239 |
| SI positivo | 344.60 | 418.958 | 21.578 | 419.50 | 279.42 | 33.392 |
| È negativo | 1327.43 | 977.799 | 26.339 | 549.29 | 319.189 | 41.891 |
Conclusione
Abbiamo dimostrato in questo articolo che il modulo SkyCiv per la progettazione della piastra calcola l'armatura in acciaio per la flessione della lastra in base al codice ACI-318-19. Confronto dei risultati dell'analisi nelle strisce di colonna, dove a causa della loro rigidità relativa, i momenti sono molto concentrati, le differenze tra i calcoli manuali e l'ottimizzazione di S3D arrotondano un valore di 10 – 15%. Questa praticità indica un'ottima corrispondenza tra le procedure di analisi e progettazione.
Per strisce centrali, i risultati differiscono un po' di più perché il codice assegna solo il resto del momento dopo aver preso le strisce di colonna corrispondenti. Ciò avrà un impatto sulla partita quando la confrontiamo con l'analisi del software, che è più preciso.
Nuovo su SkyCiv? Iscriviti e prova tu stesso il software!


