Momento libero di inerzia e calcolatore centroide
Calcola il Momento d'inerzia, Centroide, e il Modulo di Sezione per un'ampia varietà di forme
Una guida completa al nostro calcolatore del momento d'inerzia
Il calcolatore del Momento d’inerzia e Centroide SkyCiv aiuta a determinare il momento di inerzia, il centroide, e altre importanti proprietà geometriche per una varietà di forme, tra cui rettangoli, cerchi, sezioni cave, triangoli, I-Beam, T-Beam, angoli e scanalature. Abbiamo anche alcuni articoli qui in basso su come calcolare il momento di inerzia, così come ulteriori informazioni sui centroidi e modulo di sezione.
Puoi risolvere fino a tre sezioni prima che ti venga richiesto di registrarti per un account gratuito - che ti dà anche accesso a più software e risultati. L’account a pagamento mostrerà tutti i calcoli di mano su come lo strumento è arrivato a questo risultato. Per maggiori informazioni su questo argomento, fare riferimento al calcolatore e ai link ad altri utili strumenti e funzionalità che SkyCiv può offrire.
Come usare il Calcolatore del Momento d'inerzia SkyCiv
Guarda il video demo qui sotto per iniziare con il nostro calcolatore.
Basta scegliere la forma della sezione trasversale che si desidera valutare dall'elenco a tendina, inserire le dimensioni della sezione scelta e fare clic su Calcola.
Questo calcolatore multiuso gratuito è tratto dalla nostra suite completa Software di analisi strutturale. Consente di:
- Calcolare il momento di inerzia (I) di una sezione della trave (secondo momento di area)
- Calcolatore del centroide utilizzato per calcolare il centroide (C) negli assi X e Y di una sezione della trave
- Calcolare il primo momento di area (Momento statico di inerzia) (Q) di una sezione della trave
- Un calcolatore del modulo di sezione per calcolare il modulo di sezione (Z) di una sezione della trave
- Calcolare la costante di torsione (J) di una sezione della trave
Definizioni di proprietà della sezione comune
Il calcolatore del momento d'inerzia calcolerà accuratamente una serie di importanti proprietà di sezione utilizzate nell'ingegneria strutturale. Ecco un elenco conciso dei termini e delle definizioni delle proprietà della sezione:
- Area della sezione (A) – Area della sezione è un calcolo abbastanza semplice, ma direttamente utilizzato nei calcoli delle sollecitazioni assiali (più area della sezione trasversale, più forza assiale)
- Momento d'inerzia (lz, Iy) - noto anche come secondo momento di area, è un calcolo utilizzato per determinare la forza di un membro e la sua resistenza contro la deflessione. Più alto è questo numero, più forte è la sezione. Ci sono due assi:
- Asse maggiore (lz) – Questo è l'asse Z ed è in genere considerato l'asse maggiore in quanto di solito è la direzione più forte del membro.
- Asse minore (Iy) - Si tratta dell'asse Y ed è considerato l'asse minore o debole. Questo perché le sezioni non sono progettate per prendere tanta forza su questo asse
- ● Vale anche la pena notare che se una forma ha le stesse dimensioni in entrambe le direzioni (quadrato, circolare ecc..) questi valori saranno gli stessi in entrambe le direzioni. Vedere Momento di Inerzia di un cerchio per saperne di più.
- Centroide (Cz, Cy) - questo è il centro di massa per la sezione e di solito ha una componente Z e Y. Per le forme simmetriche, questo sarà il centro geometrico. Per le forme non simmetriche (come un angolo, o scanalatura) queste saranno in posizioni diverse. Scopri come calcolare il centroide di una sezione della trave. La calcolatrice di cui sopra funge anche da calcolatrice centroide, calcolando il centroide X e Y di qualsiasi tipo di forma.
- Momento statico di inerzia (Qz, Qy) - Conosciuto anche come primo momento di area, questo misura la distribuzione dell'area della sezione della trave da un asse. Come il Momento d'Inerzia, questi sono in entrambe le direzioni Z e Y. Questi sono usati tipicamente nei calcoli di sforzo di taglio, in modo che più grande questo valore è, più forte la sezione è contro il taglio. La calcolatrice fornirà questo valore, ma clicca qui per saperne di più sul calcolo del primo momento dell'area.
- Modulo di sezione elastica (Sz, Sy in America. Zz, Zy in Gran Bretagna o in Australia) – Conosciuto anche come modulo di sezione statica, e viene utilizzato nei calcoli delle sollecitazioni di flessione. Di solito sono calcolati per la sezione superiore e inferiore delle fibre. Ad esempio, Szt è il modulo di sezione sull'asse Z alla fibra superiore della sezione.
- Costante di torsione (J) - noto anche come momento polare di inerzia o J, è un valore che descrive la resistenza di un materiale alla torsione o deformazione torsionale.
- Il modulo di sezione plastica (S) - una misura della capacità di una forma a sezione trasversale di resistere alla flessione plastica, utilizzata per stimare lo stress di un materiale quando inizia a cedere (raggiunge il suo limite di plasticità) sotto un carico specifico ed è tipicamente utilizzato per la progettazione e l'analisi di travi sotto carico.
Altri parametri - Questi sono i risultati più avanzati calcolati dall'intero Costruttore di Sezioni SkyCiv:
- Prodotto di inerzia (circa asse Z e asse Y): misura della resistenza di una forma alla rotazione attorno a un asse specifico, uguale al prodotto trasversale della distanza dall'asse a qualsiasi punto della forma e alla componente corrispondente del momento di inerzia del punto.
- Modulo di sezione plastica (circa asse Z e asse Y): misura della capacità di una forma di sezione trasversale di resistere alla flessione plastica, utilizzata per stimare lo stress di un materiale quando inizia a cedere (raggiunge il suo limite di plasticità) sotto un carico specifico.
- Asse neutro plastico (circa asse Z e asse Y): un asse a sezione trasversale attraverso il quale devono passare tutte le forze che agiscono sulla forma per provocare la deformazione plastica.
- Area di taglio (circa asse Z e asse Y): l'area di una forma di sezione trasversale che è efficace nel resistere alle forze di taglio.
- Distanza tra centro di taglio e centroide (sia nell'asse Z che nell'asse Y): il calcolatore di centroidi SkyCiv aiuta a calcolare la distanza tra il centro di taglio e il centroide di una forma trasversale.
- Costante di torsione (facendo uso di FEA): un valore che descrive la resistenza del materiale alla torsione o alla deformazione torsionale, calcolata facendo uso dell'analisi finita dell'elemento.
- Raggio di torsione: la distanza da un asse in cui l'area di una forma trasversale deve essere concentrata per ottenere la stessa costante di torsione della forma reale.
- Costante di deformazione: un valore che descrive la resistenza di un materiale alla deformazione o distorsione.
- Costante di monosimmetria (circa asse Z e asse Y): misura di come la forma di una sezione trasversale è simmetrica rispetto a un asse specifico, con un valore di zero che indica la simmetria perfetta.
- Raggio di rotazione (circa asse Z e asse Y): distanza da un asse alla quale deve essere concentrata l'area di una forma della sezione trasversale per ottenere lo stesso momento di inerzia della forma reale.
- Angolo di rotazione dell'asse principale: l'angolo tra l'asse neutro e l'asse principale di una forma di sezione trasversale.
A proposito di Momento d'inerzia, Centroidi e altre Proprietà della Sezione
Abbiamo anche raccolto ulteriori informazioni per calcolare il momento di inerzia delle sezioni. Questa guida completa dovrebbe aiutare a fornire una base di conoscenza completa per tutto quello che è relativo al momento d'inerzia, centroidi, modulo di sezione e altre importanti proprietà della sezione geometrica. Nei segmenti seguenti, includiamo quello che è il momento d'inerzia, come calcolare il centroide, il momento d'inerzia e le comuni equazioni MOI con l'aiuto del Calcolatore del momento di inerzia e centroide SkyCiv.
Cos’è il Momento d’inerzia?
Il Momento d'Inerzia (più tecnicamente conosciuto come il momento d'inerzia dell'area, o il secondo momento dell'area) è un'importante proprietà geometrica utilizzata nell'ingegneria strutturale. È direttamente correlato alla quantità di resistenza materiale della sezione.
In generale, maggiore è il momento di inerzia, maggiore è la forza della sezione, e di conseguenza minore sarà la deviazione sotto carico. Il Momento d'Inerzia di un rettangolo, o qualsiasi forma per quella materia, è tecnicamente una misura di quanta coppia di torsione è necessaria per accelerare la massa su un asse - da qui la parola inerzia presente nel suo nome.
Come Trovare il Momento di Inerzia - Rettangolare
Per calcolare il momento di inerzia di un rettangolo, è possibile utilizzare la formula:
I = (b * h^3) / 12
I è il momento di inerzia del rettangolo
b è la larghezza del rettangolo
h è l'altezza del rettangolo
È importante notare che l'unità di misura per b e h deve essere coerente (ad esempio, pollici, millimetri, ecc.). Inoltre l'unità del risultato finale dipende dall'unità di input, per esempio se l'input è nel tester allora l'unità di risultato sarebbe m^4.
Esempio di calcolo del Momento d'inerzia
Diciamo che abbiamo un rettangolo con le seguenti dimensioni:
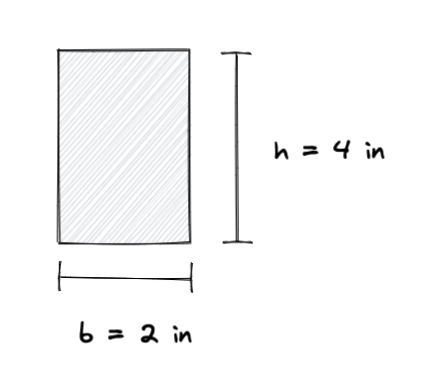
Utilizzando la formula per il momento di inerzia, possiamo calcolare il momento di inerzia del rettangolo come segue:
I = (b * h^3) / 12
I = (2 * 4^ 3) / 12
I = (2 * 64) / 12
= 10.67 in 4 pollici
Quindi vale il momento d'inerzia del rettangolo 10.67 4 pollici. Questo momento di inerzia riguarda l'asse centroidale, ricorda che se devi trovare il momento di inerzia su un asse diverso, dovrai usare una formula diversa o eseguire una trasformazione. È inoltre possibile verificare che l'unità sia sempre il prodotto della potenza dell'unità di input, in questo caso tutte le unità di input sono pollici, quindi il risultato è in pollici.
Possiamo verificare questo risultato con la calcolatrice di cui sopra, che mostra lo stesso risultato di 10.6667 in 4 pollici:
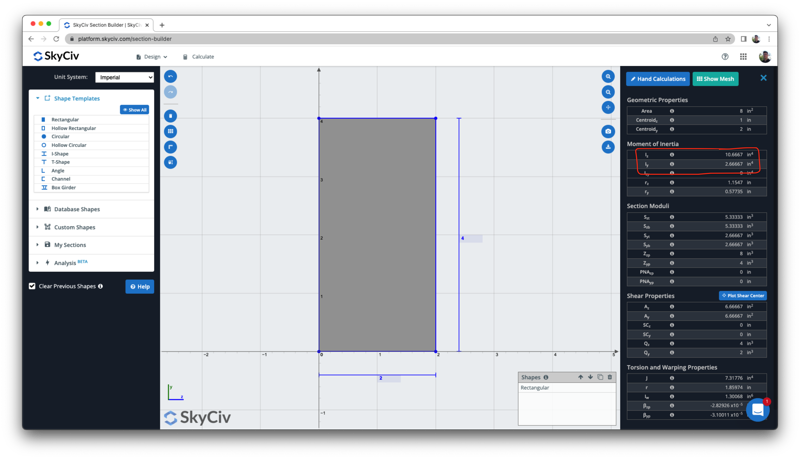
Come Trovare il Momento di Inerzia - I Beam
Ora diamo un'occhiata a un caso più complesso in cui la sezione trasversale è una trave a I, con diverse dimensioni della flangia. Il concetto è lo stesso, tuttavia l'approccio in questo caso è molto diverso. Fondamentalmente, dobbiamo considerare la trave a I come una combinazione di diversi rettangoli e sommare le diverse parti per ottenere le sezioni del Momento di Inerzia. In breve, dobbiamo seguire questi tre passi:
- Calcola l'asse neutro per l'intera sezione
- Calcolare il MOI di ogni parte
- Calcola il momento d'inerzia usando il Teorema dell'Asse Parallelo - che è essenzialmente la somma del momento d'inerzia individuale
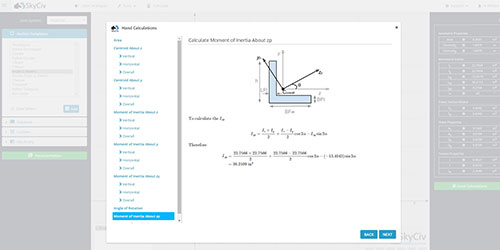
Consideriamo le seguenti sezioni:
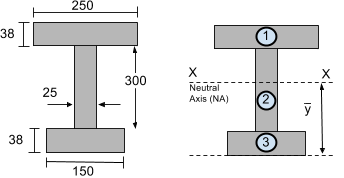
L'asse neutro (NA) si trova al centroide. Si tratta essenzialmente di una media ponderata dell'area e della distanza dal basso per ciascun segmento. Dobbiamo semplicemente usare l'equazione del centroide per calcolare il centroide verticale (y) di una forma a più segmenti.

Prenderemo il dato o la linea di riferimento dalla parte inferiore della sezione della trave. Ora troviamo Ai e yi per ogni segmento della sezione della trave a I mostrata sopra in modo che il centroide verticale o y possa essere trovato.


Ora abbiamo il centroide. Possiamo continuare a calcolare il momento d'inerzia. Per calcolare il momento di inerzia totale della sezione dobbiamo usare "teorema parallelo dell'asse" come definito qui:

Poiché l'abbiamo diviso in tre parti rettangolari, dobbiamo calcolare il momento di inerzia di ciascuna di queste sezioni. Ora possiamo usare la formula del momento d'inerzia rettangolare semplificata:
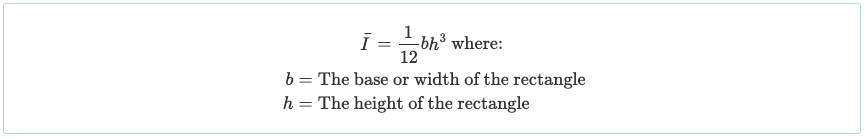
Ora abbiamo tutte le informazioni necessarie per usare il "teorema parallelo dell'asse" e trovare il momento totale di inerzia della sezione della trave a I. Nel nostro esempio del momento di inerzia:

Ancora una volta, possiamo confrontare questo risultato con quello del calcolatore di inerzia del momento libero per confrontare i risultati sia del centroide che del momento di inerzia, dove sia il centroide (216.29 pollici) che il momento di inerzia (4.74 x 10^8 in^ 4) corrispondono:
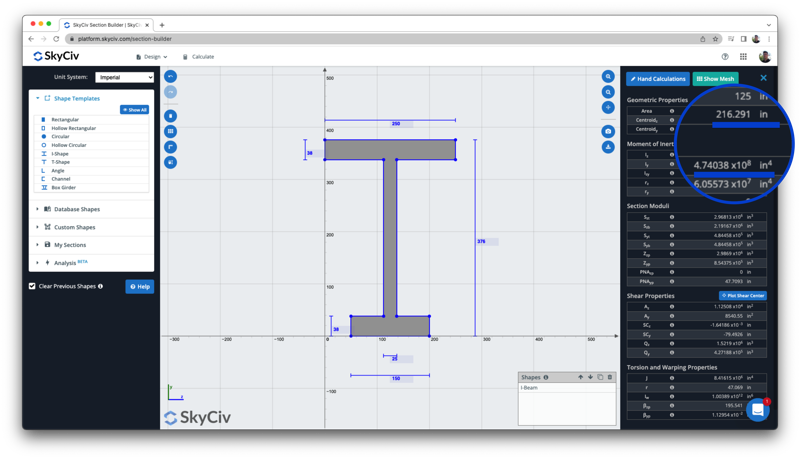
Equazioni del Momento d'inerzia
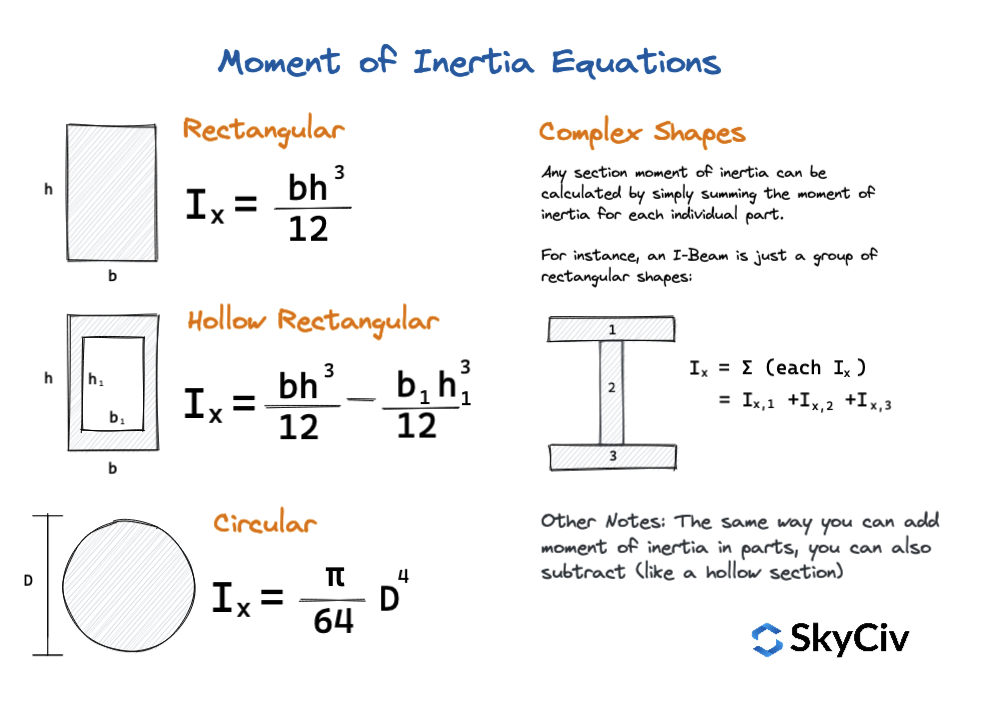
Le equazioni semplici possono anche essere usate per calcolare il momento di inerzia delle forme e delle sezioni comuni. Si tratta di rapide equazioni del momento d'inerzia che forniscono valori rapidi e sono un ottimo modo per confrontare o ricontrollare i risultati. Concentrandosi solo sulle forme semplici, il diagramma seguente mostra alcune di queste equazioni:
Calcolatore del Centroide SkyCiv
Un centroide, noto anche come 'centro geometrico', è il centro di massa di un oggetto con densità uniforme. Una dimostrazione semplificata di un centroide, sarebbe la posizione in cui si dovrebbe mettere una matita in equilibrio sul dito. La posizione in cui la matita è equilibrata e non cade, sarebbe la posizione approssimativa del centroide della matita. Considera la massa e la densità del materiale per determinare il punto in cui la massa della matita è uguale su entrambi i lati del dito, e quindi rappresenta il 'centro di massa' della matita.
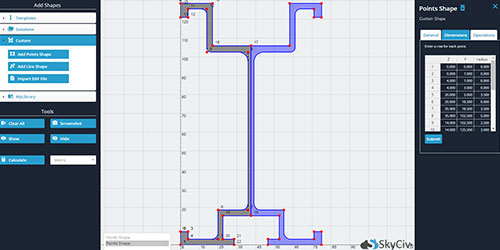
Il calcolatore del Centroide SkyCiv utilizza FEA per fornire risultati estremamente accurati in pochi secondi, indipendentemente dalla complessità della forma. Nella versione premium, gli utenti possono inserire le coordinate dei punti che definiscono la forma e la nostra calcolatrice vi darà le coordinate del centroide. Ciò include la possibilità di progettare forme personalizzate tramite importazione DXF, forme multiple (built-up) e forme punto personalizzate.
Oltre alla sua velocità e precisione, il nostro calcolatore è anche incredibilmente facile da usare. Con una semplice interfaccia utente, è possibile inserire le dimensioni della sezione e ricevere i valori delle proprietà della sezione (compreso il centroide della sezione della trave) in pochi secondi. Che tu stia lavorando a un progetto di design, sperimentando diverse sezioni o studiando per un esame, il calcolatore del Centroide SkyCiv è lo strumento perfetto per aiutarti a portare a termine il lavoro.
Calcolatore del Modulo di sezione
Come notato in precedenza, questo strumento gratuito fornisce anche un calcolo del modulo di sezione elastica, tuttavia, se stai iniziando come ingegnere potresti non capire quale sia. In poche parole, il modulo di sezione è una proprietà di una sezione trasversale che misura la resistenza alla flessione e calcolata come rapporto tra il momento di inerzia e la distanza dall'asse neutro alla fibra più distante. Il modulo di sezione elastica è rappresentato in questa equazione come:
Dove,
- S è il modulo di sezione
- I è il momento di inerzia della sezione sull'asse neutro
- y è la distanza dall'asse neutro al punto più distante della sezione
Ci sono due tipi di modulo di sezione: Elastico e Plastica. In America, S è tipicamente usato per riferirsi al modulo di sezione elastica mentre Z è usato per riferirsi al modulo di sezione plastica. In Gran Bretagna e Australia, questi sono tipicamente invertiti. Il modulo di sezione elastica è tipicamente indicato con una lettera Z, mentre il modulo di sezione plastica è indicato con una lettera S.
In generale, il modulo di sezione elastica viene utilizzato per la progettazione della sezione perché è applicabile fino al punto di snervamento per la maggior parte dei metalli. I metalli non sono tipicamente progettati per andare oltre il punto di snervamento del materiale.
Documentazione aggiuntiva
Si prega di fare riferimento alle seguenti pagine di documentazione per informazioni più dettagliate sul momento d'inerzia, su come calcolarlo per varie forme, e su come utilizzare il nostro calcolatore di centroidi:
Altri strumenti gratuiti disponibili
SkyCiv offre anche altri strumenti come lo strumento I size size e un software di progettazione strutturale gratuito. Il riquadro della sezione dinamica ti mostrerà anche una rappresentazione grafica della sezione del raggio. Quindi se vuoi calcolare il momento d'inerzia del cerchio, momento d'inerzia di un rettangolo o di qualsiasi altra forma, sentiti libero di usare il software in basso o il nostro builder di sezioni SkyCiv all-inclusive.
SkyCiv offre un'ampia gamma di software di analisi strutturale e progettazione cloud per ingegneri. Come azienda tecnologica in continua evoluzione, ci impegniamo a innovare e a sfidare i flussi di lavoro esistenti per risparmiare tempo agli ingegneri nei loro processi di lavoro e nei loro progetti.
Hai bisogno di più funzionalità ?
Passa al piano professionale per sbloccare le funzionalità complete