Progetto monopalo secondo ACI 318 (2014)
I pali sono elementi lunghi e sottili che trasferiscono i carichi dalla sovrastruttura al terreno più profondo o su una roccia con capacità portante adeguata. I materiali utilizzati per le pile possono includere il legno, acciaio, e concreto. L'installazione del palo nel terreno può essere guidata, forato, o jacked che vengono poi collegati ai cappucci dei pali. Molti fattori, come le condizioni del sito, tipo di terreno, la trasmissione dei carichi, sono considerati per classificare il tipo e l'installazione di pali. Questo articolo si concentrerà sulla progettazione di un palo di cemento in conformità con l'American Concrete Institute (ACI) 318 – 2014.
Il modulo SkyCiv Foundation Design include la progettazione di pali conformi all'American Concrete Institute (ACI 318) e standard australiani (AS 2159 & 3600).
Vuoi provare il software Foundation Design di SkyCiv? Il nostro strumento gratuito consente agli utenti di eseguire calcoli di carico senza alcun download o installazione!
Capacità di carico di un palo
Generalmente, i carichi verticali applicati sui pali sono sostenuti dall'appoggio del palo, e la resistenza all'attrito della pelle sviluppata lungo la sua lunghezza. La massima capacità di carico (QU) deve essere rappresentato dall'equazione (1). Viene applicato un fattore di sicurezza per calcolare la capacità di carico ammissibile (QA).
\({Q}_{u} = {Q}_{p} + {Q}_{S}\) (1)
QU = Capacità di carico massima
QP = Resistenza all'estremità
QS = Resistenza all'attrito della pelle
\({Q}_{A} = frac{{Q}_{U}}{FOS} \) (2)
QA = Capacità di carico ammissibile
FOS = Fattore di sicurezza
Per una guida più dettagliata, dai un'occhiata al nostro articolo sul calcolo la resistenza all'attrito della pelle e la capacità portante.
Resistenza strutturale di un singolo palo
Anche i pali sono soggetti a forze assiali, forza di taglio, e momento flettente, ecco perché sono strutturalmente progettati in modo simile alle colonne. Sezione 10.5.1.1 afferma che tutto il carico calcolato non deve superare le sue corrispondenti resistenze di progetto.
\( {operazione}_{N} ≤ {P}_{U} \) (3un carico)
\( {dolorante}_{N} ≤ {M}_{U} \) (3b)
\( {øV}_{N} ≤ {V }_{U} \) (3c)
PU, MU, V U = Fattore assiale, momento flettente, carichi di taglio
PN, MN, V N = Nominale assiale, momento flettente, carichi di taglio
ø = Fattori di riduzione della resistenza (tavolo 1)
| Fattori di riduzione della forza(ϕ) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Assiale | 0.65-0.90 | ||||||||||||
| Flessionale | 0.65-0.90 | ||||||||||||
| cesoia | 0.75 | ||||||||||||
tavolo 1: Fattori di riduzione della forza (tavolo 21.2.1, ACI 318-14)
Capacità di taglio di un singolo palo (øVN)
La resistenza a taglio nominale deve essere equivalente ai contributi combinati delle capacità di taglio del calcestruzzo e dell'armatura in acciaio.
Resistenza al taglio del calcestruzzo (V c)
Il contributo del calcestruzzo alla capacità di taglio viene calcolato come mostrato nell'equazione (4) che è definito nella sezione 22.5.5.1 of ACI 318-14.
\( {V }_{c} = 0.17 × λ × sqrt{fc'} × b × d \) (4)
λ = Fattore di modifica del calcestruzzo = 1 (Calcestruzzo di peso normale, tavolo 19.2.4.2)
fc’ = Resistenza del calcestruzzo
b = larghezza o diametro del pelo
d = 0.80 × profondità del mucchio (Sezione 22.5.2.2)
Resistenza al taglio delle barre d'acciaio (V S)
Il contributo dell'armatura a taglio laterale alla capacità di taglio è calcolato come il minimo tra le equazioni (5) e (6).
\( {V }_{S} = 0.066 × sqrt{fc'} × b × d \) (5)
\( {V }_{S} = frac{{A}_{v} × {f}_{sì} × d }{S} \) (6)
AV = Area delle barre d'armatura a taglio
fsì = Resistenza allo snervamento delle barre d'armatura a taglio
s = Interasse delle barre d'armatura a taglio
Resistenza a taglio nominale (øVN)
Riassumendo l'output dell'equazione 4-6 deve risultare alla resistenza a taglio nominale del palo. Fattore di riduzione della forza (ø) deve essere uguale a 0.75 come definito nella tabella 22.2.1 of ACI 318-14.
\( {øV}_{N} = ø × ({V }_{c} + {V }_{S}) ≤ {øV}_{U} \) (7)
Capacità assiali e flessionali di un unico palo (operazioneN, doloranteN )
Le capacità assiali e flessionali vengono verificate mediante un diagramma di interazione. Questo diagramma è una rappresentazione visiva del comportamento delle capacità flettenti e assiali causate da un aumento del carico dal puro punto flettente fino al raggiungimento di un punto di equilibrio.
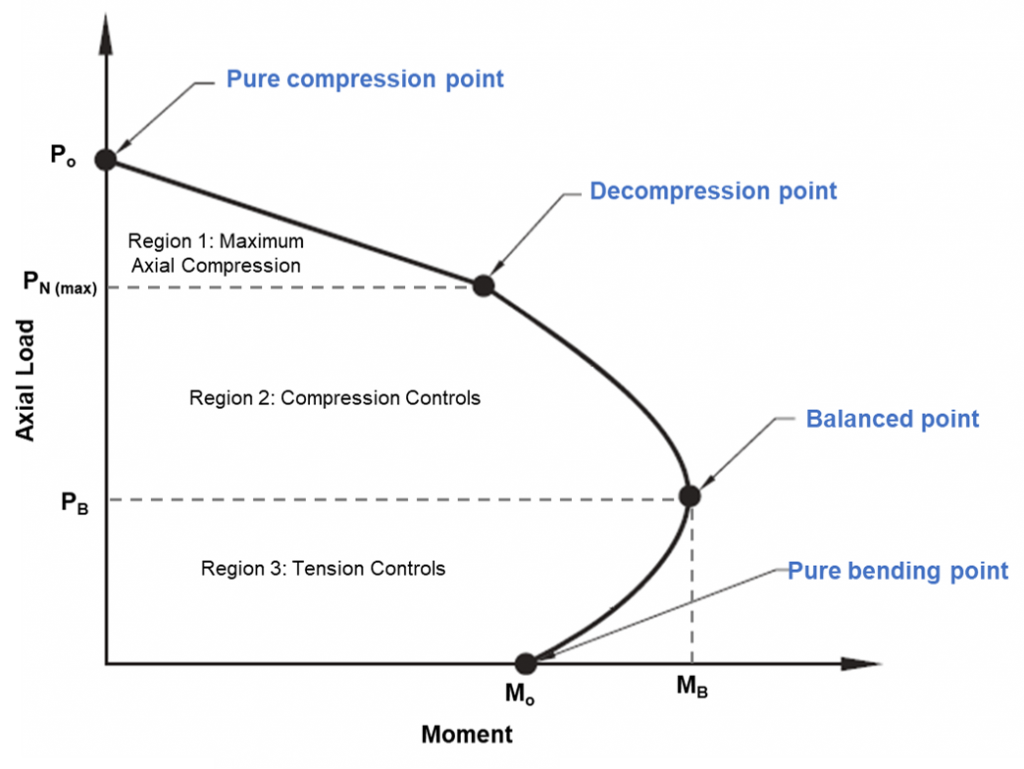
figura 1: Diagramma di interazione delle colonne
Diagramma di interazione delle colonne
Il punto di compressione pura sul diagramma è dove la pila fallirà la compressione puramente. A questo punto, il carico assiale viene applicato al baricentro plastico della sezione per rimanere in compressione senza piegarsi. La resistenza del palo tra il punto di compressione pura fino ai punti di decompressione può essere calcolata mediante interpolazione lineare. Il punto di decompressione è dove la deformazione del calcestruzzo alla fibra di compressione estrema è uguale a 0.003, e la deformazione nella fibra a trazione estrema è zero. Il punto di flessione puro è dove la capacità di carico assiale è zero. Tra il passaggio dal punto di decompressione al punto di flessione puro, si raggiunge una condizione equilibrata. A questo punto, la deformazione del calcestruzzo è al suo limite (ec=0,003), e la deformazione esterna dell'acciaio raggiunge la resa (eS=0,0025). Qualsiasi combinazione di carico assiale e momento flettente al di fuori del diagramma causerà un guasto.
Massima resistenza alla compressione assiale nominale per il progetto (operazioneN)
La resistenza assiale di progetto di una sezione deve essere limitata solo a 80-85% della resistenza assiale nominale per tenere conto dell'eccentricità accidentale.
\( {operazione}_{N} = ø × {P}_{Il} \) (8un carico)
\( {P}_{Il} = F × [0.85 × {f}_{c} × ({A}_{g} – {A}_{sto}) + ({f}_{y} × {A}_{sto}) ] \) (8b)
F = 0.80 (Cravatte)
F = 0.85 (Spirale)
Asol = Area lorda della sezione del palo
Asto = Area totale delle barre d'acciaio longitudinali
fy = Resistenza allo snervamento delle barre d'acciaio
Resistenza alla flessione nominale (doloranteN)
La costruzione del diagramma di interazione per la colonna comporta il tracciamento di una serie di valori di PN e MN. Valori per PN deve essere equivalente alla somma delle forze di trazione e compressione, come mostrato nelle Figure 2a e 2b, mentre il corrispondente MN si calcola risolvendo queste forze attorno all'asse neutro. Queste forze includono la forza di compressione che agisce sull'area di compressione e le forze esercitate da ciascuna delle barre d'armatura che possono essere di compressione o trazione. Di seguito viene suggerita una procedura generale per costruire un diagramma di interazione utilizzando le equazioni presentate.
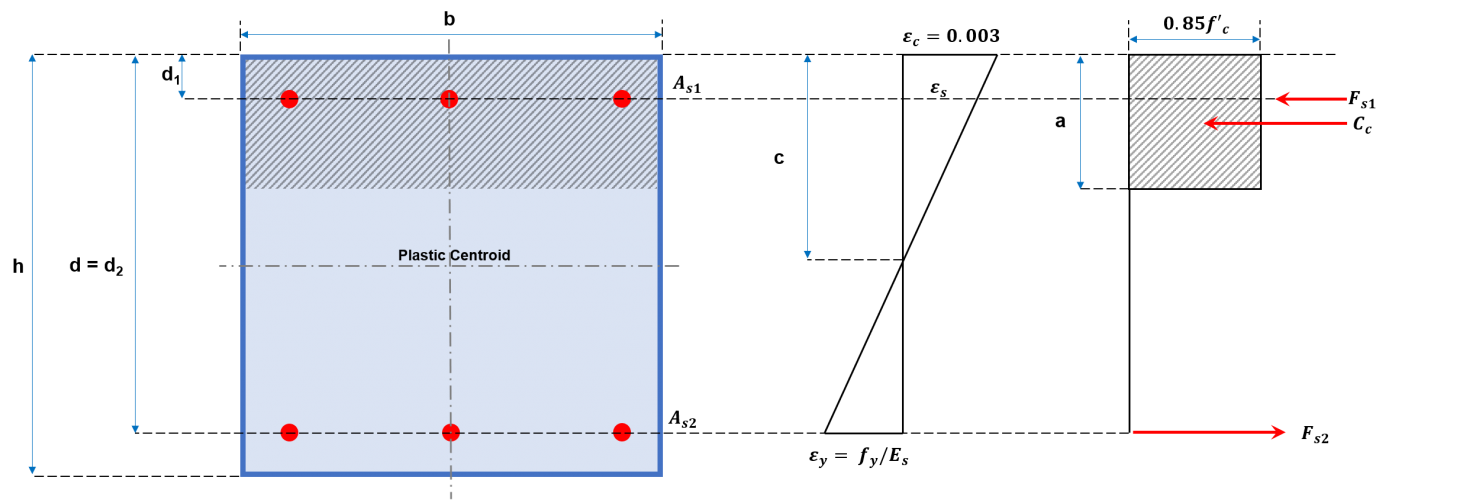
Figura 2a: Sezione rettangolare della colonna
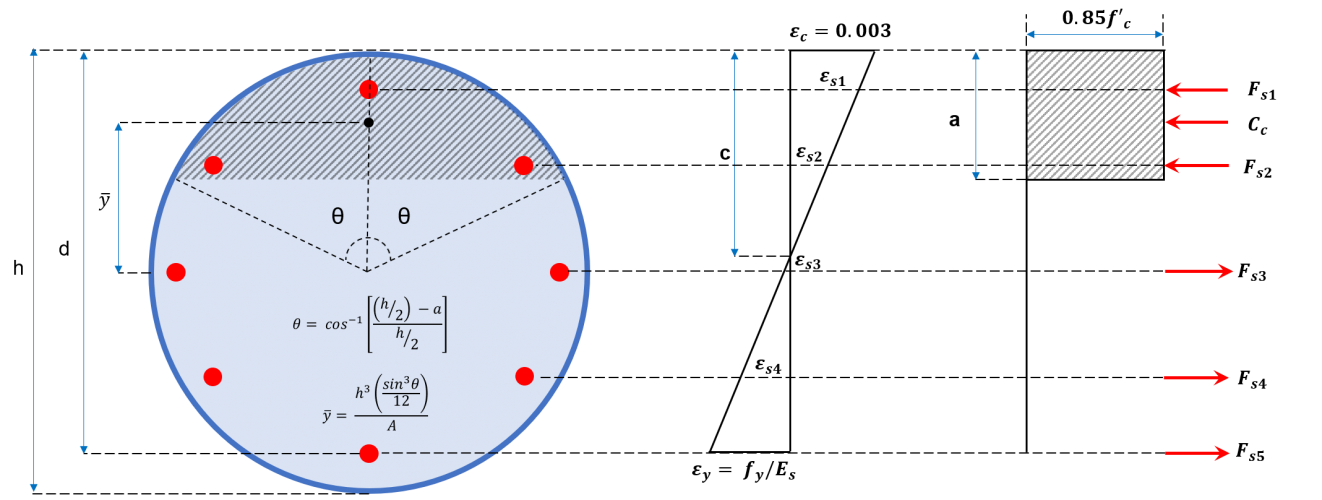
Figura 2b: Sezione di colonna circolare
Procedura generale per il diagramma di interazione di una colonna
(1) Calcola per il valore di PIl e PN (equazioni 8a e 8b).
(2) Determinare c e le deformazioni nei rinforzi.
\( c = 0.003 × frac{{d}_{1}}{0.003 + (Z + {e}_{y})} \) (9)
c = Profondità asse neutro
ey = Deformazione dell'acciaio = fy/ES
Z = Valore arbitrario (0, -0.5, -1.0, -2.5)
Occorre considerare una serie di casi selezionando varie posizioni dell'asse neutro, c. Per impostare le posizioni dell'asse neutro, le diverse deformazioni dell'acciaio devono essere selezionate moltiplicando un valore arbitrario Z per la resistenza allo snervamento dell'acciaio. Esiste un'ampia gamma di valori per Z. Tuttavia, ci sono solo quattro punti obbligatori da utilizzare per il diagramma di interazione.
- Z = 0: a questo punto, la deformazione allo strato estremo in tensione è zero. Questo punto segna il passaggio dalla giunzione a sovrapposizione di compressione consentita su tutte le barre longitudinali a una giunzione a sovrapposizione di tensione.
- Z = -0.5: questa distribuzione della deformazione influisce sulla lunghezza della giunzione a sovrapposizione di tensione in una colonna & è di solito tracciato su un diagramma di interazione.
- Z = -1: questo segna il punto di una condizione equilibrata. Questa distribuzione delle deformazioni segna il passaggio da cedimenti per compressione originati dallo schiacciamento della superficie di compressione della sezione a cedimenti per trazione iniziati dallo snervamento del rinforzo longitudinale.
- Z = -2.5: questo punto corrisponde al limite di deformazione controllato in tensione di 0.005.
(3) Calcolare le sollecitazioni negli strati di rinforzo.
\({f}_{e} ={e}_{e} × {E}_{S} \) (10)
fe = Stress in acciaio
ee = Deformazione in acciaio
\({e}_{e} = frac{c -{d}_{io}}{c} × 0.003 \) (11)
ES = Modulo di elasticità dell'acciaio
(4) Determinare l'altezza del blocco di sollecitazione di compressione, un carico.
\(a = {b}_{1} × c \) (a ≤ h)(12)
Per f'c ≤ 4000 psi (28 MPa):
b1 = 0.85
Per f'c > 4000 psi (28 MPa):
\( {b}_{1} = 0.85 – \frac{0.05 × (f'c – 4000)}{1000} \) (Imperiale)
\( {b}_{1} = 0.85 – \frac{0.05 ×(f'c – 28)}{7} \) (metrico)
(5) Calcolare le forze nel calcestruzzo e nell'acciaio.
Area del blocco di sollecitazione di compressione:
\({A}_{c} = a × b \) (Sezione rettangolare)
\({A}_{c} ={h}^{2} × frac{θ – sinθ cosθ}{4} \) (Sezione circolare)
Forza di compressione nel calcestruzzo:
\({C}_{c} = (0.85 × f'c) × {A}_{c}\) (14)
Forza di trazione in acciaio (dioa):
\({F}_{e} = {f}_{e} × {A}_{e} \) (15)
Forza di compressione in acciaio (dio > un carico):
\({F}_{e} = [{f}_{e} – (0.85 × f'c)] × {A}_{e} \) (16)
(6) Calcola per la capacità assiale (PN).
\({P}_{N} = {C}_{c} + Σ {F}_{e} \) (17)
(7) Calcola per la capacità di flessione (MN).
\({M}_{N} = [{C}_{c} × (\frac{h}{2} – \frac{un carico}{2})]+ Σ [{F}_{e} × (\frac{h}{2} – {d}_{io}) \) (18)
(8) Calcolare il valore del fattore di riduzione della forza (ø).
Come mostrato nella tabella 1, il fattore di riduzione della resistenza sia per assiale che per flessione varia da 0.60 per 0.90. Sezione 21.2 of ACI 318-14 dimostra il suo valore per il momento, forza assiale, o momento combinato e forza assiale, come mostrato nella tabella 2 sotto.
| Classificazione | Spirale | legato |
|---|---|---|
| Compressione controllata | 0.75 | 0.65 |
| Passaggio dalla compressione alla tensione | 0.75 + [50 × (et – 0.003) ] | 0.65 + [(250/3) × (et – 0.003) ] |
| Tensione controllata | 0.90 | 0.90 |
tavolo 2: Fattori di riduzione della forza per assiale, momento o combinare assiale e momento (tavolo 21.2.2, ACI 318-14)
(9) Ripeti i passaggi 2-8 con vari valori per Z.
(10) Tracciare nel diagramma i valori di øPN e øMN.
Progettazione di pali di cemento con SkyCiv Free Foundation Calculator
SkyCiv Calcolatore di fondazione gratuito ti aiuta con la progettazione di pali di cemento e altre attività come la progettazione di basi e pali di cemento. Dai un'occhiata ora per scoprire come il nostro calcolatore può aiutarti con il tuo progetto di pali di cemento!
Riferimenti
-
- Requisiti del codice di costruzione per calcestruzzo strutturale (2014). AC! 318-14 American Concrete Institute.
- Hsiao, JK. (2012). Effetti dell'asse di flessione sul momento di carico (P-M) Diagrammi di interazione per pilastri circolari in calcestruzzo che utilizzano un numero limitato di barre d'armatura longitudinali. Giornale elettronico di ingegneria strutturale 12 (1). Estratto da http from://www.ejse.org


