Βασικές αρχές της ροπής αδράνειας
Η ροπή αδράνειας μπορεί να εξαχθεί ως λήψη του στιγμή αδράνειας των εξαρτημάτων και εφαρμόζοντας τον τύπο μεταφοράς: I = εγώ0 + Ενα δ2. Έχουμε ένα ολοκληρωμένο άρθρο που εξηγεί την προσέγγιση επίλυση της ροπής αδράνειας.
Βασικά, η στιγμή της αδράνειας είναι η δεύτερη στιγμή της περιοχής, που μπορεί να εκφραστεί ως εξής:
[μαθηματικά] ΕΓΩ_{Χ}= int int y ^{2}δίνει [μαθηματικά] [μαθηματικά] ΕΓΩ_{και}= int int x ^{2}δίνει [μαθηματικά]
Για να παρατηρήσετε την παραγωγή των παρακάτω τύπων, προσπαθούμε να βρούμε τη στιγμή της αδράνειας ενός αντικειμένου, όπως ένα ορθογώνιο γύρω από τον κύριο άξονά του, χρησιμοποιώντας μόνο τον παραπάνω τύπο. Για να πάρετε τη στιγμή της αδράνειας, Τα όρια πρέπει να καθοριστούν έτσι ώστε να λαμβάνονται από τον άξονα περιστροφής στην ακραία ίνα του. Αυτό θα ήταν τα όρια του εξωτερικού ακέραιου. Το εσωτερικό ακέραιο έχει ένα όριο από 0 στο β. Εχοντας πεί αυτό, μπορούμε επίσης να εκφράσουμε το dA ως xdy, που θα γίνει bdy. Καθώς ο άξονας περιστροφής βρίσκεται στον ουδέτερο άξονα, Η ροπή αδράνειας μπορεί να ενσωματωθεί με ένα ανώτερο όριο h / 2 και ένα χαμηλότερο όριο 0 και πολλαπλασιάστηκε δύο φορές λόγω της συμμετρίας του ορθογωνίου. Αυτό μας αφήνει με το ακέραιο παρακάτω.
[μαθηματικά] ΕΓΩ_{Χ}= 2 int_{0}^{\frac{η}{2}} και ^{2}φίλε [μαθηματικά] Ολοκλήρωση, [μαθηματικά] ΕΓΩ_{Χ}= 2b αριστερά [ \frac{και ^{3}}{3} \σωστά ]_{0}^{\frac{η}{2}} [μαθηματικά] [μαθηματικά] ΕΓΩ_{Χ}= 2b αριστερά [ \frac{h ^{3}}{24}-0 \σωστά ] [μαθηματικά] [μαθηματικά] ΕΓΩ_{Χ}= frac{bh ^{3}}{12} [μαθηματικά]
Τύπος Ροπής Αδράνειας για Διατομές Δοκών
Το SkyCiv έχει συντάξει μια περίληψη των εξισώσεων ροπής αδράνειας για διατομές δέσμης (δεύτερη στιγμή της περιοχής). Η στιγμή των εξισώσεων αδράνειας είναι εξαιρετικά χρήσιμη για γρήγορους και ακριβείς υπολογισμούς. Οι τύποι συνοψίστηκαν στις απλούστερες φόρμες τους για την εξυπηρέτησή σας.
Το SkyCiv προσφέρει επίσης ένα Υπολογιστής δωρεάν ροπής αδράνειας για γρήγορους υπολογισμούς ή για να ελέγξετε ότι έχετε εφαρμόσει σωστά τον τύπο. Η στιγμή της αδράνειας τύπος για ορθογώνιο, κύκλος, έχουν δοθεί κοίλες και τριγωνικές δοκοί. Μερικά σημαντικά πράγματα που πρέπει να θυμάστε σχετικά με τη ροπή αδράνειας του εμβαδού μιας δέσμης είναι:
- Η ροπή αδράνειας της περιοχής είναι διαφορετική από τη στιγμή της αδράνειας
- Είναι επίσης γνωστή ως η δεύτερη στιγμή της περιοχής
- Είναι ένας σημαντικός παράγοντας εκτροπής (όσο μεγαλύτερο είναι το IΧ, η χαμηλότερη εκτροπή θα είναι)
- Οι μονάδες έχουν μήκος σε ισχύ 4
- Οι παρακάτω εξισώσεις δίνουν τη στιγμή της αδράνειας σε σχέση με το κέντρο του τμήματος
ΑΝΑΦΟΡΑ |
Εγώxx |
Εγώεε |
Στιγμή εξίσωσης αδράνειας για ορθογώνια ή ορθογώνια τμήματα |
||
|---|---|---|
 |
[μαθηματικά] \dfrac{bh ^ 3}{12} [μαθηματικά] | [μαθηματικά] \dfrac{β ^{3}η}{12} [μαθηματικά] |
Στιγμή εξίσωσης αδράνειας για κοίλο ορθογώνιο τμήμα |
||
 |
[μαθηματικά] \dfrac{bh ^ 3}{12} – \dfrac{b_1h_1 ^ 3}{12} [μαθηματικά] | [μαθηματικά] \dfrac{β ^ 3 ω}{12} – \dfrac{b_1 ^ 3h_1}{12} [μαθηματικά] |
Στιγμή εξίσωσης αδράνειας για κύκλο ή κυκλική ενότητα |
||
 |
[μαθηματικά] \dfrac{\πι}{64}Δ ^ 4 [μαθηματικά] | [μαθηματικά] \dfrac{\πι}{64}Δ ^ 4 [μαθηματικά] |
Στιγμή εξίσωσης αδράνειας για κοίλο κυκλικό τμήμα |
||
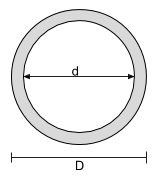 |
[μαθηματικά] \dfrac{\πι}{64}Δ ^ 4 – \dfrac{\πι}{64}δ ^ 4 [μαθηματικά] | [μαθηματικά] \dfrac{\πι}{64}Δ ^ 4 – \dfrac{\πι}{64}δ ^ 4 [μαθηματικά] |
Στιγμή εξίσωσης αδράνειας για ένα τρίγωνο Isosceles |
||
 |
[μαθηματικά] \dfrac{bh ^ 3}{36} [μαθηματικά] | [μαθηματικά] \dfrac{3β ^ 3 ω}{144} [μαθηματικά] |
Στιγμή εξίσωσης αδράνειας ενός τμήματος Ι |
||
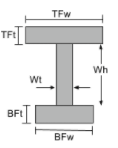 |
[μαθηματικά] \frac{TFw φορές TFt ^{3}}{12} +\frac{W φορές Wh ^{3}}{12} + \frac{BFw φορές BFt ^{3}}{12} +[μαθηματικά] [μαθηματικά] TFw φορές TFt φορές αριστερά ( BFt + Wh + frac{TFt}{2} -\μπαρ{και}_{bot} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] Wt φορές Wh φορές αριστερά ( BFt + frac{Τι}{2} -\μπαρ{και}_{bot} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] BFw φορές BFt φορές αριστερά ( \frac{Τι}{2} -\μπαρ{και}_{bot} \σωστά )^{2} [μαθηματικά] | [μαθηματικά] \frac{TFt φορές TFw ^{3}}{12} + \frac{Τι φορές Wt ^{3}}{12} + \frac{BFt φορές BFw ^{3}}{12} [μαθηματικά] |
Στιγμή εξίσωσης αδράνειας ενός τμήματος Τ |
||
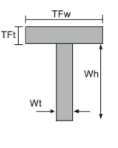 |
[μαθηματικά] \frac{TFw φορές TFt ^{3}}{12} + \frac{W φορές Wh ^{3}}{12} +[μαθηματικά] [μαθηματικά] TFw φορές TFt αριστερά ( Τι + \frac{TFt}{2} -\μπαρ{και}_{bot} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] Wt φορές Wh φορές αριστερά ( \frac{Τι}{2} – \μπαρ{και}_{bot} \σωστά )^{2} [μαθηματικά] | [μαθηματικά] \frac{TFt φορές TFw ^{3}}{12} + \frac{Τι φορές Wt ^{3}}{12} [μαθηματικά] |
Στιγμή εξίσωσης αδράνειας ενός τμήματος καναλιού |
||
 |
[μαθηματικά] \frac{TFw φορές TFt ^{3}}{12} + \frac{BFw φορές BFt ^{3}}{12} + \frac{W φορές h ^{3}}{12} +[μαθηματικά] [μαθηματικά] TFw φορές TFt φορές αριστερά ( η – \frac{TFt}{2} – \μπαρ{και}_{bot} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] BFw φορές BFt φορές αριστερά ( \frac{BFt}{2} – \μπαρ{και}_{bot} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] Wt φορές h φορές αριστερά ( \frac{η}{2} – \μπαρ{και}_{bot} \σωστά )^{2} [μαθηματικά] | [μαθηματικά] \frac{TFt φορές TFw ^{3}}{12} + \frac{BFt φορές BFw ^{3}}{12} + \frac{h φορές Wt ^{3}}{12} +[μαθηματικά] [μαθηματικά] TFt φορές TFw φορές αριστερά ( Β + \frac{TFw}{2} – \μπαρ{Χ}_{αριστερά} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] BFt φορές BFw φορές αριστερά ( Β + \frac{BFw}{2} – \μπαρ{Χ}_{αριστερά} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] h φορές Wt φορές αριστερά ( \frac{Β}{2} – \μπαρ{Χ}_{αριστερά} \σωστά )^{2} [μαθηματικά] |
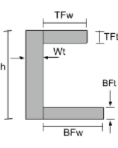
Στιγμή εξίσωσης αδράνειας των γωνιών |
||
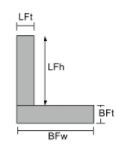 |
[μαθηματικά] \frac{BFw φορές BFt ^{3}}{12} + \frac{ LFt φορές LFh ^{3}}{12} +[μαθηματικά] [μαθηματικά] BFw φορές BFt φορές αριστερά ( \frac{BFt}{2}-\μπαρ{και}_{bot} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] LFt φορές LFh φορές αριστερά ( BFt + \frac{LFh}{2}-\μπαρ{και}_{bot} \σωστά )^{2} [μαθηματικά] | [μαθηματικά] \frac{BFt φορές BFw ^{3}}{12} + \frac{ LFh φορές LFt ^{3}}{12} +[μαθηματικά] [μαθηματικά] BFt φορές BFw φορές αριστερά ( \frac{BFw}{2}-\μπαρ{Χ}_{αριστερά} \σωστά )^{2} +[μαθηματικά] [μαθηματικά] LFh φορές LFt φορές αριστερά ( \frac{LFt}{2}-\μπαρ{Χ}_{αριστερά} \σωστά )^{2} [μαθηματικά] |
Χρησιμοποιήστε το SkyCiv Section Builder για υπολογισμούς χεριών
Σε αυτό το άρθρο, σας οδηγήσαμε στη φόρμουλα της στιγμής αδράνειας. Για περισσότερες πληροφορίες σχετικά με αυτό το θέμα, επισκεφθείτε το σεμινάριο μας για Ροπή Αδράνειας Διατομής Δοκού.
Το ήξερες Οικοδόμος ενότητας SkyCiv εμφανίζει επίσης τους υπολογισμούς με το χέρι για τα παρακάτω σχήματα?
- Ορθογώνιος, Κοίλο ορθογώνιο
- Εγκύκλιος, Κοίλη εγκύκλιος
- I-Beam, T-Beam
- Γωνία (L-Beam), Κανάλι
- Τριγωνικά τμήματα
Ελπίζουμε να βρείτε τον παραπάνω πίνακα πολύτιμο για τον τρόπο υπολογισμού μιας στιγμής αδράνειας ενός κύκλου, τρίγωνο, και ορθογώνια ροπή αδράνειας μεταξύ άλλων σχημάτων. Έχουμε επίσης ένα χρήσιμο Υπολογιστής ροπής αδράνειας, ένα απλοποιημένο από Οικοδόμος ενότητας SkyCiv, που χειρίζεται αυτούς τους υπολογισμούς για εσάς ή εγγραφείτε σήμερα για να ξεκινήσετε με το λογισμικό SkyCiv!


