ΣΦΑΙΡΙΚΗ ΕΙΚΟΝΑ
ΟΠΩΣ ΚΑΙ 4100:2020 Steel Structures uses the limit state method for the design of structural steel members. This method involves calculating factored loads and reduced capacities to account for variability in loading conditions and material properties. For the ultimate limit state (ULS) design to be satisfied, the following relationship must be true:
\(ULS \;Factor * Load ≤ Reduction \;Factor * Capacity\)
This document outlines the procedure for designing a steel member in accordance with AS 4100 SkyCiv Renderer API SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα μονάδα μέτρησης.
Contents
Ιδιότητες υλικού
Fabrication
In Australia there are three typical forms of structural steel fabrication:
- Hot Rolled Sections: Steel billet (blocks) are heated, rolled through a mill into the desired shape, then cooled. Examples include Universal Beams/Columns, Παράλληλα κανάλια φλάντζας (PFC) and Angle sections.
- Cold Formed Sections: Steel billet is pressed at room temperature into the desired shape. Examples include Rectangular Hollow Sections (RHS) and Circular Hollow Sections (CHS).
- Fabricated Sections: Multiple hot rolled flat plates are welded together to form a steel section. Examples include Welded Beams/Columns.
Steel Grade
Australia has numerous steel grades (strengths) that can be used for design in accordance with AS 4100:2020. Grade availabilities for different section types are outlined below.
| Βαθμός | WB / WC | Μπορείτε να βρείτε μια σειρά τύπων σύνδεσης που ταιριάζουν στις ανάγκες σας χωρίς να αντιμετωπίζετε ακατάστατα συστήματα διεπαφής χρήστη που απαιτούν μια απότομη καμπύλη εκμάθησης για να ξεκινήσετε / Μπορείτε να βρείτε μια σειρά τύπων σύνδεσης που ταιριάζουν στις ανάγκες σας χωρίς να αντιμετωπίζετε ακατάστατα συστήματα διεπαφής χρήστη που απαιτούν μια απότομη καμπύλη εκμάθησης για να ξεκινήσετε | PFC | ΑΥΤΗ / UA | RHS / SHS | CHS |
|---|---|---|---|---|---|---|
| 250 | NO | NO | NO | NO | NO | ΝΑΙ |
| 300 | ΝΑΙ | ΝΑΙ | ΝΑΙ | ΝΑΙ | NO | NO |
| 350 | ΝΑΙ | ΝΑΙ | ΝΑΙ | ΝΑΙ | ΝΑΙ | ΝΑΙ |
| 400 | ΝΑΙ | NO | NO | NO | NO | NO |
| 450 | NO | NO | NO | NO | ΝΑΙ | NO |
Αντοχή διαρροής
The yield strength of a steel section is dependent on its Grade, with higher grades having higher yield stresses. The yield strength of Hot Rolled and Fabricated sections vary depending on the thickness of the section. Thicker steel sections typically have lower yield strengths than thinner sections of the same Grade.
Cold Formed Sections are the exception to this rule and have a consistent yield strength for each Steel Grade, regardless of section thickness. Section yield strength and ultimate (εντάσεως) strength values can be calculated using Table 2.1 in AS 4100:2020.
Selecting a Section in SkyCiv AS 4100 Σχεδιασμός μελών χάλυβα
ο SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα tool allows users to select a Standard section from the SkyCiv database or design a completely Custom section. When a Standard section is selected, flange and web yield strengths are automatically calculated based on the steel grade using AS 4100 Τραπέζι 2.1. When a Custom section is selected, the user must input values for flange and web yield strength. Standard sections can also be used with a Custom steel grade if specified by the user.
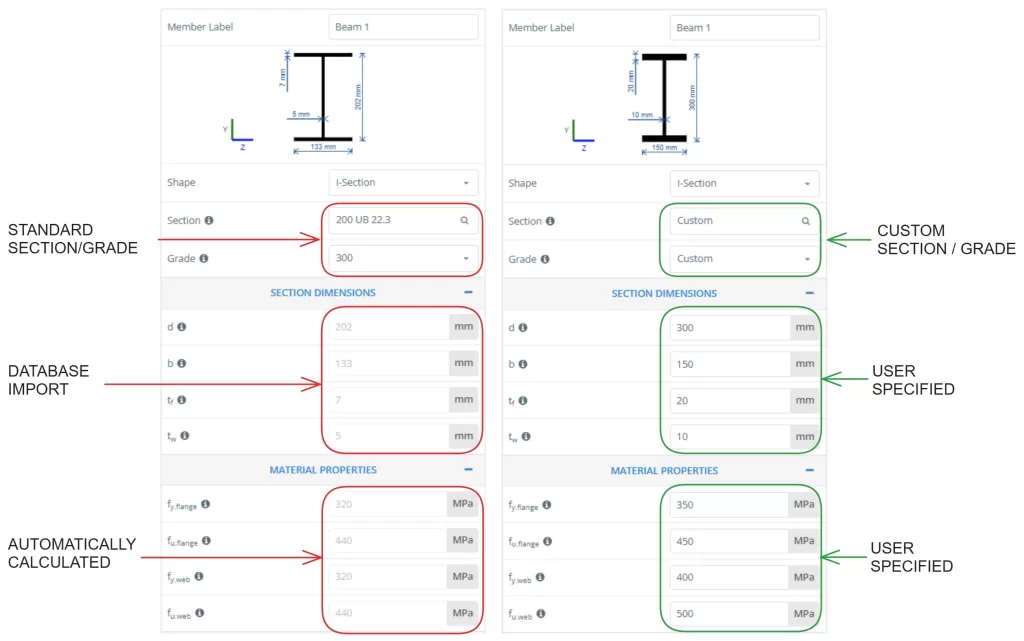
Section Capacity
Κάμψη
Section Bending Moment Capacity
ΟΠΩΣ ΚΑΙ 4100:2020 calculates the bending moment capacity of a steel section as follows:
\(M_s = f_y*Z_e\)
Where fκαι is the yield stress of the material, and Zμι is the effective section modulus. The section modulus of a shape is a geometric property which quantifies the bending resistance of a shape. In structural engineering we use two section modulus values, ο elastic (ΜΕ) και πλαστική ύλη (μικρό) συντελεστή ενότητας. Σημείωση, design standards in other regions sometimes interchange the symbols for elastic and plastic section modulus.
The elastic section modulus assumes the entire section (σχήμα) remains elastic under bending, δηλ. no part of the section exceeds the yield strength (φάκαι) of the material. This generally occurs when the extreme fibers in the section (top/btm) reach yielding. The elastic section modulus of a section is calculated as follows:
\(Z = \frac{Εγώ}{και}\)
Where I is the second moment of area and y is the geometric centroid of the shape.
The plastic section modulus assumes that the entire section reaches the yield strength of the material under bending, which means parts of the section will exceed the yield strength and experience plastic deformation. The plastic section modulus of a section is calculated as follows:
\(S = A_C*y_C + A_T*y_T \)
Where Aντο and AΤ are the areas on either side of the Plastic Neutral Axis (PNA), και γντο / καιτ are the distance from the PNA to the centroid of those areas. Σημείωση, the PNA location is equal to the geometric centroid location for symmetric shapes but will δεν equal the geometric centroid location for asymmetric shapes.
Section Classification
Some steel shapes may have elements of the shape locally buckle before reaching their yield strength, meaning the full capacity of the elastic/plastic section modulus cannot be achieved. This typically occurs in larger, thinner shapes, which are more susceptible to local buckling. ΟΠΩΣ ΚΑΙ 4100 uses the effective section modulus (Ze) value to account for the possibility of local buckling and reduce the bending capacity of the section accordingly. ΟΠΩΣ ΚΑΙ 4100 classifies sections into three categories:
- Compact: Compact sections are not susceptible to local buckling and can achieve their full plastic moment capacity, meaning the entire section can reach its yield strength under bending.
- Non-Compact: Non-compact sections can reach yield strength in the extreme fibres of the section (elastic moment capacity) but cannot achieve their plastic moment capacity before local buckling occurs.
- Slender: Slender sections cannot achieve their elastic moment capacity before local buckling occurs.
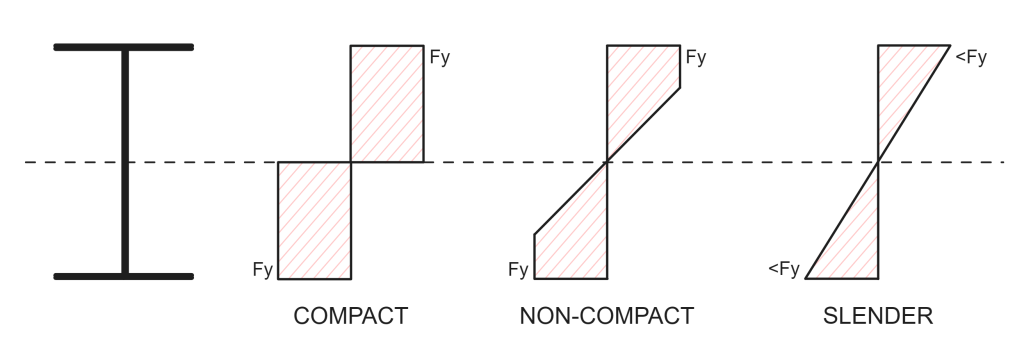
Section Slenderness
ΟΠΩΣ ΚΑΙ 4100 determines the section classification by calculating the slenderness of each element within a section and finding the “critical element” that will buckle in compression first. For an I-section, the elements are broken down as shown below. Slenderness values are only calculated for outstand elements, δηλ. elements which are not restrained in both directions. The area of connection between a flange and web (shown in white below) is restrained in both directions and hence is not susceptible to local buckling.
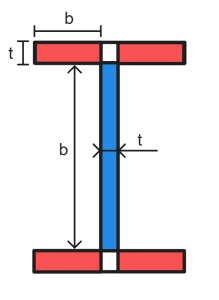
The slenderness of a flat element is calculated as follows:
\(λ_e = \frac{σι}{τ}\τ.μ.{\frac{f_y}{250}}\)
ΟΠΩΣ ΚΑΙ 4100 Τραπέζι 5.2 contains values for plasticity and yield slenderness limits (λep & λey) for compression plate elements based on stress distribution, edge support and residual stresses. The critical element of a section is the element with the highest λμι / λey αναλογία. The slenderness values of this element (λμι) are used to classify the entire section (referred to as λμικρό).
Αν λμικρό ≤ λsp the section is compact. For compact sections, the effective section modulus is calculated as follows:
\(Z_e = Z_c = min(μικρό,1.5*ΜΕ)\)
Where S is the plastic section modulus, and Z is the elastic section modulus of the section. The term Zντο is used interchangeably for the effective section modulus of a compact section.
Αν λsp ≤ λμικρό ≤ λτου the section is non-compact. For non-compact sections, the effective section modulus is calculated as follows:
\(Z_e = [(\frac{λ_{του} – λ_{μικρό}}{λ_{του} – λ_{sp}})(Z_c-Z)]\)
Where Zντο is the effective section modulus for a compact section.
Αν λμικρό > λτου the section is slender. For a slender section with flat plate elements in uniform compression, the effective section modulus is calculated as follows:
\(Z_e = Z(\frac{λ_{του}}{λ_s})\)
Σημείωση, the effective section modulus for circular hollow sections or flat plat elements with tension at the unsupported edge is calculated differently. Refer AS 4100 Ρήτρα 5.2.5 for further information.
Calculating Section Bending Capacity in SkyCiv AS 4100 Σχεδιασμός μελών χάλυβα
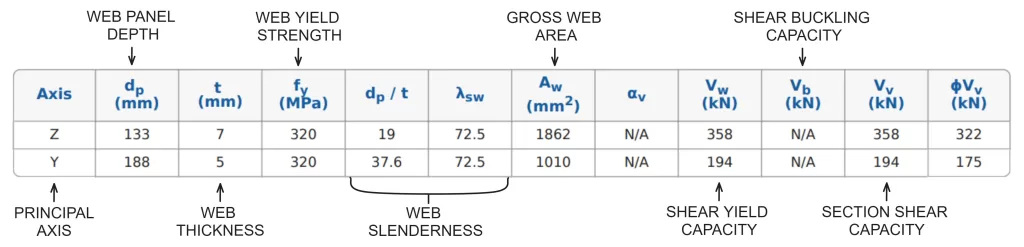
ο SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα tool calculates slenderness classifications and section bending capacities for positive and negative bending about both principal axes. The results of the slenderness classification check for a 230 PFC are detailed below.
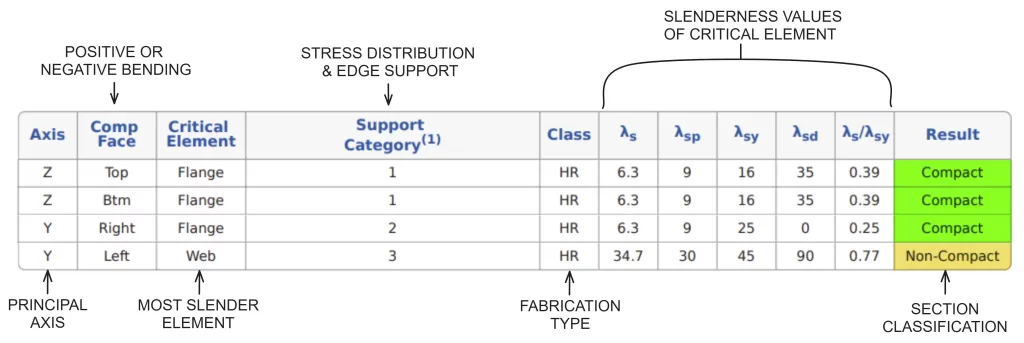
It’s apparent that the slenderness values and section classification are different depending on the direction of bending. This is because the stress distributions and edge support values change depending on which elements are in compression or tension, resulting in different slenderness limit values.
Once section slenderness is known, the module calculates the section bending moment capacity (Κυρία) about each principal axis for positive and negative bending. For symmetric shapes (such as I-Sections), this value will be the same in the positive and negative direction. Asymmetric shapes will have different section bending capacities in the positive and negative bending direction, such as the 230 PFC shown in the example below.

Κουρεύω
Section Shear Capacity
ΟΠΩΣ ΚΑΙ 4100 only considers the web of a section to contribute to its shear capacity. Hence the shear capacity of a section (Vv) is equal to the web shear capacity. Vertical stiffeners can be added to a section to increase its shear capacity if required. The capacity of an unstiffened web is calculated differently depending on whether the shear stress distribution across the web is uniform or non-uniform. The following shear stress distributions are assumed for standard section shapes:
| Σχήμα | Shear Stress Distribution |
|---|---|
| I-Section | Στολή |
| T-Section | Non-Uniform |
| Parallel Flange Channel (PFC) | Στολή |
| Rectangular Hollow Section (RHS) | Non-Uniform |
| Circular Hollow Section (CHS) | Στολή |
Uniform Shear Stress Distribution
The shear capacity of a section with uniform shear stress distribution (Βεσύ) is calculated differently depending on the slenderness of the web panel. For a non-slender web, capacity is calculated as follows:
\(\frac{d_p}{t_w} ≤ \frac{82}{\τ.μ.{\frac{f_y}{250}}}\rightarrow V_u = V_w = 0.6*f_y*A_w\)
For a Circular Hollow Section Vv = Vβ = 0.36*fκαι*ΕΝΑ (not impacted by section slenderness).
When the web of the section is slender capacity is calculated as follows:
\(\frac{d_p}{t_w} > \frac{82}{\τ.μ.{\frac{f_y}{250}}}\rightarrow V_u = V_b = α_v*V_w\)
\(α_v = \left[\frac{82}{(\frac{d_p}{t_w})\τ.μ.{\frac{f_y}{250}}}\σωστά]^2\)
Where dΠ is the clear depth of the web panel (δηλ. depth excluding flanges), τβ is the thickness of the web panel, φάκαι is the web yield strength and Aβ is the gross sectional area of the web. Note Aβ is calculated differently for welded and hot rolled sections. For hot rolled sections, ΕΝΑβ takes the web depth as the entire section depth (ρε). For welded sections, ΕΝΑβ only takes the clear web depth between the flanges (ρεΠ). Rectangular Hollow Sections also use dΠ for calculation of Aβ.
Non-Uniform Shear Stress Distribution
The shear capacity of a section with uniform shear stress distribution (Ββ) is calculated as follows:
\(V_v = \frac{2*V_u}{0.9+\αριστερά(\frac{f*_{vm}}{f*_{va}}\σωστά)} ≤ V_u\)
Where Vεσύ is the section shear capacity with a uniform shear stress distribution and f*vm /f*va is the ratio of maximum and average design shear stresses in the web.
Calculating Shear Capacity in SkyCiv AS 4100 Σχεδιασμός μελών χάλυβα
ο SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα tool calculates the shear capacity of a section in both principal axes. Minor axis (ΜΕ) shear capacity is calculated using the contribution of the section flanges, excluding any contribution from the section web. Results from the shear capacity calculations for a 200 Μπορείτε να βρείτε μια σειρά τύπων σύνδεσης που ταιριάζουν στις ανάγκες σας χωρίς να αντιμετωπίζετε ακατάστατα συστήματα διεπαφής χρήστη που απαιτούν μια απότομη καμπύλη εκμάθησης για να ξεκινήσετε 22.3 are detailed below.
Συμπίεση
Section Compression Capacity
ΟΠΩΣ ΚΑΙ 4100 calculates the compression capacity (Νμικρό) of a concentrically loaded section as follows:
\(N_s = k_f*A_n*f_y\)
Where kφά is the form factor of the section, ΕΝΑν is the net area of the cross section (gross area excluding penetrations/holes) and fκαι is the yield strength of the section. The form factor of a section represents how much of a section can contribute to its compression capacity before local buckling occurs. The form factor is calculated as follows:
\(k_f = \frac{A_e}{A_g}\)
Where Aσολ is the gross area of the section, and Aμι είναι το “effective area” του τμήματος, δηλ. the gross area of the section minus any “ineffective” areas under compression. An ineffective area is part of the section that will buckle before it reaches its yield capacity under compression. Effective areas are calculated by finding the “αποτελεσματικό πλάτος” of each flat plate element within a section and recalculating the section area using these adjusted width values. The effective width of a flat plate element is calculated as follows:
\(b_e = b\left(\frac{λ_{ey}}{λ_{μι}}\σωστά) ≤ b\)
Οπου:
\(λ_e = \frac{σι}{τ}\τ.μ.{\frac{f_y}{250}}\)
Σημείωση, most design software (συμπεριλαμβανομένου SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα) uses the section yield strength for element slenderness calculations, rather than the specific yield strength of the web/flange. This will always provide a conservative result. The b values used for λμι calculation are identical to the dimensions used for bending section slenderness checks (with the flange split about the web), but the b used for bμι calculation is the total flange/web width. λey is taken from AS 4100 Τραπέζι 6.2.4, depending on the edge support and residual stresses of that element.
The effective width of a circular hollow section is calculated as follows:
\(d_e = min(ρε_{ο}\τ.μ.{\αριστερά(\frac{λ_{ey}}{λ_{μι}}\σωστά)}, ρε_{ο}\αριστερά(\frac{3*λ_{ey}}{λ_{μι}}\σωστά)^ 2) ≤ d_{ο}\)
Οπου:
\(λ_e = \left(\frac{d_o}{τ}\σωστά)\αριστερά(\frac{f_y}{250}\σωστά)\)
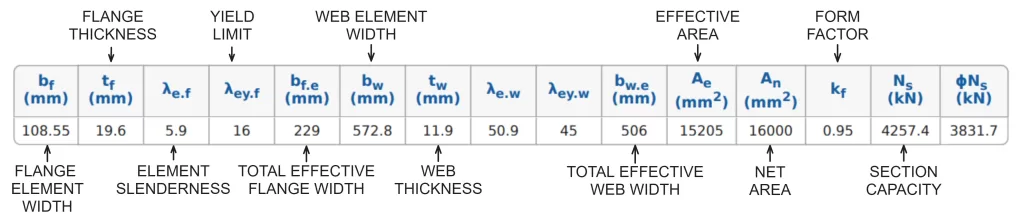
Calculating Section Compression Capacity in SkyCiv AS 4100 Σχεδιασμός μελών χάλυβα
ο SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα tool calculates the form factor and section compression capacity (Νμικρό) for standard Australian sections and custom user-defined sections. Results from the section compression capacity calculations for a 610UB 125 are detailed below.
Ενταση
Section Tension Capacity
ΟΠΩΣ ΚΑΙ 4100 calculates the capacity of a tension member (Nt) ως εξής:
\(N_t = min(ΕΝΑ_{σολ}*φά_{και}\; ,\; 0.85*k_t*A_n*f_u)\)
Where Aσολ is the gross area of the section, ΕΝΑν is the net area of the cross section (gross area excluding penetrations/holes), φάκαι is the yield strength of the section, φάεσύ is the tensile (ultimate) strength of the section and kτ is the tensile force distribution correction factor. The kτ used in design varies depending on the section shape and connection type. Connections which provide uniform force distribution result in a kτ factor of 1.0, connections with unequal force distribution result in a kτ factor between 0.75-1.0.
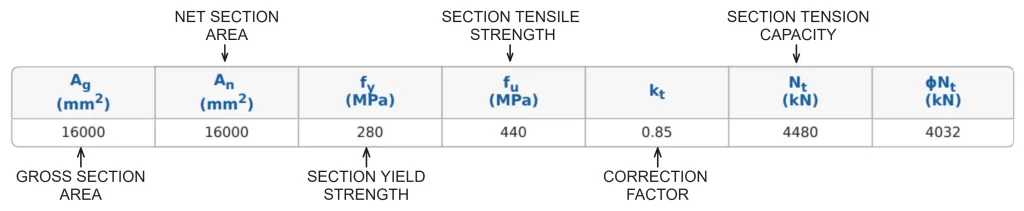
Calculating Tension Capacity in SkyCiv AS 4100 Σχεδιασμός μελών χάλυβα
ο SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα tool allows users to specify the section kτ value for used in design. A lower kτ value will result in a lower section tension capacity. Το SkyCiv AS 4100 Member Design calculator assumes no significant holes are present in the section, hence Aν is taken as equal to Aσολ. Results from the section tension capacity calculations for a 610UB 125 are detailed below.
Member Capacity
Κάμψη
Member Bending Moment Capacity
The bending moment capacity of a steel member may not always be governed by the bending moment capacity of the section (Μμικρό). This is because members can fail by another method before the capacity of the section is reached. Lateral torsional buckling is a common failure method for long/unrestrained steel members, which occurs when the section rotates away from its major axis (towards its minor axis) reducing its moment capacity in the direction of bending.
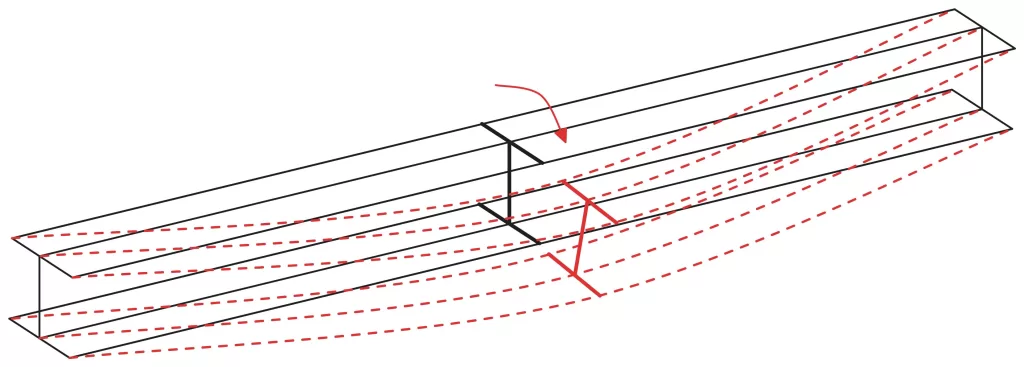
ΟΠΩΣ ΚΑΙ 4100 contains guidance on calculating nominal member capacity (Μσι), which factors the section capacity of a steel member (Μμικρό) to account for the impact of member slenderness and restraint conditions.
Members with Full Lateral Restraint
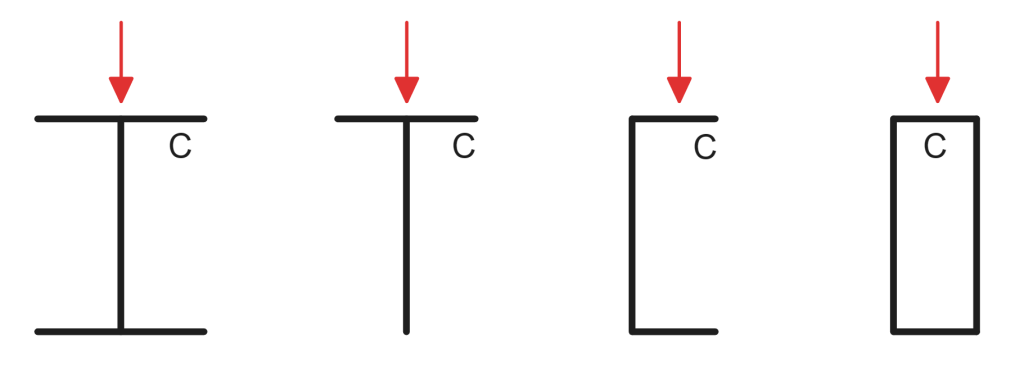
Critical Flange
The critical flange of a cross-section is the flange which would deflect the furthest during buckling, eventually resulting in lateral torsional buckling failure. This is typically the compression flange of a member. Critical flange locations for standard sections under vertical loading are shown below.
Full Lateral Restraint
Shorter members with high rotational/lateral rigidity are less likely to rotate out of plane under loading, reducing the likelihood of lateral torsional buckling failure. If a member is short/rigid enough it will be able to reach its section moment capacity (Μμικρό) before another failure method occurs. Members which satisfy this condition are deemed as having “Full Lateral Restraint”.
\(Γεμάτος \; Πλευρικός \; θα εκτελέσει τον τύπο σύμφωνα με το AISI S100-12 \; \rightarrow M_b = M_s\)
ΟΠΩΣ ΚΑΙ 4100 Ρήτρα 5.3.2 provides guidance on calculating the Full Lateral Restraint limit for a member. Κυκλικές κοίλες τομές (CHS) and Square Hollow Sections (SHS) are not susceptible to lateral torsional buckling, as they have high lateral/torsional rigidity and equal section moment capacities about both axes. Hence these sections are generally assumed to achieve Full Lateral Restraint regardless of member length.
Continuous Lateral Restraint
Members which have continuous restraint to the critical flange along their entire length are deemed as having “Continuous Lateral Restraint”. Continuous Lateral Restraint is considered equivalent to Full Lateral Restraint for the calculation of member bending capacity (Μσι).
Members without Full Lateral Restraint
The bending moment capacity of a member that doesn’t achieve full lateral restraint is calculated as follows:
\(M_b = α_m*α_s*M_s ≤ M_s\)
Where αΜ is the moment modification factor and αμικρό is the slenderness reduction factor. ΟΠΩΣ ΚΑΙ 4100 Ρήτρα 5.6 outlines the procedure for calculating αΜ and αμικρό.
Minor Axis Member Bending Capacity
The bending capacity for a member bent about its minor axis (Μσι) is equal to the minor axis section capacity (Μμικρό) about that axis. The minor axis section capacity reflects is the minimum capacity that section can achieve about any axis, hence the member cannot rotate from this axis into a less-favourable orientation.
Calculating Member Bending Capacity in SkyCiv AS 4100 Σχεδιασμός μελών χάλυβα
ο SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα tool calculates carries out full lateral restraint checks and calculates member bending moment capacities about both principal axes for positive and negative bending. Users also have the option of selecting “Continuous Lateral Restraint” to bypass the Full Lateral Restraint check. Results from the member bending capacity calculations for a 3m long 200UB22.3 are detailed below.
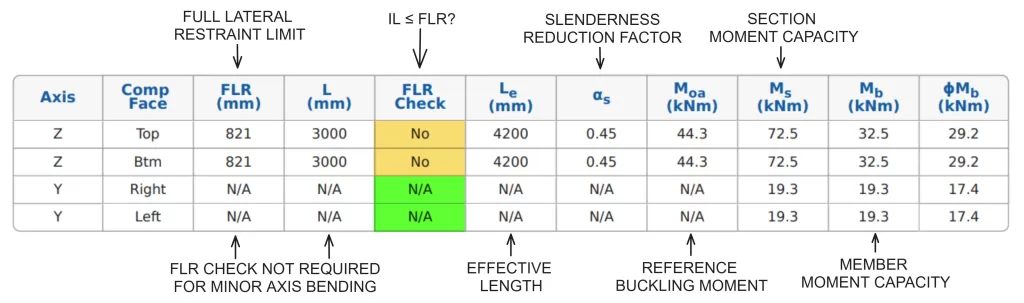
Σημείωση, this calculator assumes αΜ = 1.0 and βμικρό = -1.0 in all calculations. Cantilevered members are not supported by this tool.
Συμπίεση
Member Compression Capacity
The axial compression capacity of a member is also affected by its length, lateral rigidity and restraint conditions. Unrestrained, longer members are likely to fail due to flexural buckling before the section (squash) capacity is reached. ΟΠΩΣ ΚΑΙ 4100 contains guidance on calculating nominal member capacity (Νντο), which factors the compression section capacity (Νμικρό) to account for the impact of member slenderness and restraint conditions.
\(N_c = α_c*N_s ≤ N_s\)
Where αντο is the member slenderness reduction factor. Ρήτρα 6.3.3 K= Συντελεστής οφέλους δοκιμής 4100 provides guidance on calculating αντο. Member compression capacity must be checked about both axes to find the governing value.
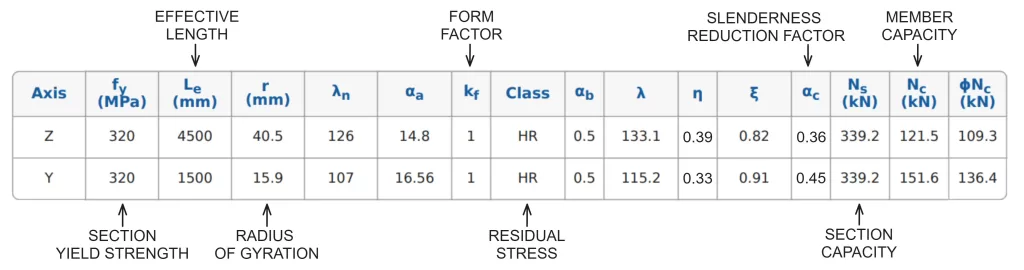
Calculating Member Compression Capacity in SkyCiv AS 4100 Σχεδιασμός μελών χάλυβα
ο SkyCiv AS 4100:2020 Σχεδιασμός μελών χάλυβα tool calculates member compression capacity about both principal axes based on restraint lengths and effective length factors specified by the user. Results from the member compression capacity calculations for a 200UB22.3 with an unrestrained length of 4500mm and 1500mm in the Z and Y axis (αντίστοιχα) are detailed below.
Λογισμικό δομικού σχεδιασμού SkyCiv
SkyCiv offers a wide range of Structural Analysis and Engineering Design Software, συμπεριλαμβανομένου:
- AS / NZS 1664 Σχεδιασμός αλουμινίου
- AS / NZS 4600 Σχεδιασμός τεγίδων
- ΟΠΩΣ ΚΑΙ 3600 Σχεδιασμός διατμητικού τοίχου από σκυρόδεμα
- ΟΠΩΣ ΚΑΙ 2870 Οικιστική πλάκα σε σχέδιο βαθμού
- AS / NZS 1576 Σχεδιασμός σκαλωσιάς
- ΟΠΩΣ ΚΑΙ 4055 Υπολογιστής φορτίου ανέμου
Δομικός μηχανικός
BEng (Εμφύλιος), DipEng (Λογισμικό)


