Η θεμελίωση είναι ένα ουσιαστικό στοιχείο μιας κατασκευής για την παροχή συνολικής σταθερότητας με τη μετάδοση και την κατανομή των συνολικών φορτίων της κατασκευής στο έδαφος. Ρηχά θεμέλια, όπως ορθογώνιο ή τετράγωνο απομονωμένο πέλμα, είναι ο προτιμώμενος τύπος θεμελίωσης λόγω της απλότητας κατασκευής τους και του συνολικού κόστους τους σε σύγκριση με τις βαθιές θεμελιώσεις. Η εκτίμηση της πίεσης βάσης επηρεάζει δραματικά τη σχεδίαση και το μέγεθος του πέλματος. Τυπικά, η αναλογία χρησιμότητας μεταξύ της επιτρεπόμενης φέρουσας ικανότητας του εδάφους και της κυρίαρχης βασικής πίεσης κάτω από το πέλμα είναι η βάση του αρχικού μεγέθους του πέλματος. Μόλις καθοριστούν οι αρχικές διαστάσεις του πέλματος, περαιτέρω έλεγχοι σχεδιασμού για ασφάλεια και σταθερότητα, όπως μονόδρομη και αμφίδρομη διάτμηση, ικανότητα κάμψης, και έλεγχοι μήκους ανάπτυξης, ελέγχονται ανάλογα με τον κώδικα σχεδιασμού που χρησιμοποιείται.
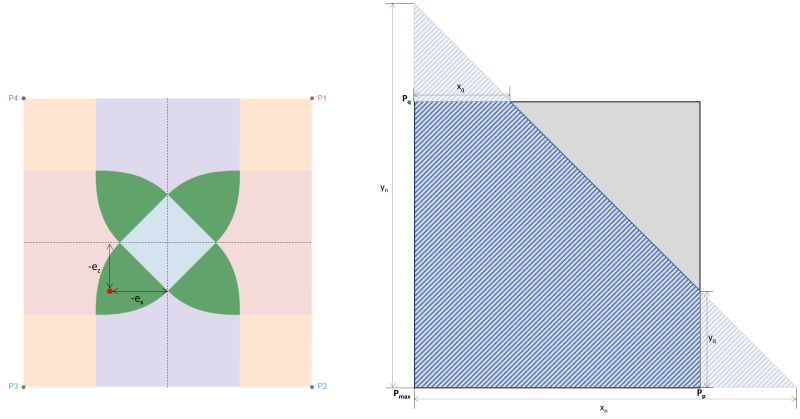
Όταν ένα πέλμα υποβάλλεται σε διαξονική κάμψη (ΜΧ, Μμε), υποτίθεται ότι το αξονικό φορτίο (Π) δρα σε μια συντεταγμένη εκκεντρικότητας (μιΧ, μιμε) όπου υπάρχει τάση περιστροφής από το κέντρο. Η αλληλεπίδραση μεταξύ εδάφους και βάσης εξαρτάται κυρίως από τη διάσταση του πέλματος και την προκύπτουσα εκκεντρότητα των εφαρμοζόμενων φορτίων. Ανάλογα με τη θέση της προκύπτουσας εκκεντρότητας, η πίεση βάσης προκαλεί την πλήρη ή μερική συμπίεση του πέλματος. Στην πράξη, Συνιστάται ο σχεδιασμός ενός πέλματος σε πλήρη συμπίεση. Η μερική συμπίεση ή η απώλεια επαφής μεταξύ του εδάφους και της βάσης δεν πρέπει να παραμεληθεί, αλλά οι περισσότεροι σχεδιαστές αποφεύγουν αυτό το σενάριο λόγω της πολυπλοκότητας του υπολογισμού του. Το πέλμα είναι σε πλήρη συμπίεση όταν η προκύπτουσα εκκεντρότητα βρίσκεται εντός του πυρήνα ή κάτω από τη ζώνη C. Η εκκεντρικότητα έξω από τη ζώνη C θέτει το πέλμα σε μερική συμπίεση. Φιγούρα 1 δείχνει τις διαφορετικές καθορισμένες ζώνες σε ορθογώνια βάση.
Αυτό το άρθρο θα επικεντρωθεί στον υπολογισμό των πιέσεων γωνιών κάτω από διαφορετικές ταξινομήσεις ζωνών με βάση το Bellos & Ιχνος (2017) και Σ.Σ. του Ray (1995) σπουδές.
Ταξινομήσεις ζωνών ορθογώνιας βάσης
Οι ταξινομήσεις ζωνών μιας ορθογώνιας βάσης προέρχονται από πολλαπλές μελέτες από διαφορετικούς συγγραφείς για την ανάπτυξη μιας πρακτικής προσέγγισης για την εκτίμηση της κατανομής της πίεσης του εδάφους υπό αναμενόμενες συνθήκες φόρτισης. Όπως φαίνεται στο σχήμα 1, υπάρχουν πέντε διαφορετικές περιοχές (Ζώνες Α-Ε) ανάλογα με τη θέση της προκύπτουσας εκκεντρότητας. Κάθε ζώνη αντιστοιχεί σε διαφορετική φόρτιση, κατανομή βασικής πίεσης, και παραμόρφωση. Ζώνη Γ, γνωστός και ως πυρήνας, είναι ο κύριος πυρήνας. Είναι η ιδανική περιοχή για να σχεδιάσετε μια βάση, με αποτέλεσμα την πλήρη συμπίεση στο πέλμα. Οι διαστάσεις αυτής της περιοχής είναι ισοδύναμες με 1/6 του αντίστοιχου μήκους του πέλματός του.
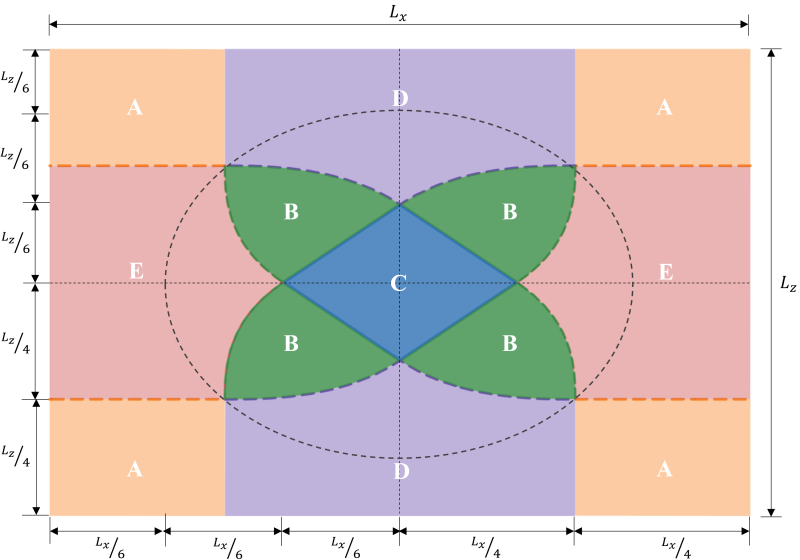
Φιγούρα 1: Ταξινομήσεις ζωνών ορθογώνιας βάσης
Ο δευτερεύων πυρήνας είναι η ελλειπτική περιοχή (που οριοθετείται από τη διακεκομμένη γραμμή στο σχήμα 1) με τους κύριους και δευτερεύοντες ημιάξονες του ίσους με 1/3 του αντίστοιχου μήκους του πέλματός του. Η περιοχή αυτή καλύπτει ολόκληρες τις ζώνες Β & Γ και ορισμένα τμήματα των ζωνών Δ & μι. Ο δευτερεύων πυρήνας οδηγεί σε μερική συμπίεση του πέλματος. Είναι καλή πρακτική η διατήρηση της εκκεντρότητας εντός της δευτερεύουσας ζώνης για ένα αποδεκτό σχέδιο βάσης.
Η εκκεντρικότητα πέρα από τη δευτερεύουσα ζώνη είναι το αποτέλεσμα υψηλής διαξονικής φόρτισης. Καλύπτει ολόκληρη τη ζώνη Α και τα υπόλοιπα τμήματα των ζωνών Δ & μι. Συνιστάται να αποφεύγεται ο σχεδιασμός της βάσης σε αυτές τις περιοχές καθώς υπάρχει κίνδυνος ανατροπής. Ως εκ τούτου, Συνιστάται να επανασχεδιαστούν οι διαστάσεις του πέλματος για αυτόν τον τύπο φόρτωσης.
Στη συνέχεια απαριθμούνται οι αναλυτικοί τύποι για την επίλυση των γωνιακών πιέσεων σε κάθε ταξινόμηση ζώνης.
Ζώνη Γ (Κύριος πυρήνας, Πλήρης ζώνη συμπίεσης)
Οπως αναφέρθηκε, αυτή είναι η πιο προτιμώμενη περίπτωση για το σχεδιασμό ποδιών, καθώς μπορεί να θέσει ολόκληρη τη βάση της βάσης σε συμπίεση, όπως φαίνεται στο σχήμα 2. Αυτή η περίπτωση αντιπροσωπεύεται από μικρή εκκεντρικότητα εντός του πυρήνα ή καθόλου εκκεντρικότητα. Φιγούρα 2 δείχνει την εκκεντρότητα εντός του πυρήνα με τη μέγιστη πίεσή του στις γωνίες P3 & P4 και ελάχιστη πίεση στις γωνίες P1 & Ρ2.
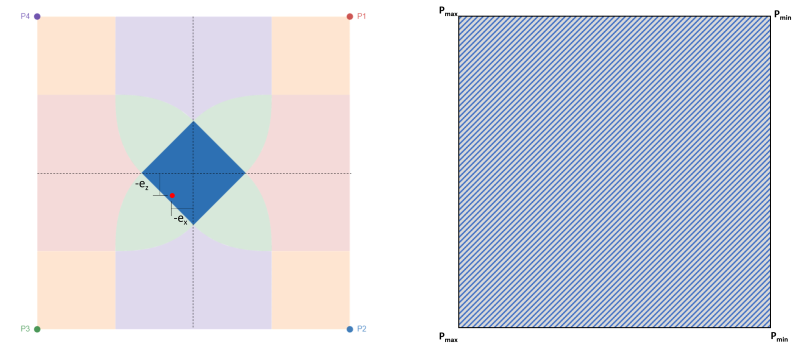
Φιγούρα 2: Εκκεντρικότητα (-μιΧ, -μιμε) στη Ζώνη Γ & περιοχή πλήρους συμπίεσης
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση & ελάχιστες γωνιακές πιέσεις (πανεμορφη & Ιχνος, 2017):
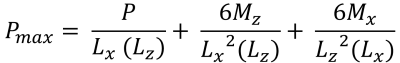
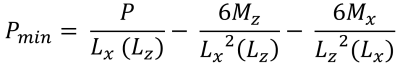
| Γωνιακές πιέσεις με βάση την εκκεντρικότητα | ||||
|---|---|---|---|---|
| Π1 | Π2 | Π3 | Π4 | |
| +μιΧ, +μιμε | ΠΜέγιστη | ΠΜέγιστη | Πελάχ | Πελάχ |
| +μιΧ, -μιμε | ΠΜέγιστη | ΠΜέγιστη | Πελάχ | Πελάχ |
| -μιΧ, -μιμε | Πελάχ | Πελάχ | ΠΜέγιστη | ΠΜέγιστη |
| -μιΧ, +μιμε | Πελάχ | Πελάχ | ΠΜέγιστη | ΠΜέγιστη |
Ζώνη Α (Τριγωνική ζώνη συμπίεσης)
Αυτή η θήκη αντιστοιχεί σε τέσσερις ορθογώνιες περιοχές σε κάθε γωνία του πέλματος. Εμφανίζεται συνήθως με μεγάλη διαξονική εκκεντρότητα, επιβάλλοντας μια υψηλή τριγωνική συμπιεστική περιοχή σε μια από τις γωνίες, όπως φαίνεται από τη σκιασμένη περιοχή στο σχήμα 3. Οι υπόλοιπες γωνίες χάνουν την επαφή με το έδαφος. Ως εκ τούτου, αυτή η περίπτωση δεν ενδείκνυται για σχεδιασμό.
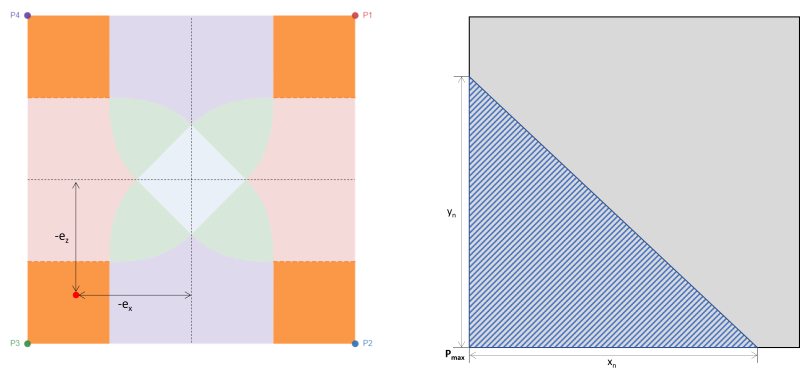Φιγούρα 3: Εκκεντρικότητα (-μιΧ, -μιμε) στη Ζώνη Α & τριγωνική περιοχή συμπίεσης γύρω από το P3
Μέγιστη πίεση (πανεμορφη & Ιχνος, 2017):
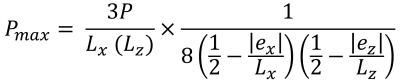
| Γωνιακές πιέσεις με βάση την εκκεντρικότητα | ||||
|---|---|---|---|---|
| Π1 | Π2 | Π3 | Π4 | |
| μιΧ(+), μιμε(+) | ΠΜέγιστη | 0 | 0 | 0 |
| μιΧ(+), μιμε(-) | 0 | ΠΜέγιστη | 0 | 0 |
| μιΧ(-), μιμε(-) | 0 | 0 | ΠΜέγιστη | 0 |
| μιΧ(-), μιμε(+) | 0 | 0 | 0 | ΠΜέγιστη |
Ζώνη Δ (Τραπεζοειδής ζώνη συμπίεσης)
Η ζώνη D αντιστοιχεί επίσης σε μεγάλες εκκεντρότητες στις περιοχές που συνδέονται με την κατεύθυνση x του πέλματος, όπως φαίνεται στο σχήμα 4. Η εκκεντρικότητα στην κατεύθυνση z (μιμε) είναι πολύ μεγαλύτερη από την κατεύθυνση x (μιΧ). Σε αυτήν την περίπτωση, δύο γωνίες του πέλματος χάνουν την επαφή με το έδαφος και δημιουργούν μια τραπεζοειδή συμπιεστική περιοχή. Σε σύγκριση με τη ζώνη Α, που βρίσκεται εξ ολοκλήρου εκτός της δευτερεύουσας ζώνης, ένα τμήμα της ζώνης Δ εξακολουθεί να καλύπτεται από τη δευτερεύουσα ζώνη.
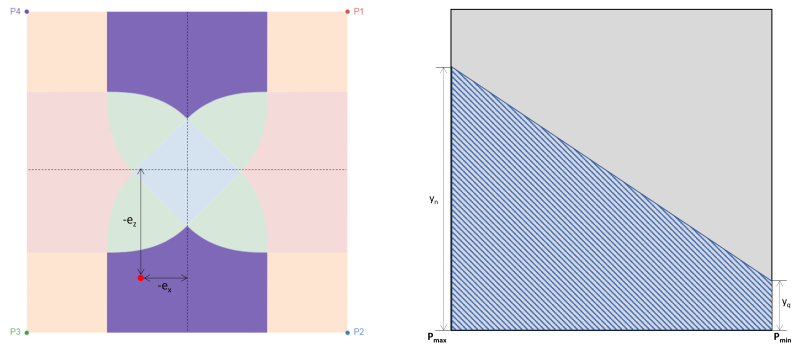
Φιγούρα 4: Εκκεντρικότητα (-μιΧ, -μιμε) στη Ζώνη Δ & τραπεζοειδής περιοχή συμπίεσης γύρω από το P3
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση & ελάχιστες γωνιακές πιέσεις (πανεμορφη & Ιχνος, 2017):
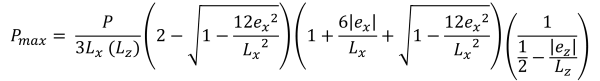
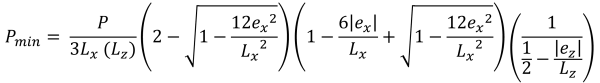
Κάθετα ύψη της τραπεζοειδούς θλιπτικής περιοχής (πανεμορφη & Ιχνος, 2017):
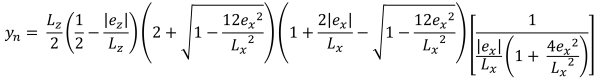
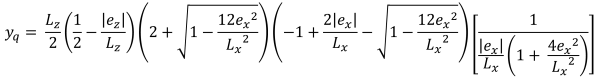
| Γωνιακές πιέσεις με βάση την εκκεντρικότητα | ||||
|---|---|---|---|---|
| Π1 | Π2 | Π3 | Π4 | |
| μιΧ(+), μιμε(+) | ΠΜέγιστη | 0 | 0 | Πελάχ |
| μιΧ(+), μιμε(-) | 0 | ΠΜέγιστη | Πελάχ | 0 |
| μιΧ(-), μιμε(-) | 0 | Πελάχ | ΠΜέγιστη | 0 |
| μιΧ(-), μιμε(+) | Πελάχ | 0 | 0 | ΠΜέγιστη |
Ζώνη Ε (Τραπεζοειδής ζώνη συμπίεσης)
Παρόμοια με τη ζώνη Δ, αυτή η περίπτωση παράγει επίσης μια τραπεζοειδή συμπιεστική περιοχή αλλά προκαλείται από μια μεγάλη εκκεντρότητα στην κατεύθυνση x(μιΧ).
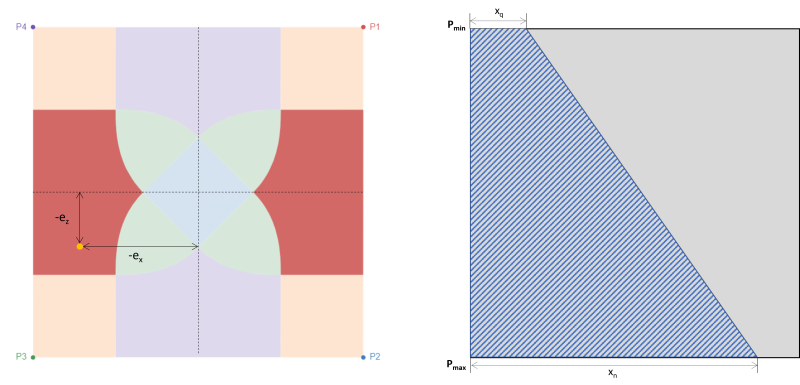Φιγούρα 5: Εκκεντρικότητα (-μιΧ, -μιμε) στη Ζώνη Ε & τραπεζοειδής περιοχή συμπίεσης γύρω από το P3
Η συμβολή του σκυροδέματος στη διατμητική ικανότητα υπολογίζεται όπως φαίνεται στην εξίσωση & ελάχιστες γωνιακές πιέσεις (πανεμορφη & Ιχνος, 2017):
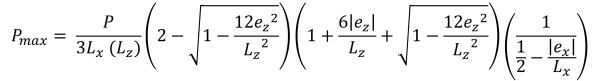
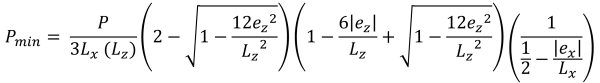
Οριζόντιες βάσεις της τραπεζοειδούς συμπιεστικής περιοχής (πανεμορφη & Ιχνος, 2017):
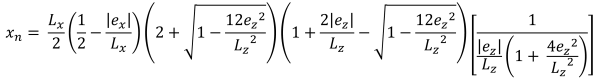
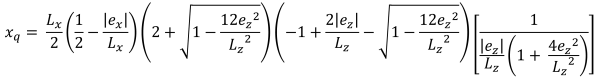
| Γωνιακές πιέσεις με βάση την εκκεντρικότητα | ||||
|---|---|---|---|---|
| Π1 | Π2 | Π3 | Π4 | |
| μιΧ(+), μιμε(+) | ΠΜέγιστη | Πελάχ | 0 | 0 |
| μιΧ(+), μιμε(-) | Πελάχ | ΠΜέγιστη | 0 | 0 |
| μιΧ(-), μιμε(-) | 0 | 0 | ΠΜέγιστη | Πελάχ |
| μιΧ(-), μιμε(+) | 0 | 0 | Πελάχ | ΠΜέγιστη |
Ζώνη Β (Πεντάγωνη ζώνη συμπίεσης)
Αυτή η περίπτωση συμβαίνει όταν τα ασκούμενα φορτία στα πόδια δημιουργούν μια μέτρια εκκεντρότητα εντός της δευτερεύουσας ζώνης. Οι περιοχές που καλύπτονται από τη ζώνη Β οριοθετούνται από δύο καμπύλες πλευρές και μια επίπεδη βάση γύρω από τις εξωτερικές πλευρές της ζώνης Γ. Σε αυτήν την περίπτωση, παράγεται μια πενταγωνική συμπιεστική περιοχή, και μόνο μια γωνία του πέλματος χάνει την επαφή με το έδαφος. Ωστόσο, Οι λύσεις που παρέχονται παρακάτω είναι ελαφρώς πολύπλοκες και απαιτούν αριθμητικές μεθόδους επίλυσης για τις γωνιακές πιέσεις και το x & y τομές της συμπιεστικής περιοχής.
Γωνιακές πιέσεις (πανεμορφη & Ιχνος, 2017):
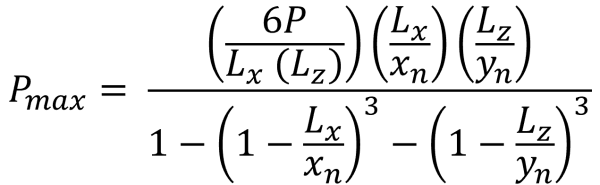
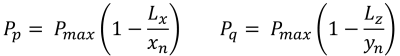
Πεντάγωνες πλευρές της συμπιεστικής περιοχής (πανεμορφη & Ιχνος, 2017):
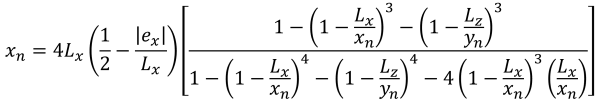
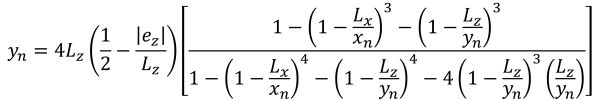
| Γωνιακές πιέσεις με βάση την εκκεντρικότητα | ||||
|---|---|---|---|---|
| Π1 | Π2 | Π3 | Π4 | |
| μιΧ(+), μιμε(+) | ΠΜέγιστη | Πε | 0 | ΠΠ |
| μιΧ(+), μιμε(-) | ΠΠ | ΠΜέγιστη | Πε | 0 |
| μιΧ(-), μιμε(-) | 0 | ΠΠ | ΠΜέγιστη | Πε |
| μιΧ(-), μιμε(+) | Πε | 0 | ΠΠ | ΠΜέγιστη |
Εναλλακτικά, μια πιο άμεση λύση από τον Σ.Σ. ακτίνα (1995) μπορεί να χρησιμοποιηθεί για τις γωνιακές πιέσεις και τομές της πενταγωνικής θλιπτικής ζώνης. Οι εξισώσεις δίνονται παρακάτω:
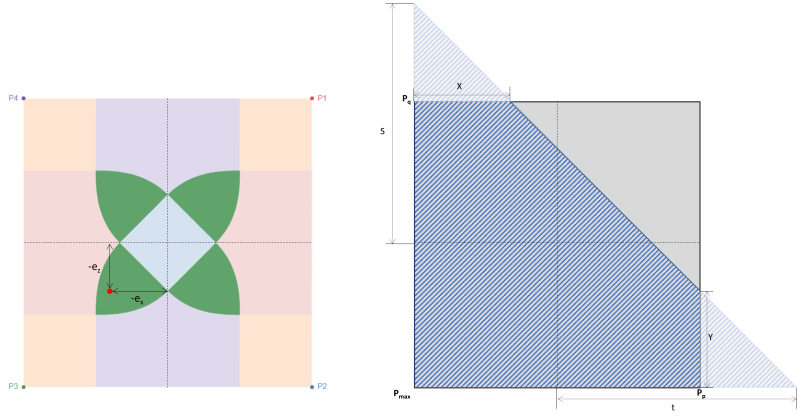
Γωνιακές πιέσεις (Σ.Σ. ακτίνα, 1995):
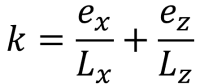
Πεντάγωνες πλευρές της συμπιεστικής περιοχής (Σ.Σ. ακτίνα, 1995):
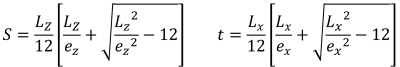
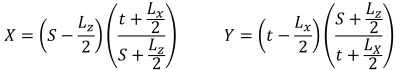
Το SkyCiv's Ενότητα σχεδίασης θεμελίων είναι ικανό να λύσει τις βασικές πιέσεις μιας ορθογώνιας βάσης από σκυρόδεμα. Πρόσθετοι έλεγχοι σχεδιασμού σύμφωνα με διαφορετικούς κώδικες σχεδιασμού (ACI 318-14, Αυστραλιανό πρότυπο 2009 & 2018, Ευρωκώδικας, και καναδικά πρότυπα) είναι επίσης διαθέσιμα.
ΤΕΛΕΥΤΑΙΑ ΑΝΑΒΑΘΜΙΣΗ
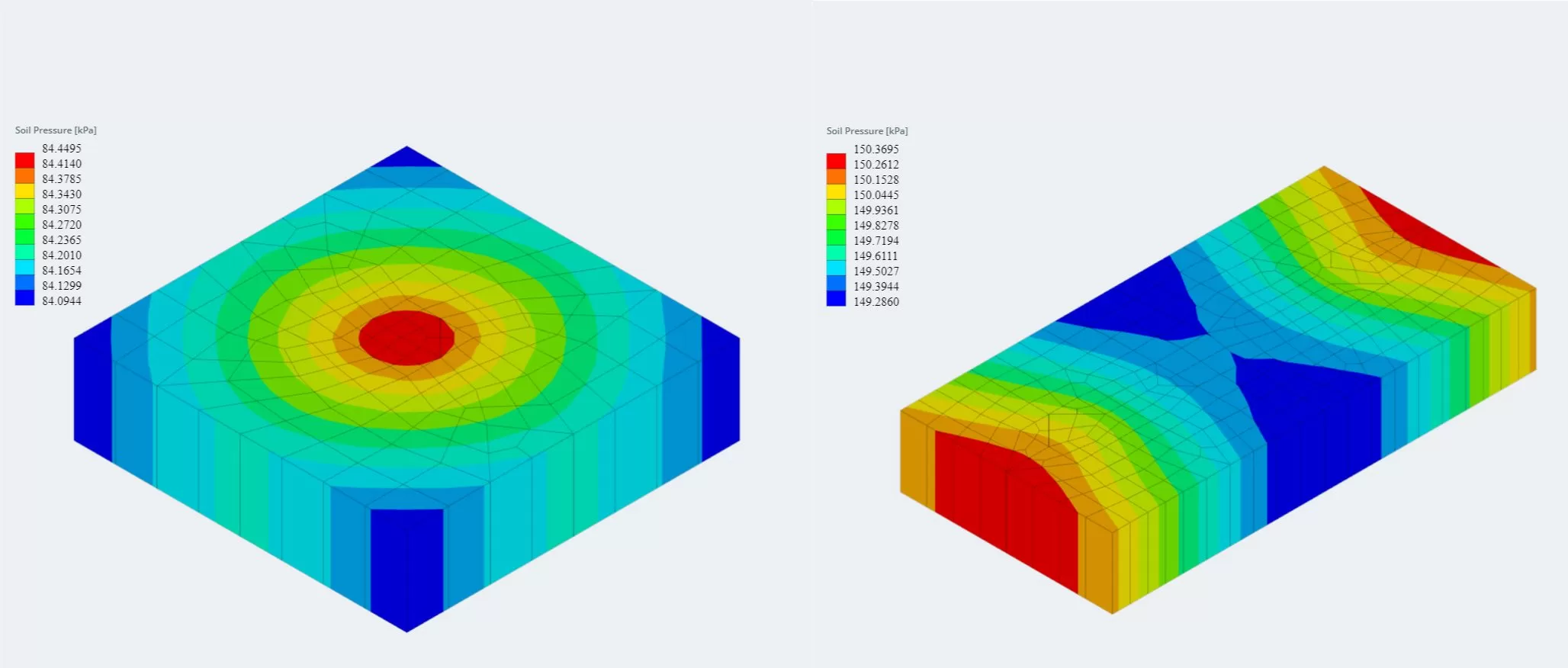
Η πιο πρόσφατη έκδοση της μονάδας θεμελίωσης είναι πλέον ενσωματωμένη στην Ανάλυση πεπερασμένων στοιχείων (ΑΣΧΗΜΟΣ), η οποία προσφέρει μια πιο ισχυρή ανάλυση πίεσης εδάφους και εισάγει την ανάλυση ξύλινου οπλισμού που θα χρησιμοποιηθεί για έναν πολύ πιο λεπτομερή έλεγχο κάμψης. Τα αποτελέσματα της FEA για την πίεση του εδάφους και τις ροπές οπλισμού ξύλου μπορούν να προβληθούν σε 3D και προστέθηκαν στις αναφορές.
Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Το δωρεάν εργαλείο μας επιτρέπει στους χρήστες να αποδίδουν συγκεκριμένοι υπολογισμοί βάσης χωρίς λήψη ή εγκατάσταση!
βιβλιογραφικές αναφορές:
- πανεμορφη, J., Ιχνος, Ν. (2017). Πλήρης αναλυτική λύση για γραμμική κατανομή πίεσης εδάφους κάτω από άκαμπτο ορθογώνιο πέλμα.
- ο, Π.Μ.. (2007). Αρχές Μηχανικής του Ιδρύματος (7ου Έκδοση). Παγκόσμια Μηχανική
- Ράβατ, ΜΙΚΡΟ., και. αλ. (2020). Απομονωμένες ορθογώνιες βάσεις κάτω από διαξονική κάμψη: Μια Κριτική Αξιολόγηση και Μεθοδολογία Απλοποιημένης Ανάλυσης.
- ακτίνα, Σ.Σ. (1995). Οπλισμένο σκυρόδεμα. Επιστήμη Blackwell
Προγραμματιστής προϊόντος
BSc (Εμφύλιος), MSc (Εμφύλιος)
