Πίνακας περιεχομένων

• Υπολογισμός διαγράμματος ροπής κάμψης
• Υπολογισμός διαγράμματος ροπής κάμψης με το χέρι
• Σημάδι Σύμβασης για Διαγράμματα Ροπής Κάμψης
• Πώς να υπολογίσετε την κάμψη χρησιμοποιώντας τη δέσμη SkyCiv

Υπολογισμός διαγράμματος ροπής κάμψης

Ακολουθούν απλές οδηγίες για τον υπολογισμό του διαγράμματος ροπής κάμψης του α απλά υποστηριζόμενη δέσμη. Μελετήστε αυτήν τη μέθοδο καθώς είναι πολύ ευέλικτη (και μπορεί να προσαρμοστεί σε πολλούς διαφορετικούς τύπους προβλημάτων. Η δυνατότητα υπολογισμού της ροπής του α δέσμη είναι μια πολύ κοινή πρακτική για δομικούς μηχανικούς και εμφανίζεται συχνά σε εξετάσεις κολεγίου και γυμνασίου. Καλό είναι να σημειωθεί νωρίς, ότι το λογισμικό SkyCiv Beam μπορεί να τα εμφανίσει υπολογισμοί χεριών άμεσα και αυτόματα! Θα ακολουθήσουμε το σημερινό σεμινάριο με ένα παράδειγμα που λαμβάνεται απευθείας από τη μονάδα υπολογισμού χειρός στο SkyCiv Beam.

Πρώτα, τι είναι ένα στιγμή κάμψηςτ? Μια στιγμή είναι μια περιστροφική δύναμη που εμφανίζεται όταν μια δύναμη εφαρμόζεται κάθετα σε ένα σημείο σε μια δεδομένη απόσταση μακριά από αυτό το σημείο. Υπολογίζεται ως η κάθετη δύναμη πολλαπλασιαζόμενη επί την απόσταση από το σημείο. Μια κάμψη στιγμή είναι απλά η κάμψη που εμφανίζεται σε μια δέσμη λόγω μιας στιγμής.

Είναι σημαντικό να θυμάστε δύο πράγματα κατά τον υπολογισμό των ροπών κάμψης; (1) οι τυπικές μονάδες είναι Nm και (2) όταν συμπιέζεται η επάνω ίνα, η κάμψη θεωρείται θετική. Με τους ορισμούς να ξεφεύγουν, ας δούμε τα βήματα για τον υπολογισμό ενός διαγράμματος ροπής κάμψης!

Υπολογιστής δωρεάν δέσμης

Υπολογισμός διαγράμματος ροπής κάμψης με το χέρι

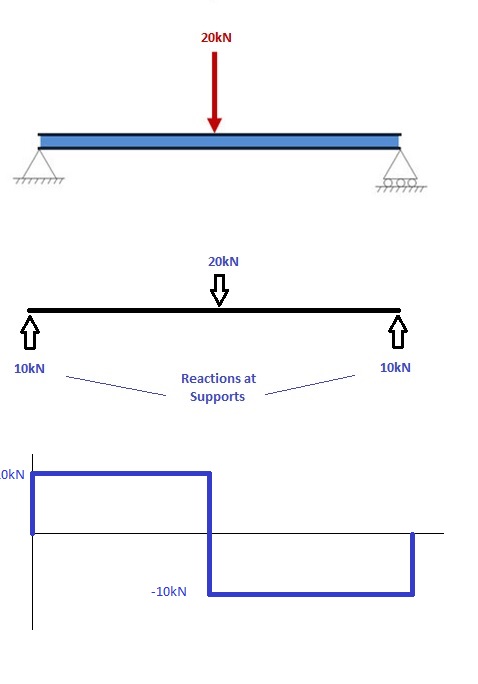
1. Υπολογίστε τις αντιδράσεις στα στηρίγματα και σχεδιάστε το ελεύθερο διάγραμμα σώματος (FBD)

Εάν δεν είστε σίγουροι πώς να το κάνετε προσδιορίστε τις αντιδράσεις στα στηρίγματα – παρακαλώ δείτε πρώτα αυτό το σεμινάριο. Μόλις έχετε τις αντιδράσεις, σχεδιάστε το δωρεάν διάγραμμα σώματος και Διάγραμμα διατμητικής δύναμης κάτω από την ακτίνα. Τέλος, ο υπολογισμός των στιγμών μπορεί να γίνει στα ακόλουθα βήματα:

2. Απο αριστερά προς δεξιά, φτιαχνω, κανω “περικοπές” πριν και μετά από κάθε αντίδραση / φορτίο

Για τον υπολογισμό της ροπής κάμψης μιας δέσμης, Πρέπει να δουλέψουμε με τον ίδιο τρόπο που κάναμε για το Διάγραμμα Δύναμης Διάτμησης. Ξεκινώντας από x = 0 θα κινηθούμε κατά μήκος της δέσμης και θα υπολογίσουμε τη ροπή κάμψης σε κάθε σημείο.

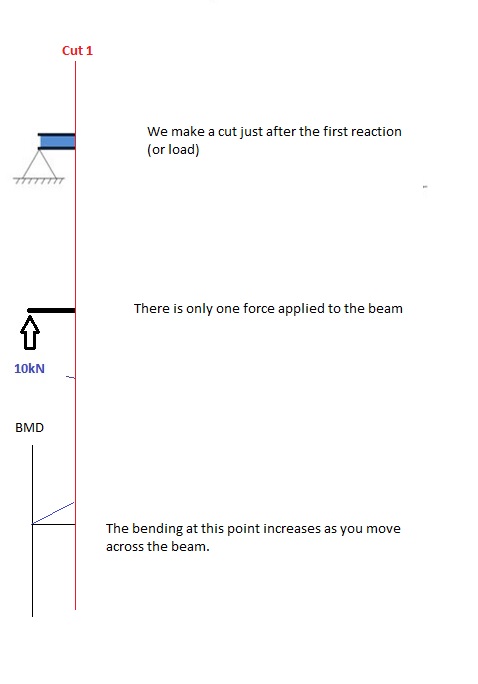
Τομή 1

Κάνει μια “Τομή” αμέσως μετά την πρώτη αντίδραση της δέσμης. Στο απλό μας παράδειγμα:

Έτσι, όταν κόβουμε τη δέσμη, θεωρούμε μόνο τις δυνάμεις που εφαρμόζονται στα αριστερά της κοπής μας. Σε αυτήν την περίπτωση, έχουμε μια δύναμη 10kN προς τα πάνω. Τώρα όπως θυμάστε, μια ροπή κάμψης είναι απλώς η δύναμη x απόσταση. Έτσι καθώς προχωράμε περισσότερο από τη δύναμη, το μέγεθος της ροπής κάμψης θα αυξηθεί. Μπορούμε να το δούμε στο BMD μας. Η εξίσωση για αυτό το μέρος του διαγράμματος ροπής ροπής είναι:

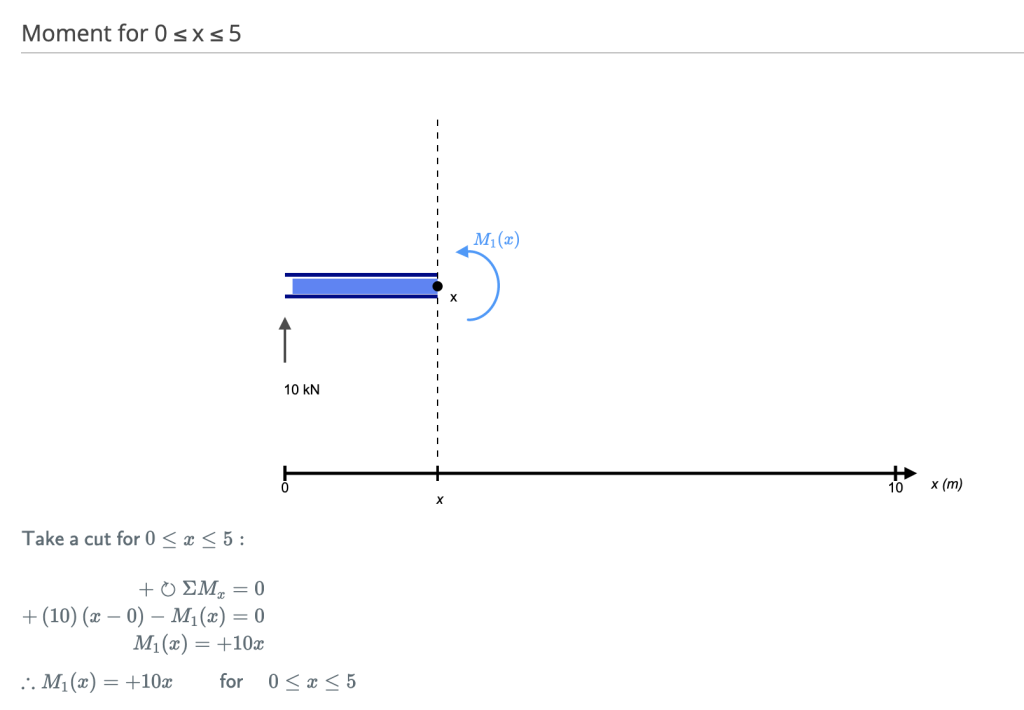
[Πηγή: SkyCiv Ενότητα υπολογισμού χειρός δοκού]

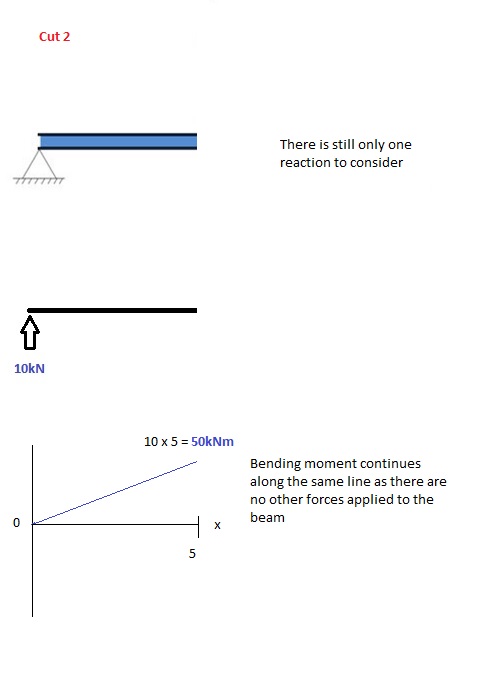
Τομή 2

Αυτή η τομή γίνεται πριν από τη δεύτερη δύναμη κατά μήκος της δέσμης. Δεδομένου ότι δεν υπάρχουν άλλα φορτία που εφαρμόζονται μεταξύ της πρώτης και της δεύτερης κοπής, ο εξίσωση ροπής κάμψης θα παραμείνει ίδια. Αυτό σημαίνει ότι μπορούμε να υπολογίσουμε τη μέγιστη ροπή κάμψης (σε αυτήν την περίπτωση στο μεσαίο σημείο, ή x = 5) αντικαθιστώντας απλώς το x = 5 στην παραπάνω εξίσωση:

Τομή 3

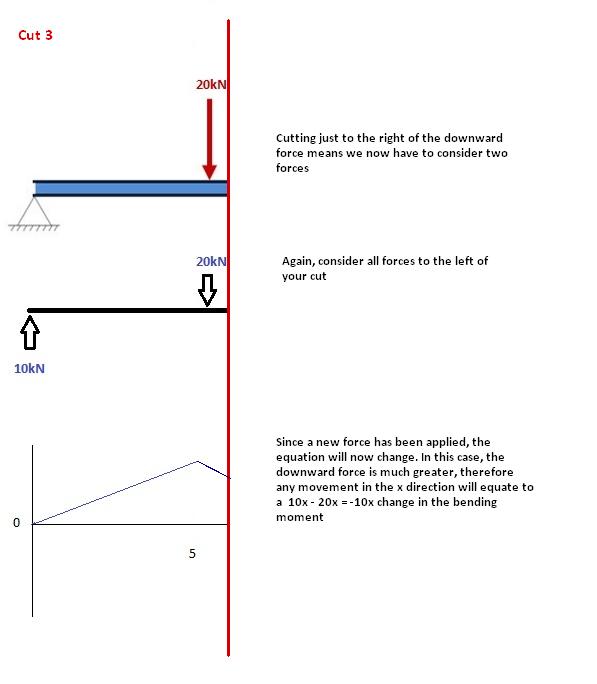
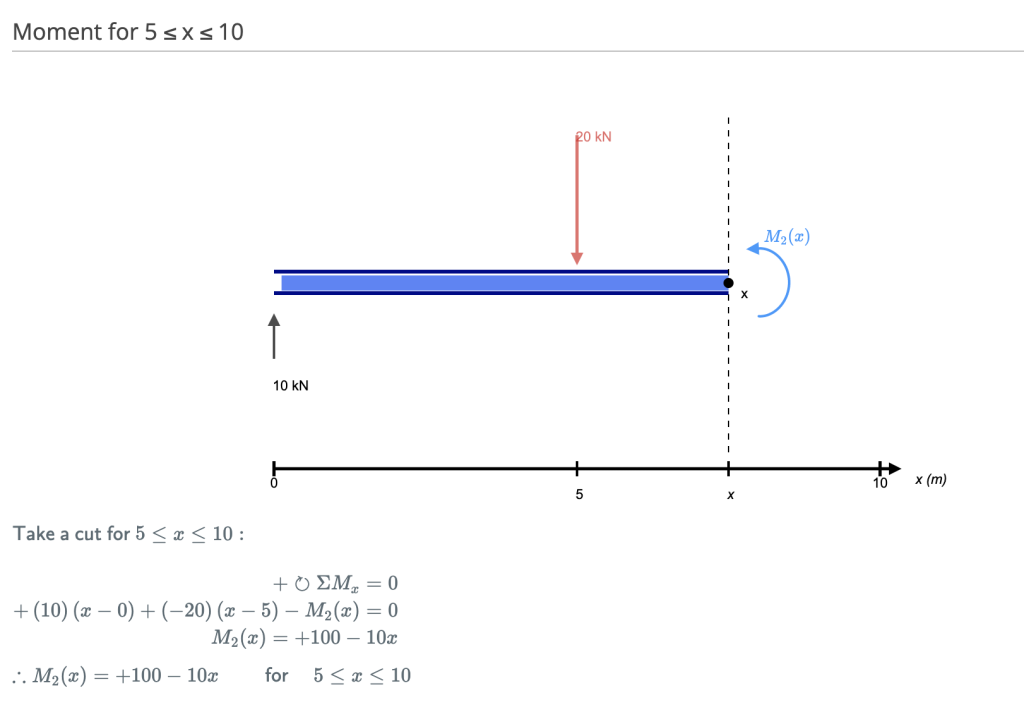
Αυτό το κόψιμο γίνεται αμέσως μετά τη δεύτερη δύναμη κατά μήκος της δέσμης. Τώρα έχουμε ΔΥΟ δυνάμεις που δρουν στα αριστερά της περικοπής μας: μια αντίδραση υποστήριξης 10kN και φορτίο -20kN προς τα κάτω. Τώρα λοιπόν πρέπει να εξετάσουμε και τις δύο αυτές δυνάμεις καθώς προχωράμε κατά μήκος της δέσμης μας. Για κάθε μετρητή κινούμαστε κατά μήκος της δέσμης, θα προστεθεί μια στιγμή + 10kNm από την πρώτη δύναμη και -20kNm από τη δεύτερη.

Έτσι μετά το σημείο x = 5, γίνεται η εξίσωση ροπής ροπής: Μ(Χ) = 50 +10(x-5) – 20(x-5) Μ(Χ) = 50 -10(x-5) Για 5 ≤ x ≤ 10 ΣΗΜΕΙΩΣΗ: Ο λόγος που γράφουμε (x-5) είναι επειδή θέλουμε να γνωρίζουμε μόνο την απόσταση από το pt x = 5. Οτιδήποτε πριν από αυτό το σημείο χρησιμοποιεί μια προηγούμενη εξίσωση.[Πηγή: SkyCiv Ενότητα υπολογισμού χειρός δοκού]

Τομή 4

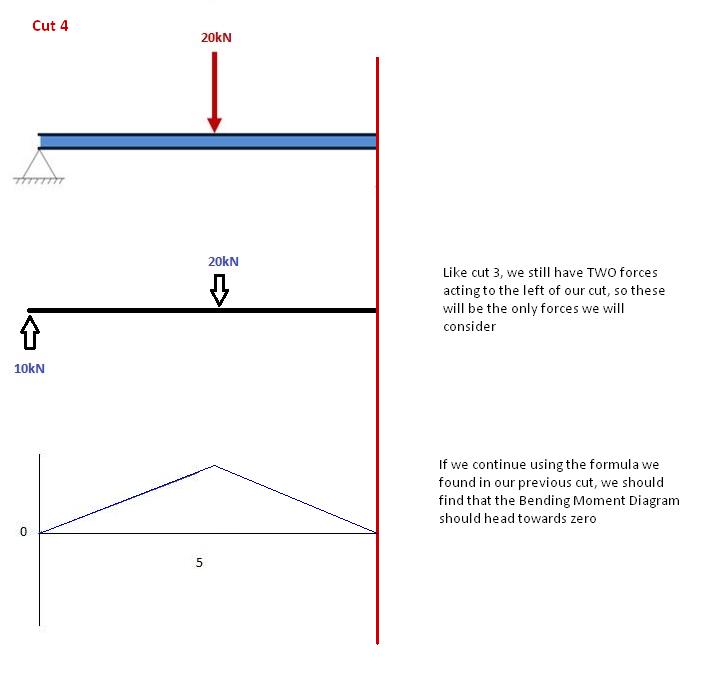
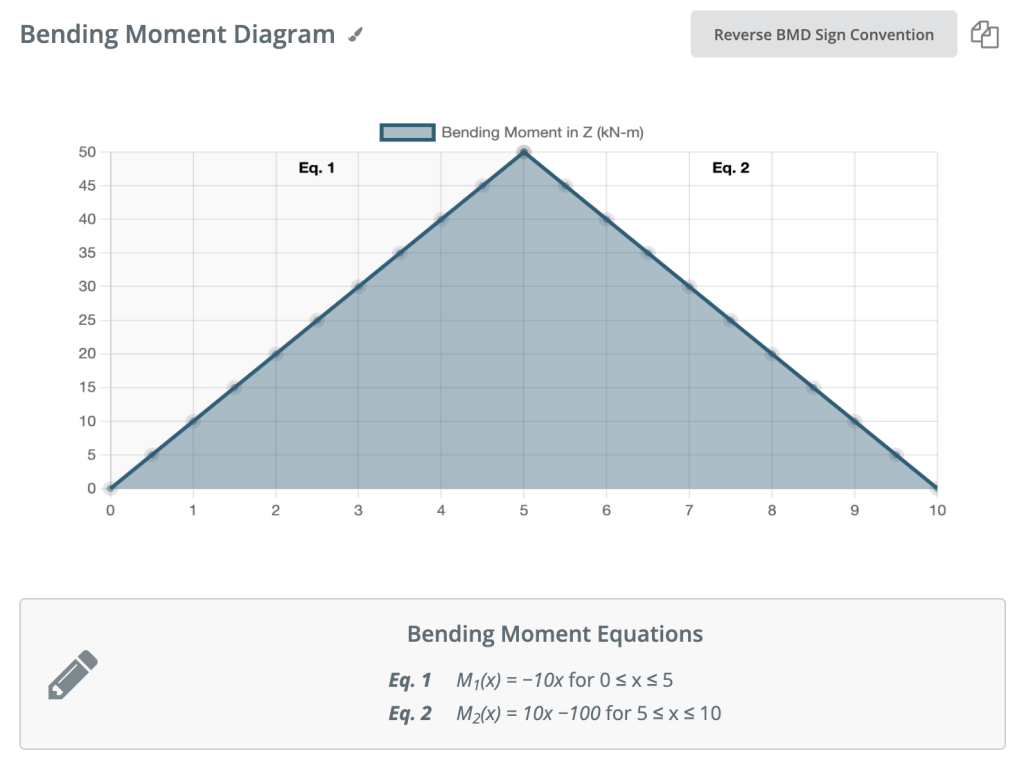
Πάλι, ας προχωρήσουμε στα δεξιά της δοκού μας και να κάνουμε μια περικοπή λίγο πριν από την επόμενη δύναμή μας. Σε αυτήν την περίπτωση, η επόμενη περικοπή μας θα συμβεί λίγο πριν την αντίδραση από το Right Support. Δεδομένου ότι δεν υπάρχουν άλλες δυνάμεις μεταξύ της υποστήριξης και της προηγούμενης περικοπής μας, η εξίσωση θα παραμείνει η ίδια: Μ(Χ) = 50 -10(x-5) Για 5 ≤ x≤ 10 Και ας αντικαταστήσουμε το x = 10 σε αυτό για να βρούμε τη στιγμή κάμψης εύρεσης στο τέλος της δέσμης: Μ(Χ) = 50 – 10(10-5) = 0kNm Αυτό έχει νόημα. Δεδομένου ότι η δέσμη μας είναι στατική (και καμία περιστροφή) έχει νόημα ότι η ακτίνα μας πρέπει να έχει μηδενικές στιγμές σε αυτό το σημείο όταν λαμβάνουμε υπόψη όλες τις δυνάμεις μας. Ικανοποιεί επίσης μία από τις αρχικές μας προϋποθέσεις, ότι το άθροισμα των στιγμών στην υποστήριξη ισούται με μηδέν. ΣΗΜΕΙΩΣΗ: Εάν οι υπολογισμοί σας οδηγούν σε οποιονδήποτε άλλο αριθμό εκτός από 0, κάνατε λάθος!

Το τελικό αποτέλεσμα, όπως εμφανίζεται στο SkyCiv Beam:

Σημάδι Σύμβασης για Διαγράμματα Ροπής Κάμψης

Συζητήσαμε πώς να βρείτε τη ροπή κάμψης παραπάνω. Τα διαγράμματα ροπής κάμψης μπορεί να μπερδευτούν κάπως όταν πρόκειται για υπογραφή συμβάσεων. Μπορεί να δείτε το ίδιο διάγραμμα σχεδιασμένο σε αντίθετες κατευθύνσεις ανάλογα με την πηγή. Η σύμβαση σημάτων που χρησιμοποιείται από το SkyCiv εμφανίζεται παρακάτω.

Θετική στιγμή κάμψης:

Εάν η ροπή κάμψης είναι θετική, η επάνω ίνα της δοκού συμπιέζεται.

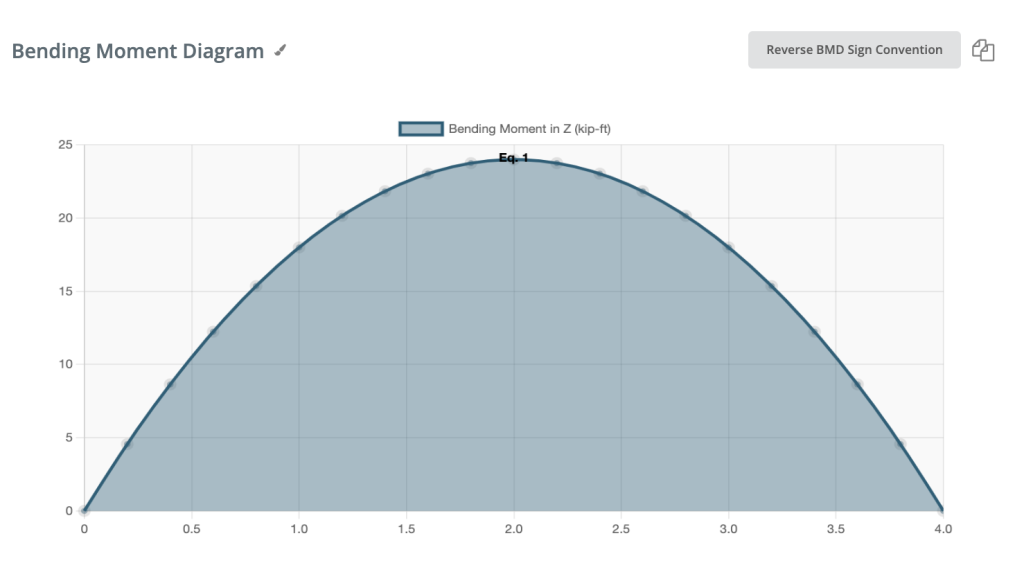
Αρνητική ροπή κάμψης:

Εάν η ροπή κάμψης είναι αρνητική, η κάτω ίνα της δοκού συμπιέζεται.

Αυτός ήταν ένας οδηγός για τον υπολογισμό των διαγραμμάτων ροπής κάμψης, αν θέλετε να μάθετε περισσότερα για αυτό το θέμα, επισκεφθείτε μας Μαθήματα Beam σελίδα. Εδώ μπορείτε να βρείτε πολλά άλλα χρήσιμα σεμινάρια όπως π.χ τύπος τάσης κάμψης ή προσδιορίστε τις αντιδράσεις στα στηρίγματα.

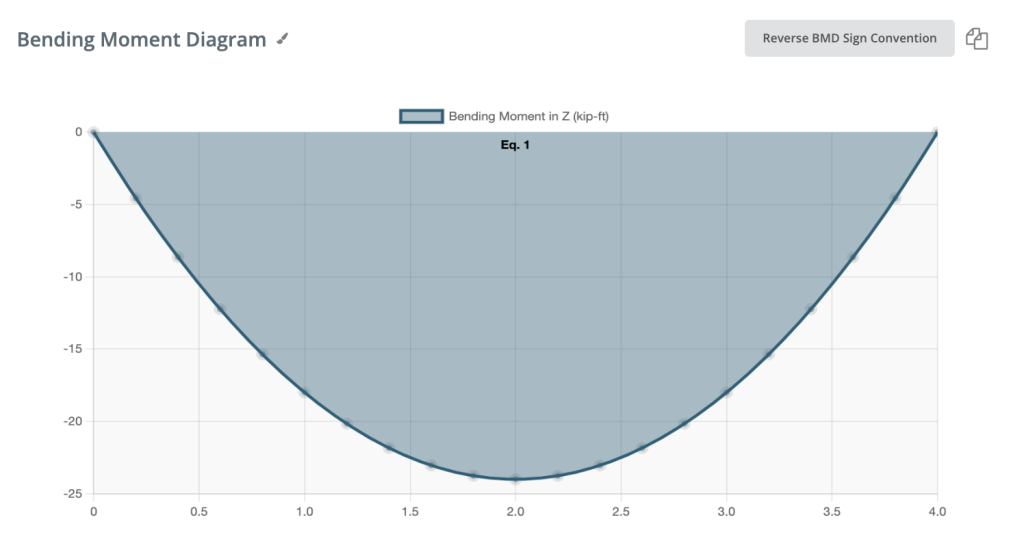
ΔΩΡΟ: Βρείτε τη στιγμή κάμψης με το SkyCiv Beam

Κάτω από την επί πληρωμή έκδοση μας SkyCiv Beam η αριθμομηχανή θα σας δείξει τους πλήρεις υπολογισμούς του χεριού και τα βήματα που έγιναν για τον υπολογισμό των διαγραμμάτων ροπής κάμψης. Απλά μοντελοποιήστε τη δέσμη σας χρησιμοποιώντας την αριθμομηχανή, και χτυπήστε λύστε. Θα σας δείξει τους υπολογισμούς βήμα προς βήμα για το πώς να σχεδιάσετε ένα διάγραμμα ροπών κάμψης (συμπεριλαμβανομένων περικοπών).