Μια αναλυτική περιγραφή και παράδειγμα υπολογισμού φορτίων χιονιού και πώς να τα εφαρμόσετε
Τα σχέδια οροφών συνήθως παρουσιάζουν πλήθος ανυψώσεων οροφής και σπάνια προσφέρουν ένα μόνο ύψος στέγης. Εξαιτίας αυτού, Υπάρχουν περιοχές στέγης υψηλότερες και χαμηλότερες μεταξύ τους και υπόκεινται σε κινήσεις χιονιού. Το ποσό του πρόσθετου φορτίου χιονιού, ή επιπλέον χρέωση, μπορεί και θα έχει μεγάλο αντίκτυπο στο σχεδιασμό των μελών σε αυτούς τους τομείς.
Η γεωμετρία της οροφής και η κατεύθυνση του ανέμου είναι οι δύο οδηγοί που οδηγούν σε κινήσεις χιονιού. Οι δύο κατευθύνσεις του ανέμου που προκαλούν χιονοστιβάδες είναι “προς τον άνεμο” και “υπήνεμος”. Ανυψώσεις χιονιού προς τα εμπρός συμβαίνουν όταν ο άνεμος φυσά χιόνι από στέγη χαμηλότερου ύψους προς τον τοίχο ενός παρακείμενου, ψηλότερη στέγη. Leeward χιονοστιβάδες συμβαίνουν όταν ο άνεμος φυσά χιόνι από μια οροφή υψηλότερου υψομέτρου κάτω σε μια γειτονική κάτω οροφή. Βλέπε σχήμα 7-7 από την ASCE 7-10 παρακάτω για μια σύντομη απεικόνιση:

Ας υποθέσουμε ότι το έργο μας είναι στο Μάντισον, Το Ουισκόνσιν και έχουμε ήδη υπολογίσει την ισορροπία μας, φορτίο χιονιού στέγης εδώ. Από το παράδειγμά μας, το φορτίο εδάφους και το επίπεδο φορτίο χιονιού οροφής βρέθηκαν να είναι 30 psf και 21 psf, αντίστοιχα. Αναλυτικές πληροφορίες σχετικά με τον τρόπο υπολογισμού της χρέωσης μετατόπισης χιονιού για κατασκευές βρίσκονται στην Ενότητα 7.8 του ASCE 7-10.
Η οροφή της δομής του παραδείγματος μας έχει δύο διαφορετικά ύψη οροφής και ως εκ τούτου πρέπει να υπολογίσουμε την επιβάρυνση μετατόπισης χιονιού και να την εφαρμόσουμε στα μέλη μας. Στην περίπτωσή μας, τα δοκάρια μας βρίσκονται σε απόσταση 10 πόδια.
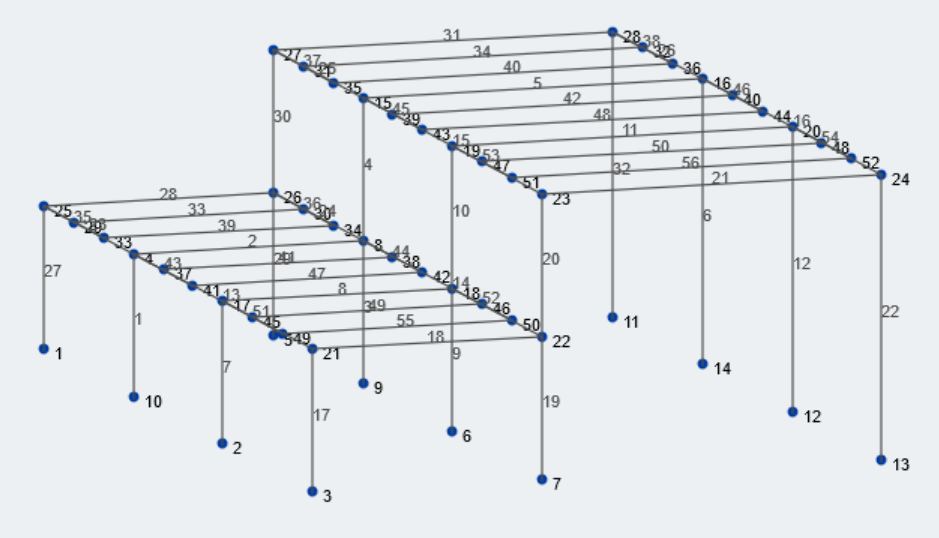
Φιγούρα 1: Ισομετρική προβολή της παραδειγματικής μας δομής
Ας συλλέξουμε πρώτα τις σχετικές γεωμετρικές πληροφορίες για τη δομή μας. Το μέγεθος του κάτω κόλπου και του άνω κόλπου είναι 25 πόδια και 37 πόδια, αντίστοιχα. Οι χαμηλότερες και υψηλότερες οροφές είναι 15 πόδια και 30 πόδια από το βαθμό, αντίστοιχα. Οι περισσότερες από τις γεωμετρικές τιμές μπορούν να συσχετιστούν με μεταβλητές. Ας ρίξουμε μια ματιά σε όλες τις σχετικές μεταβλητές για αυτόν τον υπολογισμό.
\({Π}_{σολ}\) = φορτίο χιονιού εδάφους
\({μεγάλο}_{εσύ}\) = μήκος της άνω οροφής
\({μεγάλο}_{μεγάλο}\) = μήκος της κάτω οροφής
\({η}_{ρε}\) = ύψος κλίσης χιονιού
\({β}\) = πλάτος κλίσης χιονιού
\({η}_{σι}\) = ύψος ισορροπημένου φορτίου χιονιού
\({η}_{ντο}\) = καθαρό ύψος από την κορυφή του ισορροπημένου φορτίου χιονιού έως το πλησιέστερο σημείο της γειτονικής στέγης
\({η}_{ρ}\) = διαφορά ύψους μεταξύ οροφών
\({Π}_{μικρό}\) = σχεδιασμός φορτίου χιονιού από το κεφάλαιο 7
\({γ}\) = πυκνότητα χιονιού
\({Π}_{ρε}\) = φορτίο μετατόπισης χιονιού
Ρίξτε μια ματιά στο σχήμα 7-8 από την ASCE 7-10 για μια απεικόνιση πολλών από αυτούς τους όρους και αυτό που αντιπροσωπεύουν οπτικά:
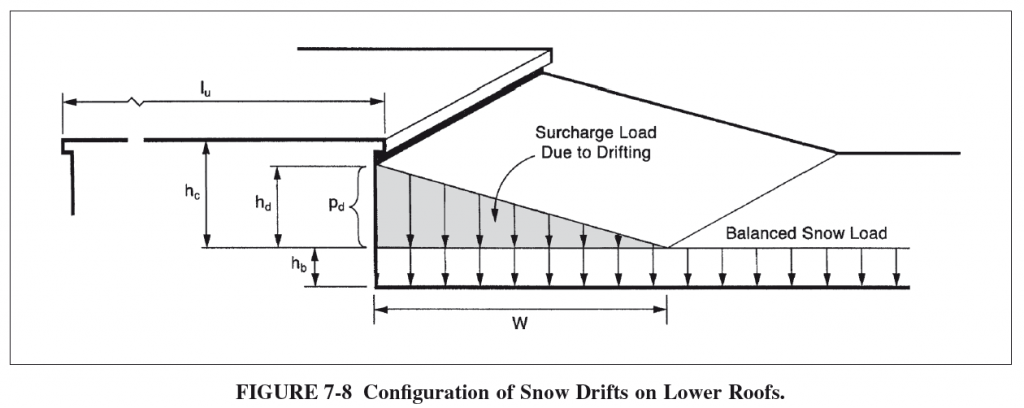
Εύρεση της προσαύξησης χρέους χιονοστιβάδας
Τώρα που έχουμε εντοπίσει ποιες είναι οι μεταβλητές, τις διαμορφώσεις φόρτωσης χιονιού, και οι γεωμετρικοί περιορισμοί της δομής μας, ας υπολογίσουμε την κλίση χιονιού.
Πρώτα, βρείτε αν είναι απαραίτητη η φόρτωση της χιονοστιβάδας, για ASCE 7.7-1:
Αν \({η}_{ντο}/{η}_{σι} < 0.2\), τότε δεν είναι απαραίτητη η εφαρμογή μετατόπισης χιονιού.
\({η}_{σι} = {Π}_{μικρό}/{γ}\), όπου:
\({γ} = 0.13{Π}_{σολ} + 14 ≤ 30 pcf\)
\({γ} = 0.13*(30) + 14 = 17.9 pcf ≤ 30 pcf \)
\({η}_{σι} = {21 psf}/{17.9 pcf } = 1.17 ft\)
\({η}_{ντο} = {η}_{ρ}-{η}_{σι}\)
\({η}_{ντο} = 15 πόδια – 1.17 ft = 13.8 ft\)
\({η}_{ντο}/{η}_{σι} = 13.8 ft / 1,17ft = 11.8 > 0.2\) και ως εκ τούτου, Απαιτείται φόρτωση με χιονοστιβάδα.
Δεύτερος, βρείτε το μέγιστο ύψος μετατόπισης μεταξύ των δύο κατευθύνσεων προς τα εμπρός και προς τα κάτω:
Το ύψος της κλίσης και για τις δύο κατευθύνσεις ανέμου μπορεί να βρεθεί χρησιμοποιώντας την εξίσωση που βρίσκεται στο Σχήμα 7-9 του ASCE 7-10, Φαίνεται παρακάτω:
\({η}_{ρε} = 3/4*(0.43({μεγάλο}_{μεγάλο})^{1/3}({σελ}+10)^{1/4}-1.5)\) για μετατόπιση προς τα εμπρός
\({η}_{ρε} = 0.43({μεγάλο}_{εσύ})^{1/3}({σελ}+10)^{1/4}-1.5\) για παρασυρόμενη παραμόρφωση
Ύψος κλίσης προς τα εμπρός:
\({η}_{ρε} = 3/4 *(0.43(25 πόδια)^{1/3}(30 psf + 10)^{1/4}-1.5)\)
\({η}_{ρε} = 1.25 ft\)
Leeward ύψος μετατόπισης:
\({η}_{ρε} = 0.43(37 πόδια)^{1/3}(30 psf + 10)^{1/4}-1.5\)
\({η}_{ρε} = 2.1 ft\)
Το μέγιστο ύψος μετατόπισης μεταξύ του ανέμου και του αριστερού ύψους μετατόπισης θα χρησιμοποιηθεί για το σχεδιασμό, επομένως:
\({η}_{ρε} = 2.1 ft\)
Επόμενο, βρείτε το πλάτος της χρέωσης μετατόπισης χιονιού:
Το πλάτος του φορτίου μετατόπισης χιονιού, \({β}\), εξαρτάται από \({η}_{ντο}\) και \({η}_{ρε}\)
Ανά τμήμα 7.7.1,
Αν \({η}_{ρε} ≤ {η}_{ντο}\), τότε \({β} = 4{η}_{ρε}\)
Αν \({η}_{ρε} > {η}_{ντο}\), τότε \({β} = 4{η}_{ρε}^ 2 /{η}_{ντο}) και στη συνέχεια \({η}_{ρε} = {η}_{ντο}\)
Στην περίπτωσή μας, \({η}_{ντο} = 13.8 ft\) και \({η}_{ρε} = 2.1 ft\), και ως εκ τούτου:
\({η}_{ρε} ≤ {η}_{ντο}\), και
\({β} = 4*(2.1 πόδια)\)
\({β} = 8.4 ft\)
Σημείωση, για ASCE 7-10 ο Το πλάτος της χιονοστιβάδας δεν υπερβαίνει ποτέ \(8{η}_{ντο}\)
τελευταίος, υπολογίστε το φορτίο χρέωσης μετατόπισης χιονιού:
Για να βρείτε τη μέγιστη επιβάρυνση, πολλαπλασιάστε το ύψος μετατόπισης με την πυκνότητα χιονιού:
\({Π}_{ρε} = {η}_{ρε}{γ}\)
Στην περίπτωσή μας,
\({Π}_{ρε} = (2.1 πόδια)*(17.9 pcf )\)
\({Π}_{ρε} = 37.6 psf\)
Στη συνέχεια, το μέγιστο φορτίο χιονοστιβάδας υπερτίθεται στο ισορροπημένο φορτίο χιονιού:
\({Π}_{Μέγιστη} = {Π}_{ρε}+{Π}_{μικρό}\)
\({Π}_{Μέγιστη} = 58.6 psf\)
Εφαρμογή των πρόσθετων επιβαρύνσεων Snow Drift
Ας δούμε το μεσαίο πλαίσιο της δομής μας. Η κατανεμημένη περιοχή για τις δοκούς σε αυτό το επίπεδο είναι 10 ft λόγω της σταθεράς 10 απόσταση δέσμης ποδιών. Φιγούρα 2 φαίνεται παρακάτω δείχνει το ισορροπημένο φορτίο χιονιού 21 Το psf εφαρμόστηκε στην οροφή της δομής μας. Σημείωση, όλες οι τιμές δεν έχουν δημιουργηθεί, φορτία υπηρεσίας.
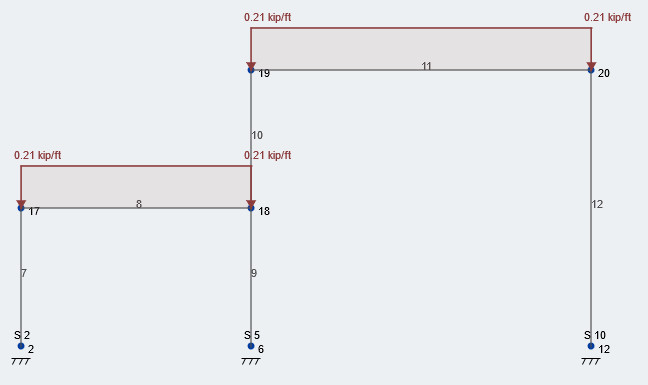
Φιγούρα 2: Τυπική κατάσταση φόρτωσης ισορροπημένου φορτίου χιονιού
Τώρα, ας πάρουμε το φορτίο επιβράδυνσης της χιονοστιβάδας και το υπερθέσουμε στη δομή μας. Φιγούρα 3 απεικονίζει το επιπλέον φορτίο μετατόπισης στη σωστή θέση. Οπως βλέπεις, το συνολικό φορτίο χιονιού είναι 58.6 psf – στρογγυλοποιήθηκε μέχρι 59 psf – βρίσκεται στην όψη του τοίχου και στη συνέχεια μειώνεται γραμμικά πάνω από το 8.4 πλάτος μετατόπισης ft στο σταθερό ισορροπημένο φορτίο χιονιού. Αυτή η κατάσταση φόρτωσης ακολουθεί ολόκληρο το μήκος του τοίχου, στην πορεία μας, το μήκος της δομής.
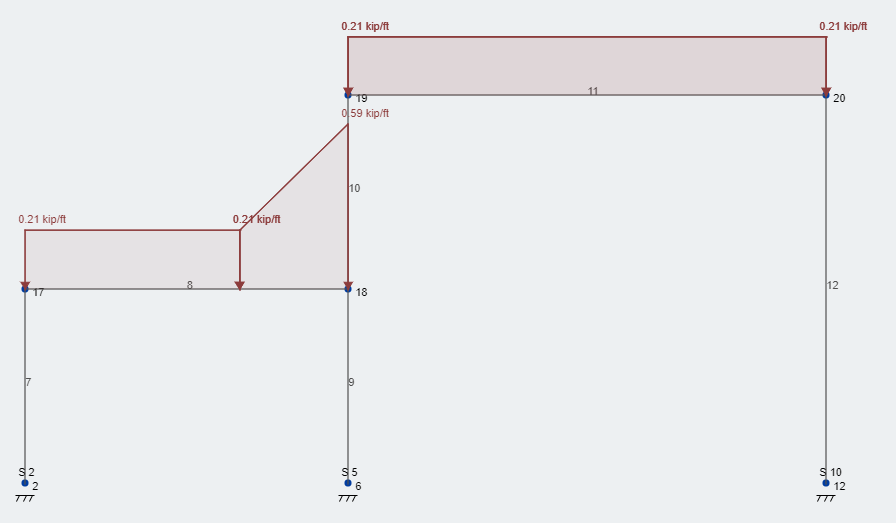
Φιγούρα 3: Τυπική φόρτωση συνθηκών φορτίου σε επίπεδο χιονιού
Σε αυτό το σημείο τα φορτία χιονιού είναι έτοιμα για ανάλυση σε συνδυασμό με άλλες περιπτώσεις φορτίων και συνδυασμούς φορτίων με βάση το ASCE 7-10 και άλλους σχετικούς κωδικούς δόμησης. Φροντίστε να διαβάσετε ολόκληρο το Κεφάλαιο 7 του ASCE 7-10 για περισσότερες πληροφορίες σχετικά με διαδοχικές διατάξεις για μερική φόρτωση χιονιού και ανισορροπημένη φόρτωση χιονιού, καθώς αυτές οι συνθήκες δεν αξιολογήθηκαν εδώ.
βιβλιογραφικές αναφορές:
- Ελάχιστα φορτία σχεδιασμού για κτίρια και άλλες κατασκευές. (2013). ΑΞΟΝΕΣ / ΕΞΙ 7-10. Αμερικανική Εταιρεία Πολιτικών Μηχανικών.


