Δωρεάν Ροπή Αδράνειας και Υπολογιστής Centroid
Υπολογίστε τη στιγμή της αδράνειας, Centroid, και Section Modulus για μεγάλη ποικιλία σχημάτων
Ένας ολοκληρωμένος οδηγός για τον υπολογιστή μας Moment of Inertia
Το SkyCiv Moment of Inertia και το Centroid Calculator σάς βοηθούν να προσδιορίσετε τη ροπή αδράνειας, κεντροειδές, και άλλες σημαντικές γεωμετρικές ιδιότητες για μια ποικιλία σχημάτων, συμπεριλαμβανομένων των ορθογωνίων, κύκλους, κοίλα τμήματα, τρίγωνα, I-Beams, Δοκοί Τ, γωνίες και κανάλια. Έχουμε επίσης μερικά άρθρα παρακάτω σχετικά με τον τρόπο υπολογισμού της ροπής αδράνειας, καθώς και περισσότερες πληροφορίες για τα κεντροειδή και το συντελεστή τομής.
Μπορείτε να επιλύσετε έως και τρεις ενότητες προτού χρειαστεί να εγγραφείτε για δωρεάν λογαριασμό - που σας δίνει επίσης πρόσβαση σε περισσότερο λογισμικό και αποτελέσματα. Ο πληρωμένος λογαριασμός μας θα δείξει τους πλήρεις υπολογισμούς με το χέρι για το πώς έφτασε το εργαλείο σε αυτό το αποτέλεσμα. Ανατρέξτε παρακάτω στην αριθμομηχανή για περισσότερες πληροφορίες σχετικά με αυτό το θέμα, καθώς και συνδέσμους προς άλλα χρήσιμα εργαλεία και δυνατότητες που μπορεί να σας προσφέρει το SkyCiv.
Πώς να χρησιμοποιήσετε τον υπολογιστή SkyCiv Moment of Inertia
Παρακολουθήστε το βίντεο επίδειξης παρακάτω για να ξεκινήσετε με την αριθμομηχανή μας.
Απλώς επιλέξτε το σχήμα διατομής που θέλετε να αξιολογήσετε από την αναπτυσσόμενη λίστα, εισαγάγετε τις διαστάσεις της ενότητας που επιλέξατε και κάντε κλικ στην επιλογή Υπολογισμός.
Αυτή η δωρεάν αριθμομηχανή πολλαπλών χρήσεων προέρχεται από το πλήρες λογισμικό μας Structural Analysis Software. Σας επιτρέπει:
- Υπολογίστε τη στιγμή της αδράνειας (Εγώ) τμήματος δοκού (Δεύτερη στιγμή της περιοχής)
- Υπολογιστής Centroid που χρησιμοποιείται για τον υπολογισμό του Centroid (ντο) στον άξονα X και Y ενός τμήματος δέσμης
- Υπολογίστε την πρώτη στιγμή της περιοχής (Στατική στιγμή αδράνειας) (Ερ) τμήματος δοκού
- Υπολογιστής μέτρου ενότητας για τον υπολογισμό του μέτρου ενότητας (ΜΕ) τμήματος δοκού
- Υπολογίστε τη σταθερά στρέψης (Ι) τμήματος δοκού
Ορισμοί ιδιοτήτων κοινής ενότητας
Η αριθμομηχανή ροπής αδράνειας θα υπολογίσει με ακρίβεια μια σειρά από σημαντικές ιδιότητες διατομής που χρησιμοποιούνται στη δομική μηχανική. Ακολουθεί μια συνοπτική λίστα με τους όρους και τους ορισμούς ιδιοκτησίας της ενότητας:
- Περιοχή τμήματος (ΕΝΑ) – Η περιοχή τομής είναι ένας αρκετά απλός υπολογισμός, αλλά χρησιμοποιείται άμεσα σε υπολογισμούς αξονικής τάσης (τόσο μεγαλύτερη επιφάνεια διατομής, τόσο μεγαλύτερη είναι η αξονική αντοχή)
- Στιγμή αδράνειας (Από, Ναι) – επίσης γνωστή ως δεύτερη στιγμή της περιοχής, είναι ένας υπολογισμός που χρησιμοποιείται για τον προσδιορισμό της αντοχής ενός μέλους και της αντοχής του στην παραμόρφωση. Όσο μεγαλύτερος είναι αυτός ο αριθμός, τόσο ισχυρότερο είναι το τμήμα. Εδώ υπάρχουν δύο άξονες:
- Μεγάλος Άξονας (Από) – Πρόκειται για τον άξονα Z και συνήθως θεωρείται ο κύριος άξονας, καθώς είναι συνήθως η ισχυρότερη κατεύθυνση του μέλους
- Ανήλικος Αξονας (Ναι) - Πρόκειται για τον άξονα Υ και θεωρείται ο δευτερεύων ή αδύναμος άξονας. Αυτό συμβαίνει επειδή τα τμήματα δεν έχουν σχεδιαστεί για να παίρνουν τόση δύναμη σε αυτόν τον άξονα
- Αξίζει επίσης να σημειωθεί ότι εάν ένα σχήμα έχει τις ίδιες διαστάσεις και στις δύο κατευθύνσεις (τετράγωνο, εγκύκλιος κλπ..) αυτές οι τιμές θα είναι ίδιες και στις δύο κατευθύνσεις. Δείτε το Moment of Ineria ενός κύκλου για να μάθετε περισσότερα.
- Centroid (Cz, Cy) – αυτό είναι το κέντρο μάζας για το τμήμα και συνήθως έχει ένα στοιχείο Z και Y. Για συμμετρικά σχήματα, αυτό θα είναι γεωμετρικό κέντρο. Για μη συμμετρικά σχήματα (όπως η γωνία, Κανάλι) αυτά θα βρίσκονται σε διαφορετικές τοποθεσίες. Μάθετε πώς να υπολογίζετε το κέντρο ενός τμήματος δοκού. Η παραπάνω αριθμομηχανή λειτουργεί και ως κεντροειδής αριθμομηχανή, υπολογισμός του κεντροειδούς Χ και Υ οποιουδήποτε τύπου σχήματος.
- Στατική στιγμή αδράνειας (Qz, Qy) – Γνωστό και ως First Moment of Area, Αυτό μετρά την κατανομή του εμβαδού ενός τμήματος δοκού από έναν άξονα. Σαν τη Στιγμή της Αδράνειας, αυτά είναι και προς την κατεύθυνση Z και Y. Αυτά χρησιμοποιούνται συνήθως σε υπολογισμούς διατμητικής τάσης, οπότε όσο μεγαλύτερη είναι αυτή η τιμή τόσο ισχυρότερη είναι η τομή έναντι της διάτμησης. Η αριθμομηχανή θα παρέχει αυτήν την τιμή, αλλά κάντε κλικ εδώ για να μάθετε περισσότερα σχετικά με τον υπολογισμό της πρώτης στιγμής του εμβαδού.
- Μέτρο ελαστικής τομής (Sz, Sy στην Αμερική. Zz, Zy στη Βρετανία ή την Αυστραλία) – Γνωστό και ως συντελεστής στατικής διατομής, και χρησιμοποιούνται σε υπολογισμούς τάσεων κάμψης. Συνήθως υπολογίζονται στο πάνω και κάτω τμήμα ινών. Για παράδειγμα, Szt είναι ο συντελεστής τομής γύρω από τον άξονα Z στην επάνω ίνα του τμήματος.
- Σταθερότητα στρέψης (Ι) - επίσης γνωστή ως πολική ροπή αδράνειας ή J, είναι μια τιμή που περιγράφει την αντίσταση ενός υλικού στη συστροφή ή τη στρεπτική παραμόρφωση.
- Το Μέτρο Πλαστικής Τομής (μικρό) - μια μέτρηση της ικανότητας ενός σχήματος διατομής να αντιστέκεται στην κάμψη του πλαστικού, χρησιμοποιείται για την εκτίμηση της τάσης ενός υλικού όταν αρχίζει να υποχωρεί (φτάσει το πλαστικό του όριο) κάτω από ένα συγκεκριμένο φορτίο και χρησιμοποιείται συνήθως για το σχεδιασμό και την ανάλυση δοκών υπό φορτίο.
Άλλες παράμετροι – Αυτά είναι πιο προηγμένα αποτελέσματα που υπολογίζονται από το πλήρες πρόγραμμα δημιουργίας ενοτήτων SkyCiv:
- Προϊόν Αδράνειας (σχετικά με τον άξονα Z και Y): Ένα μέτρο της αντίστασης ενός σχήματος στην περιστροφή γύρω από έναν συγκεκριμένο άξονα, ίσο με το εγκάρσιο γινόμενο της απόστασης από τον άξονα σε οποιοδήποτε σημείο του σχήματος και την αντίστοιχη συνιστώσα της ροπής αδράνειας του σημείου.
- Μέτρο πλαστικού τμήματος (σχετικά με τον άξονα Z και Y): Ένα μέτρο της ικανότητας ενός σχήματος διατομής να αντιστέκεται στην πλαστική κάμψη, χρησιμοποιείται για την εκτίμηση της τάσης ενός υλικού όταν αρχίζει να υποχωρεί (φτάσει το πλαστικό του όριο) κάτω από ένα συγκεκριμένο φορτίο.
- Πλαστικός ουδέτερος άξονας (σχετικά με τον άξονα Z και Y): Άξονας σε σχήμα διατομής από τον οποίο πρέπει να περάσουν όλες οι δυνάμεις που ασκούν το σχήμα για να προκληθεί πλαστική παραμόρφωση.
- Περιοχή διάτμησης (σχετικά με τον άξονα Z και Y): Το εμβαδόν ενός σχήματος διατομής που είναι αποτελεσματικό στην αντίσταση των δυνάμεων διάτμησης.
- Απόσταση κέντρου διάτμησης έως Centroid (και στον άξονα Z και Y): Η αριθμομηχανή κέντρου SkyCiv βοηθά στον υπολογισμό της απόστασης μεταξύ του κέντρου διάτμησης και του κέντρου ενός σχήματος διατομής.
- Σταθερότητα στρέψης (Χρήση FEA): Μια τιμή που περιγράφει την αντίσταση ενός υλικού στη συστροφή ή τη στρεπτική παραμόρφωση, υπολογίζεται με χρήση της ανάλυσης πεπερασμένων στοιχείων.
- Ακτίνα στρέψης: Η απόσταση από έναν άξονα στον οποίο πρέπει να συγκεντρωθεί το εμβαδόν ενός σχήματος διατομής για να οδηγήσει στην ίδια σταθερά στρέψης με το πραγματικό σχήμα.
- Στρεβλώνοντας σταθερά: Μια τιμή που περιγράφει την αντίσταση ενός υλικού σε παραμόρφωση ή παραμόρφωση.
- Μονοσυμμετρία σταθερά (σχετικά με τον άξονα Z και Y): Ένα μέτρο του πόσο συμμετρικό είναι ένα σχήμα διατομής ως προς έναν συγκεκριμένο άξονα, με τιμή μηδέν που δείχνει τέλεια συμμετρία.
- Ακτίνα περιστροφής (σχετικά με τον άξονα Z και Y): Η απόσταση από έναν άξονα στον οποίο πρέπει να συγκεντρωθεί το εμβαδόν ενός σχήματος διατομής για να οδηγήσει στην ίδια ροπή αδράνειας με το πραγματικό σχήμα.
- Γωνία περιστροφής του άξονα αρχής: Η γωνία μεταξύ του ουδέτερου άξονα και του κύριου άξονα ενός σχήματος διατομής.
Σχετικά με τη στιγμή της αδράνειας, Centroids και άλλες ιδιότητες ενότητας
Συγκεντρώσαμε επίσης περισσότερες πληροφορίες για τον υπολογισμό της ροπής αδράνειας των τομών. Αυτός ο πλήρης οδηγός θα βοηθήσει στην παροχή μιας ολοκληρωμένης βάσης γνώσεων για όλα τα πράγματα που σχετίζονται με τη ροπή αδράνειας, κεντροειδή, συντελεστής τομής και άλλες σημαντικές ιδιότητες γεωμετρικής τομής. Στα παρακάτω τμήματα, συμπεριλαμβάνουμε τη ροπή αδράνειας, πώς να υπολογίσετε το κέντρο, ροπή αδράνειας και κοινές εξισώσεις MOI με τη βοήθεια του SkyCiv Moment of Inertia και του Centroid Calculator.
Τι είναι η Ροπή Αδράνειας?
Η στιγμή της αδράνειας (πιο τεχνικά γνωστή ως η ροπή αδράνειας της περιοχής, ή τη δεύτερη στιγμή της περιοχής) είναι μια σημαντική γεωμετρική ιδιότητα που χρησιμοποιείται στη δομική μηχανική. Σχετίζεται άμεσα με την αντοχή του υλικού που έχει το τμήμα σας.
Γενικά μιλώντας, Λεπτομερής ανάλυση, τόσο περισσότερη δύναμη έχει το τμήμα σας, και κατά συνέπεια τόσο λιγότερο θα εκτρέπεται υπό φορτίο. Η Ροπή Αδράνειας ενός ορθογωνίου, Λεπτομερής ανάλυση, είναι τεχνικά μια μέτρηση του πόση ροπή απαιτείται για να επιταχυνθεί η μάζα γύρω από έναν άξονα - εξ ου και η λέξη αδράνεια στο όνομά της.
Πώς να βρείτε τη στιγμή της αδράνειας - Ορθογώνιος
Να υπολογίσετε τη ροπή αδράνειας ενός ορθογωνίου, μπορείτε να χρησιμοποιήσετε τον τύπο:
Ι = (σι * h^3) / 12
I είναι η ροπή αδράνειας του ορθογωνίου
b είναι το πλάτος του ορθογωνίου
h είναι το ύψος του ορθογωνίου
Είναι σημαντικό να σημειωθεί ότι η μονάδα μέτρησης για τα b και h πρέπει να είναι συνεπής (π.χ., ίντσες, χιλιοστά, και τα λοιπά.). Επίσης, η μονάδα του τελικού αποτελέσματος εξαρτάται από τη μονάδα εισόδου, για παράδειγμα αν η είσοδος είναι σε μέτρο, τότε η μονάδα αποτελέσματος θα ήταν m^4.
Παράδειγμα Υπολογισμός Ροπής Αδράνειας
Ας πούμε ότι έχουμε ένα ορθογώνιο με τις παρακάτω διαστάσεις:
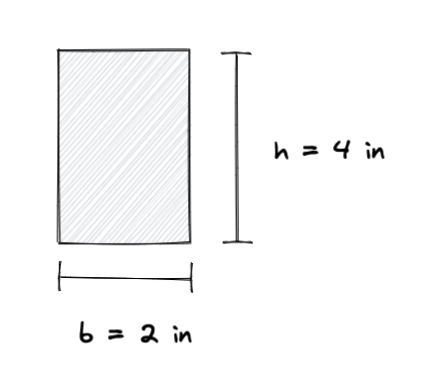
Χρησιμοποιώντας τον τύπο για ροπή αδράνειας, μπορούμε να υπολογίσουμε τη ροπή αδράνειας του ορθογωνίου ως εξής:
Ι = (σι * h^3) / 12
Ι = (2 * 4^ 3) / 12
Ι = (2 * 64) / 12
= 10.67 σε^4
Άρα η ροπή αδράνειας του ορθογωνίου είναι 10.67 ίντσα^4. Αυτή η ροπή αδράνειας είναι γύρω από τον κεντροειδές άξονα, να θυμάστε ότι εάν χρειάζεται να βρείτε τη ροπή αδράνειας ως προς έναν διαφορετικό άξονα, θα χρειαστεί να χρησιμοποιήσετε διαφορετικό τύπο ή να εκτελέσετε έναν μετασχηματισμό. Μπορείτε επίσης να ελέγξετε ότι η μονάδα είναι πάντα το γινόμενο της ισχύος της μονάδας εισόδου, σε αυτήν την περίπτωση όλες οι μονάδες εισόδου είναι ίντσες, οπότε το αποτέλεσμα είναι σε ίντσες^4.
Μπορούμε να επαληθεύσουμε αυτό το αποτέλεσμα με τον παραπάνω υπολογιστή ελεύθερης ροπής αδράνειας, που δείχνει το ίδιο αποτέλεσμα του 10.6667 σε^4:
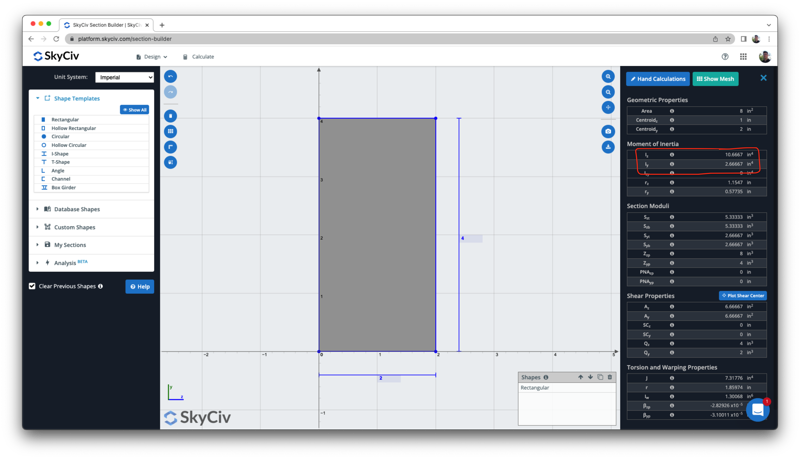
Πώς να βρείτε τη στιγμή της αδράνειας - Είμαι δοκός
Τώρα ας δούμε μια πιο περίπλοκη περίπτωση όπου η διατομή είναι μια δοκός I, με διαφορετικές διαστάσεις φλάντζας. Το concept είναι το ίδιο, Ωστόσο, η προσέγγιση σε αυτή την περίπτωση είναι αρκετά διαφορετική. Βασικα, πρέπει να δούμε την ακτίνα I ως συνδυασμό διαφορετικών ορθογωνίων και να αθροίσουμε τα διαφορετικά μέρη για να λάβουμε τα τμήματα πλήρη Ροπή Αδράνειας. Εν συντομία, πρέπει να ακολουθήσουμε αυτά τα τρία βήματα:
- Υπολογίστε τον Ουδέτερο Άξονα για ολόκληρο το τμήμα
- Υπολογίστε το MOI κάθε τμήματος
- Υπολογίστε τη ροπή αδράνειας χρησιμοποιώντας το Θεώρημα του Παράλληλου Άξονα - που είναι ουσιαστικά το άθροισμα των επιμέρους ροπών αδράνειας
Ας εξετάσουμε λοιπόν την παρακάτω ενότητα:
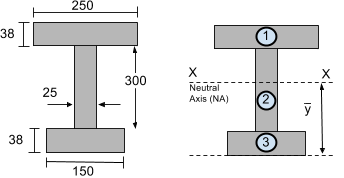
Ο Ουδέτερος Άξονας (ΝΑ) βρίσκεται στο κέντρο. Αυτός είναι ουσιαστικά ένας σταθμισμένος μέσος όρος της περιοχής και της απόστασης από το κάτω μέρος για κάθε τμήμα. Απλώς πρέπει να χρησιμοποιήσουμε την εξίσωση του κέντρου για τον υπολογισμό του κατακόρυφου (και) κεντροειδές σχήμα πολλών τμημάτων.

Θα πάρουμε το σημείο αναφοράς ή τη γραμμή αναφοράς από το κάτω μέρος του τμήματος δοκού. Τώρα ας βρούμε τα Ai και yi για κάθε τμήμα του τμήματος I-beam που φαίνεται παραπάνω, έτσι ώστε να μπορεί να βρεθεί το κατακόρυφο ή το κέντρο y.


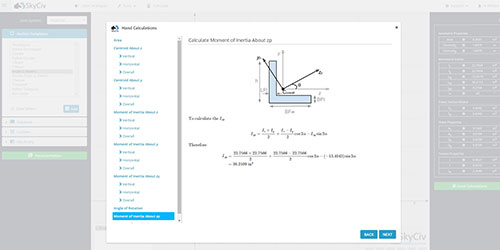
Τώρα έχουμε το κέντρο. Μπορούμε να συνεχίσουμε να υπολογίζουμε τη ροπή αδράνειας. Για να υπολογίσουμε τη συνολική ροπή αδράνειας της ενότητας πρέπει να χρησιμοποιήσουμε το "Παράλληλο θεώρημα άξονα" όπως ορίζεται παρακάτω:

Αφού το έχουμε χωρίσει σε τρία ορθογώνια μέρη, πρέπει να υπολογίσουμε τη ροπή αδράνειας καθενός από αυτούς τους τομείς. Μπορούμε τώρα να χρησιμοποιήσουμε τον τύπο απλοποιημένης ορθογώνιας ροπής αδράνειας:
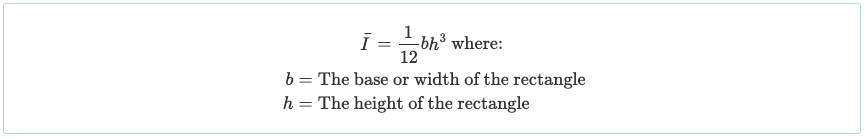
Τώρα έχουμε όλες τις πληροφορίες που χρειαζόμαστε για να χρησιμοποιήσουμε το "Παράλληλο θεώρημα άξονα" και βρείτε τη συνολική ροπή αδράνειας του τμήματος I-beam. Στη στιγμή της αδράνειας παράδειγμα:

Αλλη μια φορά, μπορούμε να συγκρίνουμε αυτό το αποτέλεσμα με αυτό του υπολογιστή αδράνειας ελεύθερης ροπής για να συγκρίνουμε τα αποτελέσματα τόσο του κέντρου όσο και της ροπής αδράνειας, όπου τόσο το κέντρο (216.29 σε) και στιγμή αδράνειας (4.74 x 10^8 σε ^4) αγώνας:
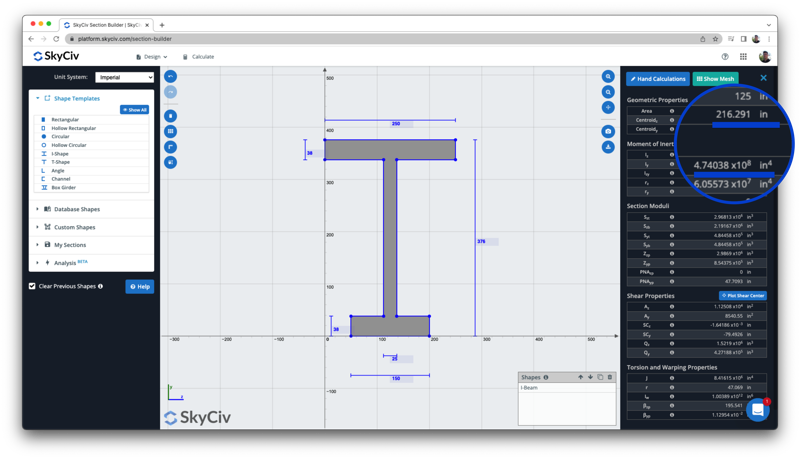
Εξισώσεις Ροπής Αδράνειας
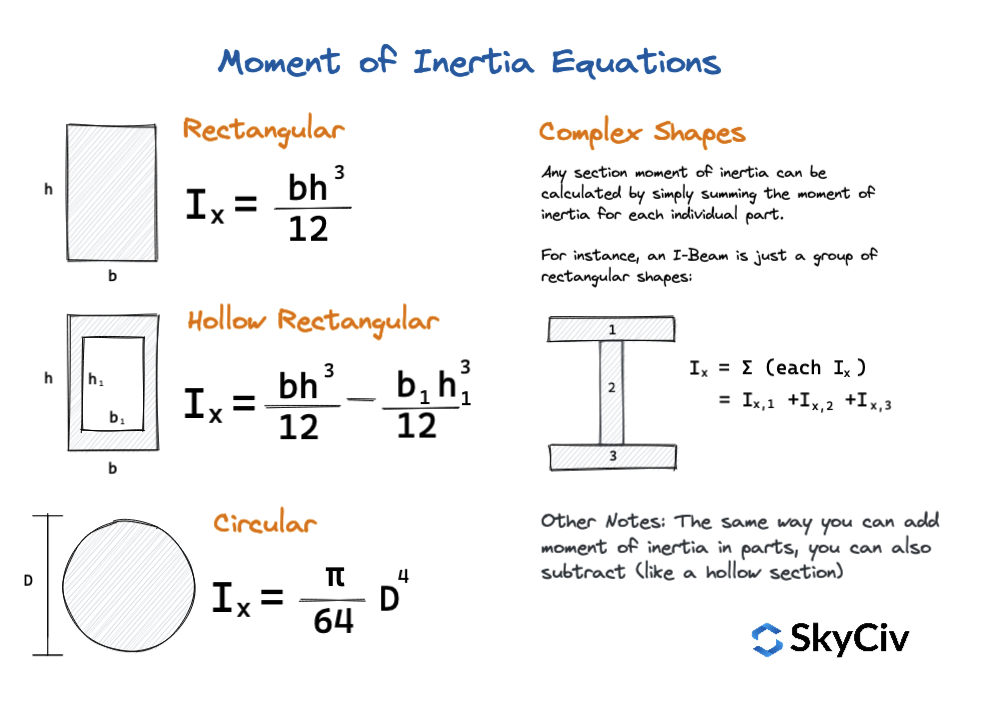
Απλές εξισώσεις μπορούν επίσης να χρησιμοποιηθούν για τον υπολογισμό της Ροπής Αδράνειας κοινών σχημάτων και τομών. Αυτές είναι εξισώσεις γρήγορης αδράνειας που παρέχουν γρήγορες τιμές και είναι ένας πολύ καλός τρόπος για να διασταυρώσετε την αναφορά ή να ελέγξετε τα αποτελέσματά σας. Εστιάζοντας μόνο σε απλά σχήματα, Το παρακάτω διάγραμμα δείχνει μερικές από αυτές τις εξισώσεις:
SkyCiv Centroid Αριθμομηχανή
Ένα κέντρο, γνωστό και ως «γεωμετρικό κέντρο», είναι το κέντρο μάζας ενός αντικειμένου με ομοιόμορφη πυκνότητα. Μια απλοποιημένη επίδειξη ενός κέντρου, θα ήταν η θέση στην οποία θα χρειαστεί να τοποθετήσετε ένα μολύβι για να ισορροπήσει στο δάχτυλό σας. Η θέση στην οποία το μολύβι είναι ισορροπημένο και δεν πέφτει από το δάχτυλό σας θα ήταν η κατά προσέγγιση θέση του κέντρου του μολυβιού. Λαμβάνει υπόψη τη μάζα και την πυκνότητα του υλικού για να καθορίσει το σημείο όπου η μάζα του μολυβιού είναι ίση και στις δύο πλευρές του δακτύλου σας, και επομένως αντιπροσωπεύει το «κέντρο μάζας» του μολυβιού.
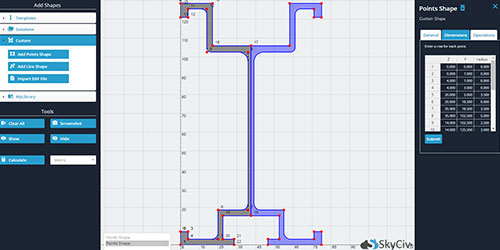
Ο υπολογιστής SkyCiv Centroid χρησιμοποιεί FEA για να παρέχει αποτελέσματα υψηλής ακρίβειας σε δευτερόλεπτα, όσο περίπλοκο κι αν είναι το σχήμα. Στην premium έκδοση, οι χρήστες μπορούν να εισάγουν τις συντεταγμένες των σημείων που ορίζουν το σχήμα και η αριθμομηχανή μας θα σας δώσει τις συντεταγμένες του κέντρου. Αυτό περιλαμβάνει τη δυνατότητα σχεδίασης προσαρμοσμένων σχημάτων μέσω εισαγωγής DXF, πολλαπλούς (συσσωρευμένη) σχήματα και προσαρμοσμένα σχήματα σημείων.
Εκτός από την ταχύτητα και την ακρίβειά του, Η centroid αριθμομηχανή μας είναι επίσης απίστευτα εύκολη στη χρήση. Με απλή διεπαφή χρήστη, μπορείτε να εισαγάγετε τις διαστάσεις της ενότητας σας και να λάβετε τις τιμές ιδιοτήτων ενότητας (συμπεριλαμβανομένου του κέντρου τμήματος δοκού) μέσα σε δευτερόλεπτα. Είτε εργάζεστε σε ένα σχέδιο σχεδιασμού, πειραματισμός με διαφορετικά τμήματα ή μελέτη για εξετάσεις, το SkyCiv Centroid Calculator είναι το τέλειο εργαλείο για να σας βοηθήσει να ολοκληρώσετε τη δουλειά.
Υπολογιστής μέτρου ενότητας
Όπως σημειώθηκε προηγουμένως, Αυτό το δωρεάν εργαλείο σάς παρέχει επίσης έναν υπολογισμό της μονάδας ελαστικής διατομής, Ωστόσο, εάν ξεκινάτε ως μηχανικός, μπορεί να μην καταλάβετε τι είναι το Section Modulus. Να το θέσω απλά, ο συντελεστής τομής είναι μια ιδιότητα διατομής μιας διατομής που μετρά την αντίσταση στην κάμψη και υπολογίζεται ως ο λόγος της ροπής αδράνειας προς την απόσταση από τον ουδέτερο άξονα στην πιο απομακρυσμένη ίνα. Ο συντελεστής ελαστικής τομής αναπαρίσταται σε αυτή την εξίσωση ως απλά:
Οπου,
- S είναι ο συντελεστής τομής
- I είναι η ροπή αδράνειας του τμήματος ως προς τον ουδέτερο άξονα
- y είναι η απόσταση από τον ουδέτερο άξονα μέχρι το πιο απομακρυσμένο σημείο της τομής
Υπάρχουν δύο είδη Section Modulus: Ελαστικό και Πλαστικό. Στην Αμερική, Το S χρησιμοποιείται συνήθως για να αναφέρεται στο συντελεστή ελαστικής διατομής ενώ το Z χρησιμοποιείται για να αναφέρεται στο μέτρο πλαστικής διατομής. Στη Βρετανία και την Αυστραλία, αυτά συνήθως αντιστρέφονται. Ο συντελεστής ελαστικής τομής αναφέρεται συνήθως με το γράμμα Z, ενώ το Μέτρο Πλαστικής Τομής αναφέρεται με γράμμα S.
Γενικά, το Elastic Section Modulus χρησιμοποιείται για τη σχεδίαση τομών επειδή είναι εφαρμόσιμο μέχρι το σημείο διαρροής για τα περισσότερα μέταλλα. Τα μέταλλα δεν είναι συνήθως σχεδιασμένα για να υπερβαίνουν το σημείο διαρροής του υλικού.
Πρόσθετη Τεκμηρίωση
Ανατρέξτε στις ακόλουθες σελίδες τεκμηρίωσης για πιο λεπτομερείς πληροφορίες σχετικά με τη ροπή αδράνειας, πώς να τα υπολογίσετε για διάφορα σχήματα, και πώς να χρησιμοποιήσετε την αριθμομηχανή centroid:
Διατίθενται περισσότερα δωρεάν εργαλεία
Το SkyCiv προσφέρει επίσης άλλα εργαλεία όπως το εργαλείο μεγέθους δοκού και δωρεάν λογισμικό δομικού σχεδιασμού. Το συρτάρι δυναμικής ενότητας θα σας δείξει επίσης μια γραφική αναπαράσταση του τμήματος δέσμης. Αν λοιπόν θέλετε να υπολογίσετε τη ροπή αδράνειας του κύκλου, ροπή αδράνειας ορθογωνίου ή οποιουδήποτε άλλου σχήματος, μη διστάσετε να χρησιμοποιήσετε το παρακάτω λογισμικό ή το all-inclusive SkyCiv Section Builder.
Το SkyCiv προσφέρει ένα ευρύ φάσμα λογισμικού ανάλυσης και σχεδιασμού Cloud Structural για μηχανικούς. Ως μια συνεχώς εξελισσόμενη εταιρεία τεχνολογίας, δεσμευόμαστε να καινοτομούμε και να προκαλούμε υπάρχουσες ροές εργασίας για να εξοικονομήσουμε χρόνο στους μηχανικούς στις διαδικασίες εργασίας και τα σχέδιά τους.
Χρειάζεστε περισσότερη λειτουργικότητα?
Αναβάθμιση σε α επαγγελματικό σχέδιο για να ξεκλειδώσετε πλήρη χαρακτηριστικά