Γενική περιγραφή
Το SkyCiv διαθέτει μια στιβαρή και προηγμένη μονάδα για το σχεδιασμό πλακών από οπλισμένο σκυρόδεμα. Για πρόσβαση σε αυτή τη δυνατότητα, πρέπει πρώτα να έχετε δημιουργήσει ένα μοντέλο στο SkyCiv S3D και μετά να καλέσετε τη μονάδα για αυτόματο υπολογισμό με διαφορετικούς κωδικούς κατασκευής όπως ACI-318, Ευρωπαϊκά και Αυστραλιανά Πρότυπα, και ούτω καθεξής. Ο πρωταρχικός σκοπός της μονάδας για το σχεδιασμό της πλάκας είναι να παρέχει την ποσότητα οπλισμού οπλισμού χάλυβα κατά μήκος της πλάκας.
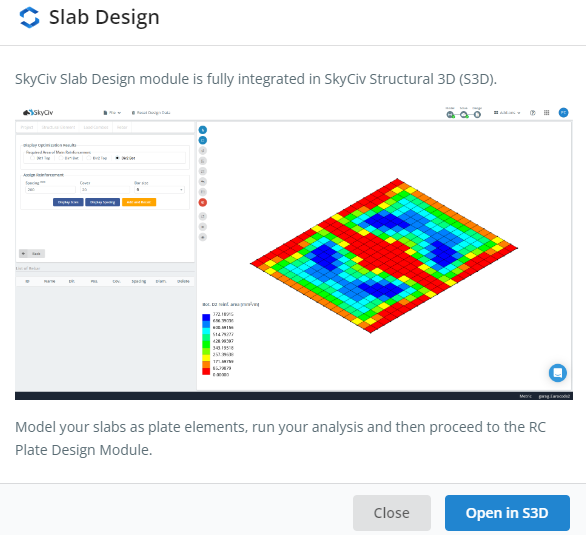
Φιγούρα 1. Ενότητα σχεδίασης πλακών SkyCiv
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
Η τεκμηρίωση SkyCiv παρέχει εξαιρετικό περιεχόμενο, συμπεριλαμβανομένων παραδειγμάτων και περιπτώσεων ανάλυσης, τόσο για εκμάθηση αν είστε νέος στις ενότητες όσο και για σύγκριση των αποτελεσμάτων από την ενότητα σχεδίασης πλάκας με υπολογισμούς με το χέρι. Μη διστάσετε να ελέγξετε τα παραδείγματα σχεδίασής μας σύμφωνα με ACI-318, Ευρωκώδικας, και AS3600.
Σας προτείνουμε να διαβάσετε αυτό το άρθρο πριν αναλύσετε σε βάθος πολύπλοκα συστήματα πλακών. Εδώ, θα μάθετε πώς διαφέρουν οι ροπές κάμψης ανάλογα με τις διαστάσεις της κάτοψης της πλάκας. Υπάρχουν δύο περιπτώσεις μελέτης, πλάκες μονής και διπλής κατεύθυνσης. Έτσι, ας αρχίσουμε να διαβάζουμε!
Συμπεριφορά μονόδρομης έναντι αμφίδρομης πλάκας
Ας εξετάσουμε το παράδειγμα πλάκας στην παρακάτω εικόνα, όπου υπάρχει στήριξη σε κάθε άκρη της πλάκας, και καθιερώνουμε ότι αυτό θα συμπεριφέρεται ως αμφίδρομη πλάκα, αυτό είναι, έχοντας μια ροπή κάμψης στις δύο κύριες κατευθύνσεις του σχεδίου.
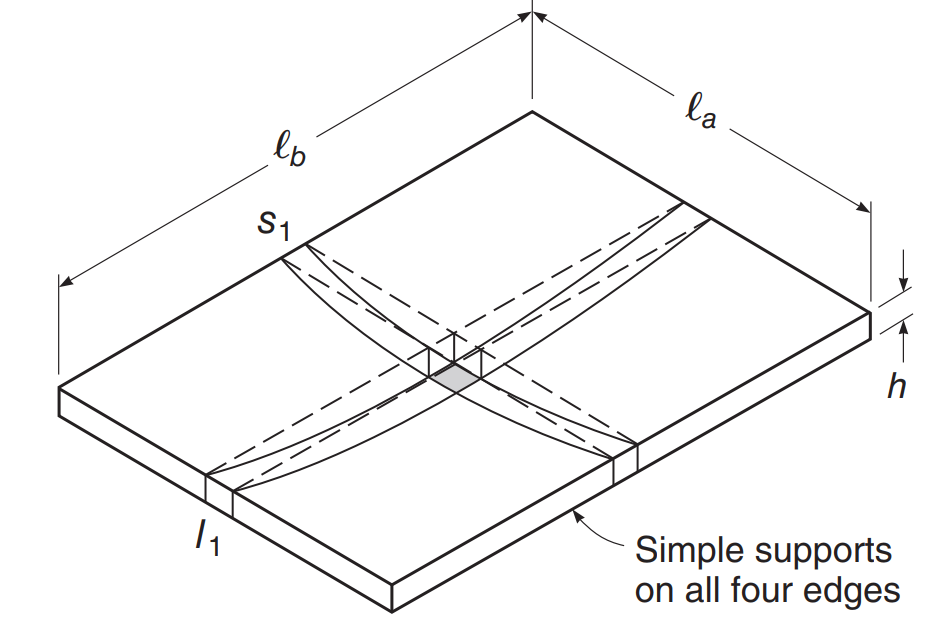
Φιγούρα 2. Απλή αμφίδρομη πλάκα παράδειγμα σε κάμψη. (Ντέιβιντ Δαρβίνος, Charles W.Dolan, Άρθουρ Χ. Nilson, “Σχεδιασμός Κατασκευών Σκυροδέματος,” Δέκατη πέμπτη Έκδοση, Εκπαίδευση McGraw-Hill)
Μπορούμε να ορίσουμε την κατακόρυφη μετατόπιση ως (\(λα < l_b \)):
\(\Delta_a = frac{{5}{w_a}{l_a^4}}{384{μι}{Εγώ}}\)
\(\Delta_b = frac{{5}{w_b}{l_b^4}}{384{μι}{Εγώ}}\)
Λόγω του ότι η πλάκα είναι ένα συνεχές σύστημα, Και οι δύο κατακόρυφες παραμορφώσεις θα έχουν την ίδια τιμή. Μπορούμε να συγκρίνουμε τις εξισώσεις για να εκφράσουμε μια σχέση μεταξύ του φορτίου που μεταφέρεται από κάθε κατεύθυνση ως συνάρτηση των διαστάσεων της κάτοψης.
\(\Delta_a = Delta_b to frac{{5}{w_a}{l_a^4}}{384{μι}{Εγώ}} = frac{{5}{w_b}{l_b^4}}{384{μι}{Εγώ}}\)
\(\frac{w_a}{w_b} = {(\frac{l_b}{λα}})^ 4 \)
Όλες οι αναφορές από οπλισμένο σκυρόδεμα για το σχεδιασμό πλάκας χωρίζονται σε μονόδρομες και αμφίδρομες εάν το πηλίκο του \(\frac{l_b}{λα}\) είναι μεγαλύτερη ή μικρότερη από μια τιμή του 2, αντίστοιχα.
Χρησιμοποιώντας τις παραπάνω εξισώσεις, πότε \(\frac{l_b}{λα}=2), το φορτίο που μεταφέρεται από τη σύντομη κατεύθυνση είναι ίσο με \(w_a = {16}{w_b}\) και όταν η τιμή είναι \(\frac{l_b}{λα}=1), το φορτίο κατανέμεται εξίσου και προς τις δύο κατευθύνσεις \(w_a ={w_b}\).
Στιγμές μονόδρομων πλακών
Έτσι, μπορούμε να δούμε ότι όταν το πηλίκο των διαστάσεων είναι μεγαλύτερο από 2, πρακτικά, όλα τα φορτία και οι ροπές κάμψης θα συγκεντρωθούν μόνο στη μικρή κατεύθυνση. Αυτή η περίπτωση είναι η μονόδρομη συμπεριφορά της πλάκας, και η μέγιστη ροπή κάμψης μπορεί να ληφθεί ως απλά υποστηριζόμενη δοκός με ενιαίο πλάτος.
\(Μ_{Μέγιστη,1,ρε}= frac{{w_a}{1 Μ}{l_a^2}}{8}\)
Στιγμές διπλής κατεύθυνσης πλάκες
Η λύση της περίπτωσης της αμφίδρομης πλάκας είναι ένα σύνθετο και προκλητικό πρόβλημα στη δομική μηχανική. Μπορείτε να δείτε στο παρακάτω σχήμα η γενική ανάλυση αποτελείται από μια πλάκα με ολόκληρες δυνάμεις και ροπές σε κάθε κατεύθυνση.
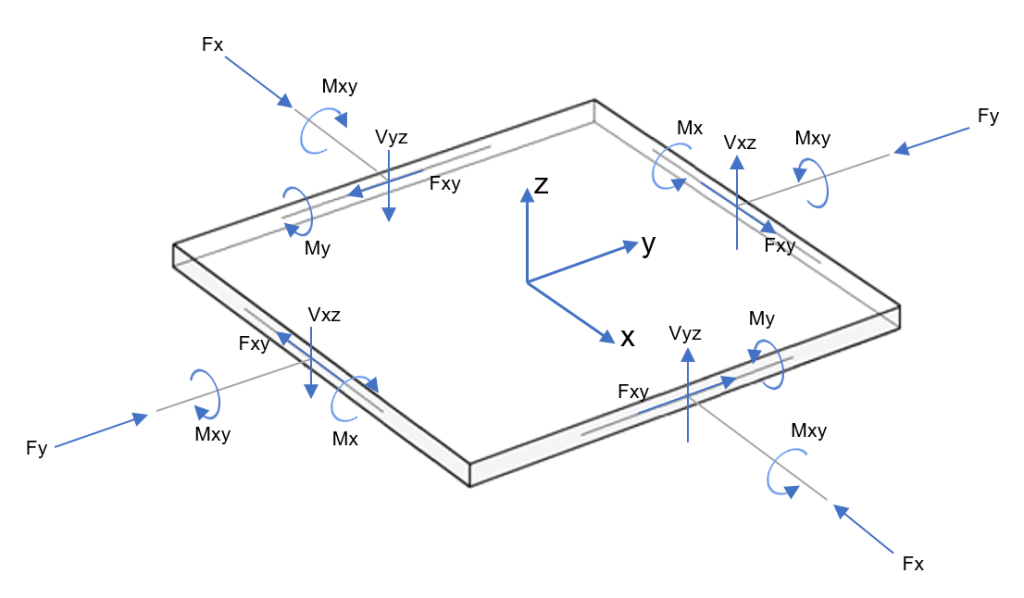
Φιγούρα 3. Ενέργειες στο στοιχείο πλάκας (ροπές κάμψης και στρέψης; κανονικές και διατμητικές δυνάμεις)
Αυτή η δυσκολία προέρχεται από το πραγματικό πρόβλημα που πρέπει να λυθεί είναι μια μερική διαφορική εξίσωση τέταρτης τάξης που περιλαμβάνει την κάμψη σε δύο κατευθύνσεις. Το σχήμα αυτής της εξίσωσης είναι:
\(\frac{\μερική^4{β}}{{\μερικός}{x^4}} + {2}\frac{{\μερική^4}{β}}{{{\μερικός}{x^2}}{{\μερικός}{y^2}}}+\frac{\μερική^4{β}}{{\μερικός}{x^4}}-\frac{f_z}{ρε} = 0\)
Όπου η ακαμψία της πλάκας (χρησιμοποιώντας τις ελαστικές μηχανικές και γεωμετρικές ιδιότητες) είναι \(D=frac{{μι}{t^3}}{{12}{(1-\όχι^2)}}\).
Η αναλυτική λύση αυτής της εξίσωσης είναι διαθέσιμη μόνο για απλές συνθήκες υποστήριξης. Ο μόνος τρόπος για να επιτευχθεί μια πιθανή λύση για πρακτικές και πραγματικές ζωντανές περιπτώσεις είναι μέσω αριθμητικών μεθόδων όπως η μέθοδος πεπερασμένων στοιχείων.
Το SkyCiv χρησιμοποιεί αυτήν την προσέγγιση για να λύσει την ανάλυση πλακών. Στους παρακάτω συνδέσμους, θα έχετε πρόσβαση σε σεμινάρια για να μάθετε για τα χαρακτηριστικά της πλατφόρμας SkyCiv: Σχεδιασμός πιάτων σε S3D και Πώς να μοντελοποιήσετε πιάτα? .
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!


