Ένα πλήρως επεξεργασμένο παράδειγμα υπολογισμού φορτίου ανέμου για πινακίδες χρησιμοποιώντας EN 1991-1-4
Σε αυτό το άρθρο, θα συζητήσουμε πώς να υπολογίσουμε τα φορτία ανέμου στις πινακίδες χρησιμοποιώντας το EN 1991-1-4 βρίσκεται στο Oxfordshire, Ηνωμένο Βασίλειο. Οι αναφορές μας θα είναι το ΕΝ 1991-1-4 Δράση στις δομές (φορτίο ανέμου) και ΒΣ ΕΝ 1991-1-4 Εθνικό Παράρτημα. Θα χρησιμοποιήσουμε παρόμοια δεδομένα σε ΣΕ 1991-1-4 Παράδειγμα υπολογισμού φορτίου ανέμου.
Το SkyCiv αυτοματοποιεί τους υπολογισμούς της ταχύτητας του ανέμου με μερικές παραμέτρους. Δοκιμάστε μας Υπολογιστής φορτίου ανέμου πινακίδας:
Δεδομένα δομής
Σε αυτό το παράδειγμα, θα χρησιμοποιήσουμε τα παρακάτω δεδομένα. Θα εξετάσουμε μόνο κατεύθυνση πηγής ανέμου ίση με 240°. Εξάλλου, ο Το υψόμετρο του εδάφους της τοποθεσίας είναι 57,35μ.
Τραπέζι 1. Τα δεδομένα πινακίδας που χρειάζονται για τον υπολογισμό του φορτίου ανέμου.
| Τοποθεσία | Oxfordshire, Ηνωμένο Βασίλειο |
| Χωρητικότητα | Διάφορα – Πινακίδα αγγελίας |
| Εδαφος | Επίπεδη χωράφια |
| Σημάδι οριζόντια διάσταση, σι | 12.0 Μ |
| Σημάδι Οριζόντια Κατακόρυφη, η |
12.0 Μ |
| Από το έδαφος μέχρι την κορυφή της πινακίδας, Η |
50.0Μ |
| Κέντρο από γείωση σε πινακίδα, μεμι |
44.0 Μ |
| Περιοχή αναφοράς της πινακίδας Ασημάδι |
144.0 τ.μ.. |
| Διάμετρος πόλου, ρε |
1.0 Μ |
| Τύπος επιφάνειας πόλων |
Χυτοσίδηρος |
| Από το έδαφος μέχρι την κορυφή του στύλου, μεσολ |
38.0 Μ |
| Περιοχή αναφοράς του στύλου ΑΠόλος |
38.0 Μ |
Φιγούρα 1. Τοποθεσία ιστότοπου (από τους Χάρτες Google).

Φιγούρα 2. Διαστάσεις πινακίδας.
Ο τύπος για τον προσδιορισμό της πίεσης του ανέμου είναι:
Για βασική ταχύτητα ανέμου:
\({β}_{σι} = {ντο}_{σε εσένα} {ντο}_{εποχή} {ντο}_{alt} {β}_{σι,χάρτης}\) (1)
Οπου:
\({β}_{σι}\) = βασική ταχύτητα ανέμου σε m / s
\({ντο}_{σε εσένα}\) = κατευθυντικός παράγοντας
\({ντο}_{εποχή}\)= εποχιακός παράγοντας
\({ντο}_{alt}\)= συντελεστής υψομέτρου όπου:
\({ντο}_{alt} = 1 + 0.001ΕΝΑ \) Για \( z ≤ 10 \) (2)
\({ντο}_{alt} = 1 + 0.001ΕΝΑ ({10/με}^{0.2}) \) Για \( με > 10 \) (3)
\({β}_{σι,χάρτης}\) = θεμελιώδης τιμή της βασικής ταχύτητας ανέμου που δίνεται στο σχήμα NA.1 του BS EN 1991-1-4 Εθνικό Παράρτημα
\( ΕΝΑ \) = υψόμετρο της τοποθεσίας σε μέτρα πάνω από τη μέση επιφάνεια της θάλασσας
Για βασική πίεση ταχύτητας:
\({ε}_{σι} = 0.5 {⍴}_{αέρας} {{β}_{σι}}^{2} \) (4)
Οπου:
\({ε}_{σι}\) = σχεδιασμός πίεσης ανέμου σε Pa
\({⍴}_{αέρας}\) = πυκνότητα αέρα (1.226kg / κ.μ.)
\({β}_{σι}\)= βασική ταχύτητα ανέμου σε m / s
Για μέγιστη πίεση:
\({ε}_{Π}(με) = 0.5 {ντο}_{μι}(με){ε}_{σι} \) για τοποθεσία στο έδαφος της χώρας (5)
\({ε}_{Π}(με) = 0.5 {ντο}_{μι}(με){ντο}_{μι,Τ}{ε}_{σι} \) για τοποθεσία στο έδαφος της πόλης (6)
Οπου:
\({ντο}_{μι}(με)\) = παράγοντας έκθεσης
\({ντο}_{μι,Τ} \) = συντελεστής διόρθωσης έκθεσης για το έδαφος της πόλης
Για να υπολογίσετε τη δύναμη του ανέμου που ενεργεί στην πινακίδα/στύλο:
\({φά}_{β} = {ντο}_{μικρό}{ντο}_{ρε}{ντο}_{φά}{ε}_{Π}({με}_{μι}){ΕΝΑ}_{αναφ} \) (7)
Οπου:
\( {ντο}_{μικρό} {ντο}_{ρε} \) = δομικός παράγοντας
\({ντο}_{φά} \) = συντελεστής δύναμης της κατασκευής
\({ε}_{Π}({με}_{μι}) \) = πίεση μέγιστης ταχύτητας στο ύψος αναφοράς \({με}_{μι} \)
\({ΕΝΑ}_{αναφ} = b h) = περιοχή αναφοράς της κατασκευής
Κατηγορία εδάφους
Με βάση το BS EN 1991-1-4 Εθνικό Παράρτημα, τις Κατηγορίες Εδάφους στην ΕΝ 1991-1-14 συγκεντρώθηκαν σε 3 κατηγορίες: Κατηγορία εδάφους 0 αναφέρεται ως Θάλασσα; Οι κατηγορίες εδάφους I και II έχουν θεωρηθεί ως Έδαφος χώρας, και οι κατηγορίες εδάφους III και IV έχουν θεωρηθεί ως έδαφος πόλης.
Λαμβάνοντας υπόψη τον άνεμο που προέρχεται από 240°, μπορούμε να κατατάξουμε την κατηγορία εδάφους του ανάνεου εδάφους ως Το έδαφος της πόλης.
Παράγοντες κατεύθυνσης και εποχής, \({ντο}_{σε εσένα}\) & \({ντο}_{εποχή}\)
Για τον υπολογισμό της εξίσωσης (1), πρέπει να καθορίσουμε τους παράγοντες κατεύθυνσης και εποχής, \({ντο}_{σε εσένα}\) & \({ντο}_{εποχή}\). Από τον Πίνακα ΝΑ.1 του ΒΣ ΕΝ 1991-1-4 Εθνικό Παράρτημα, αφού η κατεύθυνση της πηγής του ανέμου είναι 240°, την αντίστοιχη τιμή για τον συντελεστή κατεύθυνσης, \({ντο}_{σε εσένα}\), είναι ίσο με 1.0.

Αφ 'ετέρου, θέλουμε να εξετάσουμε μια συντηρητική περίπτωση για τον παράγοντα της εποχής, \({ντο}_{εποχή}\), που θα το κάνουμε αριθμομηχανή φορτίου ανέμου 1.0.
Συντελεστής Υψόμετρου \({ντο}_{alt}\)
Για τον παράγοντα υψόμετρο, \({ντο}_{alt}\), θα χρησιμοποιήσουμε μόνο την Εξίσωση (2) για μια πιο συντηρητική προσέγγιση χρησιμοποιώντας την ανύψωση της τοποθεσίας \( ΕΝΑ \) ίσο με 57,35μ. Επομένως:
\({ντο}_{alt} = 1 + 0.001(57.35) = 1.05735\)
Βασική ταχύτητα και πίεση ανέμου, \({β}_{σι}\) & \({ε}_{σι}\)
Ο χάρτης ταχύτητας ανέμου για το Ηνωμένο Βασίλειο μπορεί να ληφθεί από το σχήμα NA.1 του Εθνικού Παραρτήματος για BS EN 1991-1-4.
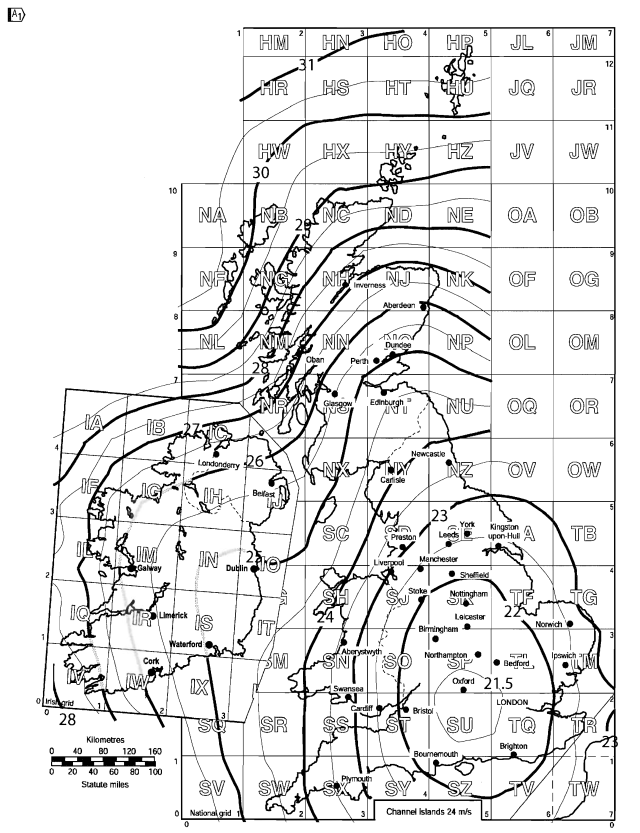
Φιγούρα 5. Βασική ταχύτητα ανέμου για το Ηνωμένο Βασίλειο με βάση το σχήμα NA.1 του BS EN 1991-1-4 Εθνικό Παράρτημα.
Για την τοποθεσία του ιστότοπού μας, Oxfordshire, Αγγλία, το υπολογισμένο \( {β}_{σι,χάρτης} \) είναι ίσο με 22.7 Κυρία.
\( {β}_{σι} = {ντο}_{σε εσένα} {ντο}_{εποχή} {ντο}_{alt} {β}_{σι,χάρτης} = (1.0)(1.0)(1.05735)(22.7) \)
\( {β}_{σι} = 24.0 Κυρία \)
Μπορούμε να υπολογίσουμε τη βασική πίεση ανέμου, \( {ε}_{σι,0} \), χρησιμοποιώντας εξισώσεις (4):
\( {ε}_{σι} = 0.5(1.226)({24}^{2}) = 353.09 Καλά \)
Το SkyCiv αυτοματοποιεί τώρα την ανίχνευση της περιοχής ανέμου και λαμβάνει την αντίστοιχη τιμή ταχύτητας ανέμου με λίγες μόνο εισόδους. Δοκιμάστε μας Εργαλείο ανέμου SkyCiv Free
Παράγοντας ορογραφίας \({ντο}_{ο}(με)\)
Για αυτήν τη δομή, το έδαφος είναι σχετικά επίπεδο για τον άνεμο που έρχεται από 240°, ο
συντελεστής υψομέτρου, \({ντο}_{alt}\), θα χρησιμοποιήσουμε μόνο την Εξίσωση (2) για μια πιο συντηρητική προσέγγιση χρησιμοποιώντας την ανύψωση της τοποθεσίας \( ΕΝΑ \) ίσο με 57,35μ. Επομένως:
Πίεση μέγιστης ταχύτητας, \({ε}_{Π}(με)\)
Για τη δομή μας, δεδομένου ότι η κατηγορία εδάφους ταξινομείται ως έδαφος της πόλης, η κορυφή Ομοίως, η πίεση της μέγιστης ταχύτητας, \({ε}_{Π}(με)\), μπορεί να λυθεί χρησιμοποιώντας την εξίσωση (6):
\({ε}_{Π}(με) = {ντο}_{μι}(με){ντο}_{μι,Τ}{ε}_{σι} \)
Οπου:
\({ντο}_{μι}(με)\) = παράγοντας έκθεσης με βάση το σχήμα NA.7 του BS EN 1991-1-4 Εθνικό Παράρτημα
\({ντο}_{μι,Τ} \) = συντελεστής διόρθωσης έκθεσης για το έδαφος της πόλης με βάση το Σχήμα NA.8 του BS EN 1991-1-4 Εθνικό Παράρτημα
Για τον προσδιορισμό του παράγοντα έκθεσης, \({ντο}_{μι}(με)\) , για την πινακίδα, πρέπει να υπολογίσουμε το \(με – {η}_{δισ}\) και η απόσταση από τον άνεμο προς την ακτή σε km. Για απλότητα, θα ορίσουμε το ύψος μετατόπισης, \({η}_{δισ}\), προς το 0. Για το \(με \) αξίες, θα το εξετάσουμε \(z = 38.0\) και \(z = 44.0\). Εξάλλου, η απόσταση από τον άνεμο μέχρι την ακτή είναι μεγαλύτερη από 100 χιλιόμετρα. Επομένως, χρησιμοποιώντας το σχήμα ΝΑ.7 του BS EN 1991-1-4 Εθνικό Παράρτημα:
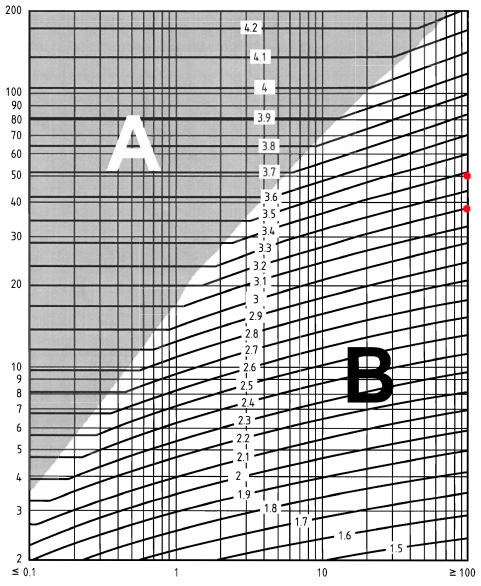
Φιγούρα 6. Εικόνα ΝΑ.7 του BS EN 1991-1-4 Εθνικό Παράρτημα.
Επομένως:
\({ντο}_{μι}(38.0) = 3.2\)
\({ντο}_{μι}(44.0) = 3.3\)
Αφ 'ετέρου, ο συντελεστής διόρθωσης έκθεσης \( {ντο}_{μι,Τ} \) για την πινακίδα μπορεί να προσδιοριστεί από το σχήμα ΝΑ.8 του BS EN 1991-1-4 Εθνικό Παράρτημα. Χρησιμοποιώντας απόσταση εντός πόλης ίση με 1km, μπορούμε να πάρουμε τον παράγοντα διόρθωσης έκθεσης \( {ντο}_{μι,Τ} \):
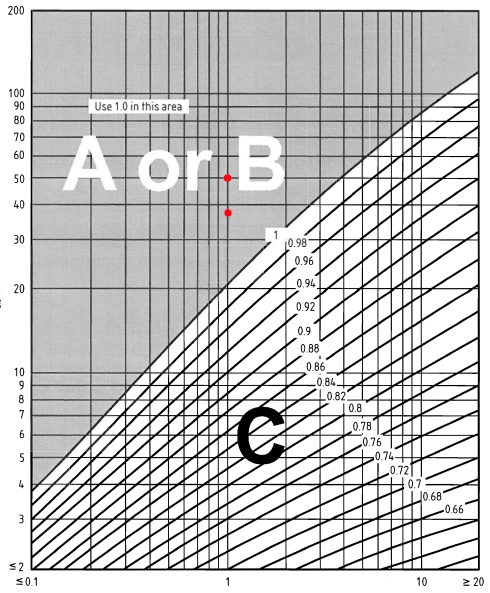
Φιγούρα 7. Εικόνα ΝΑ.8 του BS EN 1991-1-4 Εθνικό Παράρτημα.
Επομένως:
\({ντο}_{μι,Τ}(38.0) = 1.0\)
\({ντο}_{μι,Τ}(44.0) = 1.0\)
Χρησιμοποιώντας τις παραπάνω τιμές, μπορούμε να υπολογίσουμε την πίεση της μέγιστης ταχύτητας, \({ε}_{Π}(με)\), Για \(z = 38.0\) και \(z = 50.0\):
\({ε}_{Π}(44.0) = (3.3)(1.0)(353.09) = 1165.20 Καλά \)
\({ε}_{Π}(38.0) = (3.2)(1.0)(353.09) = 1129.89 Καλά \)
Δομικός Παράγοντας, \( {ντο}_{μικρό}{ντο}_{ρε} \)
Για την πινακίδα μας, θα χρησιμοποιήσουμε απλοποιημένη τιμή για τον δομικό παράγοντα, \({ντο}_{μικρό}{ντο}_{ρε}\), να είναι ίσο με 1.0 με βάση την Ενότητα 6 ή ΚΑΙ 1991-1-4.
Συντελεστής Δύναμης, \( {ντο}_{φά}\), για πινακίδα
Για πινακίδες, ο συντελεστής δύναμης, \({ντο}_{φά}\), είναι ίσο με 1.8 με βάση την Ενότητα 7.4.3 ή ΚΑΙ 1991-1-4.
Δύναμη του ανέμου, \( {φά}_{β,πινακίδα αγγελίας} \), ενεργώντας στην πινακίδα
Η δύναμη που ενεργεί στην πινακίδα μπορεί να υπολογιστεί χρησιμοποιώντας την Εξίσωση (7) με βάση την Ενότητα 5.3(2) ή ΚΑΙ 1991-1-4.
\({φά}_{β,πινακίδα αγγελίας} = {ντο}_{μικρό}{ντο}_{ρε}{ντο}_{φά}{ε}_{Π}({με}_{μι}){ΕΝΑ}_{αναφ,πινακίδα αγγελίας} = (1.0)(1.8)(1165.20Καλά)(12.0Μ)(12.0Μ)\)
\({φά}_{β,πινακίδα αγγελίας} = 302019.84 N)
Σημειώστε ότι η οριζόντια εκκεντρότητα αυτής της δύναμης ανέμου που ενεργεί στο κέντρο της πινακίδας συνιστάται να είναι ίση με 3,0 m.
Όλοι οι υπολογισμοί ανέμου μπορούν να εκτελεστούν χρησιμοποιώντας τη Γεννήτρια Φορτίου SkyCiv για EN 1991 (πινακίδα και αριθμομηχανή φορτίου ανέμου πόλου). Οι χρήστες μπορούν να εισαγάγουν την τοποθεσία του ιστότοπου για να λάβουν την ταχύτητα του ανέμου και τα δεδομένα του εδάφους, εισαγάγετε τις παραμέτρους του ηλιακού πάνελ και δημιουργήστε τις σχεδιαστικές πιέσεις ανέμου. Με την αυτόνομη έκδοση, μπορείτε να απλοποιήσετε αυτή τη διαδικασία και να λάβετε μια λεπτομερή αναφορά υπολογισμού φορτίου ανέμου για πινακίδες και στύλους!
Δύναμη του ανέμου, \( {φά}_{β,Πόλος} \), ενεργώντας στον στύλο
Ομοίως, Η δύναμη που επενεργεί στον πόλο μπορεί να υπολογιστεί χρησιμοποιώντας την Εξίσωση (7) με βάση την Ενότητα 5.3(2) ή ΚΑΙ 1991-1-4.
\({φά}_{β,Πόλος} = {ντο}_{μικρό}{ντο}_{ρε}{ντο}_{φά}{ε}_{Π}({με}_{σολ}){ΕΝΑ}_{αναφ,Πόλος}\) (8)
Οπου:
\({ντο}_{φά} = {ντο}_{φά,0}{ψ}_{λ} \)
\({ΕΝΑ}_{αναφ,Πόλος} = {με}_{σολ}ρε \)
Σημείωση:
\(ψ_{λ} \) υπολογίζεται με βάση την αποτελεσματική λεπτότητα, \( λ \), χρησιμοποιώντας τη χρήση του σχήματος 7.36 του τμήματος 7.13 ή ΚΑΙ 1991-1-4
\({ντο}_{φά,0}\) υπολογίζεται με βάση τον αριθμό Reynolds \( R_{μι} \) = Συντελεστής που εξηγεί τη μείωση της ταχύτητας με ύψος πάνω από το τοπικό έδαφος 7.28 ή ΚΑΙ 1991-1-4
Οπου:
\( {με}_{σολ} \) είναι το ύψος του στύλου από το έδαφος σε m
\( ρε \) είναι η διάμετρος του πόλου σε m
\( ν = 0.000015 τ.μ/δ \) είναι το κινηματικό ιξώδες του αέρα
\( β({με}_{σολ}) = (2{ε}_{Π}({με}_{σολ})/ρ)^{0.5} \) (9)
\( {Ρ}_{μι} = v(z_{σολ})d/ ν \) (10)
Θα βουτήξουμε βαθιά σε αυτές τις παραμέτρους στις επόμενες ενότητες
Αριθμός Reynolds, \( {Ρ}_{μι} \), για τον πόλο
Χρησιμοποιώντας τις παραπάνω υπολογισμένες τιμές, μπορούμε να υπολογίσουμε \( β({με}_{σολ}) \) χρησιμοποιώντας την εξίσωση (9):
\( β({με}_{σολ}) = (2{ε}_{Π}({με}_{σολ})/ρ)^{0.5} = (2(1129.89)/(1.226))^{0.5} \)
\( β({με}_{σολ}) = 42.93 Κυρία)
Επομένως, τον αριθμό Reynolds \( R_{μι} \) για τον πόλο, χρησιμοποιώντας την εξίσωση (10) είναι:
\( {Ρ}_{μι} = v({με}_{σολ})d/ ν = (42.93)(1.0)/(0.000015) \)
\( {Ρ}_{μι} = 2862000 \)
Συντελεστής δύναμης, \( {ντο}_{f0} \), χωρίς ροή ελεύθερου άκρου
Το υλικό πόλων που χρησιμοποιήσαμε είναι χυτοσίδηρος που έχει ισοδύναμη τραχύτητα επιφάνειας \( κ \) ίσο με 0.2 με βάση τον Πίνακα 7.13 ή ΚΑΙ 1991-1-4.
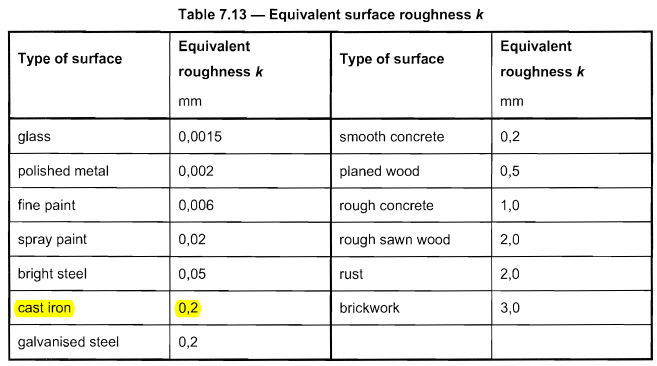
Φιγούρα 8. Τραπέζι 7.13 ή ΚΑΙ 1991-1-4 για ισοδύναμη τραχύτητα \( κ \).
Ο συντελεστής δύναμης \( {ντο}_{f0} \) μπορεί να προσδιοριστεί χρησιμοποιώντας τον τύπο από το σχήμα 7.28 του ΕΝ 1991-1-4 με \( k/d = 0.2\):
\( {ντο}_{f0}= 1.2 + {0.18κούτσουρο(10 κ/η)}/{1 + 0.4κούτσουρο({Ρ}_{μι}/{10}^{6}} = 1.2 + {0.18κούτσουρο(10 (0.2)}/{1 + 0.4κούτσουρο((2862000)/{10}^{6}}\)
\( {ντο}_{f0} = 1.246 \)
Αποτελεσματική Λεπτότητα, \( λ \)
Η αποτελεσματική λεπτότητα, \( λ \), για τον στύλο μπορεί να προσδιοριστεί από τον Πίνακα Νο.4 7.16 ή ΚΑΙ 1991-1-4.
\( λ = max(0.7 {με}_{σολ}/ρε, 70) \) Για \( {με}_{σολ} \) > 50Μ
\( λ = max({με}_{σολ}/ρε, 70) \) Για \( {με}_{σολ} \) < 15Μ
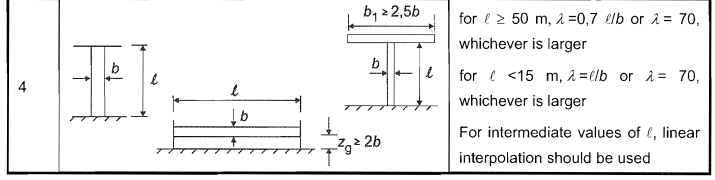
Φιγούρα 9. Τραπέζι 7.16 ή ΚΑΙ 1991-1-4 για τον υπολογισμό της Αποτελεσματικής Λεπτότητας \( λ \).
Από \( {με}_{σολ} \) ισούται με 38,0μ, πρέπει να παρεμβάλουμε τις τιμές του \( λ \) για 50μ και 15μ:
\( {με}_{σολ} = 38\)
\( {λ}_{50Μ} = μέγ(0.7 (38), 70) = 70 \)
\( {λ}_{15Μ} = μέγ((38), 70) = 70 \)
Επομένως:
\( λ = 70 \)
Παράγοντας τελικού αποτελέσματος, \( {ψ}_{λ} \)
Ο παράγοντας τελικού αποτελέσματος, \( {ψ}_{λ} \), μπορεί να ληφθεί χρησιμοποιώντας το σχήμα 7.36 ή ΚΑΙ 1991-1-4 που απαιτεί την αναλογία στερεότητας \( φ \) και αποτελεσματική λεπτότητα \( λ \). Θα υποθέσουμε λόγο στερεότητας \( φ \) ίσο με 1.0 αφού η στήλη του σωλήνα δεν έχει καμία διάτρηση.
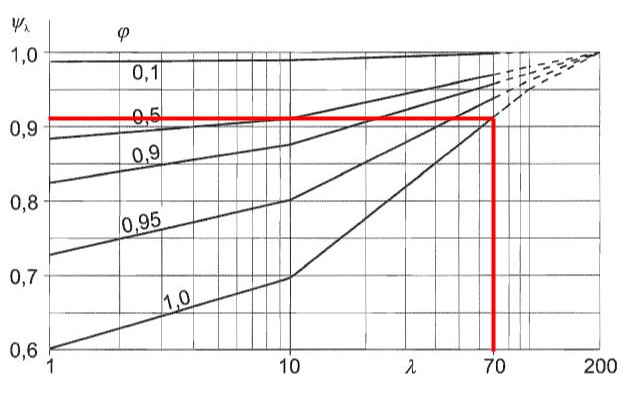
Φιγούρα 10. Ο αντίστοιχος παράγοντας τελικού αποτελέσματος \( {ψ}_{λ} \) για τον στύλο που στηρίζει την πινακίδα με βάση το Σχήμα 7.36 ή ΚΑΙ 1991-1-4.
Από το σχήμα 10, μπορούμε να συμπεράνουμε ότι ο παράγοντας τελικού αποτελέσματος \( {ψ}_{λ} \) γιατί ο πόλος ισούται με 0.910.
Από τις παραπάνω υπολογισμένες παραμέτρους,μπορούμε ήδη να υπολογίσουμε το Δύναμη του ανέμου, \( {φά}_{β,Πόλος} \):
\({ντο}_{φά} = {ντο}_{φά,0}{ψ}_{λ} = (1.246)(0.910) = 1.134\)
\({φά}_{β,Πόλος} = {ντο}_{μικρό}{ντο}_{ρε}{ντο}_{φά}{ε}_{Π}({με}_{μι}){ΕΝΑ}_{αναφ,Πόλος} = (1.0)(1.134)(1129.89)(38.0×1.0) \)
\({φά}_{β,Πόλος} = 48689.22 Ν \)
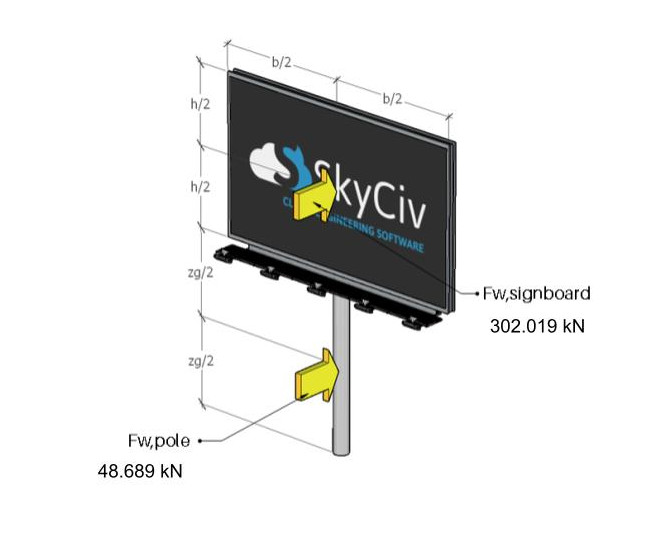
Φιγούρα 11. Οι δυνάμεις του ανέμου που δρουν στην πινακίδα και στον στύλο.
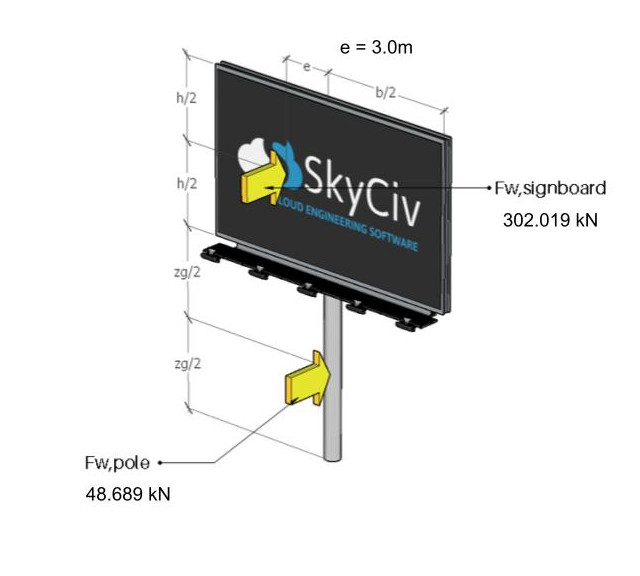
Φιγούρα 12. Οι δυνάμεις του ανέμου που ενεργούν στην πινακίδα και στον στύλο για έκκεντρη θήκη.
Γεννήτρια φορτίου SkyCiv
ποικίλλει ανάλογα με το υψόμετρο από το έδαφος του υπό εξέταση ύψους, μπορείτε να λάβετε φορτία ανέμου για πινακίδες και στύλους με λίγα μόνο κλικ και εισόδους. Όταν αγοράζετε την αυτόνομη έκδοση ή εγγραφείτε στον λογαριασμό Professional, θα μπορείτε να δημιουργήσετε τη λεπτομερή αναφορά ανέμου για το έργο πινακίδας σας!
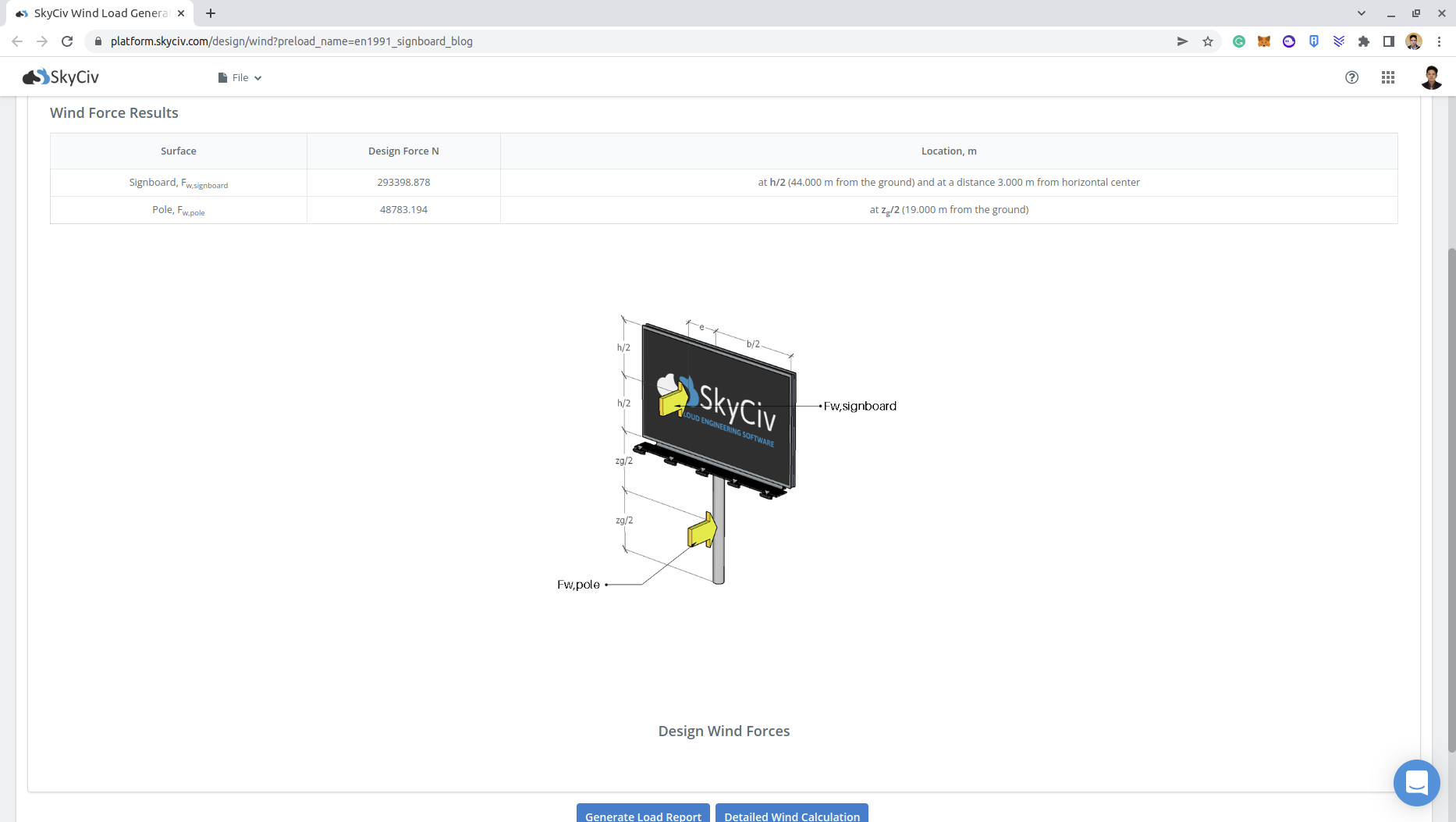
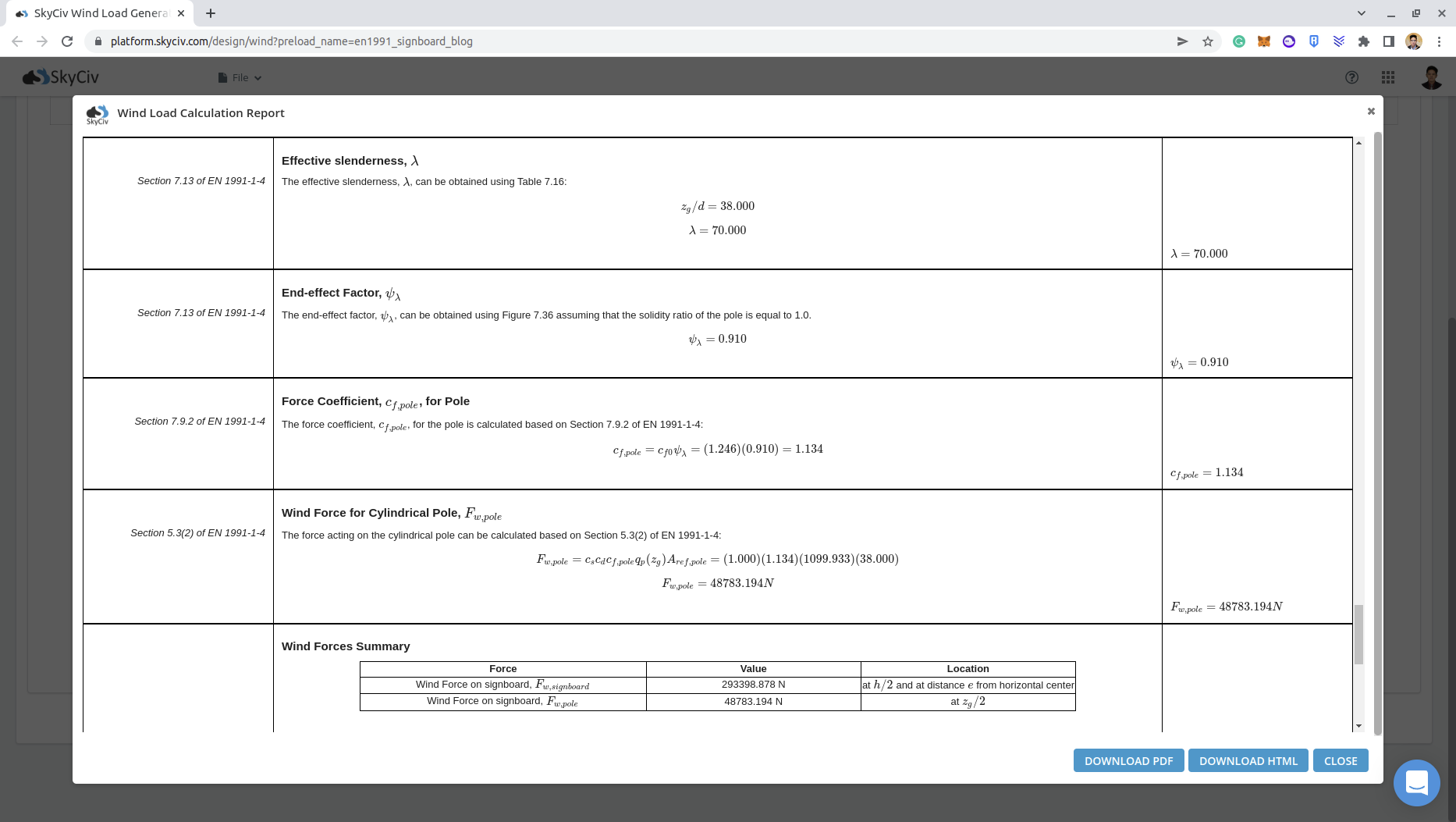
Μπορείτε να ελέγξετε τη λεπτομερή αναφορά φορτίου ανέμου για την πινακίδα μέσω αυτών των συνδέσμων:
Δομικός μηχανικός, Ανάπτυξη προϊόντων
MS Πολιτικών Μηχανικών
βιβλιογραφικές αναφορές:
- Σε, σι. (2005). Ευρωκώδικας 1: Δράσεις σε δομές — Μέρος 1–4: Γενικές δράσεις — Ενέργειες ανέμου.
- BSI. (2005). BS EN 1991-1-4: 2005+ Α'1: 2010: Ευρωκώδικας 1. Δράσεις σε δομές. Γενικές ενέργειες. συνδυάζοντας την επίδραση της εξωτερικής και εσωτερικής δράσης πίεσης.


