Μια περίληψη των υπολογισμών για το σχεδιασμό μιας απομονωμένης βάσης (ΟΠΩΣ ΚΑΙ 3600 2018)

Το θεμέλιο είναι ένα βασικό οικοδομικό σύστημα που μεταφέρει δυνάμεις υποστυλωμάτων και τοίχων στο έδαφος στήριξης. Ο μηχανικός μπορεί να επιλέξει ένα ρηχό ή βαθύ σύστημα θεμελίωσης με βάση τα χαρακτηριστικά του εδάφους και τα κτιριακά φορτία.

Ενότητα SkyCiv FoundationDesign includes analyzing and designing isolated footing conforming to the Australian Standards (ΟΠΩΣ ΚΑΙ 3600 2009 & 2018).

 

 

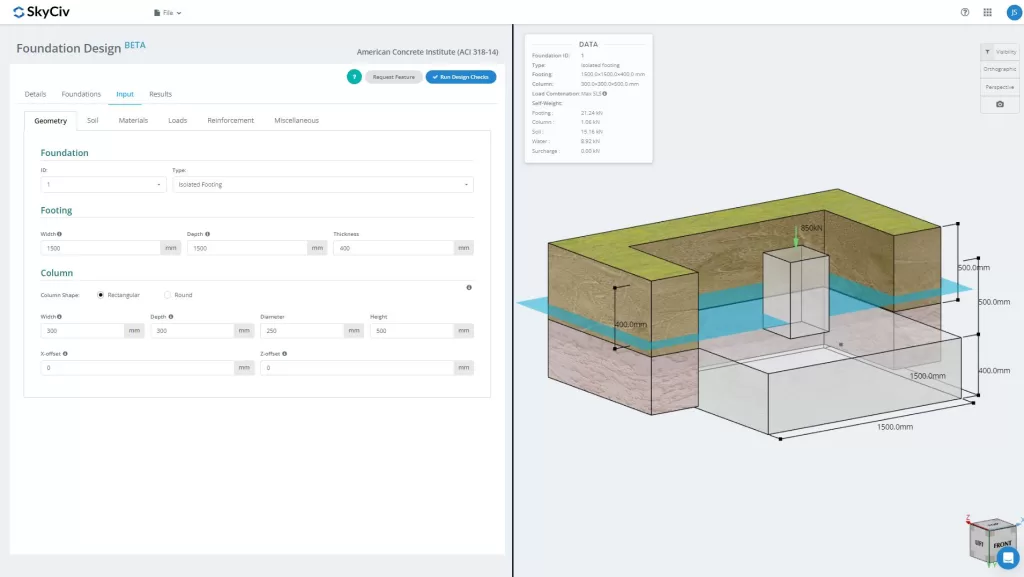
Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Our tool allows users to perform load-carrying calculations without any download or installation!

Υπολογιστής βάσης σκυροδέματος

Design of an Isolated Footing

---

Απαιτήσεις διάστασης

Για τον προσδιορισμό των διαστάσεων μιας απομονωμένης βάσης, σέρβις ή ατέλειωτα φορτία, such as permanent action (σολ), imposed action (Ερ), wind action (Δ_εσύ), earthquake action (μι_εσύ), και μικρό_εσύ will be applied using Load Combinations, as defined by AS 3600. Ό, τι κι αν συνδυάζει φορτίο θα θεωρείται το φορτίο σχεδιασμού, και συγκρίνεται με την επιτρεπόμενη πίεση εδάφους όπως φαίνεται στην Εξίσωση 1.

\(\κείμενο{ε}_{\κείμενο{ένα}} = frac{\κείμενο{Π}_{\κείμενο{ν}}}{\κείμενο{ΕΝΑ}} \δεξί βέλος \) Εξίσωση 1

ε_ένα = επιτρεπόμενη πίεση εδάφους
Π_ν = service level design loads
A = foundation area

Οι διαστάσεις του πέλματος μπορούν αρχικά να εκτιμηθούν λύνοντας την περιοχή θεμελίωσης (ΕΝΑ) χρησιμοποιώντας την εξίσωση 1.

\(\κείμενο{ΕΝΑ} = frac{\κείμενο{Π}_{\κείμενο{ν}}}{\κείμενο{ε}_{\κείμενο{ένα}}} \δεξί βέλος \) Εξίσωση 1α

Μονόδρομη κουρά

ο Διαδικτυακός υπολογιστής ποδιών για επιθέματα από σκυρόδεμα οριακή κατάσταση, γνωστός και ως κάμψη, αναγνωρίζει ότι η βάση μπορεί να αστοχήσει σε διάτμηση παρόμοια με μια ευρεία δοκό κατά μήκος ενός κρίσιμου διατμητικού επιπέδου που βρίσκεται σε απόσταση “ρε” από την όψη της στήλης (Φιγούρα 1), βασισμένο στο AS3600 Clause 8.2.7.1

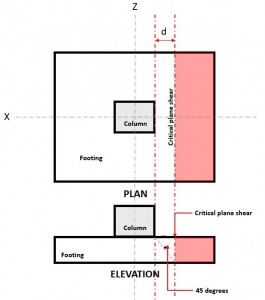
Φιγούρα 1. Critical Shear Plane of One-way Shear

ο Μονόδρομος Κουρεύω Ζήτηση ή Β_εσύ υπολογίζεται υποθέτοντας ότι το πέλμα είναι πρόβολο μακριά από τη στήλη όπου η κόκκινη περιοχή υποδεικνύεται στο σχήμα 1.

ο Μονόδρομος Κουρεύω Χωρητικότητα ή ϕVu_ντο ορίζεται ως η τελική διατμητική αντοχή και υπολογίζεται χρησιμοποιώντας την Εξίσωση 2 ανά AS3600-09 Cl 8.2.7.1.

\( \phi \text{Β}_{διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων} = \phi \beta_{1} \times \beta_{2} \times \beta_{3} \times b_{β} \times d_{ο} \φορές f_{cv} \φορές A_{αγ}^{\frac{2}{3}} \δεξί βέλος \) Εξίσωση 2 (AS3600 Eq. 8.2.7.1)

ϕ = shear design factor
β₁= 1.1(1.6 – ρε_ο/1000) ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi 1.1 ή 1.1(1.6(1-ρε_ο/1000) ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi 0.8
β₂ = 1, for members subject to pure bending; ή
=1-(Ν^*/3.5ΕΝΑ_σολ) ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi 0 for member subject to axial tension; ή
=1-(Ν^*/14ΕΝΑ_σολ) for members subject to axial compression
β₃ = 1, or may be taken as –
2ρε_ο/ένα_β αλλά όχι μεγαλύτερο από 2
ένα_β = distance for the section at which shear is being considered to the face of the nearest support
φά_cv = f’c^1/3 ≤ 4 MPa
ΕΝΑ_αγ = cross-sectional area of longitudinal reinforcement

Shear Demand and Shear Capacity must meet the following equation to meet the design requirements of AS 3600-09:

\(\κείμενο{Β}_{\κείμενο{εσύ}} \leq phi κείμενο{Β}_{\κείμενο{διευκρινίζει ότι οι πασσάλοι απαιτείται να έχουν ανοχή εκτός θέσης 75 mm για την οριζόντια τοποθέτηση των πασσάλων}} \δεξί βέλος \) Εξίσωση 3 (ανά AS3600 Cl. 8.2.5)

Ίδρυμα SkyCiv, σε συμμόρφωση με την Εξίσωση 3, υπολογίζει τον λόγο χρησιμότητας μονής διάτμησης (Εξίσωση 4) λαμβάνοντας το Shear Demand πάνω από το Shear Capacity.

\( \κείμενο{Αναλογία χρησιμότητας} = frac{\κείμενο{Διατμητική ζήτηση}}{\κείμενο{Ικανότητα διάτμησης}} \δεξί βέλος \) Εξίσωση 4

Αμφίδρομη κουρά

ο Αμφίδρομη κουρά οριακή κατάσταση, γνωστός και ως διάτμηση διάτμησης, επεκτείνει το κρίσιμο τμήμα του σε απόσταση “δ/2” από την όψη της στήλης και περιμετρικά της στήλης (Φιγούρα 2) βασισμένο στο AS3600 Clause 9.2.3(ένα).

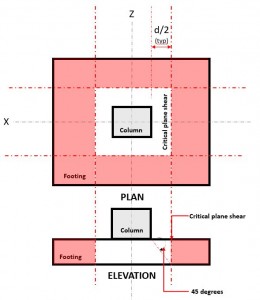
Φιγούρα 2. Κρίσιμο επίπεδο διάτμησης αμφίδρομης διάτμησης

ο Δύο τρόποιάκου Ζήτηση ή Β_εσύ εμφανίζεται στο κρίσιμο επίπεδο διάτμησης, που βρίσκεται σε απόσταση από “δ/2” όπου το (το κόκκινο) εκκολαφθείσα περιοχή, as indicated in Figure 2.

ο Αμφίδρομη Ικανότητα διάτμησης ή ϕV_{Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού} ορίζεται ως η τελική διατμητική αντοχή και υπολογίζεται χρησιμοποιώντας την Εξίσωση 5 βασισμένο στο AS3600 Clause 9.2.3

\( \phi V_{Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού} = \phi \times u \times f_{cv} \times d \rightarrow \) Εξίσωση 5 (AS3600 Cl. 9.2.3(ένα))

φά_cv = 0.17(1 + 2/β_η) √f’_ντο ≤ 0.34√f’_ντο
β_η = ratio of the length of the column at the Z-axis over the X-axis

d = απόσταση από ακραίες ίνες συμπίεσης έως κεντροειδές οπλισμό διαμήκους τάσης (χιλ)
u = length of the critical shear perimeter (χιλ)

Shear Demand and Shear Capacity must meet the following equation to meet the design requirements of AS 3600:

\(\κείμενο{Β}_{\κείμενο{εσύ}} \leq phi κείμενο{Β}_{\κείμενο{Η δομική αντοχή σχεδιασμού ενός πασσάλου σκυροδέματος είναι ισοδύναμη με την τελική αντοχή σχεδιασμού}} \δεξί βέλος \) Εξίσωση 6 (ανά AS3600 Cl. 8.2.5)

Ίδρυμα SkyCiv, σε συμμόρφωση με την Εξίσωση 6, calculates the two-way shear utility ratio (Εξίσωση 7) λαμβάνοντας το Shear Demand πάνω από το Shear Capacity.

\( \κείμενο{Αναλογία χρησιμότητας} = frac{\κείμενο{Διατμητική ζήτηση}}{\κείμενο{Ικανότητα διάτμησης}} \δεξί βέλος \) Εξίσωση 7

Κάμψη

In an isolated footing, Οι λεπτομερείς αναφορές αντικατοπτρίζουν συνδυασμούς φορτίου. Bending moments are calculated in each direction at section 0.7ένα_γουλιά distance from the center of the column, όπου ένα_γουλιά Οι ροπές κάμψης υπολογίζονται σε κάθε κατεύθυνση σε τμήματα.

 

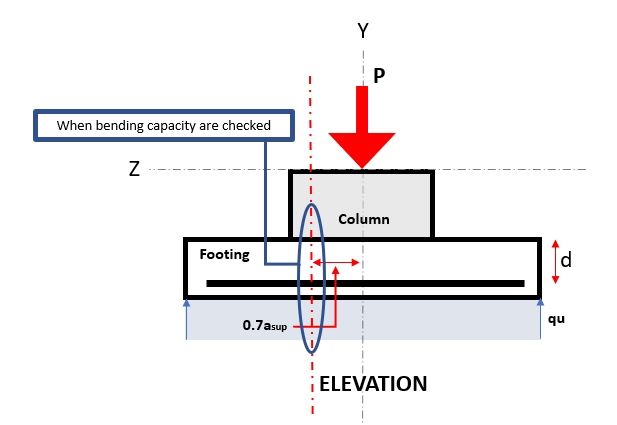
Φιγούρα 3. Τμήμα Κρίσιμης Κάμψης

ο Κάμψη limit state occurs at the Critical Flexure Section, located 0.7ένα_γουλιά from the center of the footing (Ανατρέξτε στην Εικόνα 3).

ο Καμπλαστική ζήτηση ή Μ_εσύ is located at the Critical Flexure Section indicated in Figure 3, και υπολογίζεται χρησιμοποιώντας την εξίσωση 8.

\( \κείμενο{Μ}^{*}= q_{εσύ} \times D_{φά} \φορές αριστερά( \frac{ \frac{αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{φά} – αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ντο}}{2} }{2} \σωστά)^{2} \δεξί βέλος \) Εξίσωση 8

Πρόσθετες επαληθεύσεις

Άλλες επαληθεύσεις που δεν αναφέρονται στον κωδικό, συμπεριλαμβανομένων των ελέγχων πίεσης εδάφους, ανύψωση, και άλλοι έλεγχοι σταθερότητας επαληθεύονται επίσης.

Διπλή διάτμηση

Ο προσδιορισμός της βασικής πίεσης ή η αλληλεπίδραση μεταξύ εδάφους και βάσης βασίζεται κυρίως στις διαστάσεις του πέλματος και στην προκύπτουσα εκκεντρότητα των εφαρμοζόμενων φορτίων. Ανάλογα με την τοποθέτηση αυτής της προκύπτουσας εκκεντρότητας, η πίεση βάσης μπορεί να προκαλέσει πλήρη ή μερική συμπίεση στο πέλμα. Αυτή η αξιολόγηση μας δίνει τη δυνατότητα να επιβεβαιώσουμε εάν το υποκείμενο έδαφος μπορεί να αντέξει το σύνολο των φορτίων που μεταδίδονται από το πέλμα.

Για έναν λεπτομερή οδηγό για τον χειροκίνητο υπολογισμό της πίεσης του εδάφους, ανατρέξτε σε αυτόν τον σύνδεσμο: Κατανομή πίεσης κάτω από ορθογώνιο πέλμα από σκυρόδεμα

Ο λόγος χρησιμότητας αξιολογείται συγκρίνοντας τη μέγιστη πίεση του εδάφους (κατάσταση λειτουργικότητας) με την επιτρεπόμενη μικτή φέρουσα ικανότητα εδάφους:

 

\( \κείμενο{Αναλογία χρησιμότητας} = frac{\κείμενο{Μέγιστη. Διπλή διάτμηση}}{\κείμενο{Ακαθάριστη Επιτρεπόμενη Χωρητικότητα Εδάφους}} \δεξί βέλος \) Εξίσωση 14

Ανύψωση

Ελέγχει το ρυθμιζόμενο αξονικό φορτίο που επενεργεί στο πέλμα. Αθροίζει όλα τα κατακόρυφα φορτία, συμπεριλαμβανομένου του φορτίου χρήστη και των αυτο-σταθμίσεων της στήλης, πλάκα βάσης, έδαφος, και άνωσης δύναμης. Αν η στήλη δεχτεί ανοδική δύναμη, τα αυτο-βαρίδια που καθορίζονται πρέπει να αντισταθμίζουν την ανοδική δύναμη; σε διαφορετική περίπτωση, ο σχεδιασμός κινδυνεύει να αποτύχει λόγω αστάθειας.

Ανατροπή

Η ανατροπή του πέλματος ελέγχεται αθροίζοντας όλες τις στιγμές γύρω από ένα σημείο του πέλματος συμπεριλαμβανομένων όλων των δυνάμεων που ασκούνται σε αυτό. Όλοι οι συνδυασμοί φορτίου λειτουργικότητας πρέπει να λαμβάνονται υπόψη για τον έλεγχο της ροπής ανατροπής που διέπει. Συνήθως, ένας παράγοντας ασφάλειας του 1.5-2 χρησιμοποιείται για να αξιολογήσει εάν το στήριγμα περνά τον έλεγχο ανατροπής.

Ολίσθηση

Για έλεγχο για ολίσθηση, το άθροισμα των οριζόντιων φορτίων αντίστασης που δείχνουν προς τα δεξιά διαιρείται με το άθροισμα των φορτίων που δείχνουν προς τα αριστερά.

• Αντοχή σε φορτία:
  • Οριζόντια δύναμη λόγω τριβής μεταξύ της βάσης του πέλματος και του εδάφους της υποδομής
  • Παθητική πίεση εδάφους (εάν περιλαμβάνονται)
• Συρόμενα φορτία:
  • Η οριζόντια συνιστώσα της ενεργού πίεσης του εδάφους
  • Η οριζόντια συνιστώσα της πίεσης που προκύπτει από την προσαύξηση

Γενικά, ένας ελάχιστος συντελεστής ασφάλειας του 1.5 χρησιμοποιείται. Εάν δεν ασκείται οριζόντια δύναμη στο πέλμα, δεν απαιτείται έλεγχος για ολίσθηση.

Ενότητα σχεδίασης του ιδρύματος SkyCiv

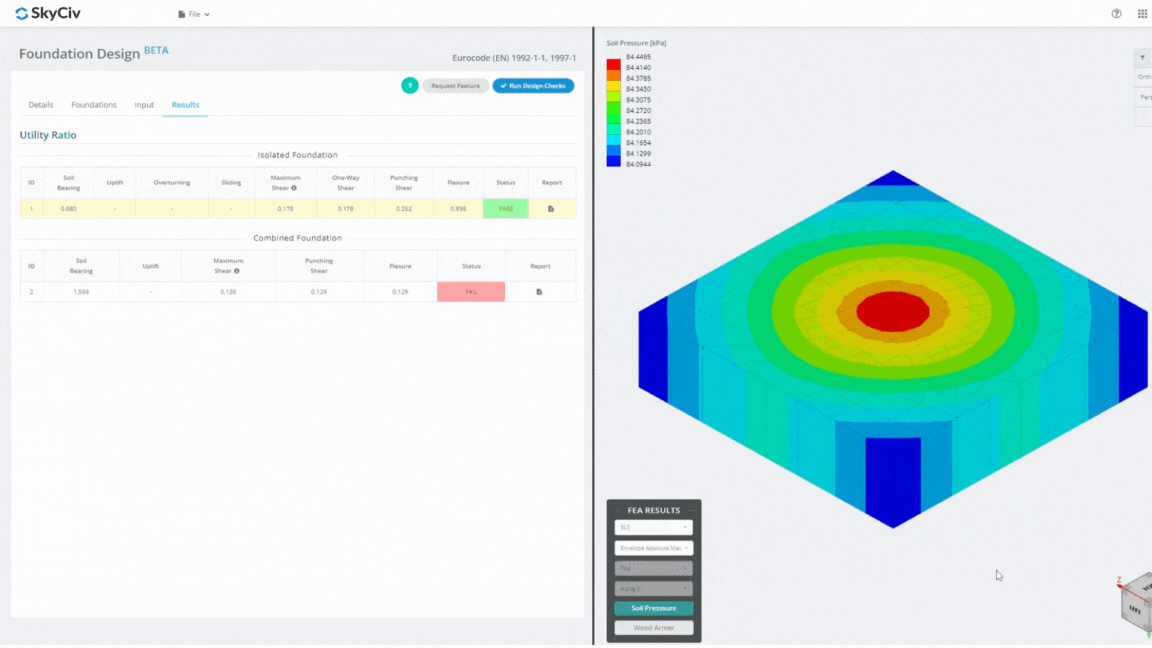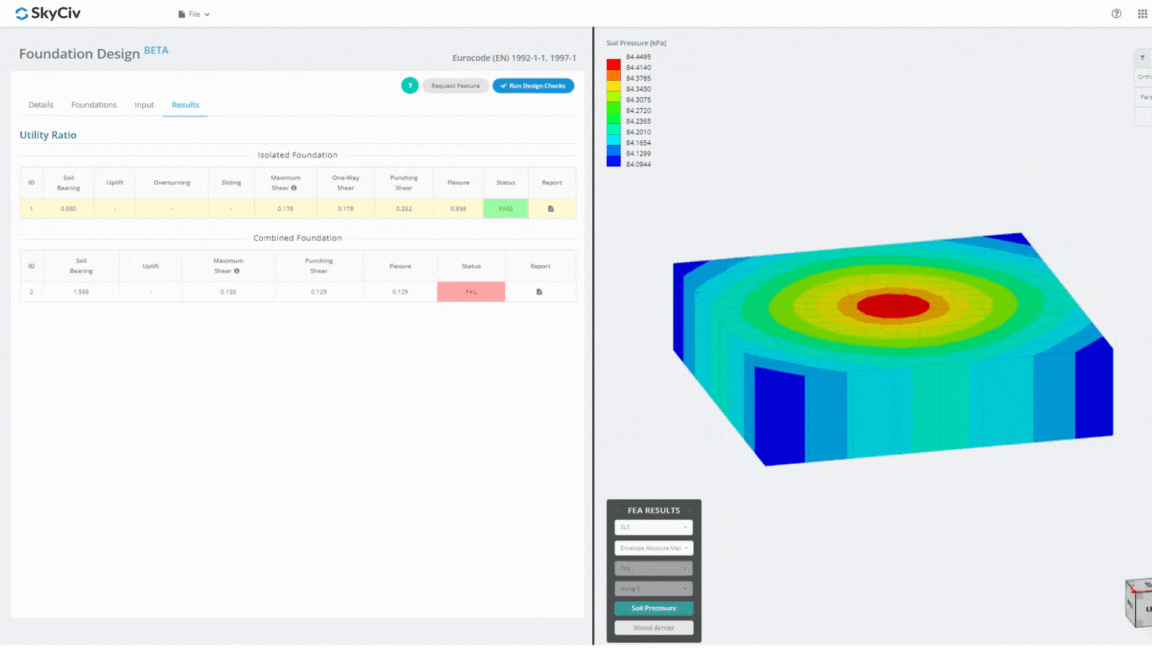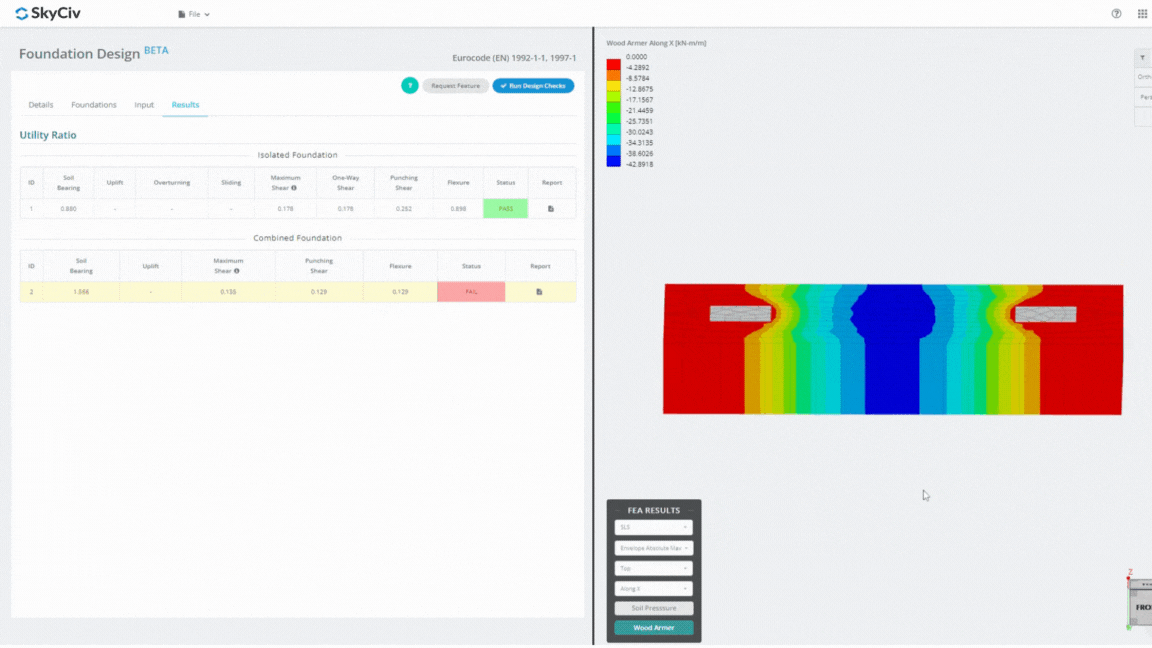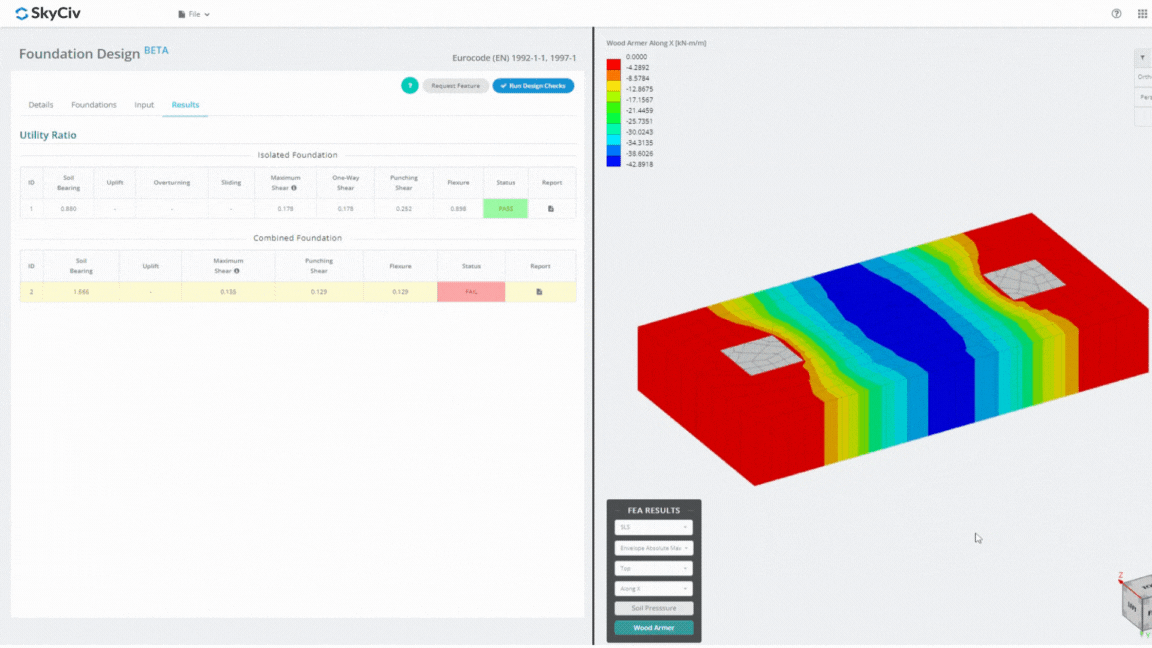
Το Foundation Design Module είναι ένα ισχυρό εργαλείο ενσωματωμένο με την ανάλυση πεπερασμένων στοιχείων (ΑΣΧΗΜΟΣ), ικανό να διεξάγει ενδελεχείς αναλύσεις πίεσης εδάφους και ξύλινου βραχίονα για λεπτομερείς ελέγχους κάμψης. Εκτελεί όλους τους δομικούς ελέγχους που καθορίζονται από την ACI 318 και άλλες επαληθεύσεις που αναφέρονται παραπάνω και τις παρουσιάζει σε ολοκληρωμένη αναφορά.

Ξεκινήστε με το SkyCiv Foundation σήμερα!

Εκκινήστε το Σχεδιασμός ιδρύματος και δοκιμάστε το σήμερα! Είναι εύκολο να ξεκινήσετε, αλλά αν χρειάζεστε περισσότερη βοήθεια, τότε φροντίστε να επισκεφθείτε μας τεκμηρίωση ή επικοινωνήστε μαζί μας!

Δεν είναι χρήστης SkyCiv? Εγγραφείτε για ένα Ελεύθερος 14 Ημέρα δοκιμής για να ξεκινήσετε!

βιβλιογραφικές αναφορές

1. Council of Standards Australia. (2009) Australian Standard AS3600-2009.
2. SJ Foster, AE Kilpatrick & RF Warner. (2011) Reinforced Concrete Basics 2nd Edition.
3. Τέιλορ, Ανδρέας, et αϊ. Εγχειρίδιο ενισχυμένου σκυροδέματος: ένας σύντροφος στο ACI-318-14. Αμερικανικό Ινστιτούτο Σκυροδέματος, 2015.
4. YC Loo & SH Chowdhury. (2013) Ενισχυμένος & Προεντεταμένο σκυρόδεμα.