1. Ορισμός εκτροπής δοκού
2. Μονάδα εκτροπής δοκού
3. Εξισώσεις παραμόρφωσης δέσμης/τύποι
   • Εξισώσεις εκτροπής Cantilever
   • Απλά υποστηριζόμενες εξισώσεις εκτροπής
   • Διορθώθηκαν εξισώσεις απόκλισης δέσμης
4. Παράδειγμα υπολογισμού παραμόρφωσης δέσμης με απλά υποστήριξη

 

1. Ορισμός εκτροπής δοκού

Τι είναι η εκτροπή? Εκτροπή, με όρους δομικής μηχανικής, αναφέρεται στην κίνηση μιας δέσμης ή κόμβου από την αρχική του θέση λόγω των δυνάμεων και των φορτίων που εφαρμόζονται στο μέλος. Είναι επίσης γνωστό ως μετατόπιση και μπορεί να προκύψει από εξωτερικά εφαρμοζόμενα φορτία ή από το βάρος της ίδιας της κατασκευής, και τη δύναμη της βαρύτητας στην οποία ισχύει αυτό.

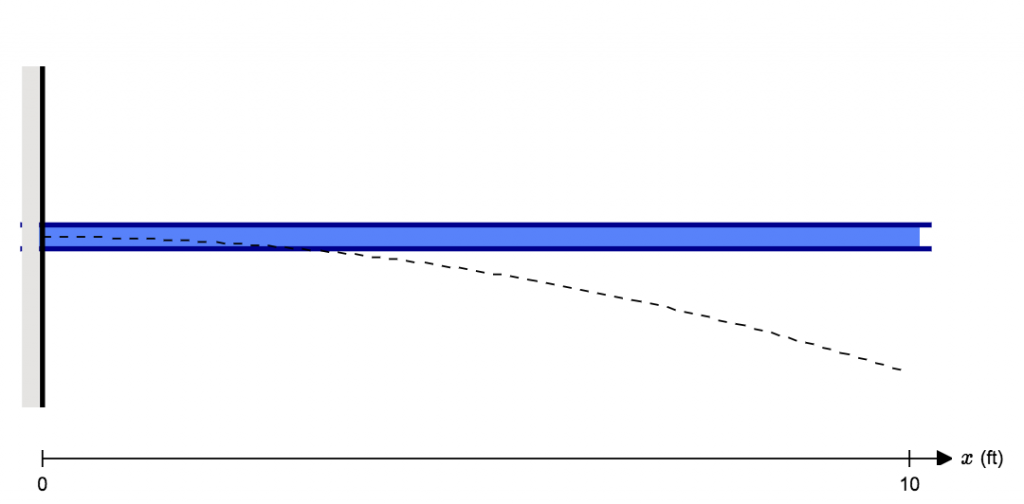
Η παραμόρφωση μπορεί να συμβεί σε δοκούς, δοκάρια, κουφώματα, και βασικά οποιαδήποτε άλλη δομή. Για να ορίσετε την εκτροπή, ας πάρουμε ένα απλό παραμόρφωση δοκού με πρόβολο που έχει ένα άτομο με βάρος (Δ) στέκεται στο τέλος:

Η δύναμη αυτού του ατόμου που στέκεται στο τέλος θα αναγκάσει τη δέσμη να λυγίσει και να εκτραπεί από τη φυσική της θέση. Στο παρακάτω διάγραμμα, η μπλε δέσμη είναι η αρχική θέση, και η διακεκομμένη γραμμή προσομοιώνει την εκτροπή δέσμης προβόλου:

Οπως βλέπεις, η δέσμη έχει λυγίσει ή απομακρυνθεί από την αρχική θέση. Αυτή η απόσταση σε κάθε σημείο κατά μήκος του μέλους είναι η έννοια ή ο ορισμός της εκτροπής.

Υπάρχουν γενικά 4 κύριες μεταβλητές που καθορίζουν πόσες παραμορφώσεις δέσμης. Αυτά περιλαμβάνουν:

• Πόση φόρτωση είναι στη δομή
• Το μήκος του μη υποστηριζόμενου μέλους
• Το υλικό, συγκεκριμένα το Young's Modulus
• Το μέγεθος διατομής, συγκεκριμένα τη στιγμή της αδράνειας (Εγώ)

 

2. Μονάδα εκτροπής δοκού

Η μονάδα εκτροπής, ή μετατόπιση, είναι μονάδα μήκους και συνήθως λαμβάνεται ως mm (για μέτρηση) και στο (για αυτοκρατορικό). Αυτός ο αριθμός καθορίζει την απόσταση στην οποία η δέσμη έχει εκτρέψει από την αρχική θέση. Δεδομένου ότι η εκτροπή είναι μια μέτρηση μικρής απόστασης (Οι δοκοί πρέπει γενικά να εκτρέπονται μόνο κατά μικρές ποσότητες), εκφράζεται συνήθως σε μονάδες μήκους, όπως ίντσες ή χιλιοστά.

Επιπροσθέτως, Υπάρχουν και άλλες παράμετροι που χρησιμοποιούνται για τη μέτρηση της παραμόρφωσης, όπως οι γωνίες, αλλά αυτές οι μονάδες όπως τα ακτίνια ή οι μοίρες δεν χρησιμοποιούνται συνήθως. Επιπροσθέτως, είναι σημαντικό να σημειωθεί ότι η επιτρεπόμενη απόκλιση για μια κατασκευή καθορίζεται συχνά ως ποσοστό του μήκους του ανοίγματος (L/X), Αυτό είναι ένα μέτρο που επιτρέπει τη σύγκριση μεταξύ διαφορετικών δοκών ανεξάρτητα από το μήκος τους και χωρίς μονάδα.

 

3. Εξισώσεις παραμόρφωσης δέσμης/τύποι

Οι εξισώσεις Beam Deflection είναι εύκολο να εφαρμοστούν και επιτρέπουν στους μηχανικούς να κάνουν απλούς και γρήγορους υπολογισμούς για εκτροπή. Εάν δεν είστε σίγουροι για το τι είναι πραγματικά η παραμόρφωση, κάντε κλικ εδώ για ένα ορισμός εκτροπής Ακολουθεί ένας συνοπτικός πίνακας εκτροπής δέσμης που δείχνει πώς να υπολογίσετε τη μέγιστη απόκλιση σε μια δέσμη. Δεν θέλετε να υπολογίσετε αυτά τα χέρια? Το SkyCiv προσφέρει δωρεάν αριθμομηχανή εκτροπής δέσμης για να βοηθήσετε στις ανάγκες σας! Για πιο ισχυρό λογισμικό δομικής ανάλυσης, εγγραφείτε για έναν δωρεάν λογαριασμό SkyCiv και αποκτήστε άμεση πρόσβαση σε όλες τις δωρεάν εκδόσεις του λογισμικό δομικής ανάλυσης cloud!

Χρησιμοποιήστε τον παρακάτω τύπο εκτροπής δέσμης για να υπολογίσετε τη μέγιστη μετατόπιση σε δοκούς. Κάντε κλικ στο κουμπί «έλεγχος απάντησης» για να ανοίξετε το δωρεάν μας αριθμομηχανή δέσμης. Αυτές οι εξισώσεις μετατόπισης δέσμης είναι ιδανικές για γρήγορους υπολογισμούς χεριών και γρήγορους σχεδιασμούς. Βρείτε αυτό που ψάχνετε πιο γρήγορα:

• Εξισώσεις εκτροπής Cantilever
• Απλά υποστηριζόμενες εξισώσεις εκτροπής
• Διορθώθηκαν εξισώσεις απόκλισης δέσμης

Η εκτροπή μιας δέσμης (εκτροπή δέσμης) υπολογίζεται με βάση διάφορους παράγοντες, συμπεριλαμβανομένων υλικών, τη στιγμή της αδράνειας ενός τμήματος, η δύναμη που εφαρμόζεται, και την απόσταση από την υποστήριξη. Αυτά μπορούν να απλοποιηθούν σε απλή φόρμουλα εκτροπής για γρήγορους υπολογισμούς στο πίσω μέρος του φακέλου. Ακολουθεί ένας απλός πίνακας των διαφορετικών σεναρίων φόρτωσης και των αντίστοιχων εξισώσεων μέγιστης παραμόρφωσης δέσμης:

 

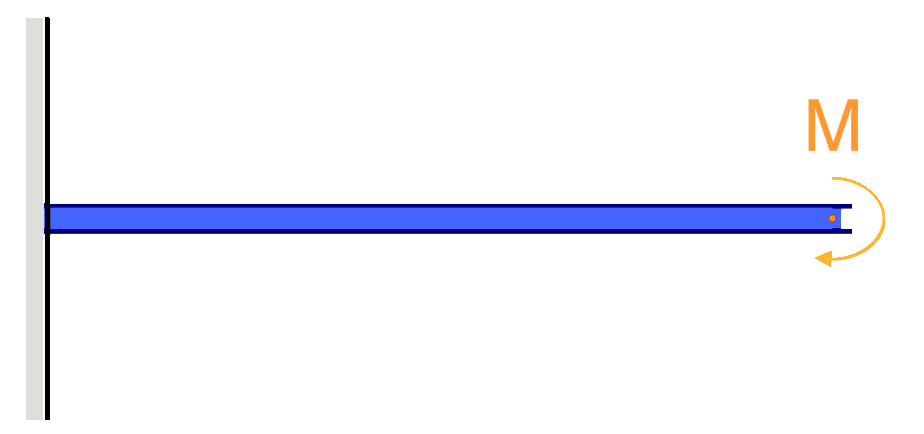
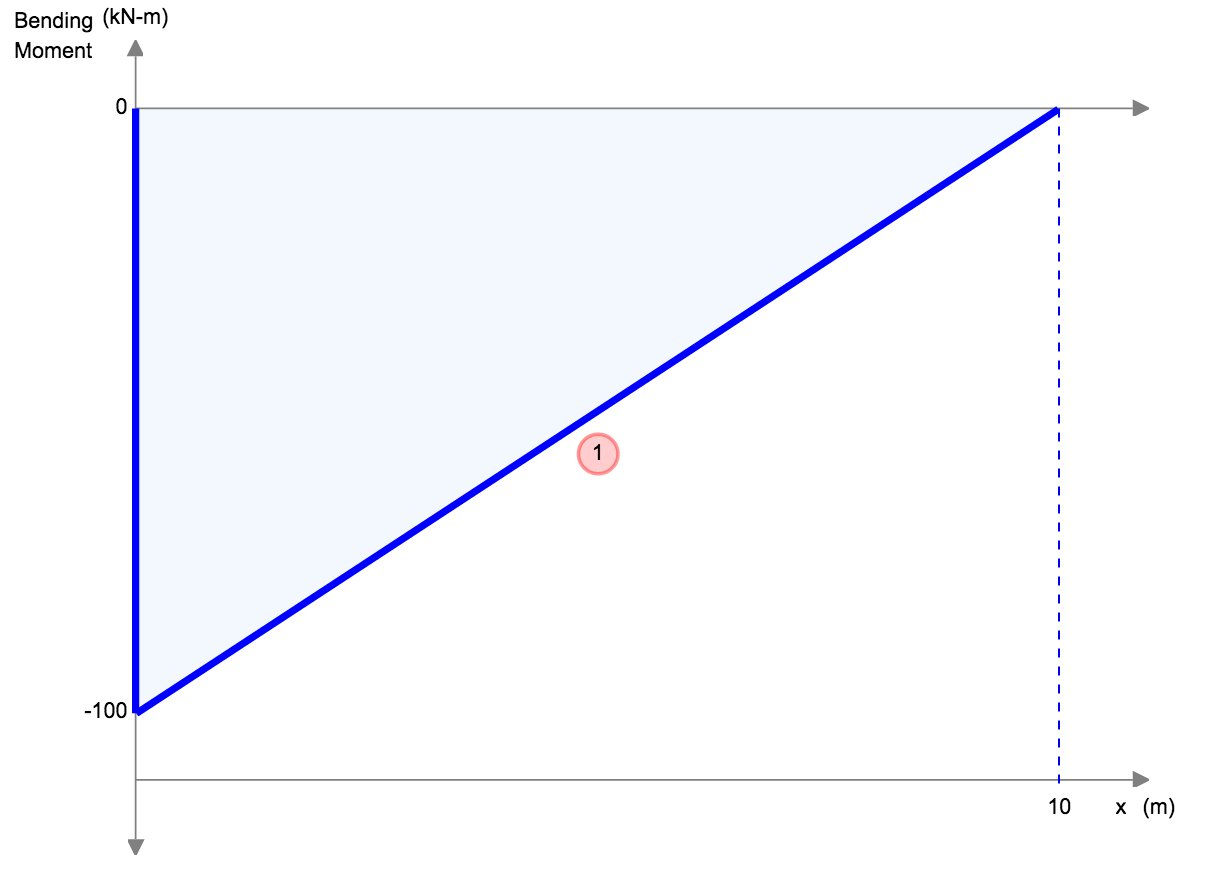
Εξισώσεις/Τύπες εκτροπής δοκού προβόλου

Οι δοκοί Cantilever είναι ειδικοί τύποι δοκών που περιορίζονται από μία μόνο υποστήριξη, όπως φαίνεται στο παραπάνω παράδειγμα. Αυτά τα μέλη φυσικά θα εκτρέψουν περισσότερο καθώς υποστηρίζονται μόνο στο ένα άκρο.

Είναι σημαντικό να ληφθεί υπόψη ότι η εκτροπή μιας δοκού προβόλου επηρεάζεται επίσης από τη θέση του φορτίου και τη θέση του σταθερού στηρίγματος. Όσο πιο μακριά είναι το φορτίο από το σταθερό στήριγμα, τόσο μεγαλύτερη θα είναι η απόκλιση. Και επίσης, όσο μεγαλύτερος είναι ο πρόβολος τόσο μεγαλύτερη θα είναι η απόκλιση, λόγω του γεγονότος ότι το φορτίο εφαρμόζεται σε μεγαλύτερη απόσταση.

Είναι επίσης σημαντικό να σημειωθεί ότι υπάρχει μια μέγιστη επιτρεπόμενη απόκλιση για κατασκευές, Αυτή η τιμή καθορίζεται συνήθως από οικοδομικούς κώδικες και πρότυπα, ποικίλλει ανάλογα με τον τύπο της δομής και το σκοπό της δομής, και η υπολογιζόμενη παραμόρφωση θα πρέπει να είναι εντός αυτού του ορίου για να διασφαλιστεί η ασφάλεια και η λειτουργικότητα της κατασκευής.

 

Αναφορά	Μέγιστη απόκλιση	Σχήμα BMD

 

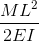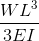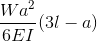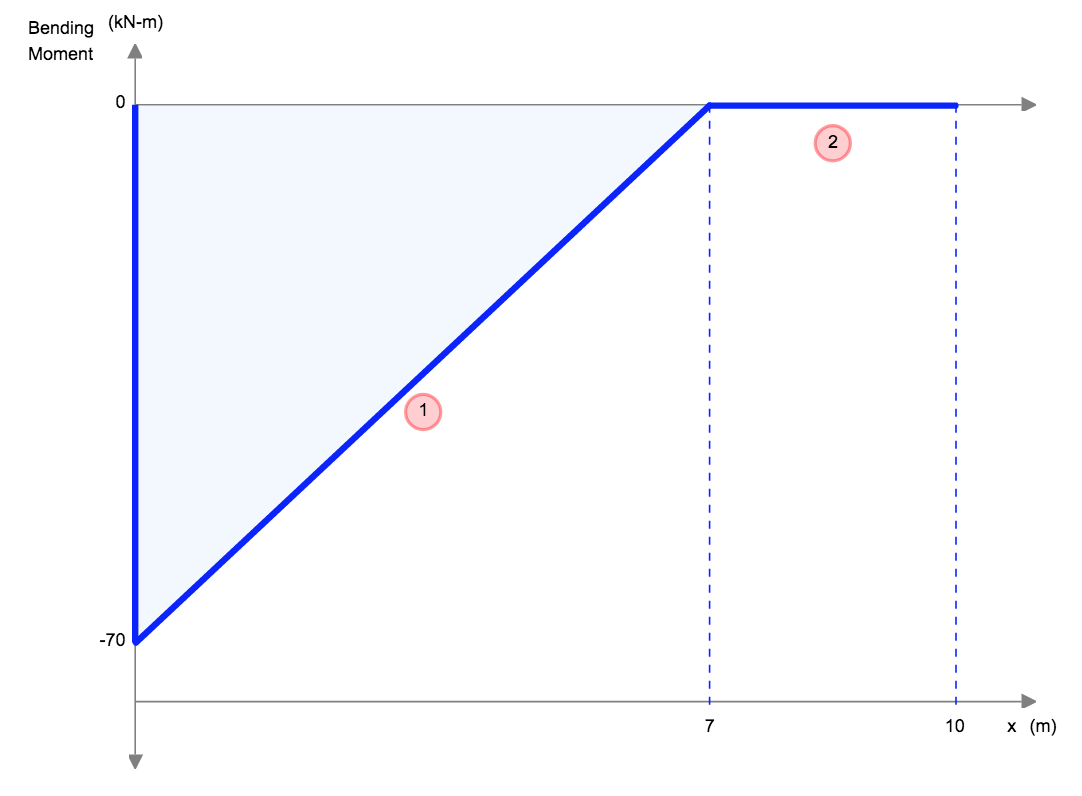Απλώς υποστηριζόμενες εξισώσεις/τύποι εκτροπής δέσμης

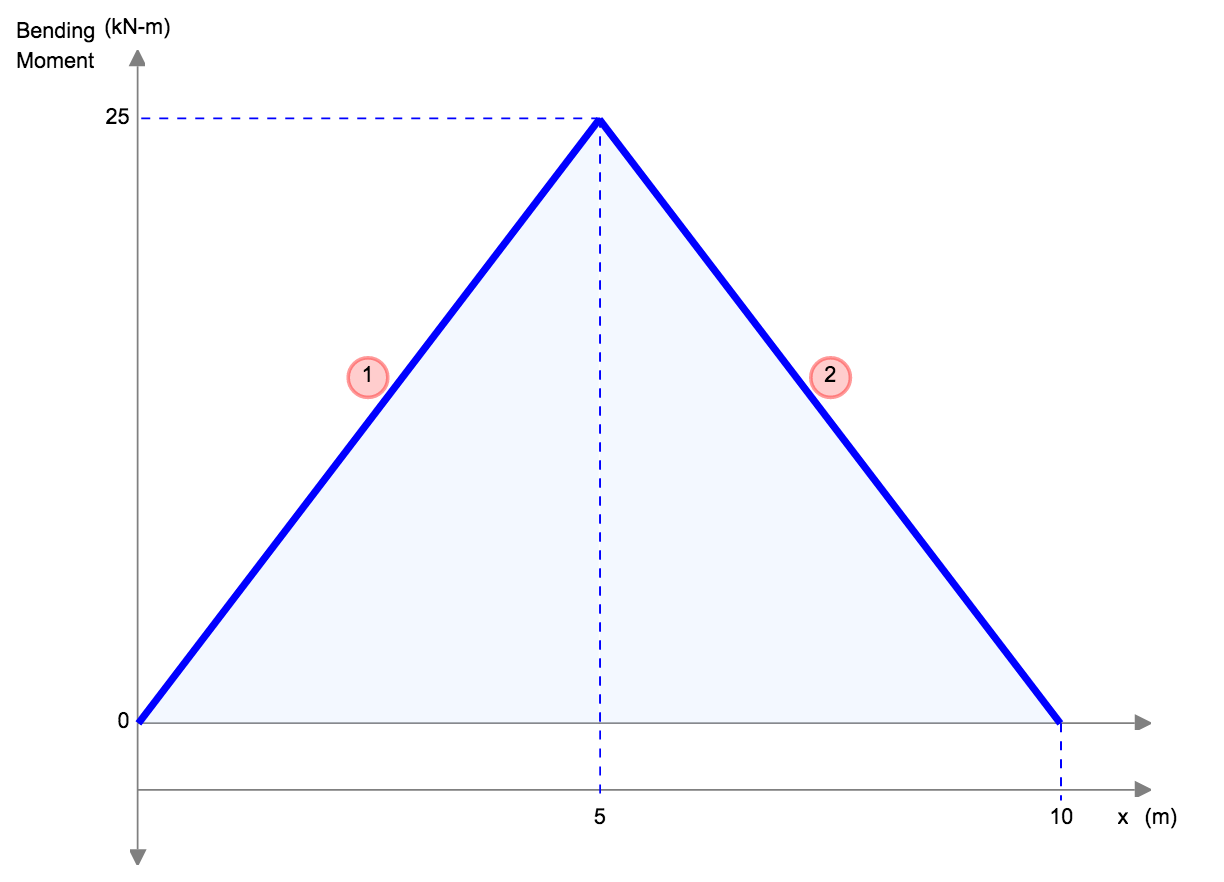
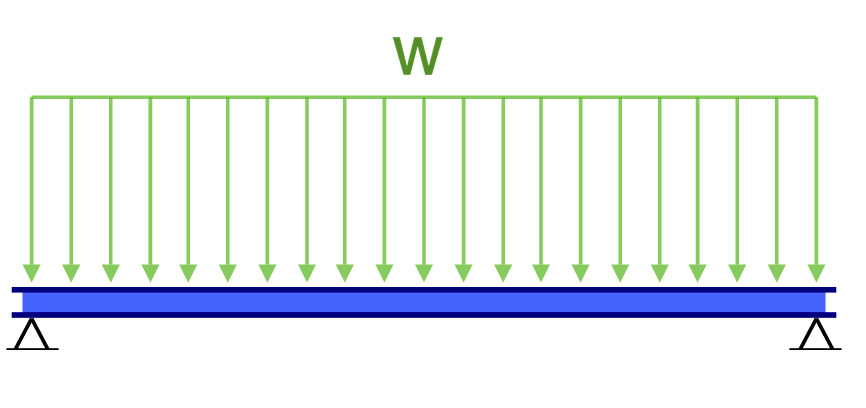
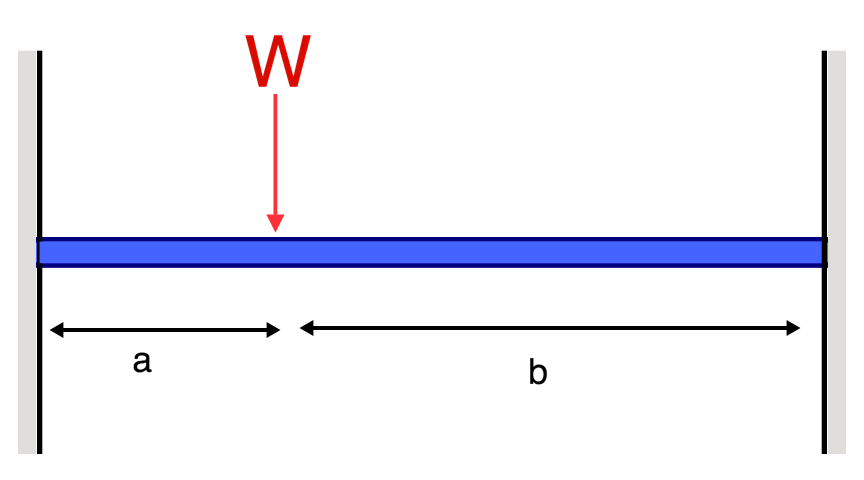
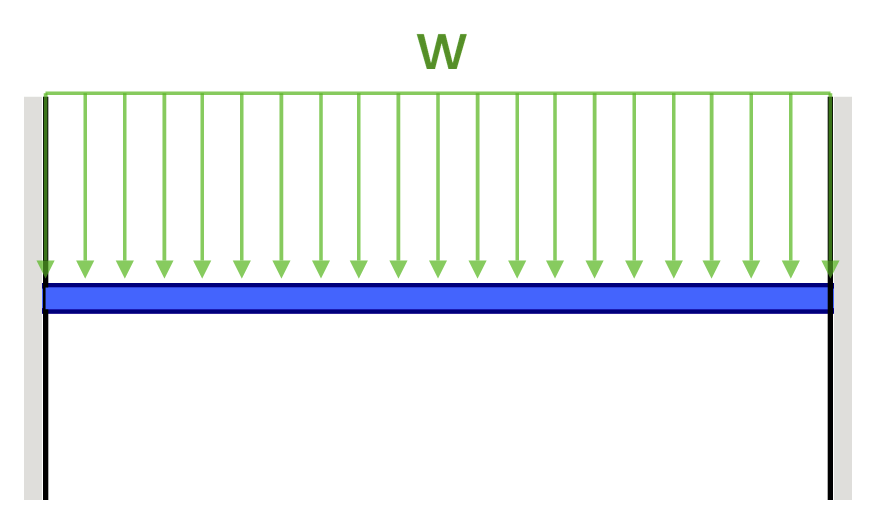
Ένα άλλο παράδειγμα εκτροπής είναι η εκτροπή μιας απλώς υποστηριζόμενης δέσμης. Αυτές οι δοκοί υποστηρίζονται και στα δύο άκρα, έτσι η εκτροπή μιας δοκού γενικά αφήνεται και ακολουθεί πολύ διαφορετικό σχήμα από αυτό του προβόλου. Κάτω από ένα ομοιόμορφο κατανεμημένο φορτίο (για παράδειγμα το αυτο-βάρος), η δέσμη θα εκτρέπεται ομαλά και προς το μέσο σημείο.

 

Αναφορά	Μέγιστη απόκλιση	Σχήμα BMD

 

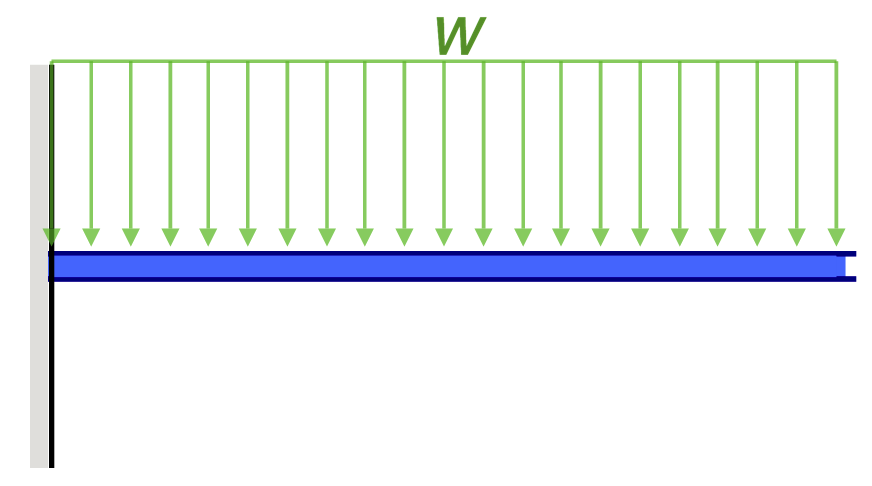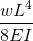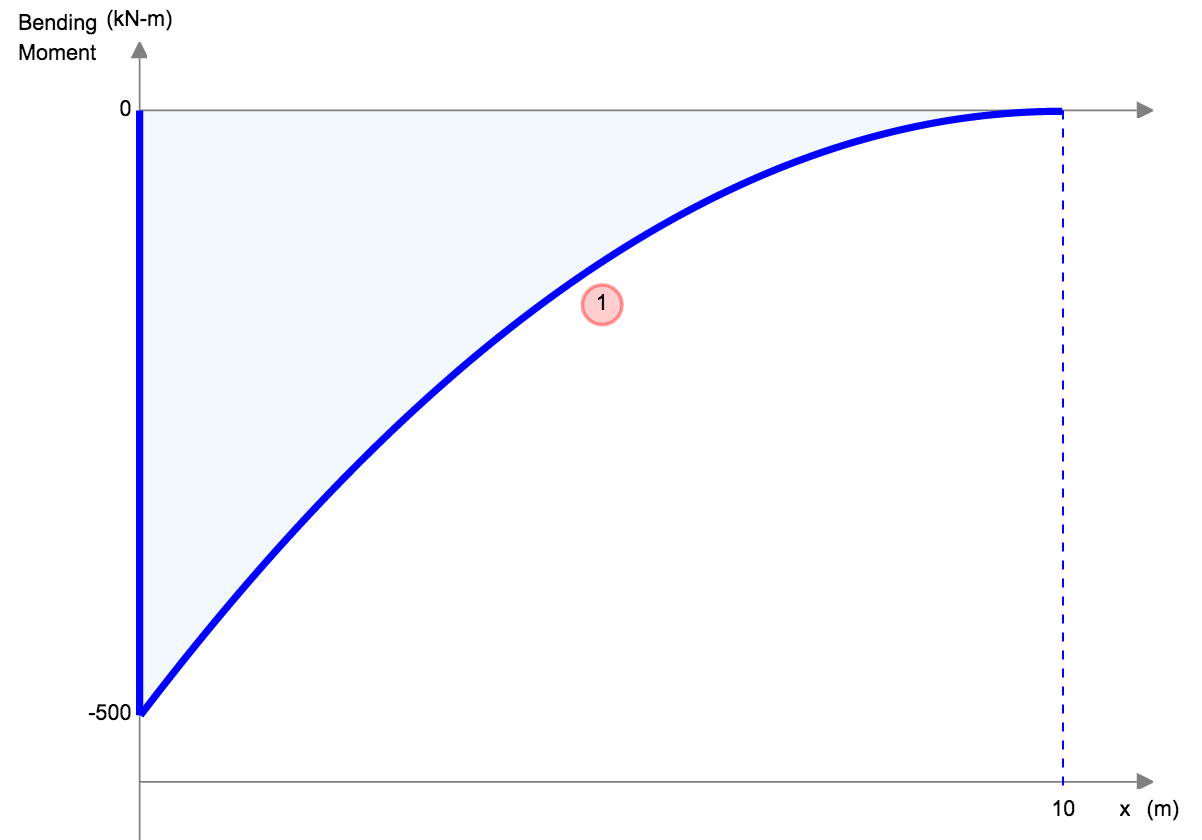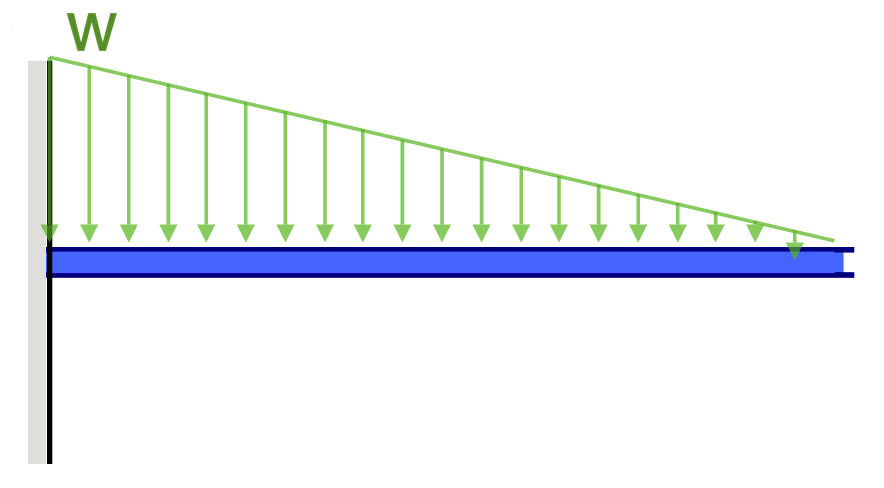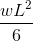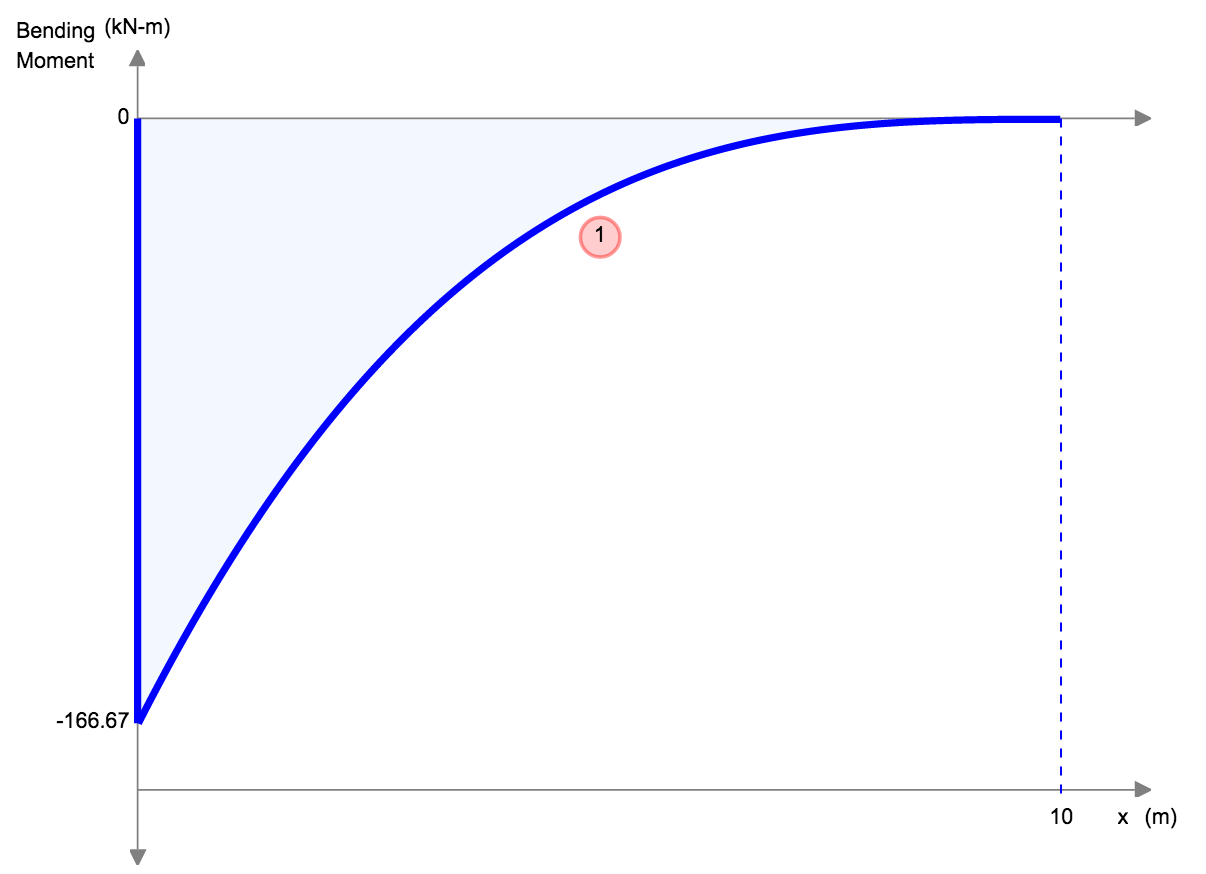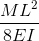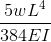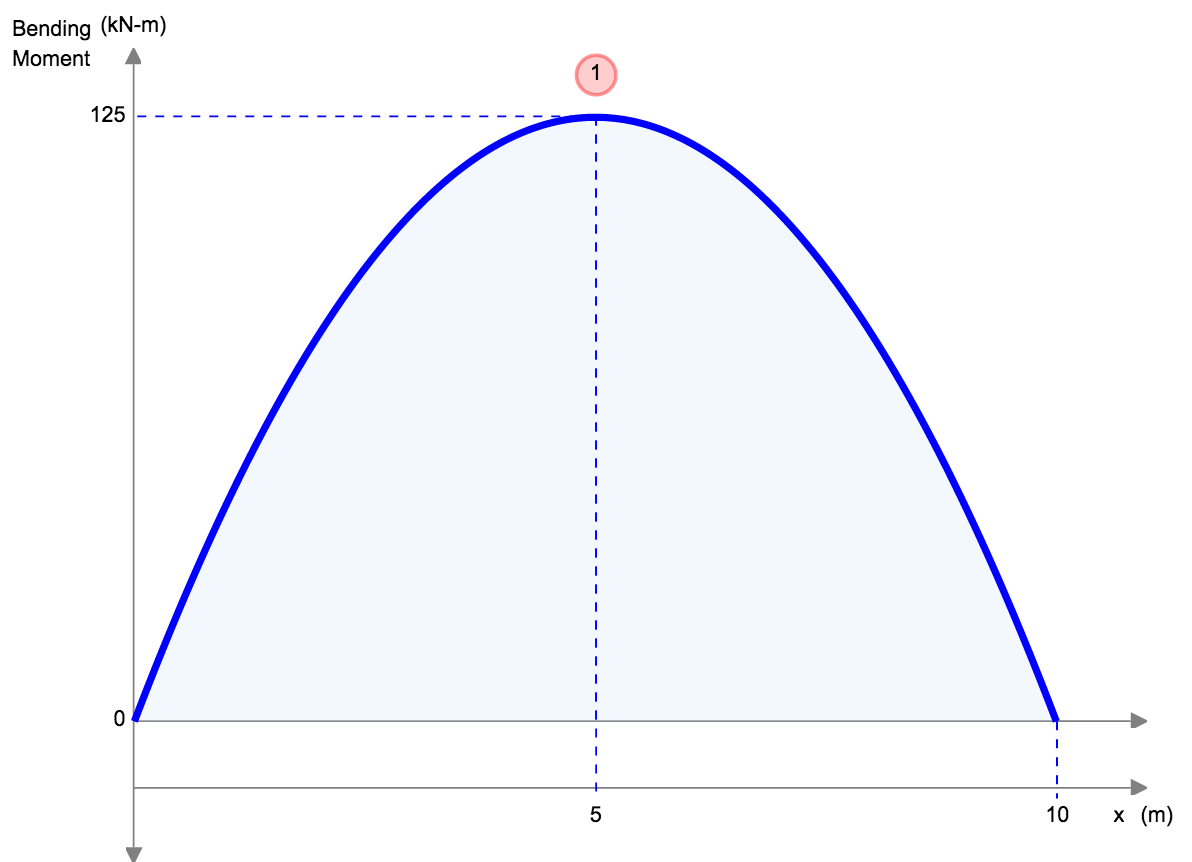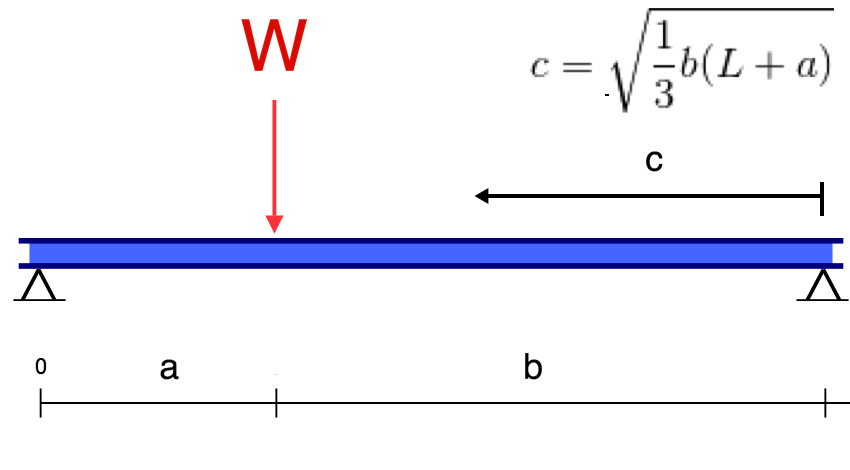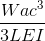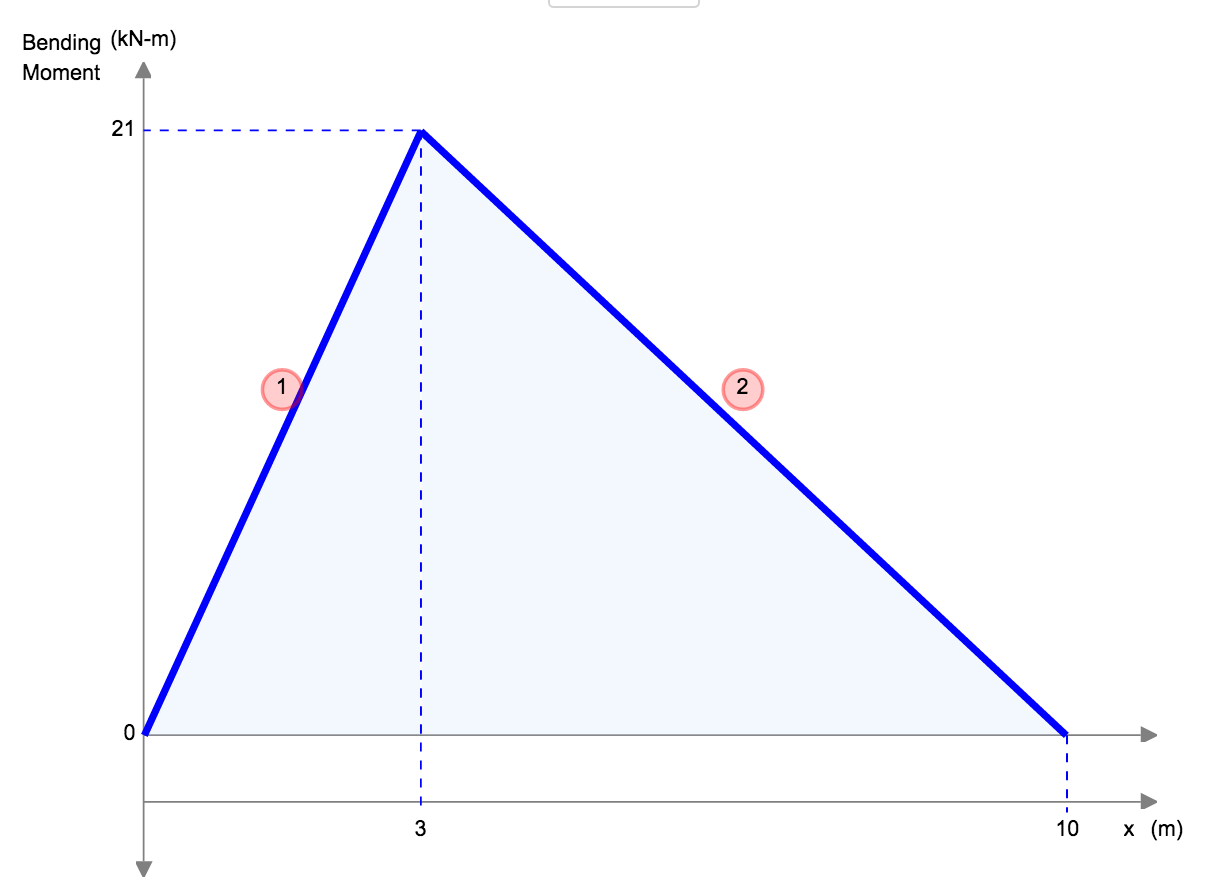Σταθερές Εξισώσεις/Τύπες Παραμόρφωσης Δοκού

 

Αναφορά	Μέγιστη απόκλιση	Σχήμα BMD

 

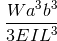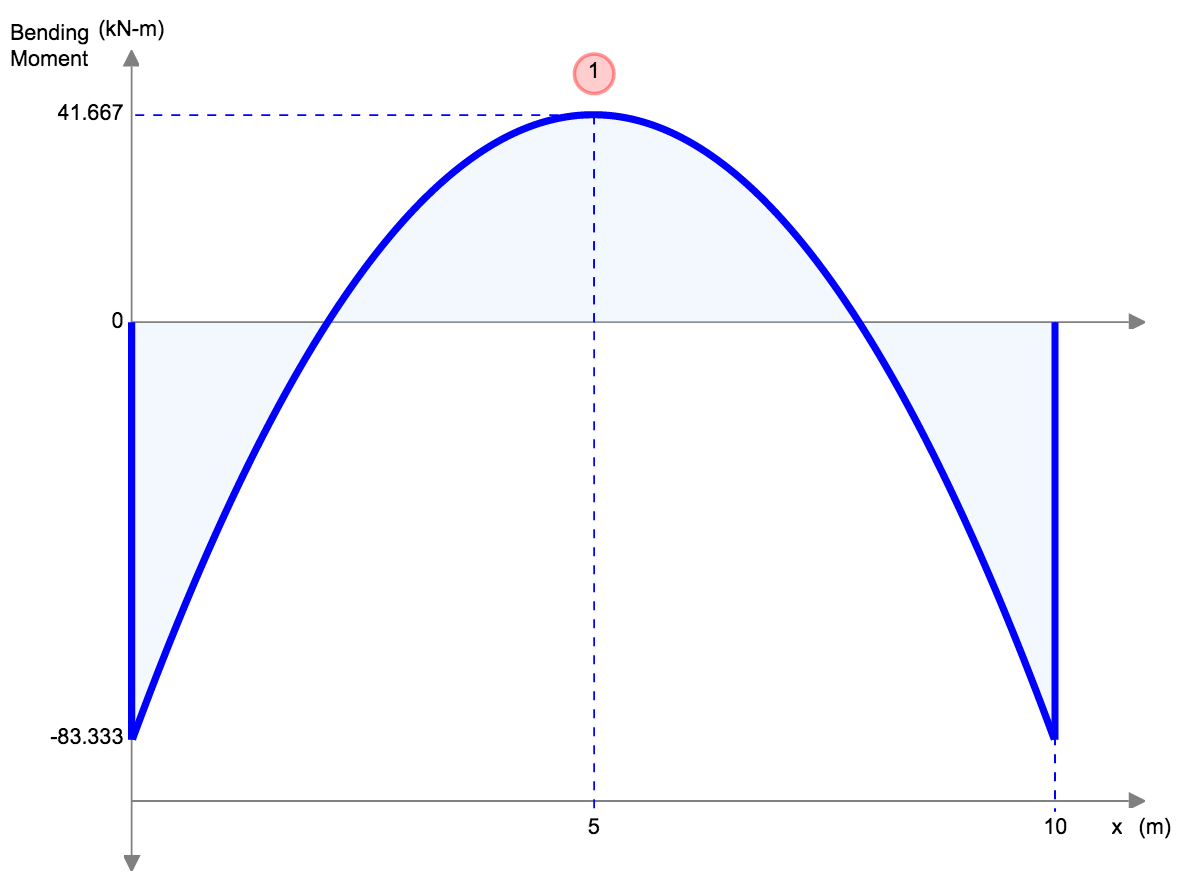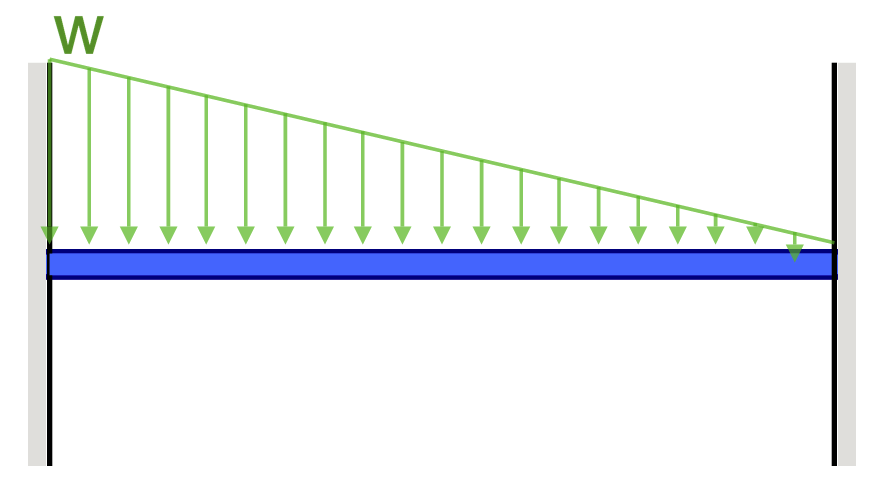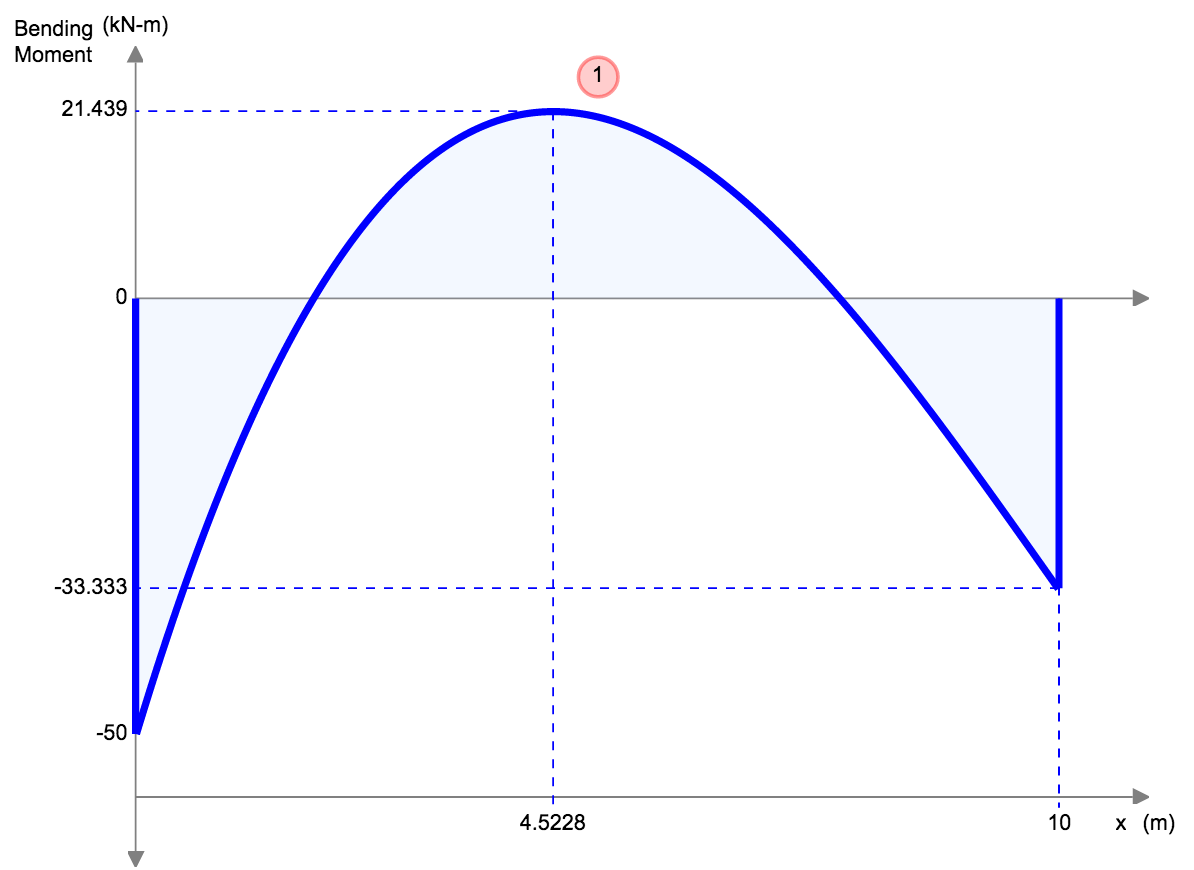4. Παράδειγμα Υπολογισμού Απλώς Υποστηριζόμενης Δέσμης

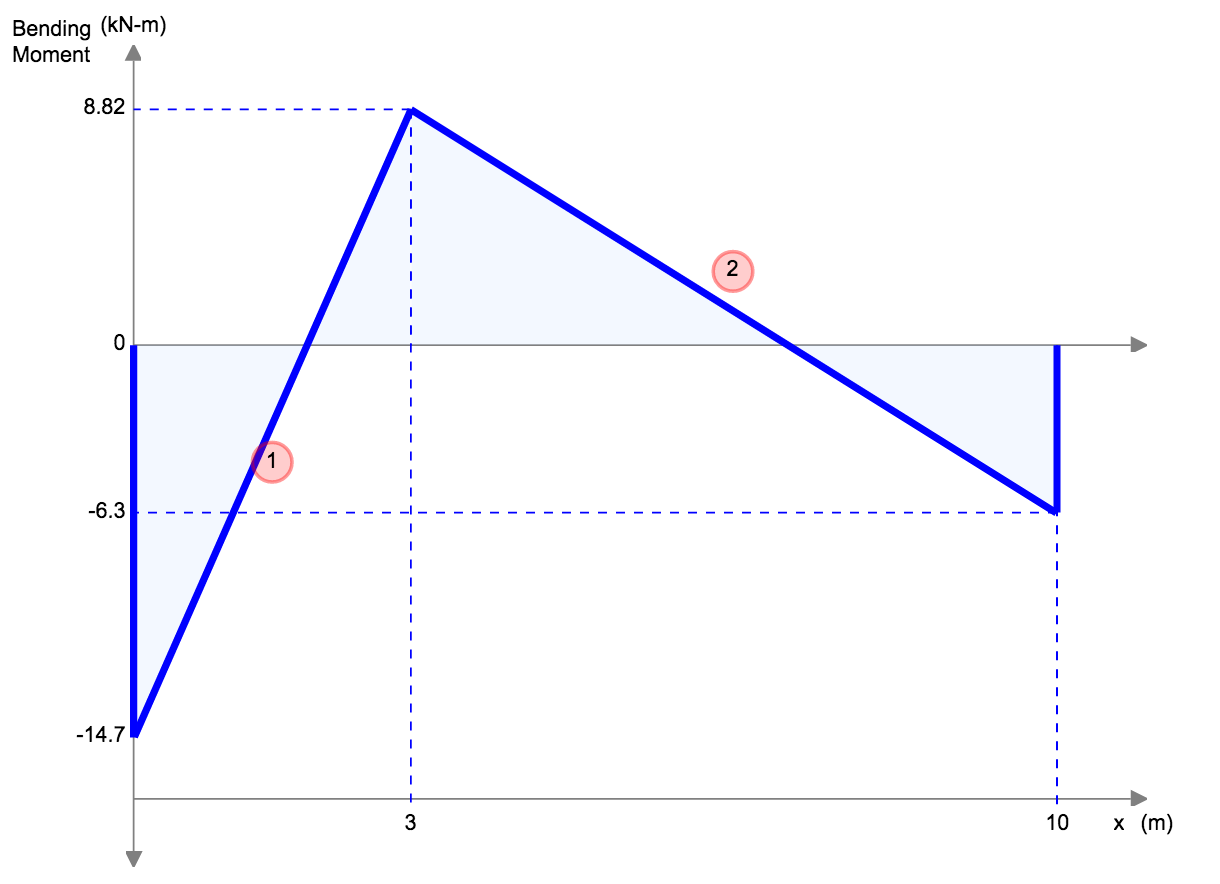
Ας εξετάσουμε μια απλή δοκό στήριξης με άνοιγμα L = 10 Μ, ένα ομοιόμορφο φορτίο w = 10,000 N/m, και τις ακόλουθες ιδιότητες υλικού: μέτρο του Young, Ε = 200 GPa, τη στιγμή της αδράνειας, Ι = 0.0015 m^4.

Η απόκλιση της δοκού μπορεί να υπολογιστεί χρησιμοποιώντας την εξίσωση, παρμένο από τα παραπάνω μας πίνακας εξισώσεων εκτροπής δοκού:

\(δ = (5wl^4)/(384ΟΧΙ) \)

\(δ = (5 * 10,000 * 10^ 4)/(384 * 200 *10^9 * 0.0015) \)

\(δ = 0.00434 m = 4,34 mm \)

Άρα η εκτροπή της δοκού είναι 0.00434 m ή 4.34 χιλ. Είναι πάντα σημαντικό ως μηχανικός να επαληθεύετε το αποτέλεσμά σας, ας συνδέσουμε λοιπόν τους ίδιους αριθμούς στο SkyCiv Υπολογιστής δωρεάν εκτροπής δέσμης:

 

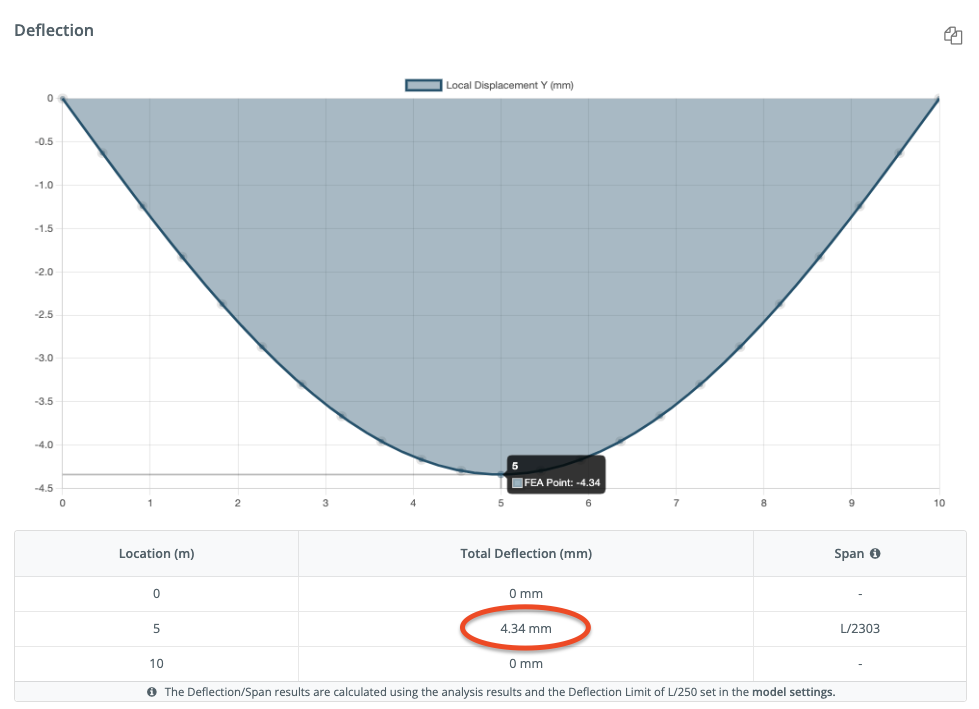
Αξίζει να σημειωθεί ότι αυτό είναι ένα πολύ απλό παράδειγμα και στην πράξη, Υπάρχουν διάφοροι άλλοι παράγοντες που πρέπει να ληφθούν υπόψη, όπως οι επιπτώσεις της αλλαγής της θερμοκρασίας, ζωντανό φορτίο, αυτο-βάρος και πολλά άλλα πράγματα, σε πραγματικό σενάριο, ένας δομικός μηχανικός θα λάμβανε υπόψη αυτούς τους παράγοντες κατά τον υπολογισμό της παραμόρφωσης μιας δοκού.

 

Λογισμικό SkyCiv Beam

Λογισμικό ανάλυσης δέσμης SkyCiv επιτρέπει στους χρήστες να αναλύουν τις δομές δοκών εύκολα και με ακρίβεια. Μπορείτε να λάβετε μια ανάλυση του μέλους δοκού σας, συμπεριλαμβανομένων των αντιδράσεων, δύναμη διάτμησης, στιγμή κάμψης, εκτροπή, και αγχώνεται μέσα σε λίγα δευτερόλεπτα.

Αν θέλετε να το δοκιμάσετε πρώτα, ΔΩΡΕΑΝ μας Υπολογιστής εκτροπής δέσμης είναι ένας πολύ καλός τρόπος για να ξεκινήσετε, ή απλά εγγραφείτε δωρεάν σήμερα!