Φροντιστήριο: Τρόπος επίλυσης δομής ζευκτόντων χρησιμοποιώντας τη μέθοδο των τμημάτων

Σε αυτό το σεμινάριο, θα εξερευνήσουμε και θα μάθουμε τα οφέλη από τη χρήση της μεθόδου των τμημάτων για την επίλυση της δομής ζευκτών σας. Τι είναι τα δοκάρια? Εάν δεν είστε σίγουροι για αυτό, επισκεφθείτε μας Τι είναι ένα ζευκτόν άρθρο. Η μέθοδος των τομών χρησιμοποιείται για την επίλυση μεγαλύτερων δομών ζευκτών σε μια γρήγορη, απλός τρόπος. Περιλαμβάνει τη λήψη «περικοπής»’ μέσω ενός αριθμού μελών για να αξιολογήσουν τις αξονικές τους δυνάμεις και να το χρησιμοποιήσουν ως βάση μας για την επίλυση της υπόλοιπης δομής των ζευκτόντων.

Το σπουδαίο είναι, Προσθήκη απεριόριστων σημείων φορτίων το κάνει αυτόματα για εσάς. Μοντελοποιήστε τα δικά σας ζευκτά και το λογισμικό θα εμφανίσει διαδραστική, βήμα προς βήμα επεξεργασία της μεθόδου των τμημάτων!

Παρακολουθήστε το εκπαιδευτικό βίντεο

Δείγμα ερώτησης

Για το λειτουργικό μας παράδειγμα, θα εξετάσουμε την παρακάτω ερώτηση:

Ερώτηση: Χρησιμοποιώντας τη μέθοδο των ενοτήτων, καθορίζει τις δυνάμεις στα μέλη 10, 11, και 13 της ακόλουθης δομής δοκών:

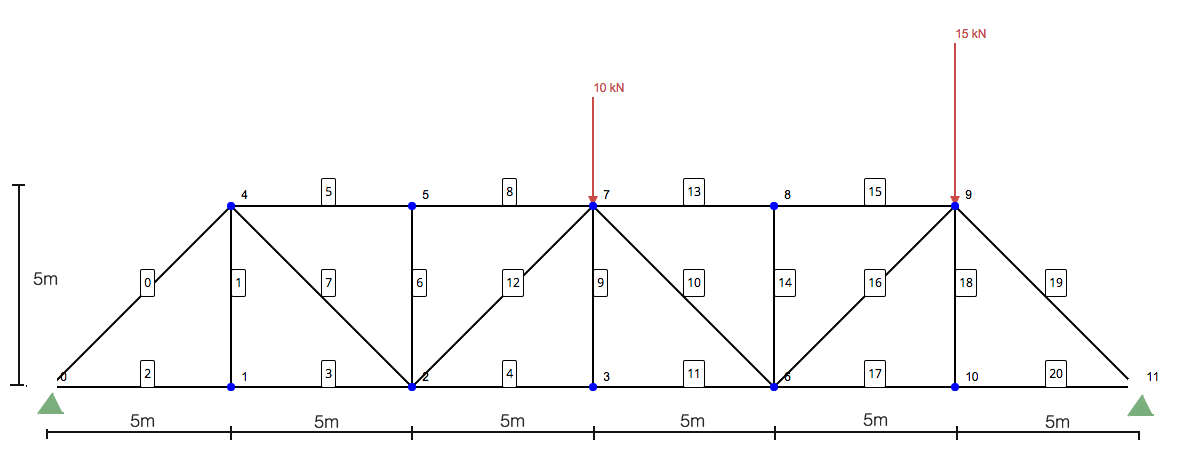
Βήμα 1: Υπολογίστε τις αντιδράσεις στα στηρίγματα

Όπως οι περισσότερες στατικές δομικές αναλύσεις, πρέπει πρώτα να ξεκινήσουμε με τον εντοπισμό και την επίλυση του αντιδράσεις σε υποστηρίγματα. Αυτό θα μας δώσει τις οριακές προϋποθέσεις που πρέπει να προχωρήσουμε στην επίλυση της δομής των ζευκτόντων. Απλοποίηση της δομής ώστε να περιλαμβάνονται μόνο τα φορτία και τα στηρίγματα:

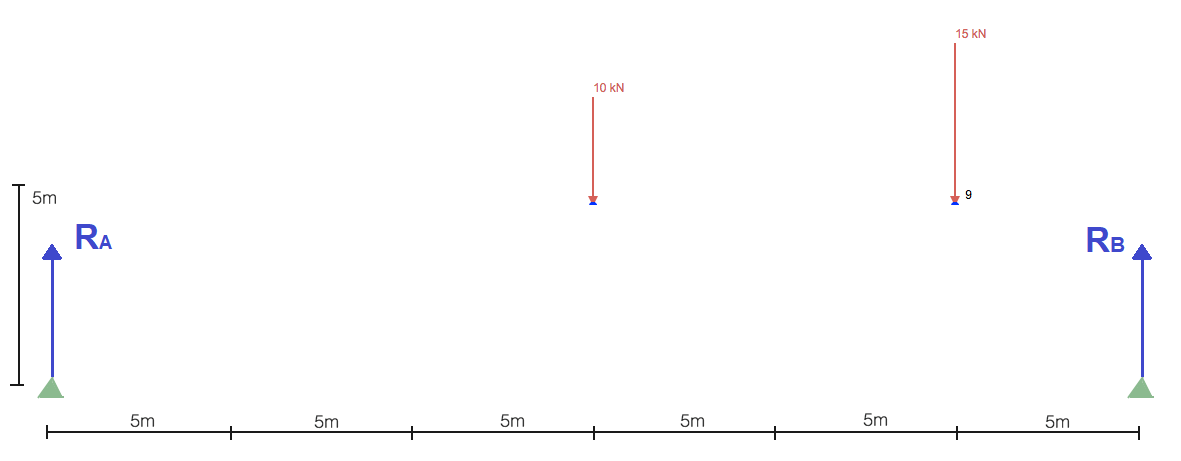
Χωρίς να ξοδεύουμε πολύ χρόνο για τον υπολογισμό των αντιδράσεων, αρχίζετε γενικά παίρνοντας το άθροισμα των στιγμών για ένα σημείο. Παίρνοντας το άθροισμα των στιγμών σχετικά με την αριστερή υποστήριξη μας παίρνει:

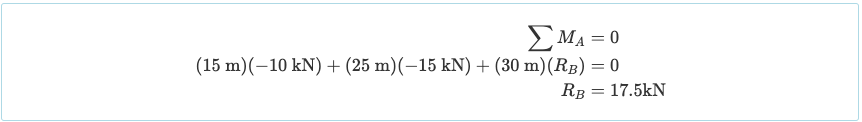
Έτσι, η αντίδραση στη σωστή υποστήριξη (Ρ_σι) είναι 17.5 kN σε ανοδική κατεύθυνση. Τώρα, λαμβάνοντας το άθροισμα των δυνάμεων στο y μας δίνει την αντίδραση R_ΕΝΑ ως 7.5kN σε ανοδική κατεύθυνση:

Βήμα 2: Κάντε μια περικοπή στα μέλη του ενδιαφέροντος

Εδώ έρχεται το πιο σημαντικό μέρος της επίλυσης ενός ζευκτού χρησιμοποιώντας τη μέθοδο των τμημάτων. Περιλαμβάνει να φτιάξετε ένα κομμάτι στα μέλη που θέλετε να λύσετε. Αυτή η μέθοδος δομικής ανάλυσης είναι εξαιρετικά χρήσιμη όταν προσπαθείτε να λύσετε μερικά από τα μέλη χωρίς να χρειάζεται να λύσετε ολόκληρη τη δομή χρησιμοποιώντας τη μέθοδο των αρθρώσεων. Έτσι, στο παράδειγμά μας εδώ θα ήταν η φέτα μας:

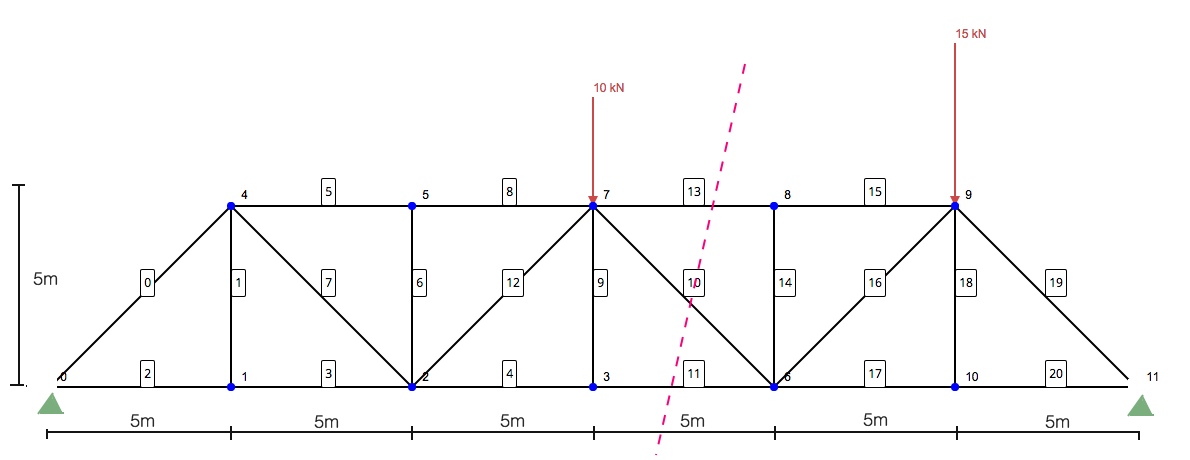
Εστίαση μόνο στην αριστερή πλευρά, μένετε με την ακόλουθη δομή:

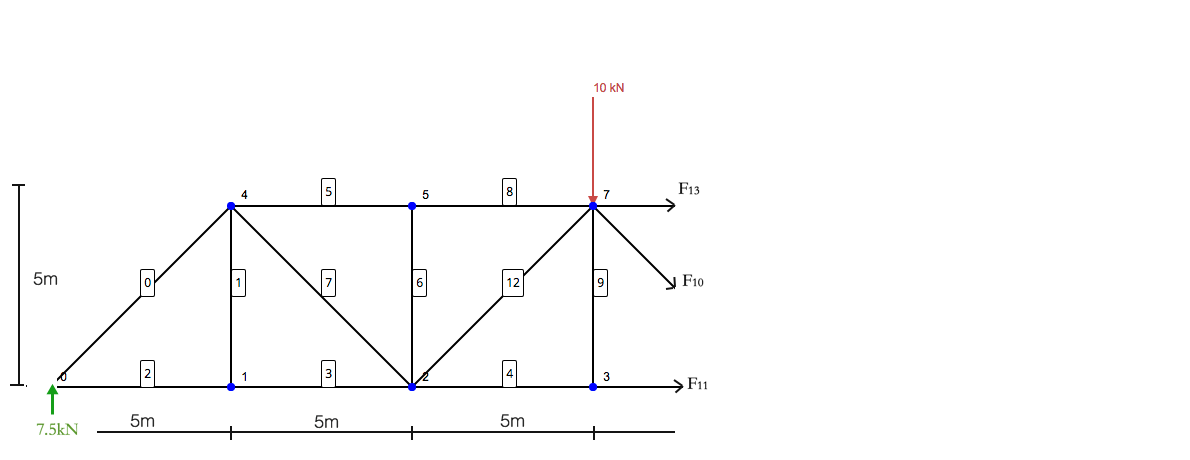
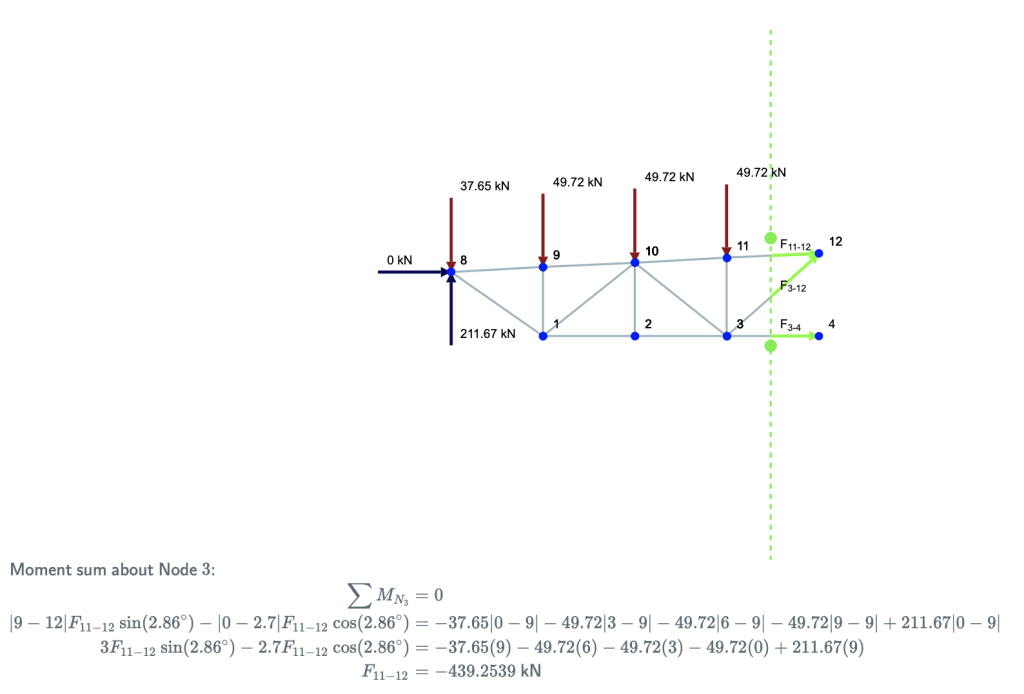
Τώρα σκεφτείτε αυτή τη δομή ως μια μονόπλευρη κατασκευή. Οι νόμοι της στατικής εξακολουθούν να ισχύουν – έτσι το άθροισμα των στιγμών και των δυνάμεων πρέπει να είναι ίσο με το μηδέν. Τα μέλη με βέλη (φά₁₃, φά₁₀, φά₁₁) είναι αυτό που σταθεροποιεί την αντίδραση και τις δυνάμεις που ασκούνται στη δομή. Σημειώστε ότι το άθροισμα των στιγμών λαμβάνεται για τον κόμβο 7 – όπως θα αποκλείσει τις δυνάμεις των μελών 13 και 10 – αφήνοντας τον F₁₁ να απομονωθεί.

Χρησιμοποιώντας το παραπάνω διάγραμμα ελεύθερου σώματος, μπορούμε να λάβουμε τους ακόλουθους τύπους:

Άθροισμα δυνάμεων στην κατεύθυνση y:

[μαθηματικά]
\να αρχίσει{ευθυγραμμίζω}
+\επάνω κείμενο{ } \άθροισμα{F_y} &= 0\\
7.5\κείμενο{ ΚΝ} – 10 \κείμενο{ ΚΝ} – ΦΑ_{10}χωρίς(45^{\κυκλ}) &= 0\\
ΦΑ_{10} &= -3.536 \κείμενο{ ΚΝ}
\τέλος{ευθυγραμμίζω}
[μαθηματικά]

Άθροισμα στιγμών για κόμβο 7:

[μαθηματικά]
\να αρχίσει{ευθυγραμμίζω}
+\κύκλος αριστερό κείμενο{ } \άθροισμα{M_7} &= 0\\
-(15 \κείμενο{ Μ})(7.5 \κείμενο{ ΚΝ}) + (5 \κείμενο{ Μ})ΦΑ_{11} &= 0\\
ΦΑ_{11} &= 22.5 \κείμενο{ ΚΝ}
\τέλος{ευθυγραμμίζω}
[μαθηματικά]

Άθροισμα δυνάμεων στην κατεύθυνση x:

[μαθηματικά]
\να αρχίσει{ευθυγραμμίζω}
+\δεξί βέλος κείμενο{ } \άθροισμα{F_x} &= 0\\
ΦΑ_{13} + ΦΑ_{11} + ΦΑ_{10}συν(45^{\κυκλ}) &= 0\\
ΦΑ_{13} &= -F_{11} – ΦΑ_{10}συν(45^{\κυκλ}) \\
ΦΑ_{13} &= – (22.5 \κείμενο{ ΚΝ}) – (-3.536 \κείμενο{ ΚΝ})συν(45^{\κυκλ}) \\
ΦΑ_{13} &= -22.5 \κείμενο{ ΚΝ} + (3.536 \κείμενο{ ΚΝ})συν(45^{\κυκλ}) \\
ΦΑ_{13} &= -20 \κείμενο{ ΚΝ}
\τέλος{ευθυγραμμίζω}
[μαθηματικά]

ΤΕΛΙΚΗ λυση

Μπορούμε να χρησιμοποιήσουμε αυτά τα αποτελέσματα για να επιλύσουμε τα υπόλοιπα μέλη στη δομή των δοκών. Ελπίζουμε ότι αυτό το παράδειγμα υπολογισμού ζευκτών ήταν χρήσιμο και μην διστάσετε να σχολιάσετε τις ερωτήσεις σας παρακάτω. Ως αναφορά, Τα αποτελέσματα για ολόκληρη τη δομή ζευκτόντων βρίσκονται παρακάτω (χρησιμοποιώντας μας Υπολογιστής ζευκτόντων) που είναι εξαιρετικό για τον έλεγχο των απαντήσεων σας!

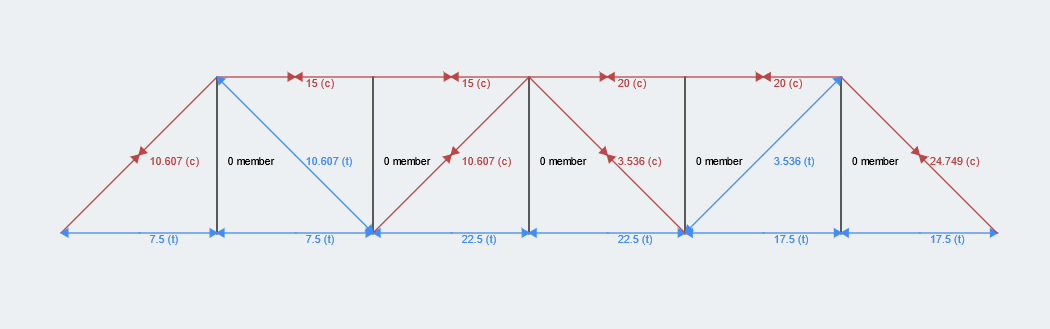
Περίληψη Βημάτων

• Ξεκινήστε πάντα υπολογίζοντας τις αντιδράσεις σε υποστηρίγματα
• Κάντε ένα κομμάτι στα μέλη που θέλετε να λύσετε
• Αντιμετωπίστε τη μισή δομή ως το δικό της στατικό στήριγμα
• Λύστε το στήριγμα λαμβάνοντας το άθροισμα των δυνάμεων = 0
• Αφιερώστε λίγο χρόνο για έναν κόμβο περισσότερων από ένα άγνωστων μελών

Λογισμικό SkyCiv Truss

Ελπίζουμε ότι βρήκατε αυτό το σεμινάριο χρήσιμο για τα έργα σας. Επισκεφθείτε μας φροντιστήρια ζευκτών για περισσότερες χρήσιμες πληροφορίες σχετικά με το ζευκτό και μην ξεχάσετε να ανατρέξετε στο δικό μας οδηγός για την επίλυση ζευκτών με τη μέθοδο των αρμών.

Προσθήκη απεριόριστων σημείων φορτίων μπορεί να υπολογίσει τη μέθοδο των τμημάτων αυτόματα για εσάς. Ή δοκιμάστε το δικό μας Δωρεάν Υπολογιστής ζευκτόντων που θα σου δώσει την τελική απάντηση (χωρίς υπολογισμούς με το χέρι).

Για να εξερευνήσετε περισσότερη λειτουργικότητα του λογισμικού SkyCiv, εγγραφείτε σήμερα για να ξεκινήσετε!

Ξεκινήστε δωρεάν