Calculation guide in designing an isolated footing based on CSA A23.3-14

SkyCiv Foundation covers the design of isolated footing conforming to CSA A23.3-14¹ and NBCC 2010².

Θέλετε να δοκιμάσετε το λογισμικό Foundation Design του SkyCiv? Το εργαλείο μας επιτρέπει στους χρήστες να εκτελούν υπολογισμούς Foundation Design χωρίς λήψη ή εγκατάσταση!

Υπολογιστής σχεδίασης ιδρύματος

Παράμετροι σχεδίασης ενός απομονωμένου ποδιού

Some calculations presented are similar with ACI 318, which is also one of the references of its CSA counterpart.

Απαιτήσεις διάστασης

Για τον προσδιορισμό των διαστάσεων μιας απομονωμένης βάσης, σέρβις ή ατέλειωτα φορτία, όπως νεκρός (ρε), Ζω (μεγάλο), Ανεμος (Δ), Σεισμικός (μι), κ.λπ. θα εφαρμοστούν χρησιμοποιώντας συνδυασμούς φορτίων, as defined by NBCC 2010. Ό, τι κι αν συνδυάζει φορτίο θα θεωρείται το φορτίο σχεδιασμού, and will be divided to the allowable soil pressure as shown in Equation 1.

\(\κείμενο{ΕΝΑ} = frac{\κείμενο{Π}_{\κείμενο{ν}}}{\κείμενο{ε}_{\κείμενο{όλα}}} \δεξί βέλος \) Εξίσωση 1

όπου:
ε_όλα = επιτρεπόμενη πίεση εδάφους
Π_ν = μη παραγοντωτό φορτίο σχεδιασμού
A = Περιοχή ιδρύματος

Μονόδρομη κουρά

To check for Διαδικτυακός υπολογιστής ποδιών για επιθέματα από σκυρόδεμα, the Critical Shear Plane (Ανατρέξτε στην Εικόνα 1) βρίσκεται σε απόσταση “ρε” από το πρόσωπο μιας στήλης.

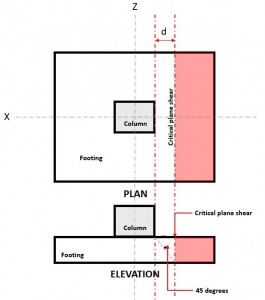
Φιγούρα 1. Κρίσιμο επίπεδο διάτμησης μονόδρομης διάτμησης

ο Μονόδρομος Κουρεύω Ζήτηση ή Β_φά υπολογίζεται με την προϋπόθεση ότι το πέλμα έχει προεξοχή μακριά από τη στήλη όπου βρίσκεται η περιοχή (το κόκκινο) υποδεικνύεται στο σχήμα 2, σύμφωνα με το CSA A23.3-14, Ενότητα 13.3.6.

ο Χωρητικότητα διάτμησης μονής κατεύθυνσης ή Β_ντο ορίζεται ως η τελική ισχύς διάτμησης και υπολογίζεται χρησιμοποιώντας την εξίσωση 2 ανά CSA A23.3-14, Ενότητα 11.3.4.

\(\κείμενο{Β}_{\κείμενο{ντο}} = phi _{\κείμενο{ντο}} \φορές lambda φορές sqrt{\κείμενο{φά'}_{\κείμενο{ντο}}} \φορές κείμενο{σι}_{\κείμενο{β}} \φορές κείμενο{ρε} \δεξί βέλος \) Εξίσωση 2 (CSA A23.3-14 Eq. 11-6)

όπου:
ϕ_ντο = resistance factor for concrete
λ = modification factor for concrete density
φά’_ντο = καθορισμένη αντοχή σκυροδέματος, MPa
σι_β = πλάτος της βάσης, χιλ
d = effective shear depth, χιλ

Shear Demand and Shear Capacity must meet the following equation to meet the design requirements of CSA A23.3-14:

\(\κείμενο{Β}_{\κείμενο{φά}} \leq phi κείμενο{Β}_{\κείμενο{ντο}} \δεξί βέλος \) Εξίσωση 3 (CSA A23.3-14 Εξ. 11.3)

Ίδρυμα SkyCiv, σύμφωνα με την εξίσωση 3, υπολογίζει τη μονόδρομη αναλογία διατμητικής ενότητας (Εξίσωση 4) λαμβάνοντας το Shear Demand πάνω από το Shear Capacity.

\( \κείμενο{Αναλογία ενότητας} = frac{\κείμενο{Διατμητική ζήτηση}}{\κείμενο{Ικανότητα διάτμησης}} \δεξί βέλος \) Εξίσωση 4

Αμφίδρομη κουρά

ο Αμφίδρομη κουρά οριακή κατάσταση, γνωστός και ως διάτμηση διάτμησης, επεκτείνει το κρίσιμο τμήμα του σε απόσταση “δ/2” από την όψη της στήλης και περιμετρικά της στήλης. Το κρίσιμο επίπεδο διάτμησης βρίσκεται σε αυτό το τμήμα της βάσης (Ανατρέξτε στην Εικόνα 2).

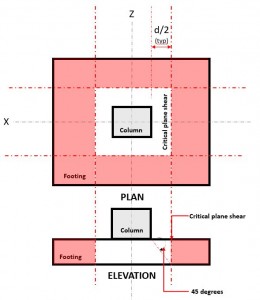
Φιγούρα 2. Κρίσιμο επίπεδο διάτμησης αμφίδρομης διάτμησης

ο Δύο τρόποιάκου Ζήτηση ή Β_φά εμφανίζεται στο κρίσιμο επίπεδο διάτμησης, located a distance of “δ/2” όπου το (το κόκκινο) εκκολαφθείσα περιοχή, υποδεικνύεται στο σχήμα 2, σύμφωνα με το CSA A23.3-14, Ενότητα 13.3.3.

ο Ικανότητα διάτμησης ή Β_ντο is governed by the least value calculated using Equation 5, 6, και 7 ανά CSA A23.3-14, Ενότητα 13.3.4.1

\(\κείμενο{Β}_{\κείμενο{ντο}} = αριστερά ( 1 + \frac{2}{\βήτα_{\κείμενο{ντο}}} \σωστά ) \φορές 0.19 \times \lambda \times \phi _{\κείμενο{ντο}} \φορές sqrt{φά'_{ντο}} \δεξί βέλος \) Εξίσωση 5 (CSA A23.3-14 Εξ. 13.5)

\(\κείμενο{Β}_{\κείμενο{ντο}} = αριστερά ( \frac{\άλφα_{\κείμενο{μικρό}} \φορές κείμενο{ρε}}{\κείμενο{σι}_{\κείμενο{ο}}} + 0.19 \σωστά ) \times \lambda \times \phi _{\κείμενο{ντο}} \φορές sqrt{φά'_{ντο}} \δεξί βέλος \) Εξίσωση 6 (CSA A23.3-14 Εξ. 13.6)

\(\κείμενο{Β}_{\κείμενο{ντο}} = 0.38 \times \lambda \times \phi _{\κείμενο{ντο}} \φορές sqrt{φά'_{ντο}} \δεξί βέλος \) Εξίσωση 7 (CSA A23.3-14 Εξ. 13.7)

Σημείωση: β_ντο is the ratio of long side to short side of the column, συμπυκνωμένο φορτίο, ή περιοχή αντίδρασης και α_μικρό δίνεται από 13.3.4.1

όπου:
λ = modification factor for concrete density
φά’_ντο = specified compressive concrete strength, MPa
d = απόσταση από ακραίες ίνες συμπίεσης έως κεντροειδές οπλισμό διαμήκους τάσης, χιλ

Shear Demand and Shear Capacity must meet the following equation to meet the design requirements of CSA A23.3-14:

\(\κείμενο{Β}_{\κείμενο{φά}} \leq phi κείμενο{Β}_{\κείμενο{ντο}} \δεξί βέλος \) Εξίσωση 8 (CSA A23.3-14 Εξ. 11.3)

Ίδρυμα SkyCiv, σύμφωνα με την εξίσωση 8, υπολογίζει την αμφίδρομη αναλογία διατμητικής ενότητας (Εξίσωση 9) λαμβάνοντας το Shear Demand πάνω από το Shear Capacity.

\( \κείμενο{Αναλογία ενότητας} = frac{\κείμενο{Διατμητική ζήτηση}}{\κείμενο{Ικανότητα διάτμησης}} \δεξί βέλος \) Εξίσωση 9

Κάμψη

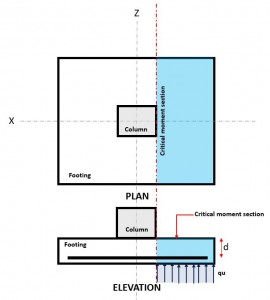
Φιγούρα 3. Τμήμα Κρίσιμης Κάμψης

ο Κάμψη οριακή κατάσταση εμφανίζεται στο το τμήμα κρίσιμης κάμψης, βρίσκεται στην πρόσοψη της στήλης στην κορυφή του υποστρώματος (Ανατρέξτε στην Εικόνα 3).

ο Moment Demand, ή Μ_φά βρίσκεται στο τμήμα κρίσιμης κάμψης (μπλε καταπακτή) υποδεικνύεται στο σχήμα 3, και υπολογίζεται χρησιμοποιώντας την εξίσωση 10.

\( \κείμενο{Μ}_{εσύ} = κείμενο{ε}_{εσύ} \φορές αριστερά ( \frac{μεγάλο_{Χ}}{2} – \frac{ντο_{Χ}}{2} \σωστά ) \φορές l_{με} \φορές αριστερά ( \frac{\frac{μεγάλο_{Χ}}{2} – \frac{ντο_{Χ}}{2} }{2} \σωστά ) \δεξί βέλος \) Εξίσωση 10

όπου:
ε_εσύ = συντελεστής πίεσης του εδάφους, kPa
μεγάλο_Χ = διάσταση βάσης κατά μήκος του άξονα x, χιλ
μεγάλο_με = διάσταση βάσης κατά μήκος του άξονα z, χιλ
ντο_Χ = διάσταση στήλης κατά μήκος του άξονα x, χιλ

ο Moment Resistance, ή Μρ υπολογίζεται χρησιμοποιώντας την εξίσωση 11.

\( \κείμενο{Μ}_{ρ} = phi_{\κείμενο{μικρό}} \φορές A_{μικρό} \φορές f_{και} \φορές αριστερά( ρε – \frac{ένα}{2} \σωστά) \δεξί βέλος \) Εξίσωση 11

όπου:
ϕ_μικρό = resistance factor for non-prestressed reinforcing bars
d = απόσταση από ακραίες ίνες συμπίεσης έως κεντροειδές οπλισμό διαμήκους τάσης, χιλ
ΕΝΑ_μικρό = περιοχή ενίσχυσης, χιλ²
a = βάθος ισοδύναμου ορθογώνιου μπλοκ τάσης, χιλ
fy = αντοχή οπλισμού, MPa

NEW SkyCiv Foundation with FEA

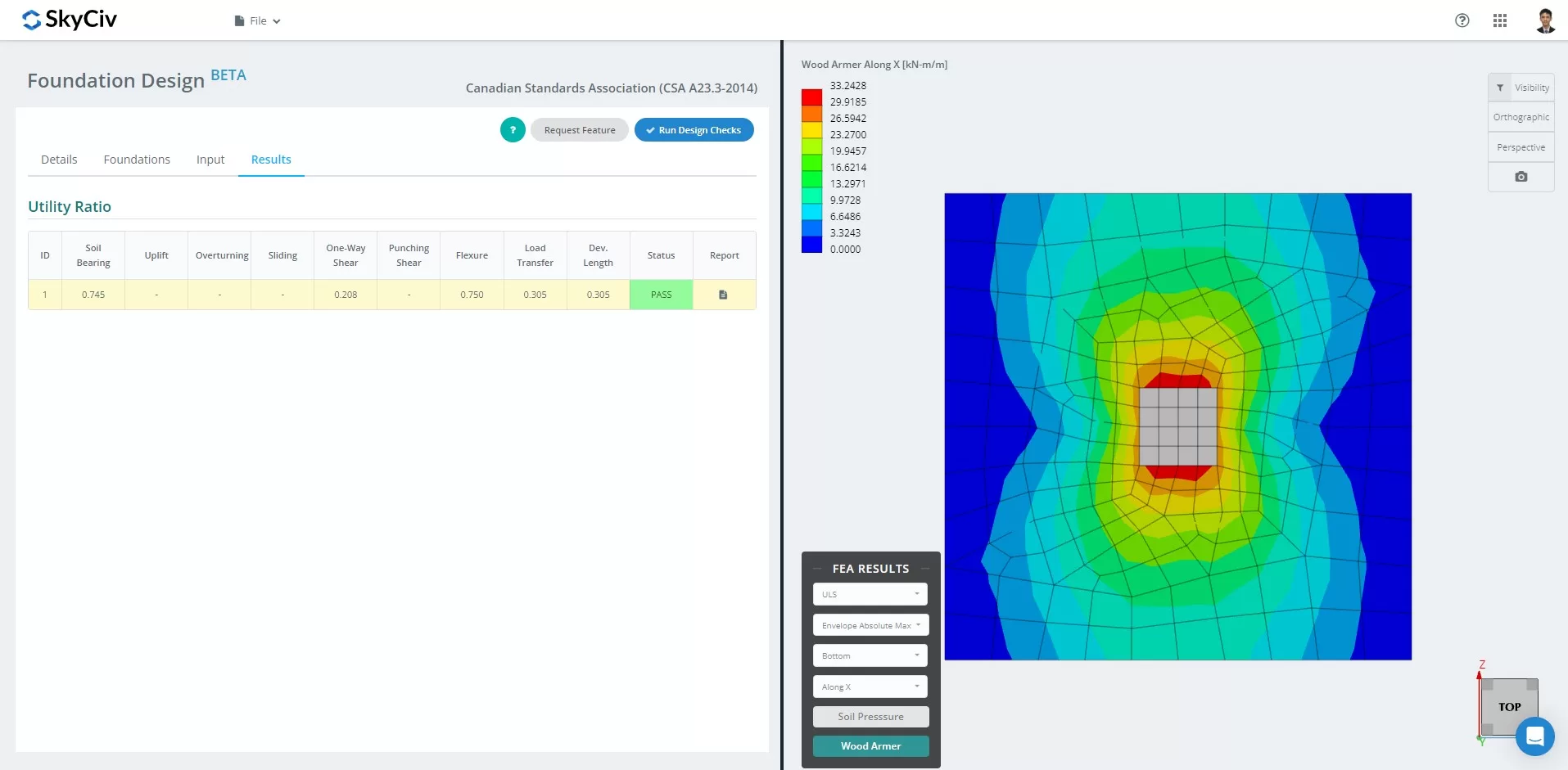
As of March 2024, the Foundation Design Module has integrated the Finite Element Analysis (ΑΣΧΗΜΟΣ) solver into its capabilities. This new feature allows users to conduct in-depth soil pressure and wood armer analyses while still performing all structural checks specified by CSA A23.3-14, including all verifications mentioned above. Summary of the FEA Results is included in the comprehensive report.