Ένα πλήρως λειτουργικό παράδειγμα του NBCC 2015 υπολογισμοί φορτίου χιονιού
Η συσσώρευση χιονιού σε κατασκευές μπορεί να είναι πολύ επικίνδυνη για τα μέλη της στέγης ή άλλα εκτεθειμένα δομικά στοιχεία. ο Εθνικός Κώδικας του Καναδά (2015) Τμήμα Β – Ενότητα 4.1.6 παρέχει λεπτομερή υπολογισμό των φορτίων χιονιού και των σχετικών φορτίων βροχής. Χρησιμοποιώντας αυτήν την οδηγία, θα δείξουμε πώς να υπολογίσουμε τα φορτία χιονιού χρησιμοποιώντας ένα παράδειγμα Structural 3D (S3D) μοντέλο αποθήκης, όπως φαίνεται παρακάτω:
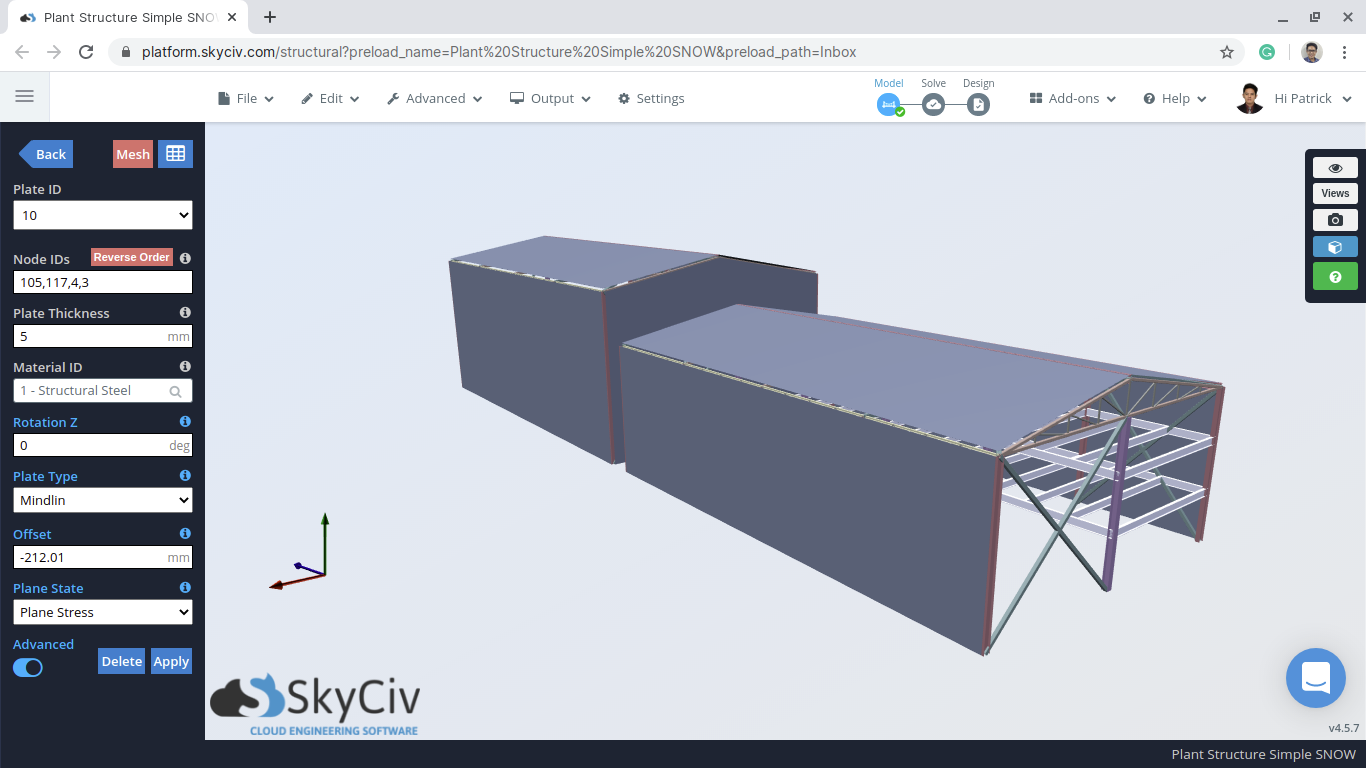
Φιγούρα 1: Παράδειγμα μοντέλου αποθήκης S3D

Φιγούρα 2: Παράδειγμα τοποθεσίας ιστότοπου με χρήση των Χαρτών Google (μόνο για απεικόνιση).
Τραπέζι 1: Απαιτούνται δεδομένα δόμησης για τον υπολογισμό του φορτίου χιονιού.
| Τοποθεσία | Όγκντεν, Κάλγκαρι, Αλμπέρτα (μόνο για απεικόνιση) |
| Χωρητικότητα | Αποθήκη ή αποθήκευση υλικών |
| Διαστάσεις | 19.508 μ x 31.70 m για κάθε δομή Ύψος μαρκαδόρου μικρότερου κτηρίου 9.144 Μ Ύψος κορυφής μικρότερου κτηρίου 11.941 Μ Η διαφορά της άνω και κάτω οροφής είναι 3.50 Μ Γωνία βήματος οροφής 16° |
| Επιπλέον Λεπτομέρειες | Η οροφή έχει ολισθηρή επιφάνεια Το κενό μεταξύ των δομών είναι 2.30 Μ |
Από τον πίνακα 1, το καθορισμένο φορτίο χιονιού, \(ΜΙΚΡΟ), μπορεί να υπολογιστεί χρησιμοποιώντας τον τύπο:
\(S = {Εγώ}_{μικρό}[{μικρό}_{μικρό}{ντο}_{σι}{ντο}_{β}{ντο}_{μικρό}{ντο}_{ένα} +{μικρό}_{ρ}]\) (1)
Οπου:
\({Εγώ}_{μικρό}\) = συντελεστής σημασίας για το φορτίο χιονιού, Πίνακας 4.1.6.2-A
\({μικρό}_{μικρό}\) = 1-φορτίο χιονιού εδάφους σε 50 χρόνια, kPa, Υποδιαίρεση 1.1.3
\({ντο}_{σι}\) = βασικός συντελεστής φορτίου χιονιού οροφής, 4.1.6.2 (2)
\({ντο}_{β}\) = με βάση τον παράγοντα έκθεσης στον άνεμο, 4.1.6.2 (3) και (4)
\({ντο}_{μικρό}\) = συντελεστής κλίσης, 4.1.6.2 (5), (6), και (7)
\({ντο}_{ένα}\) = συντελεστής συσσώρευσης, 4.1.6.2 (8)
\({μικρό}_{ρ}\) = 1-σε-50 σχετικό φορτίο βροχής, kPa, Υποδιαίρεση 1.1.3, αλλά όχι μεγαλύτερο από \({μικρό}_{μικρό}{ντο}_{σι}{ντο}_{β}{ντο}_{μικρό}{ντο}_{ένα}\)
Κάθε παράμετρος θα εξεταστεί ξεχωριστά στις ακόλουθες ενότητες. Θα υπολογιστούν οι ακόλουθες περιπτώσεις φορτίου χιονιού: ισορροπημένο και μη ισορροπημένο φορτίο χιονιού σε κάθε στέγη (φυσιολογικός άνεμος στην κορυφογραμμή), καθώς και την κλίση που δημιουργείται στην κάτω οροφή λαμβάνοντας υπόψη τη συσσώρευση από την ολίσθηση.
Συντελεστής σημασίας, \({Εγώ}_{μικρό}\)
Το πρώτο πράγμα που καθορίζεται είναι ο παράγοντας σημασίας, \({Εγώ}_{μικρό}\), που βρίσκεται χρησιμοποιώντας Πίνακας 4.1.6.2-A όπως αναφέρεται. Δεδομένου ότι η δομή είναι ένα κτίριο αποθήκευσης που έχει χαμηλό άμεσο αντίκτυπο στην ανθρώπινη ζωή σε περίπτωση αποτυχίας, η κατηγορία σπουδαιότητας είναι Χαμηλός. Εξάλλου, ο υπολογισμός θα γίνει στο Ultimate Limit State (ULS). Έτσι από Πίνακας 4.1.6.2-A, \({Εγώ}_{μικρό}\) είναι ίσο με 0.80.
| Κατηγορία σπουδαιότητας | Συντελεστής σημασίας, \({Εγώ}_{μικρό}\) | |
|---|---|---|
| ULS | SLS | |
| Χαμηλός | 0.8 | 0.9 |
| Κανονικός | 1.0 | 0.9 |
| Υψηλός | 1.15 | 0.9 |
| Μετά την καταστροφή | 1.25 | 0.9 |
Φορτίο χιονιού εδάφους, \({μικρό}_{μικρό}\), και σχετικό φορτίο βροχής, \(({μικρό}_{ρ})\)
Το φορτίο χιονιού εδάφους, \({μικρό}_{μικρό}\), και σχετικό φορτίο βροχής, \(({μικρό}_{ρ})\), οι τιμές καταγράφονται σε Προσάρτημα Γ, Τμήμα Β του NBCC 2015 ανάλογα με την τοποθεσία και την επαρχία. Για αυτό το παράδειγμα, το αντίστοιχο \({μικρό}_{μικρό}\) και \(({μικρό}_{ρ})\) σε Κάλγκαρι Αλμπέρτα είναι ίσο με 1.10 kPa και 0.1 kPa, αντίστοιχα.
Δυσκολεύεστε να αναζητήσετε το χιόνι στο έδαφος και το σχετικό φορτίο βροχής για NBCC 2015? Προσπαθήστε ο Εργαλείο γεννήτριας δωρεάν φορτίου SkyCiv για να επιταχύνετε την αναζήτησή σας και να λάβετε το αντίστοιχο \({μικρό}_{μικρό}\) και \({μικρό}_{ρ}\) με βάση την τοποθεσία της δομής σας.
Συντελεστής έκθεσης ανέμου, \({ντο}_{β}\)
Για τον παράγοντα έκθεσης στον άνεμο, \({ντο}_{β}\), επιτρέπεται να είναι ίσο με 1.0 βασισμένο στο 4.1.6.2 (3). Αυτός ο παράγοντας μπορεί να μειωθεί όσο οι συνθήκες στο 4.1.6.2 (4) είναι ικανοποιημένος. Για αυτό το παράδειγμα, \({ντο}_{β}\) ισούται με 1.0 αφού η τοποθεσία δεν είναι ανοιχτό έδαφος που εκθέτει πλήρως τη δομή στον άνεμο.
Βασικός συντελεστής φορτίου χιονιού οροφής, \({ντο}_{σι}\)
Ο βασικός παράγοντας φορτίου χιονιού στέγης, \({ντο}_{σι}\), μπορεί να υπολογιστεί χρησιμοποιώντας τους ακόλουθους τύπους, όπως αναφέρεται στο 4.1.6.2 (2):
\({ντο}_{σι} = 0.8\) (2) Για \({μεγάλο}_{ντο} ≤ (70/{{ντο}_{β}}^{2})\) και
\({ντο}_{σι} = (1/{ντο}_{β}) [1 – (1 – 0.8{ντο}_{β})λήξη(-0.01({μεγάλο}_{ντο}{{ντο}_{β}}^{2} – 70))] \) (3) Για \({μεγάλο}_{ντο} > (70/{{ντο}_{β}}^{2})\)
Οπου:
\({μεγάλο}_{ντο}\) = χαρακτηριστικό μήκος της άνω ή κάτω οροφής που ορίζεται ως: \(2β -{β}^{2}/μεγάλο)
\(μεγάλο) = μεγαλύτερη διάσταση της οροφής
\(w\) = μικρότερη κάτοψη της οροφής
Για αυτό το παράδειγμα,\(μεγάλο) και \(w\) είναι ίσο με 31.7 μ και 19.51 Μ, αντίστοιχα, ως εκ τούτου, \({μεγάλο}_{ντο}\) είναι ίσο με 27.01. Από \({μεγάλο}_{ντο}\) είναι λιγότερο από \((70/{1.0}^{2})\), ο βασικός συντελεστής φορτίου χιονιού οροφής, \({ντο}_{σι}\), είναι ίσο με 0.8.
Παράγοντας κλίσης, \({ντο}_{μικρό}\)
Ο υπολογισμός του συντελεστή κλίσης είναι \({ντο}_{μικρό}\) αναλυτικό σε 4.1.6.2 (5), (6), και (7) φαίνεται παρακάτω.
Για ανεμπόδιστη ολισθηρή οροφή:
\({ντο}_{μικρό} = 1.0\) Για \(α ≤ 15°\)
\({ντο}_{μικρό} = 0\) Για \(α > 60°\)
\({ντο}_{μικρό} = (60° – α)/45°\) Για \(15° < α ≤ 60°\)
Για άλλες περιπτώσεις:
\({ντο}_{μικρό} = 1.0\) Για \(α ≤ 30°\)
\({ντο}_{μικρό} = 0\) Για \(α > 70°\)
\({ντο}_{μικρό} = (70° – α)/40°\) Για \(30° < α ≤ 70°\)
Ειδικό βάρος χιονιού, \(γ\)
Το ειδικό βάρος του χιονιού καθορίζεται στο 4.1.6.13 και λαμβάνεται ως:
\(γ = 0.43{μικρό}_{μικρό} + 2.2 kN /{Μ}^{3} ≤ 4.0kN /{Μ}^{3}\) (4)
Για αυτό το παράδειγμα, \(γ\) είναι ίσο με \(2.673 kN /{Μ}^{3}\).
Συντελεστής συσσώρευσης, \({ντο}_{ένα}\)
Συντελεστής συσσώρευσης, \({ντο}_{ένα}\), υπολογίζεται ανάλογα με την περίπτωση φορτίου θεωρείται ως λεπτομερής στο 4.1.6.2 (8). Η τιμή αυτή θα υπολογιστεί αναλυτικά ανά περίπτωση.
Καθορισμένο φορτίο χιονιού, \(ΜΙΚΡΟ)
Σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ, το καθορισμένο φορτίο χιονιού, \(ΜΙΚΡΟ), θα υπολογιστεί για τις ισορροπημένες και παρασυρόμενες περιπτώσεις.
Ισορροπημένη / Μη αποσυμπιεζόμενη θήκη
Για την ισορροπημένη θήκη, ο συντελεστής συσσώρευσης \({ντο}_{ένα}\) είναι ίσο με 1.0. Εξάλλου, αφού η γωνία κλίσης της οροφής \(α\) είναι \(16°\) και η επιφάνεια της οροφής θεωρείται ότι είναι ανεμπόδιστη ολισθηρή, ο παράγοντας κλίσης, \({ντο}_{μικρό}\), για το παράδειγμα μας είναι ίσο με 0.978. Χρησιμοποιώντας εξίσωση (1), το καθορισμένο φορτίο χιονιού, \(ΜΙΚΡΟ), για ισορροπημένη / μη αποσυμπιεζόμενη θήκη είναι:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa
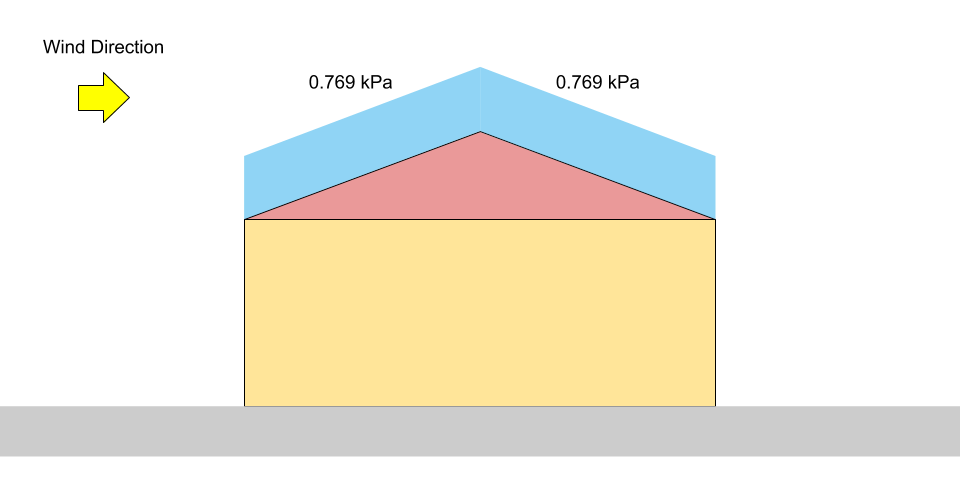
Φιγούρα 3: Διάγραμμα φόρτωσης για ισορροπημένο φορτίο χιονιού σε στέγη αετωμάτων.
Μη ισορροπημένη / παρασυρόμενη θήκη
Ο άνεμος ενεργεί κανονικά στην κορυφογραμμή
Δεδομένου ότι οι κατασκευές έχουν στέγες με αέτωμα, το μη ισορροπημένο φορτίο χιονιού (ο άνεμος ενεργεί κανονικά στην κορυφογραμμή) συντελεστής συσσώρευσης \({ντο}_{ένα}\) βρίσκεται χρησιμοποιώντας 4.1.6.9:
\({ντο}_{ένα, ανέβασμα} = 0\)
\({ντο}_{ένα, καταιγίδα} = 0.25 +α/20) Για \(15° ≤ α ≤ 20°\)
\({ντο}_{ένα, καταιγίδα} = 1.25\) Για \(20° < α ≤ 90°\)
Επειδή και οι δύο κατασκευές έχουν γωνία βήματος στέγης ίση με 16 °, τους παράγοντες συσσώρευσης \({ντο}_{ένα, ανέβασμα}\) και \({ντο}_{ένα, καταιγίδα}\) είναι ίσες με 0 και 1.05, αντίστοιχα. Εξάλλου, αφού η γωνία κλίσης της οροφής \(α\) είναι \(16°\) και η επιφάνεια της οροφής θεωρείται ότι είναι ανεμπόδιστη ολισθηρή, ο παράγοντας κλίσης, \({ντο}_{μικρό}\), για το παράδειγμα μας είναι ίσο με 0.978.
Στην μη ισορροπημένη / παρασυρόμενη θήκη κανονική στην κορυφογραμμή, \({ντο}_{ένα}\) υπολογίζεται βάσει 4.1.6.9 για θήκη οροφής με αέτωμα. Από τον παραπάνω υπολογισμό, \({ντο}_{ένα, ανέβασμα} = 0\) και \({ντο}_{ένα, καταιγίδα} = 1.05\). Ως εκ τούτου, τα καθορισμένα φορτία χιονιού για κάθε πλευρά είναι:
\({μικρό}_{ανέβασμα} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({Π}_{1}\)
\({μικρό}_{καταιγίδα} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({Π}_{2}\)
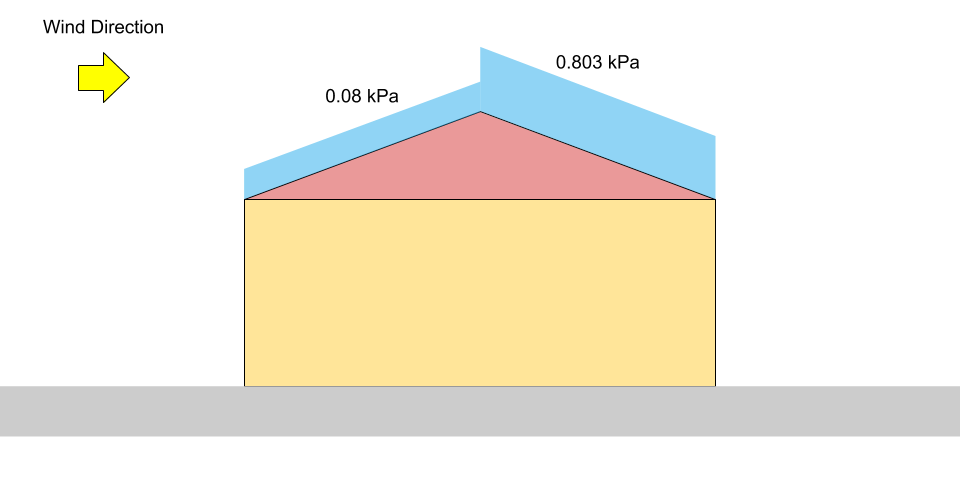
Φιγούρα 4: Διάγραμμα φόρτωσης για μη ισορροπημένο φορτίο χιονιού σε στέγη αετωμάτων (όχι σε κλίμακα).
Άνεμος που ενεργεί παράλληλα με την κορυφογραμμή – Περίπτωση I – Άνεμος από Άνω έως Κάτω Στέγη
Όταν ο άνεμος ενεργεί παράλληλα με την κορυφογραμμή, μια χιονοστιβάδα πιθανότατα θα αναπτυχθεί στην κάτω οροφή. Προκειμένου να καθοριστεί η συντελεστής συσσώρευσης \({ντο}_{ένα}\), οι ακόλουθοι τύποι από 4.1.6.2 (8) είναι μεταχειρισμένα:
\({ντο}_{ένα} ={ντο}_{α0} – ({ντο}_{α0} – 1)(Χ/{Χ}_{ρε})\) Για \(0 ≤ x ≤ {Χ}_{ρε}\)
\({ντο}_{ένα} = 1.0\) Για \(Χ > {Χ}_{ρε}\)
Οπου:
\({ντο}_{α0}\) = μέγιστη τιμή του \({ντο}_{α0}\) στο x = 0
\(Χ) = απόσταση από το βήμα της οροφής
\({Χ}_{ρε}\) = μήκος μετατόπισης όπως φαίνεται στο σχήμα 3 παρακάτω

Φιγούρα 5: Απεικόνιση παραμέτρων διάστασης οροφής

Φιγούρα 6: Αντίστοιχο φορτίο μετατόπισης στην κάτω οροφή με βάση Σχήμα 4.1.6.5-Α.
\({ντο}_{α0}\) και \({Χ}_{ρε}\) μπορεί να υπολογιστεί χρησιμοποιώντας τους ακόλουθους τύπους:
\({ντο}_{α0} = frac{βγh}{{ντο}_{σι}{μικρό}_{μικρό}}\) ή \({ντο}_{α0} = frac{φά}{{ντο}_{σι}}\) (5), όποιο είναι μικρότερο
\({Χ}_{ρε} = 5 \frac{{ντο}_{σι}{μικρό}_{μικρό}}{γ}({ντο}_{α0} – 1)\) (6)
\(F = 0,35β sqrt{\frac{γ({μεγάλο}_{cs} – 5{{η}_{Π}}^{«})}{{μικρό}_{μικρό}}} +{ντο}_{σι}\) αλλά \(F ≤ 5\) Για \({ντο}_{ws} = 1.0\) (7)
\({η}^{«} = η – \frac{{ντο}_{σι}{ντο}_{β}{μικρό}_{μικρό}}{γ}\) (8)
\({{η}_{Π}}^{«} ={η}_{Π} – \frac{0.8{μικρό}_{μικρό}}{γ}\) αλλά \(0 ≤ {{η}_{Π}}^{«} ≤ frac{{μεγάλο}_{cs}}{5}\) (9)
Οπου:
\({η}_{Π}\) = ύψος στηθαίου στην άνω οροφή (0 σε αυτήν την περίπτωση αφού δεν υπάρχει στηθαίο)
\(ω ) = διαφορά ύψους μεταξύ άνω και κάτω οροφής
\({ντο}_{ws}\) = τιμή του \({ντο}_{β}\) ισχύει για την πηγή παρασυρόμενων
\({μεγάλο}_{cs}\) = χαρακτηριστικό μήκος της περιοχής πηγής που ορίζεται ως: \(2{β}_{μικρό} -{{β}_{μικρό}}^{2}/{μεγάλο}_{μικρό}\)
\({μεγάλο}_{μικρό}\) = μεγαλύτερη διάσταση σχεδίου της περιοχής πηγής όπως φαίνεται στο σχήμα 7 και 8, Φαίνεται παρακάτω
\({β}_{μικρό}\) = μικρότερη διάσταση σχεδίου της περιοχής πηγής όπως φαίνεται στο σχήμα 7 και 8, Φαίνεται παρακάτω
\(β) = 1.0 για την υπόθεση I, και 0.67 για τις υποθέσεις II και III.
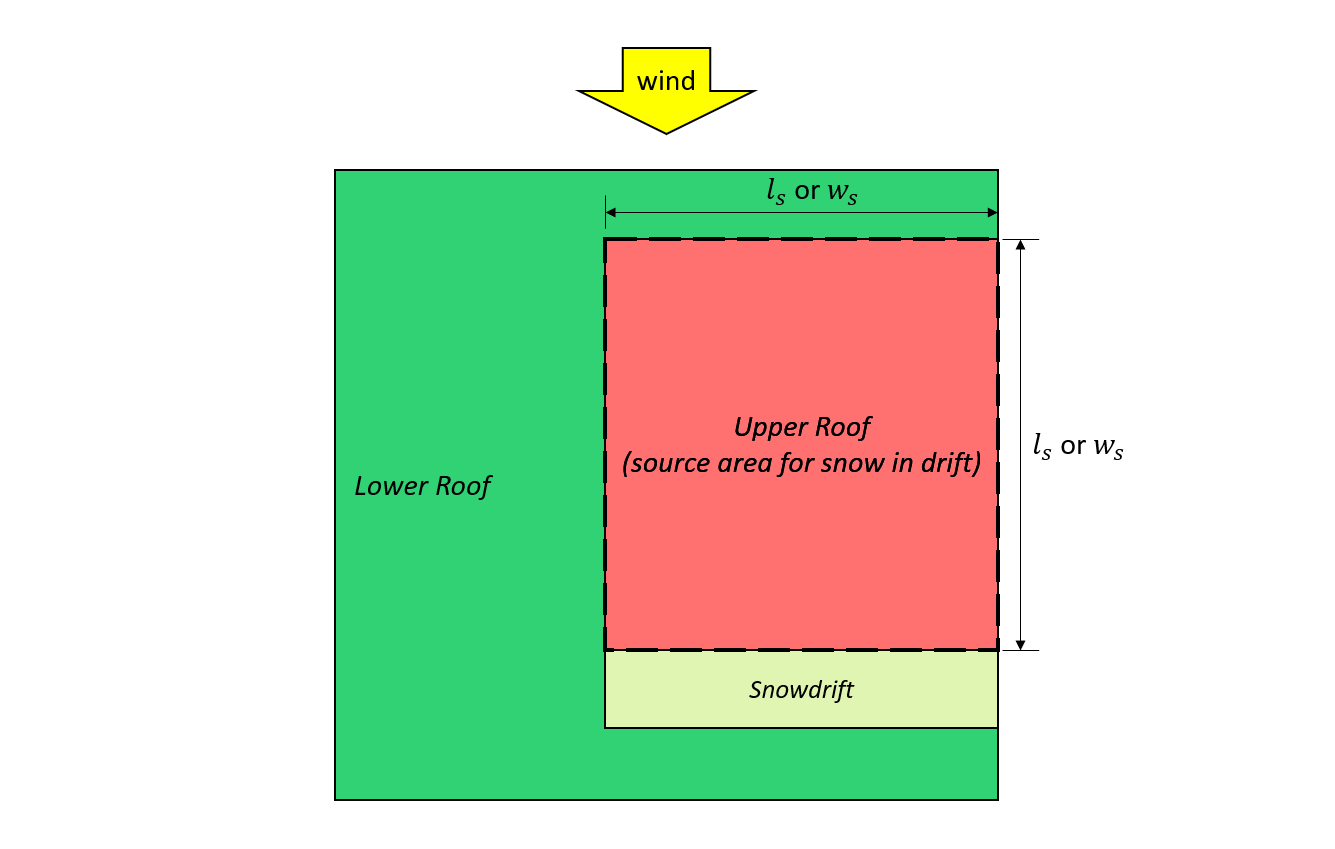
Φιγούρα 7: Περίπτωση I – χιονοστιβάδα σχηματίζεται από τον άνεμο που προέρχεται από την άνω οροφή με βάση Σχήμα 4.1.6.5-B.
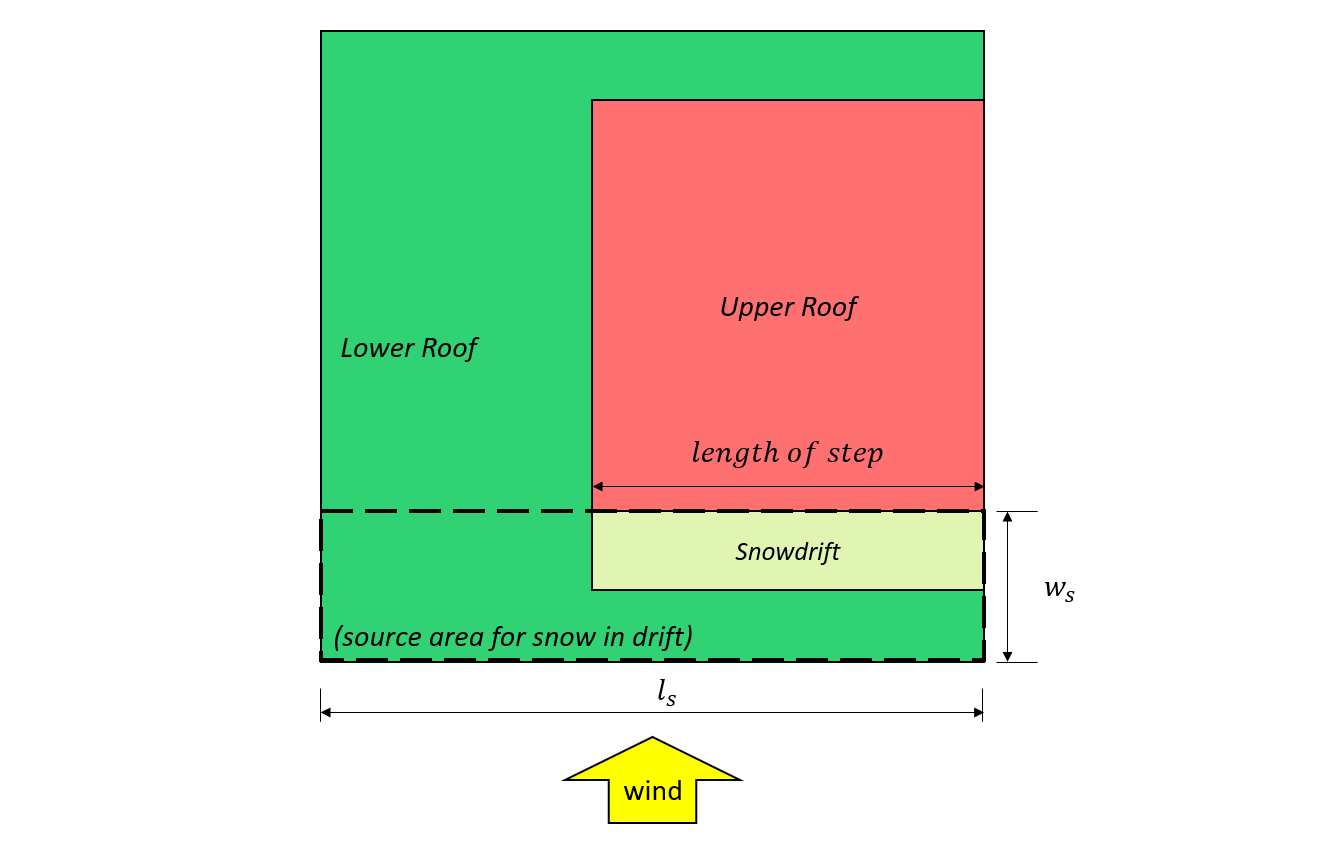
Φιγούρα 8: Περίπτωση II – χιονοστιβάδα σχηματίζεται από τον άνεμο που προέρχεται από την κάτω οροφή με βάση Σχήμα 4.1.6.5-B.
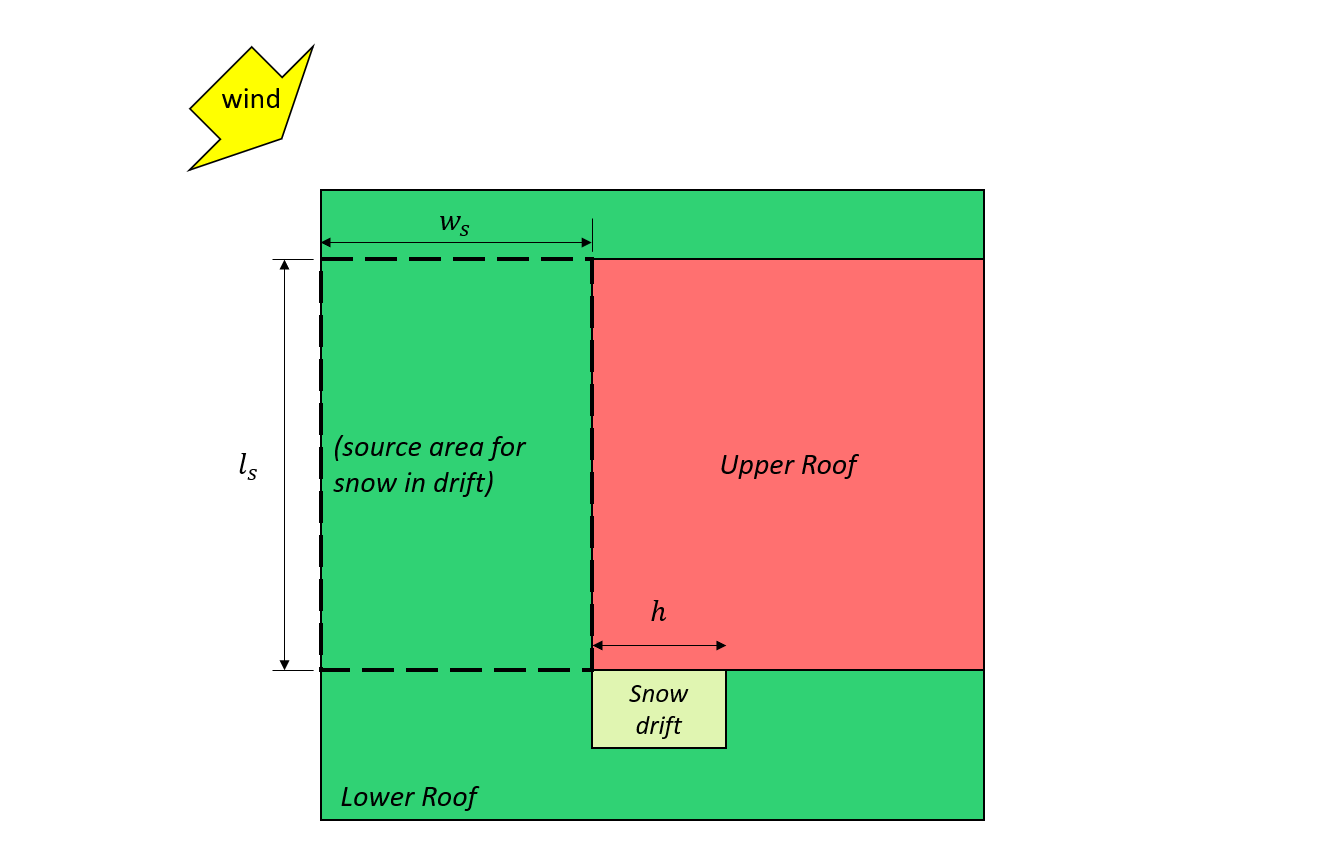
Φιγούρα 7: Περίπτωση III – μερική χιονοστιβάδα που σχηματίζεται από τον άνεμο που προέρχεται από την κάτω οροφή με βάση Σχήμα 4.1.6.5-B.
Για αυτό το παράδειγμα, Θα εξεταστούν οι περιπτώσεις I και II.
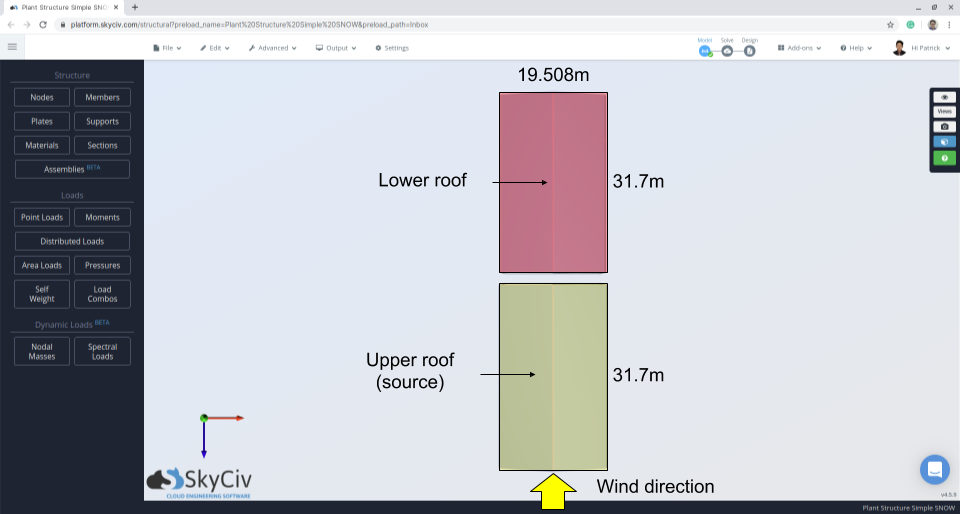
Φιγούρα 10: Σχέδιο δομής που δείχνει την κατεύθυνση του ανέμου και την περιοχή πηγής.
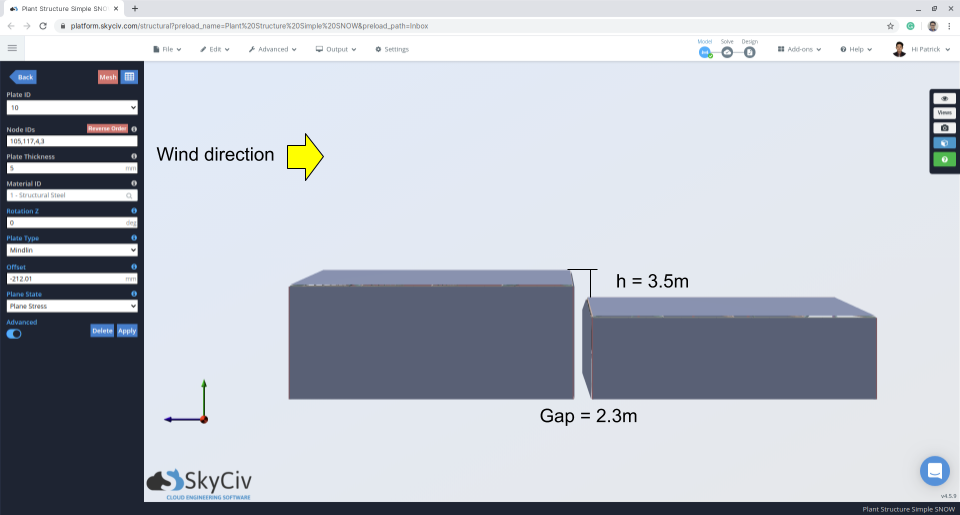
Φιγούρα 11: Προβολή ύψους που δείχνει το κενό και τη διαφορά της άνω και κάτω οροφής.
Για τη μη ισορροπημένη / παρασυρόμενη θήκη παράλληλη με την κορυφογραμμή, \({ντο}_{ένα}\) υπολογίζεται για την υπόθεση I και την περίπτωση II βάσει 4.1.6.5 για την οροφή πολλαπλών επιπέδων. Για την υπόθεση I, Αυτές οι ακόλουθες παράμετροι πρέπει πρώτα να υπολογιστούν χρησιμοποιώντας τις διάφορες εξισώσεις που αναφέρθηκαν προηγουμένως σε αυτό το παράδειγμα:
\(β = 1.0\)
\({η}^{«} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 Μ)
\({η}_{Π} = 0\)
\({{η}_{Π}}^{«} =0\)
\({μεγάλο}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 Μ)
\(F = 0.35(1.0)\τ.μ.{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({ντο}_{α0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) ή \({ντο}_{α0} = frac{3.66}{0.8} = 4.544\)
\({ντο}_{α0} = 4.544\)
\({Χ}_{ρε} = 5 \frac{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 Μ)
Από αυτές τις παραμέτρους, ο συντελεστής συσσώρευσης, \({ντο}_{ένα}\), μπορεί να υπολογιστεί αντικαθιστώντας την τιμή του \({ντο}_{α0}\) στο καθένα \(Χ) απόσταση. Λάβετε υπόψη ότι πρέπει να υπολογίσουμε \({ντο}_{ένα}\) στο \(x = a\) όπου \(a\) είναι το κενό μεταξύ της οροφής αφού το διάκενο οροφής είναι μικρότερο από 5 m όπως ορίζεται στο 4.1.6.6.
στο \(x = 0\): \({ντο}_{ένα} = 4.544 – (4.544 – 1)(0/5.835) = 4.544\)
στο \(x = a\): \({ντο}_{ένα} = 4.544 – (4.544 – 1)(2.3/5.835) = 3.147\)
στο \(x = {Χ}_{ρε}\): \({ντο}_{ένα} =1.0\)
στο \(x = 10{η}^{«}\): \({ντο}_{ένα} =1.0\)
Δεδομένου ότι το Η γωνία στέγης για αυτήν την περίπτωση είναι ίση με 0° σε αναφορά σε αυτή την ενότητα, \({ντο}_{μικρό} = 1.0\). Εξάλλου, κατά την εύρεση του καθορισμένου φορτίου χιονιού στην επάνω οροφή, ο συντελεστής συσσώρευσης, \({ντο}_{ένα}\), και παράγοντας κλίσης, \({ντο}_{μικρό}\), είναι και τα δύο 1.0. Ως εκ τούτου, το μέγεθος των καθορισμένων φορτίων χιονιού σε κάθε τοποθεσία είναι:
στο \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa )
στο \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {Π}_{1}\)
στο \(x = {Χ}_{ρε}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={Π}_{2} = {Π}_{3}\)
σε ανώτερο επίπεδο οροφής: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa )
Άνεμος που ενεργεί παράλληλα με την κορυφογραμμή – Περίπτωση II – Άνεμος από Κάτω έως Άνω Στέγη
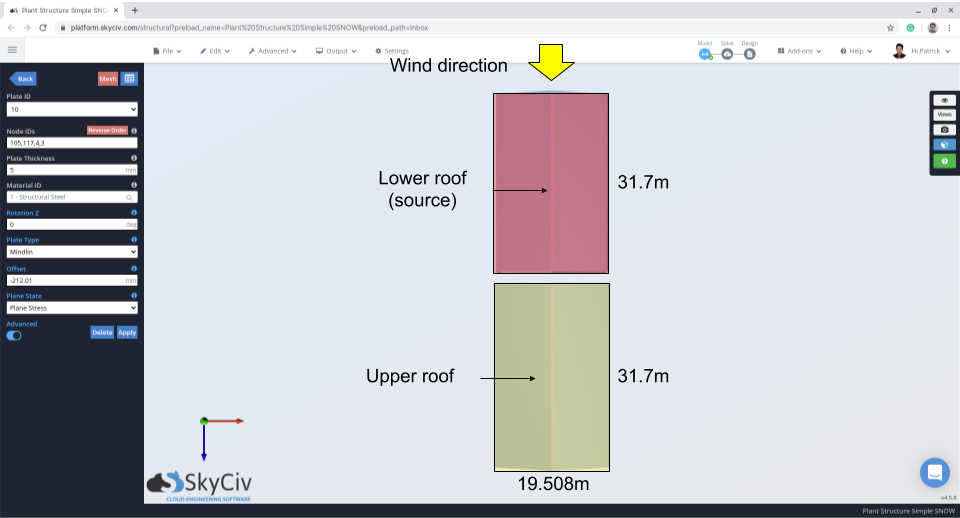
Φιγούρα 12: Σχέδιο δομής που δείχνει την κατεύθυνση του ανέμου και την περιοχή πηγής – άνεμος από κάτω στέγη προς τα πάνω.
Για την υπόθεση II, ο υπολογισμός είναι παρόμοιος με την περίπτωση Ι, αλλά έχει διαφορετικό \(β = 0.67\):
\(β = 0.67\)
\({η}^{«} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 Μ)
\({η}_{Π} = 0\)
\({{η}_{Π}}^{«} =0\)
\({μεγάλο}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 Μ)
\(F = 0.35(0.67)\τ.μ.{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({ντο}_{α0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) ή \({ντο}_{α0} = frac{2.70}{0.8} = 3.375\)
\({ντο}_{α0} = 3.375\)
\({Χ}_{ρε} = 5 \frac{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 Μ)
στο \(x = 0\): \({ντο}_{ένα} = 3.375 – (3.375 – 1)(0/3.909) = 3.375\)
στο \(x = a\): \({ντο}_{ένα} = 3.375 – (3.375 – 1)(2.3/3.909) = 1.978\)
στο \(x = {Χ}_{ρε}\): \({ντο}_{ένα} =1.0\)
στο \(x = 10{η}^{«}\): \({ντο}_{ένα} =1.0\)
στο \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa )
στο \(x = a\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {Π}_{1}\)
στο \(x = {Χ}_{ρε}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {Π}_{2} = {Π}_{3}\)
σε ανώτερο επίπεδο οροφής: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa )
Για απεικόνιση, το αντίστοιχο \({Π}_{1}\), \({Π}_{2}\), και \({Π}_{3}\) φαίνονται στα σχήματα 13 και 14 παρακάτω και για τις δύο υποθέσεις I και II, αντίστοιχα.
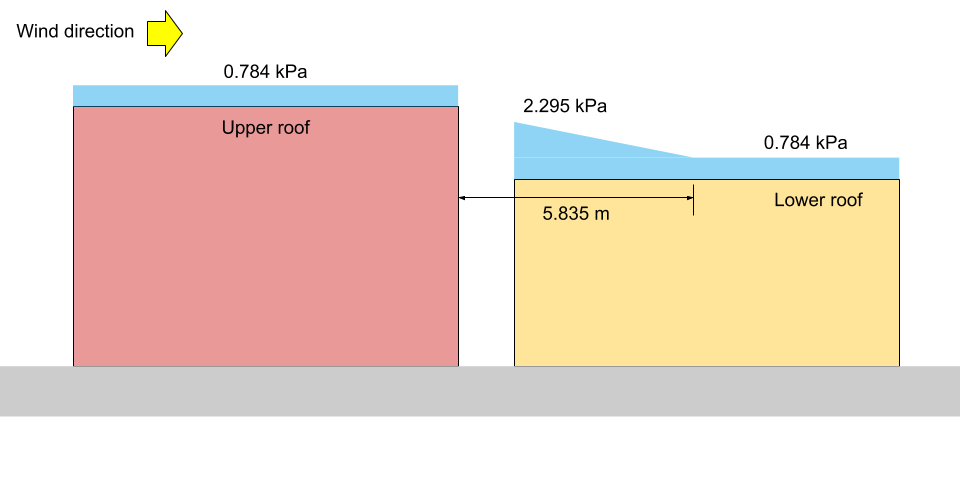
Φιγούρα 13: Εικόνα φορτίου χιονιού για την περίπτωση I (όχι σε κλίμακα).
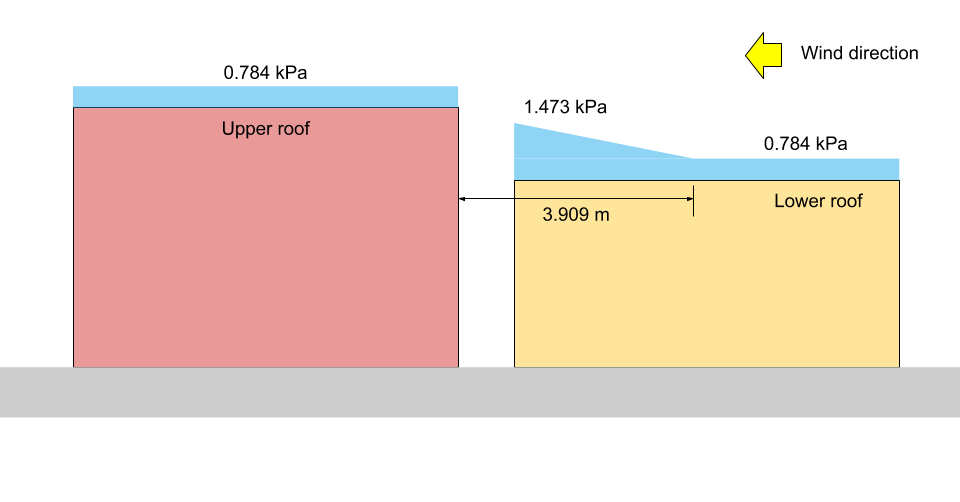
Φιγούρα 14: Εικόνα φορτίου χιονιού για την περίπτωση II (όχι σε κλίμακα).
Ολοκληρώστε αυτούς τους υπολογισμούς αυτόματα σε λίγα λεπτά
Αυτός ήταν ένας μακρύς υπολογισμός, τι μπορείτε να κάνετε ως μηχανικός για να επιταχύνετε αυτήν τη διαδικασία για τα μελλοντικά σας έργα? Πρόσφατα το SkyCiv κυκλοφόρησε και αυτοματοποίησε το Snow Load Generator ως μέρος του SkyCiv Load Generator, που μπορεί επίσης να δημιουργήσει φορτία ανέμου. Για να βρείτε τα φορτία χιονιού του παραδείγματος που εμφανίζεται, χρειάζονται μόνο μερικά κλικ χρησιμοποιώντας το εργαλείο:
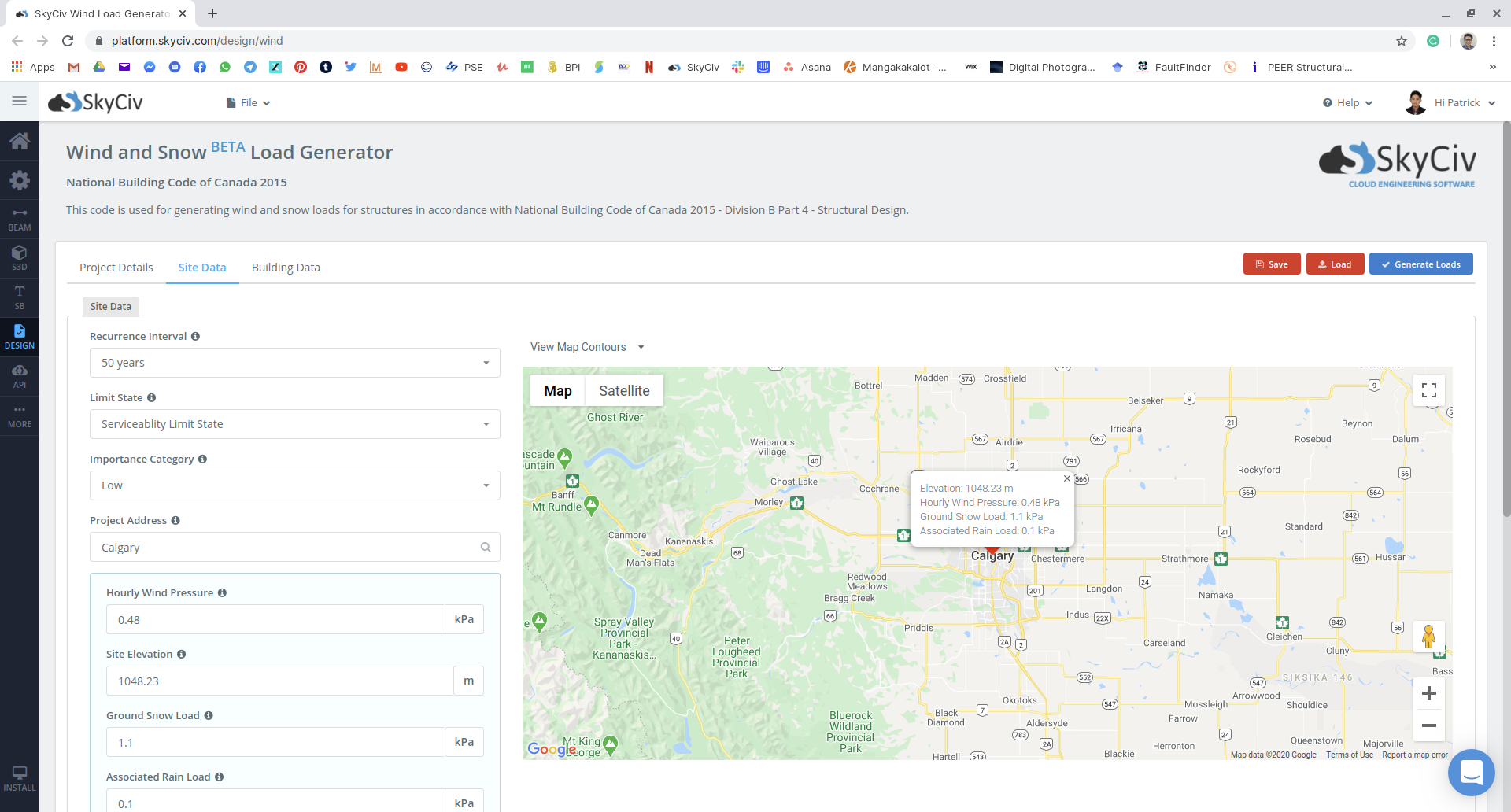
Φιγούρα 15: Εισαγωγή δεδομένων ιστότοπου στην ενότητα SkyCiv Load Generator χρησιμοποιώντας το παράδειγμά μας.
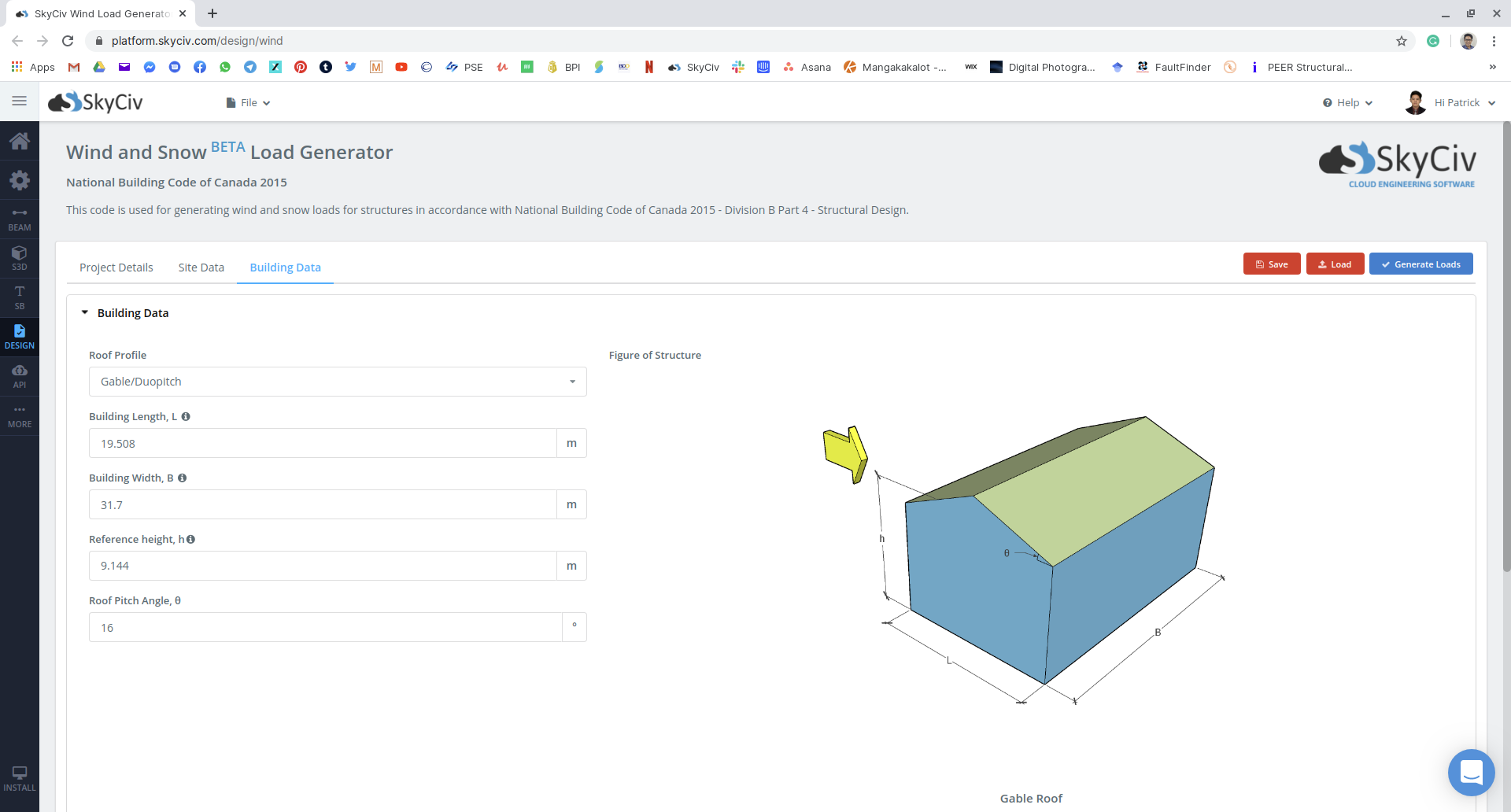
Φιγούρα 16: Εισαγωγή παραμέτρων δημιουργίας και χιονιού στην ενότητα SkyCiv Load Generator χρησιμοποιώντας το παράδειγμά μας.
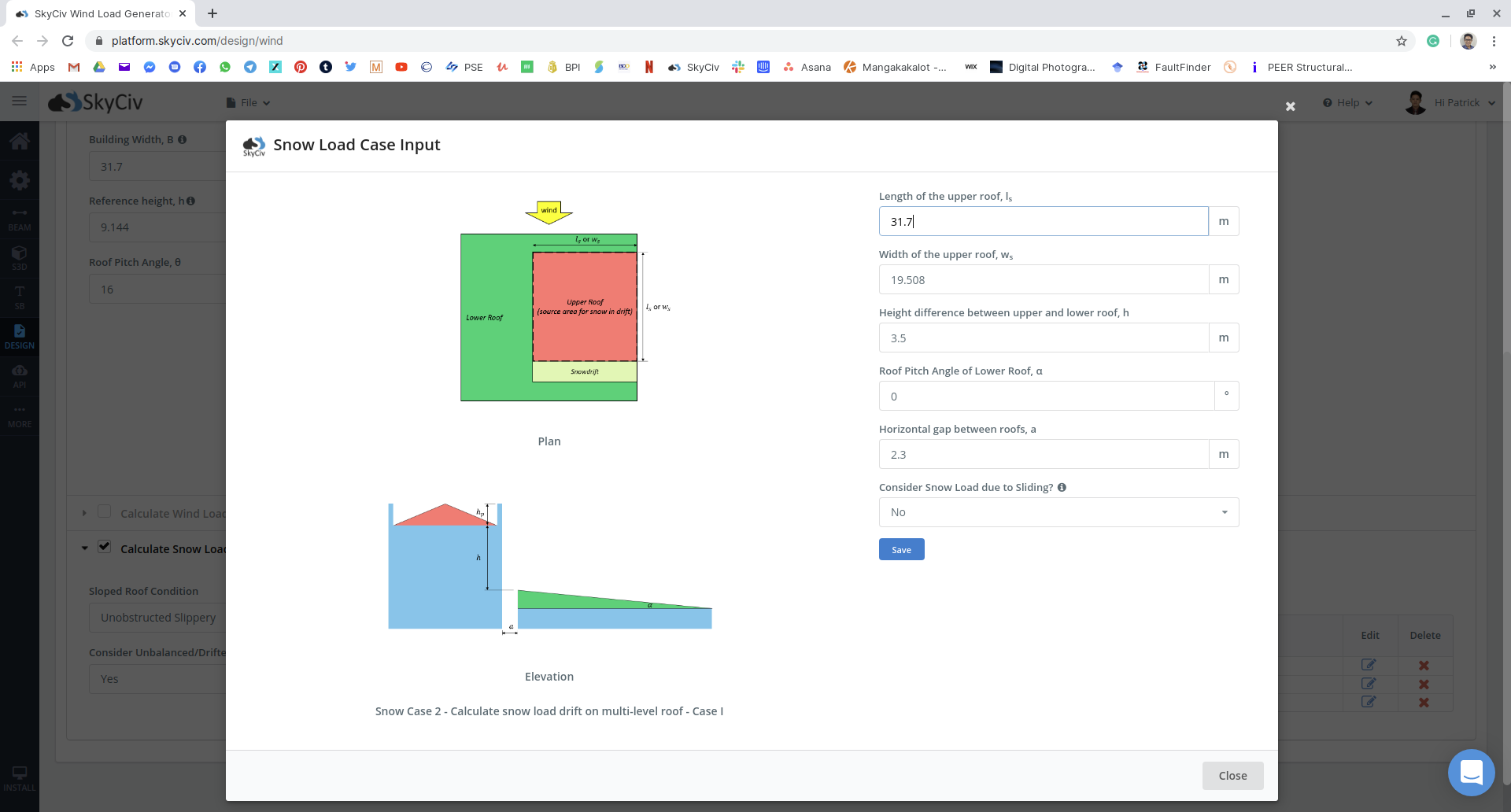
Φιγούρα 17: Είσοδος φορτίου χιονιού για πολλές μη ισορροπημένες περιπτώσεις για το παράδειγμα.
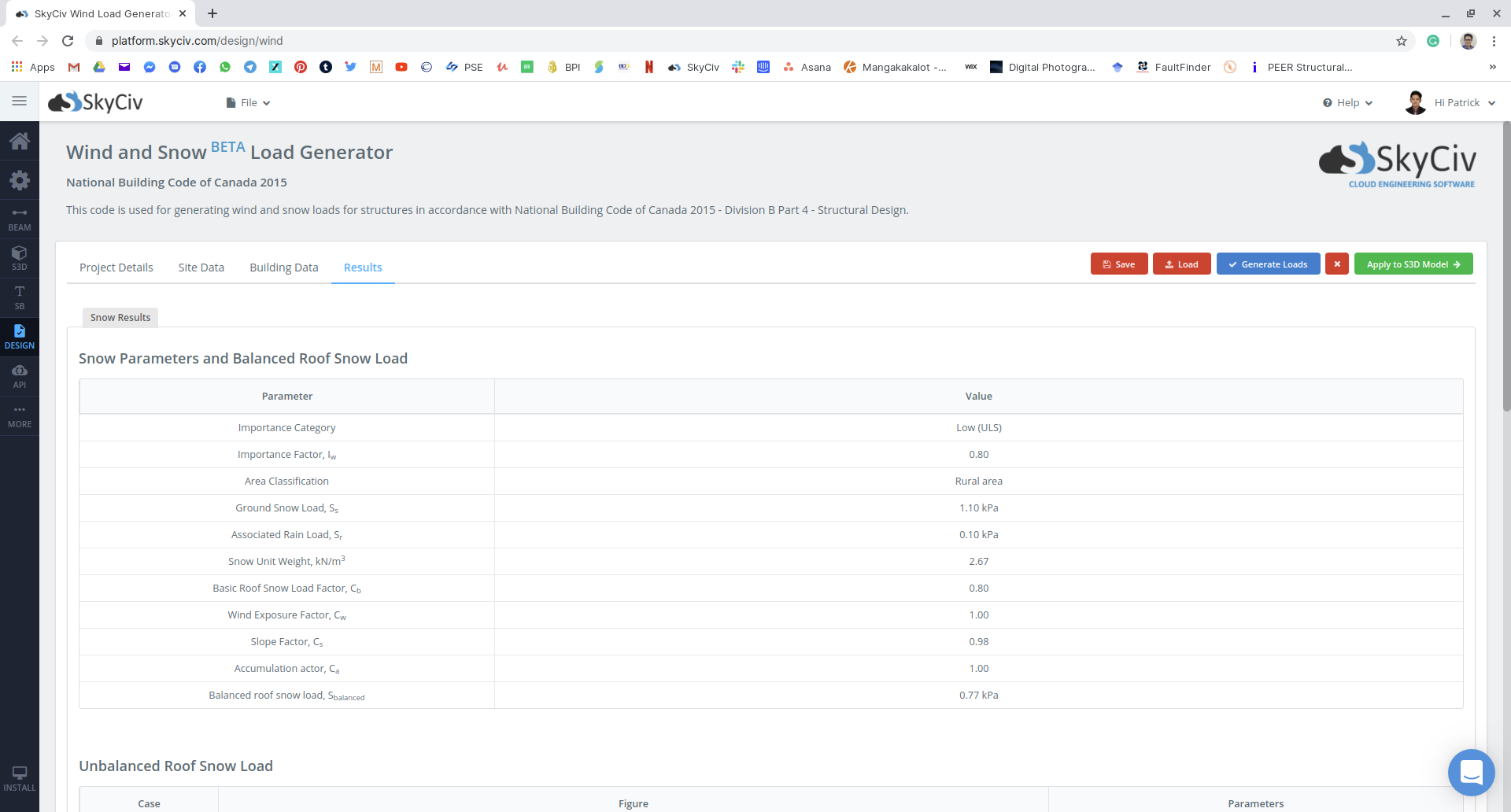
Φιγούρα 18: Περίληψη των παραμέτρων φορτίου χιονιού που χρησιμοποιήθηκαν και του ισορροπημένου φορτίου χιονιού που θα εφαρμοστεί στη δομή.
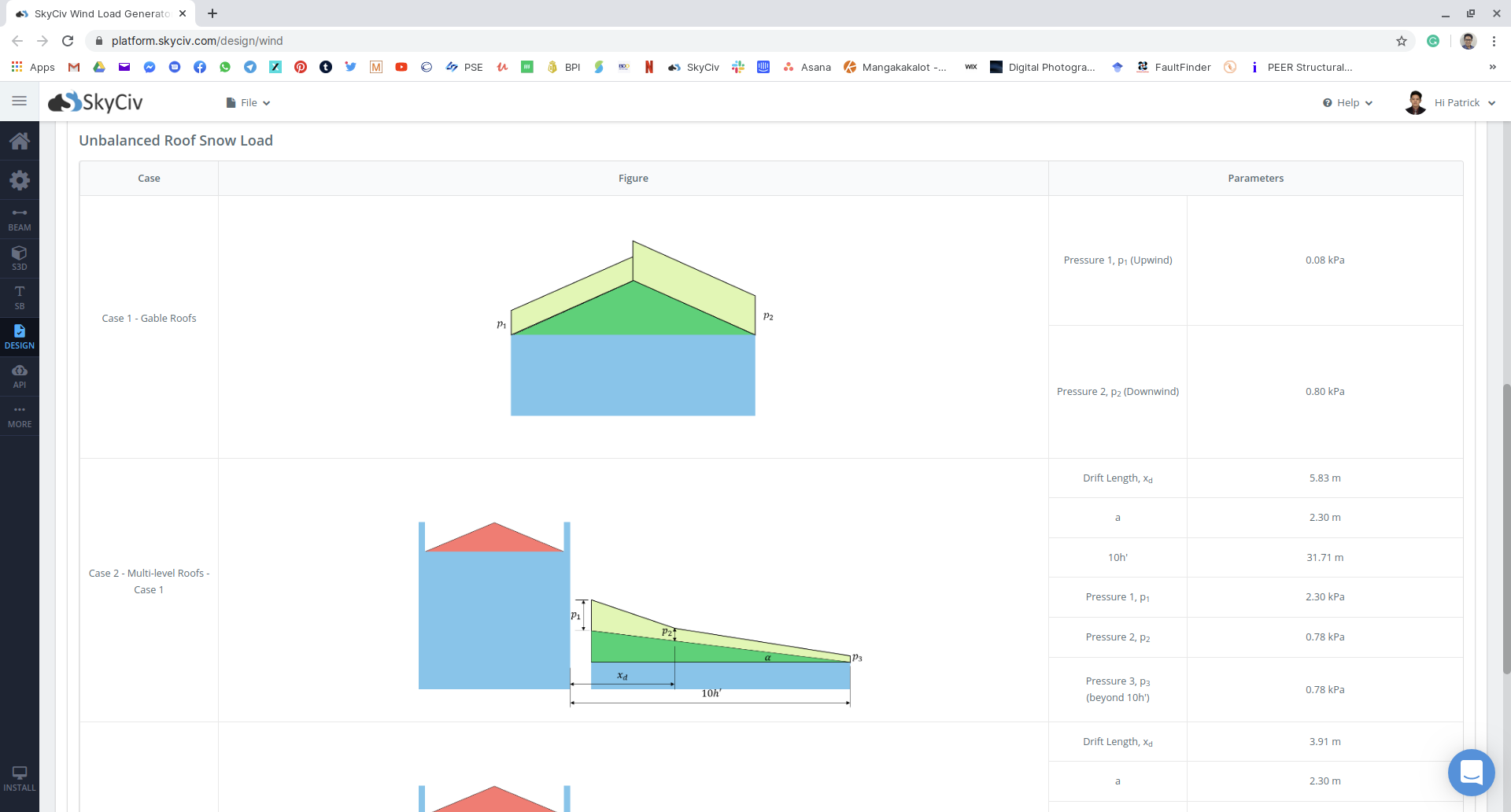
Φιγούρα 19: Σύνοψη των μη ισορροπημένων αποτελεσμάτων φορτίου χιονιού.
Οι υπολογισμοί φορτίου χιονιού στη μονάδα SkyCiv Load Generator υποστηρίζονται από κωδικούς αναφοράς όπως το ASCE 7-10, 7-16, ΣΕ 1991-1-3, NBCC 2015, και AS / NZS 1170.3, και είναι διαθέσιμο στο Αυτόνομο (Φόρτωση μόνο γεννήτριας) και Επαγγελματίας λογαριασμοί. Εξοικειωμένοι με τον προγραμματισμό και τα API? Αυτή η λειτουργικότητα μπορεί να αυτοματοποιηθεί με τη χρήση του API SkyCiv.
Δομικός μηχανικός, Ανάπτυξη προϊόντων
MS Πολιτικών Μηχανικών
βιβλιογραφικές αναφορές:
- Εθνικό Συμβούλιο Έρευνας του Καναδά. (2015). Εθνικός Κώδικας του Καναδά, 2015. Εθνικό Συμβούλιο Έρευνας του Καναδά.
Σημείωση:
- Αναφορά κωδικού NBCC για το “Βασικός συντελεστής φορτίου χιονιού οροφής” — ψάχνω 4.1.6.2 Πρόταση (2)
- Αναφορά κωδικού NBCC για το “Συντελεστής έκθεσης ανέμου” — ψάχνω 4.1.6.2 Καταδίκες (3) και (4)
- Αναφορά κωδικού NBCC για το “Παράγοντας κλίσης” — ψάχνω 4.1.6.2 Καταδίκες (5), (6), και (7)
- Αναφορά κωδικού NBCC για το “Συντελεστής συσσώρευσης” — ψάχνω 4.1.6.2 Πρόταση (8), 4.1.6.5 για στέγες πολλαπλών επιπέδων, 4.1.6.6 για στέγες με κενό, και 4.1.6.9 για στέγες με αέτωμα



