Συστήματα πλακών που θεωρούνται από το πρότυπο
Τα Αυστραλιανά Πρότυπα καθορίζουν τις ελάχιστες απαιτήσεις για το σχεδιασμό πλακών από οπλισμένο σκυρόδεμα, όπως μονόδρομοι και αμφίδρομοι τύποι. Σχετικά με τη διαμόρφωση κάτοψης και τη συμπερίληψη δοκών, οι πλάκες μπορούν επίσης να χωριστούν σε πλάκες που στηρίζονται σε τέσσερις πλευρές, συστήματα δοκών και πλακών, επίπεδες πλάκες, και επίπεδες πλάκες. Αυτοί οι τύποι συνοψίζονται στις παρακάτω εικόνες.
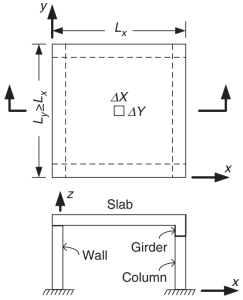
Φιγούρα 1. Πλάκα στηριγμένη σε τέσσερις πλευρές. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press).
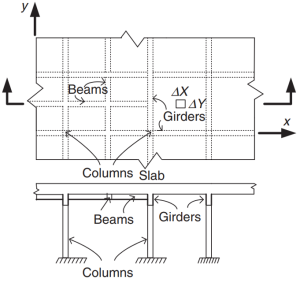
Φιγούρα 2. Σύστημα πλακών Grillage. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press).
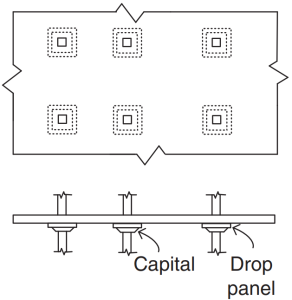
Φιγούρα 3. Επίπεδες Πλάκες. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press).
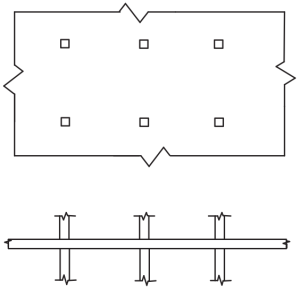
Φιγούρα 4. Επίπεδες πλάκες. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press).
Το Πρότυπο συνιστά ορισμένες μεθόδους (απλοποιημένες και αποδεδειγμένες διαδικασίες) στον προσδιορισμό των ροπών κάμψης:
- Ρήτρα 6.10.2: Συνεχείς δοκοί και πλάκες μονής κατεύθυνσης
- Ρήτρα 6.10.3: Πλάκες διπλής κατεύθυνσης που στηρίζονται σε τέσσερις πλευρές
- Ρήτρα 6.10.4: Πλάκες διπλής κατεύθυνσης με πολλαπλά ανοίγματα
Ο σκοπός του κώδικα είναι να σχεδιάσει τη συνολική ποσότητα οπλισμού από χάλυβα οπλισμού στις κύριες κατευθύνσεις στο σύστημα πλακών. Ο χάλυβας οπλισμού θα υπολογιστεί για τις ροπές κάμψης “Μx” και “Μου.” Φιγούρα 5 δείχνει τις άλλες δυνάμεις ή ενέργειες σε ένα πεπερασμένο στοιχείο πλάκας στο οποίο ο κώδικας ορίζει τις τιμές αντίστασής τους.
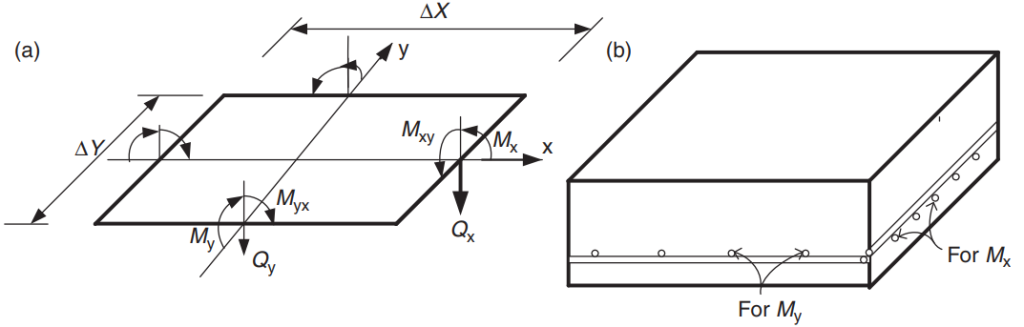
Φιγούρα 5. Δυνάμεις σε πεπερασμένο στοιχείο πλάκας: στιγμές κάμψης (Μx, Καμπύλες Mz-My και καμπύλες F-M), στιγμιότυπα (Mxy, Myx), και ψαλίδια (Qx, Qy). (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press)
Σε αυτό το άρθρο, θα αναπτύξουμε δύο παραδείγματα σχεδίασης πλακών, μονόδρομα και αμφίδρομα συστήματα πλακών, χρησιμοποιώντας τις απλουστευμένες μεθόδους που προσανατολίζονται και επιτρέπονται από τον κώδικα. Και στις δύο περιπτώσεις, θα δημιουργήσουμε ένα μοντέλο SkyCiv S3D και θα συγκρίνουμε τα αποτελέσματα με τις μεθόδους που αναφέρονται παραπάνω.
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
Παράδειγμα σχεδίασης πλάκας μονής κατεύθυνσης
Παρακάτω φαίνεται το μικρό κτίριο και οι πλάκες που θα σχεδιάσουμε
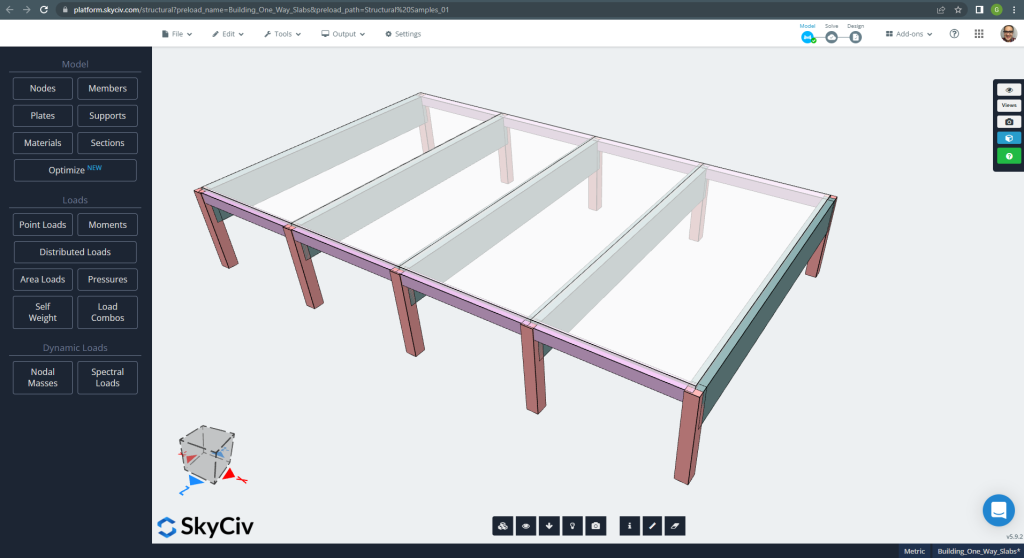
Φιγούρα 6. Μονόδρομες πλάκες σε ένα μικρό παράδειγμα κτιρίου. (Δομικά 3D, SkyCiv Cloud Engineering).
Οι διαστάσεις του σχεδίου φαίνονται στη συνέχεια
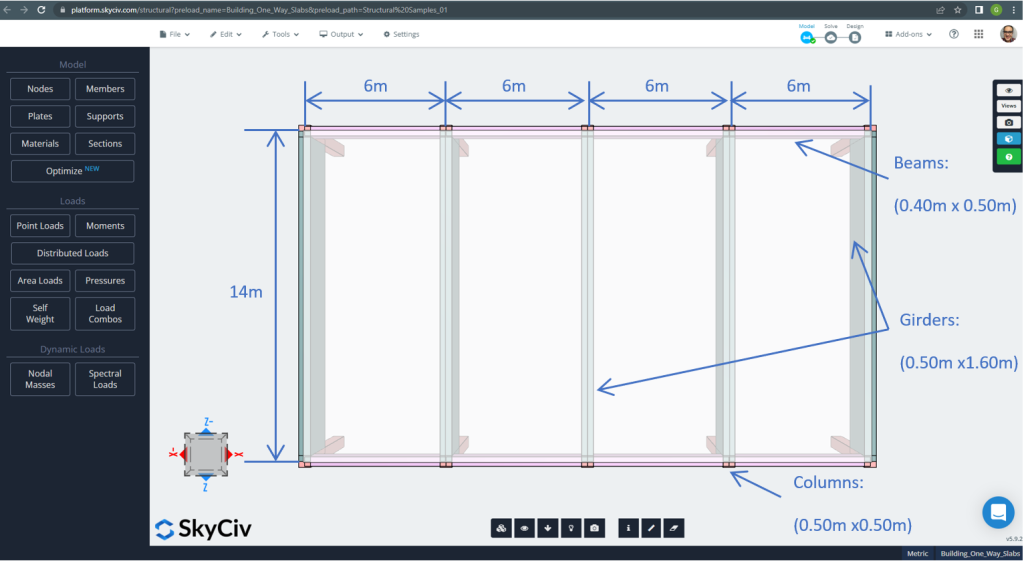
Φιγούρα 7. Διαστάσεις σχεδίου και δομικά στοιχεία. (Δομικά 3D, SkyCiv Cloud Engineering).
Για το παράδειγμα πλάκας, Συνοψίζοντας, το υλικό, ιδιότητες στοιχείων, και φορτία που πρέπει να ληφθούν υπόψη :
- Ταξινόμηση τύπου πλάκας: Ενας – τρόπο συμπεριφοράς \(\frac{L_2}{L_1} > 2 ; \frac{14Μ}{6Μ}=2,33 > 2.00 \) Εντάξει!
- Επάγγελμα κτιρίου: Οικιστική χρήση
- Πάχος πλάκας \(αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{πλάκα}=0,25m)
- Πυκνότητα οπλισμένου σκυροδέματος υποθέτοντας αναλογία οπλισμού χάλυβα ίση με 0.5% \(\rho_w = 24 \frac{ΚΝ}{m^3} + 0.6 \frac{ΚΝ}{m^3} \φορές 0.5 = 24.3 \frac{ΚΝ}{m^3} \)
- Χαρακτηριστική θλιπτική αντοχή σκυροδέματος στο 28 μέρες \(f’c = 25 MPa \)
- Concrete Modulus of Elasticity by Australian Standard \(E_c = 26700 MPa \)
- Πλάκα Αυτο-βάρος \(Νεκρό = rho_w φορές t_{πλάκα} = 24.3 \frac{ΚΝ}{m^3} \φορές 0,25m = 6.075 \frac {ΚΝ}{m^2}\)
- Υπερ-επιβεβλημένο νεκρό φορτίο \(SD = 3.0 \frac {ΚΝ}{m^2}\)
- Ζωντανό φορτίο \(L = 2.0 \frac {ΚΝ}{m^2}\)
Υπολογισμός με το χέρι σύμφωνα με το Πρότυπο AS3600
Σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ, θα υπολογίσουμε την απαιτούμενη ράβδο από ενισχυμένο χάλυβα χρησιμοποιώντας την αναφορά του Αυστραλιανού Προτύπου. Λαμβάνουμε πρώτα τη συνολική συντελεστή ροπής κάμψης που πρέπει να πραγματοποιηθεί από τη λωρίδα ενιαίου πλάτους της πλάκας.
- Νεκρό φορτίο, \(g = (3.0 + 6.075) \frac{ΚΝ}{m^2} \φορές 1 m = 9.075 \frac{ΚΝ}{Μ}\)
- Ζωντανό φορτίο, \(q = (2.0) \frac{ΚΝ}{m^2} \φορές 1 m = 2.0 \frac{ΚΝ}{Μ}\)
- Απόλυτο φορτίο, \(Fd = 1,2 φορές g + 1.5\φορές q = (1.2\φορές 9.075 + 1.5\φορές 2.0)\frac{ΚΝ}{Μ} =13,89 φράκ{ΚΝ}{Μ} \)
Χρησιμοποιώντας την απλοποιημένη μέθοδο που καθορίζεται από το πρότυπο, πρώτα, είναι απαραίτητο να συμμορφώνεστε με τους ακόλουθους περιορισμούς:
- \(\frac{L_i}{L_j} \ο 1.2 . \frac{6Μ}{6Μ} =1 < 1.2 \). Εντάξει!
- Το φορτίο πρέπει να είναι ομοιόμορφο. Εντάξει!
- \(q le 2g. q=2 frac{ΚΝ}{Μ} < 18.15 \frac{ΚΝ}{Μ}\). Εντάξει!
- Η διατομή της πλάκας πρέπει να είναι ομοιόμορφη. Εντάξει!.
Συνιστώμενο ελάχιστο πάχος, ρε
\(d ge frac{ΜΕΓΑΛΟ_{Φε}}{{k_3}{k_4}{\τ.μ.[3]{\frac{\frac{\Δέλτα}{ΜΕΓΑΛΟ_{εφ}}{E_c}}{ΦΑ_{ρε, εφ}}}}}\)
Οπου
- \(k_3 = 1.0; k_4 = 1.75 \)
- \(\frac{\Δέλτα}{ΜΕΓΑΛΟ_{εφ}}=1/250 \)
- \(E_c = 27600 MPa \)
- \(ΦΑ_{ρε,εφ} = (1.0 +κ_{cs})\φορές g + (\psi_s + κ_{cs}\times psi_1) \φορές q=(1.0+0.8)\φορές 9.075 + (0.7+0.8\φορές 0.4)\φορές 2 = 18.375 kPa )
- \(\psi_s = 0.7 \) Βραχυπρόθεσμος παράγοντας ζωντανού φορτίου
- \(\psi_1 = 0.4 \) Μακροπρόθεσμος παράγοντας ζωντανού φορτίου
- \(κ_{cs} = 0.8 \)
\(d ge frac{5.50Μ}{{1.0}\φορές {1.75}{\τ.μ.[3]{\frac{\frac{1}{250}\φορές{27600 \φορές 10^3 kPa}}{18.375 kPa}}}} \ge 0,173μ. d = 0,25μ > 0.173Μ \) Εντάξει!
Μόλις δείξουμε ότι οι περιορισμοί ικανοποιούνται, η ροπή κάμψης υπολογίζεται χρησιμοποιώντας την έκφραση: \(M=alpha times F_d times L_n^2) όπου \(\alpha\) είναι μια σταθερά που ορίζεται στο παρακάτω σχήμα.
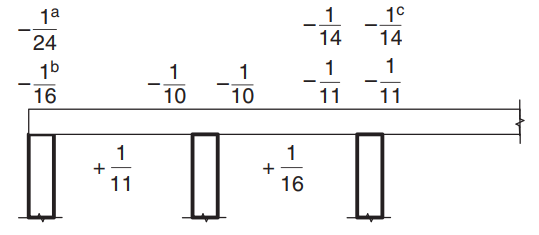
Φιγούρα 8. Τιμές συντελεστή ροπής \(\alpha\) για πλάκες με περισσότερα από δύο ανοίγματα. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press).
Οπου:
- (ένα) Θήκη πλακών και δοκών στη στήριξη δοκών
- (σι) Μόνο για συνεχή στήριξη δέσμης
- (ντο) Όπου χρησιμοποιείται οπλισμός κατηγορίας L
- \(L_n \) είναι το ενιαίο άνοιγμα της λωρίδας
- \(F_d \) είναι το βαρυτικό συντελεστή φορτίο
Για το παράδειγμα πλάκας, πρέπει να χρησιμοποιήσουμε περίπτωση (ένα) γιατί η πλάκα στηρίζεται σε άκαμπτες δοκούς. Θα εξηγηθεί μόνο μία περίπτωση και τα υπόλοιπα θα φανούν στον παρακάτω πίνακα. Περιλαμβάνουμε επίσης τον υπολογισμό της επιφάνειας του οπλισμού χάλυβα.
- \(Μ={\άλφα} {F_d}{L_n^2}={-\frac{1}{24}}\φορές {13.89 \frac{ΚΝ}{Μ}}\φορές (6Μ-0.5Μ)💕⬛ Αγορά Indocin από – 17.51{ΚΝ}{Μ}\)
- Κάλυμμα = 20mm (Απαιτούνται τουλάχιστον 10 mm για περίοδο πυραντοχής 60 λεπτά).
- \(d = t_{πλάκα} – Κάλυμμα – \frac{Διάμετρος Μπαρ}{2} = 250 mm – 20χιλ – 6mm = 224 mm \)
- \(\άλφα_2 = 1.0-0.003 f’c = 1,0-0,003φορές 25 = 0.925 (0.67 \το alpha_2 le 0.85) \) Ετσι, επιλέγουμε \(\άλφα_2 = 0.85\)
- \(\xi = frac{\άλφα_2 φορές f’c}{φά_{του}} = frac{0.85\φορές 25 MPa}{500 MPa} = 0.0425 \)
- \(\rho_t = xi – \τ.μ.{{\xi}^ 2 – \frac{{2}{\xi}{Μ}}{{\phi}{σι}{d^2}{φά_{του}}}} = 0.0425 – \τ.μ.{{0.0425}^2-φράκ{2\φορές 0,0425 φορές 17.51{ΚΝ}{Μ}}{{0.8}\φορές {1Μ}\φορές {{(0.224Μ)^ 2}} \φορές {500\φορές {10^ 3}kPa}}}=0,0008814)
- \(\γάμμα= 1.05-0.007 f’c = 1.05-0.007\times 25 = 0.875 (0.67 \le \gamma \le 0.85) \) Ετσι, επιλέγουμε \(\γάμμα = 0.85\)
- \(k_u = \frac{\rho_t \times f_{του}}{0.85\times \gamma \times f’c}= frac{0.0008814\φορές 500 MPa}{0.85\φορές 0.85 \φορές 25 MPa} =0.0244\)
- \(\φι = 1.19 – \frac{13\φορές k_{u0}}{12} = 1.19 – \frac{13\φορές 0.0244}{12} = 1.164 (0.6 \le \phi \le 0.8) \) Ετσι, επιλέγουμε \(\φι = 0.8\). Εντάξει!.
- \(\Οι ροπές κάμψης υπολογίζονται σε κάθε κατεύθυνση σε τμήματα{τ,ελάχ} = 0.20 {(\frac{ρε}{ρε})^ 2}{(\frac{φά'_{ct,φά}}{φά_{του}})} = 0.20 \φορές (\frac{0.25Μ}{0.224Μ})^2 \times \frac{0.6\φορές sqrt{25MPa}}{500 MPa} = 0.0015\)
- \(ΕΝΑ_{αγ}=μέγ(\Οι ροπές κάμψης υπολογίζονται σε κάθε κατεύθυνση σε τμήματα{τ,ελάχ}, \rho_t)\times b \times d = max(0.0015,0.0008814)\φορές 1000 mm \times 224 mm = 334.82 mm^2 \)
| \(\alpha\) και Στιγμές | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| \(\alpha\) αξία | -\(\frac{1}{24}\) | \(\frac{1}{11}\) | -\(\frac{1}{10}\) | \(\frac{1}{10}\) | \(\frac{1}{16}\) | \(\frac{1}{11}\) |
| Τιμή M | -17.51 | 38.20 | -42.02 | 42.02 | 26.26 | 38.20 |
| \(\rho_t\) | 0.0008814 | 0.001948 | 0.002148 | 0.002148 | 0.00133 | 0.001948 |
| προς την | 0.0244 | 0.0539 | 0.0594 | 0.0594 | 0.0368 | 0.05391 |
| \(\φι) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(ΕΝΑ_{αγ} {mm^2}\) | 334.82 | 436.31 | 481.099 | 481.099 | 334.8214 | 436.3100 |
Μετά τον υπολογισμό της επιφάνειας του χαλύβδινου οπλισμού, μπορείτε να ορίσετε τις λεπτομέρειες (ο πραγματικός τρόπος τοποθέτησης του οπλισμού στην πλάκα). Ως βοήθεια για τη γνώση σας, κοινοποιούμε την παρακάτω εικόνα, που υποδεικνύει τη θέση του οπλισμού για θετικές και αρνητικές στιγμές:
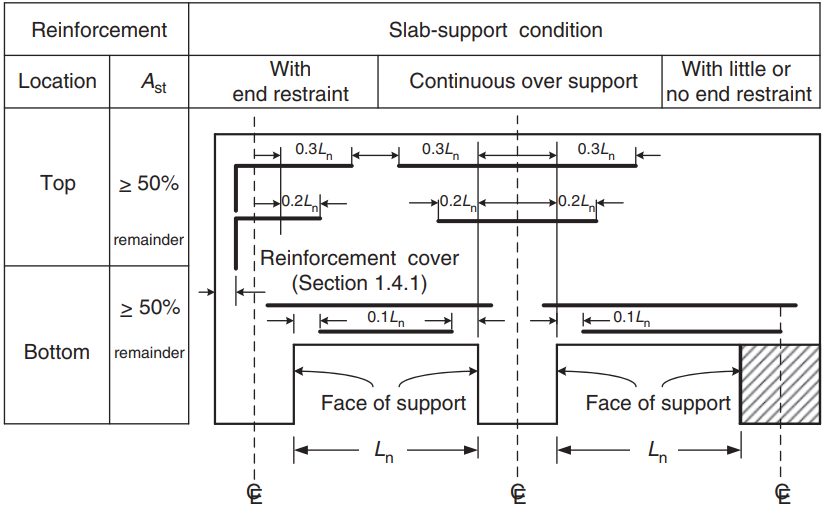
Φιγούρα 9. Ενίσχυση για πλάκες μονής και διπλής κατεύθυνσης. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press)
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
Αποτελέσματα ενότητας σχεδίασης πλακών SkyCiv S3D
Στην πρώτη άποψη, θα δείξουμε μερικές εικόνες για τη μοντελοποίηση και τη δομική ανάλυση του παραδείγματος στο S3D. Σας συνιστούμε να διαβάσετε για τη μοντελοποίηση στο SkyCiv στους παρακάτω συνδέσμους Πώς να μοντελοποιήσετε πιάτα? Ο πίνακας υλικών συμπληρώνεται αυτόματα από το Παράδειγμα σχεδίασης πλακών ACI με το SkyCiv.
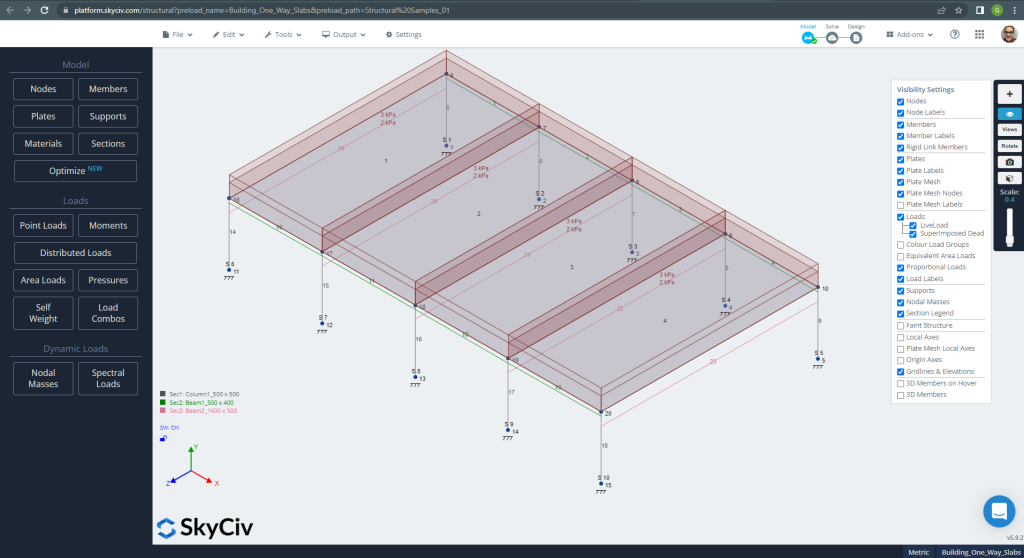
Φιγούρα 10. Δομικό μοντέλο σε S3D παράδειγμα για πλάκες μονής κατεύθυνσης. (Δομικά 3D, SkyCiv Cloud Engineering).
Πριν από την ανάλυση του μοντέλου, πρέπει να ορίσουμε ένα μέγεθος πλέγματος πλάκας. Μερικές αναφορές (2) προτείνετε ένα μέγεθος για το στοιχείο κελύφους του 1/6 του μικρού διαστήματος ή 1/8 του μεγάλου εύρους, το μικρότερο από αυτά. Ακολουθώντας αυτή την τιμή, έχουμε \(\frac{L2}{6}= frac{6Μ}{6} = 1 m \) ή \(\frac{L1}{8}= frac{14Μ}{8}=1,75μ \); παίρνουμε 1 m ως μέγιστο συνιστώμενο μέγεθος και 0,50 m εφαρμοσμένο μέγεθος ματιών.
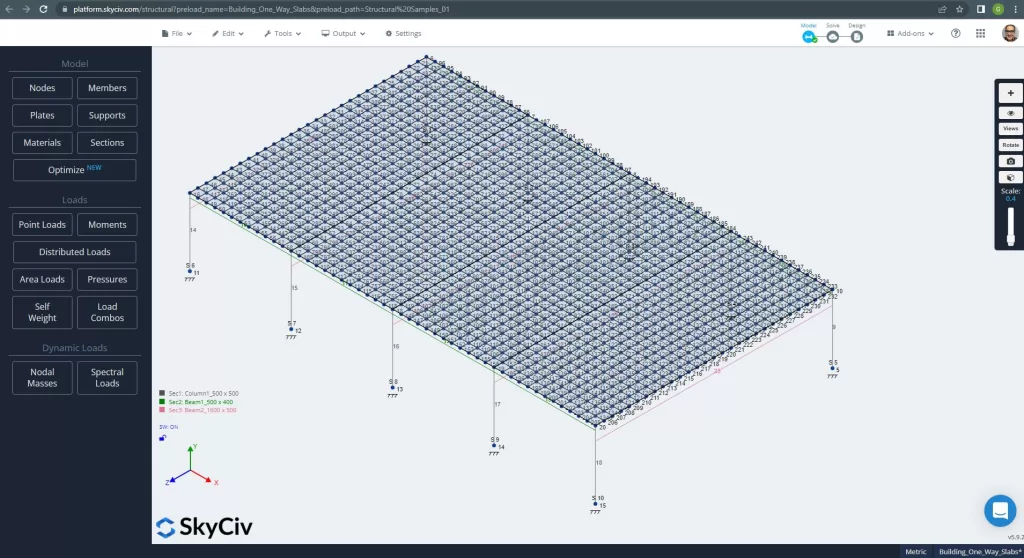
Φιγούρα 11. Βελτιωμένο πλέγμα σε πλάκες. (Δομικά 3D, SkyCiv Cloud Engineering).
Μόλις βελτιώσαμε το αναλυτικό δομικό μας μοντέλο, κάνουμε γραμμική ελαστική ανάλυση. Κατά το σχεδιασμό πλακών, πρέπει να ελέγξουμε αν η κατακόρυφη μετατόπιση είναι μικρότερη από τη μέγιστη επιτρεπόμενη από τον κωδικό. Τα Αυστραλιανά Πρότυπα καθιέρωσαν μια μέγιστη κατακόρυφη μετατόπιση με δυνατότητα εξυπηρέτησης \(\frac{μεγάλο}{250}= frac{6000χιλ}{250}=24,0 mm).
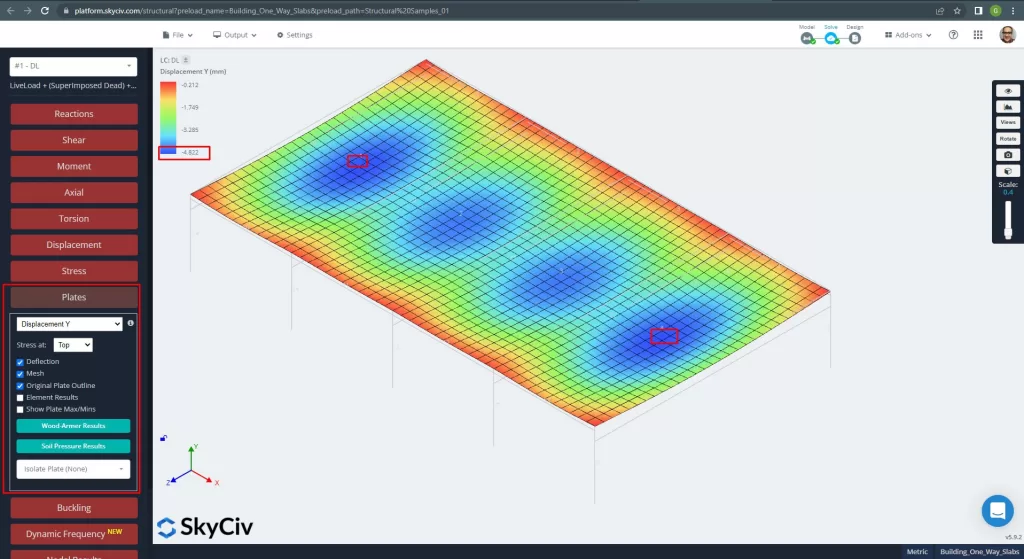
Φιγούρα 12. Κατακόρυφη μετατόπιση σε πλάκες. (Δομικά 3D, SkyCiv Cloud Engineering).
Σύγκριση της μέγιστης κατακόρυφης μετατόπισης με την τιμή που αναφέρεται στον κωδικό, η ακαμψία της πλάκας είναι επαρκής. \(4.822 χιλ < 24.00mm).
Οι μέγιστες ροπές στα ανοίγματα της πλάκας βρίσκονται για θετικές στο κέντρο και για αρνητικές στα εξωτερικά και εσωτερικά στηρίγματα. Ας δούμε τις τιμές αυτών των στιγμών στις παρακάτω εικόνες.
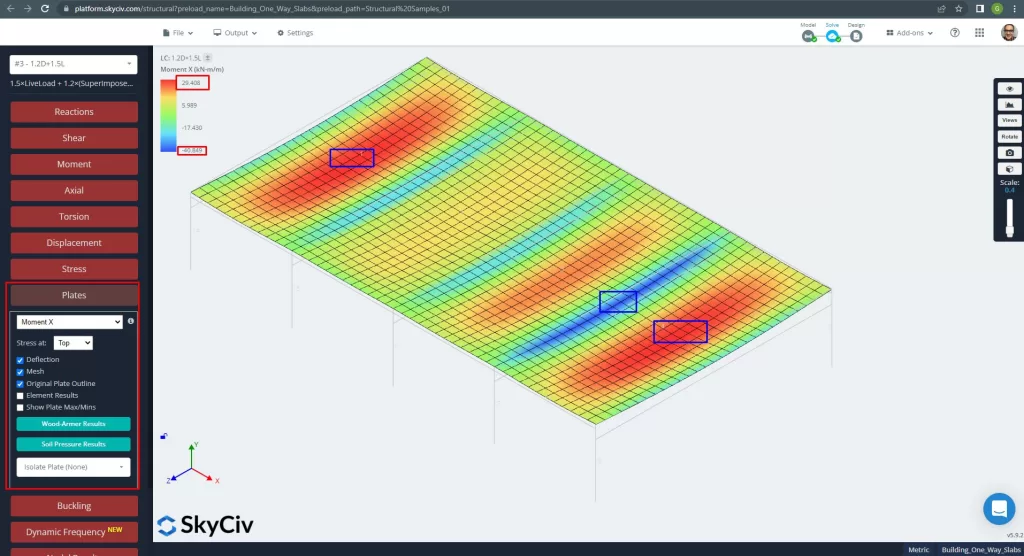
Φιγούρα 13. Στιγμές προς την κατεύθυνση Χ. (Δομικά 3D, SkyCiv Cloud Engineering).
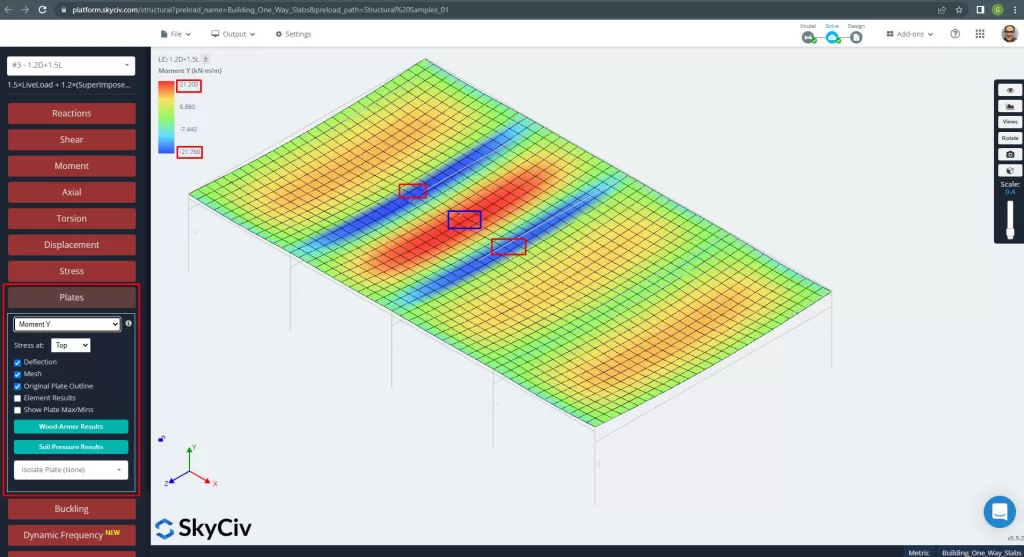
Φιγούρα 14. Στιγμές προς την κατεύθυνση Υ. (Δομικά 3D, SkyCiv Cloud Engineering).
Οι τοπικοί άξονες στοιχείων πλάκας υποδεικνύονται παρακάτω.
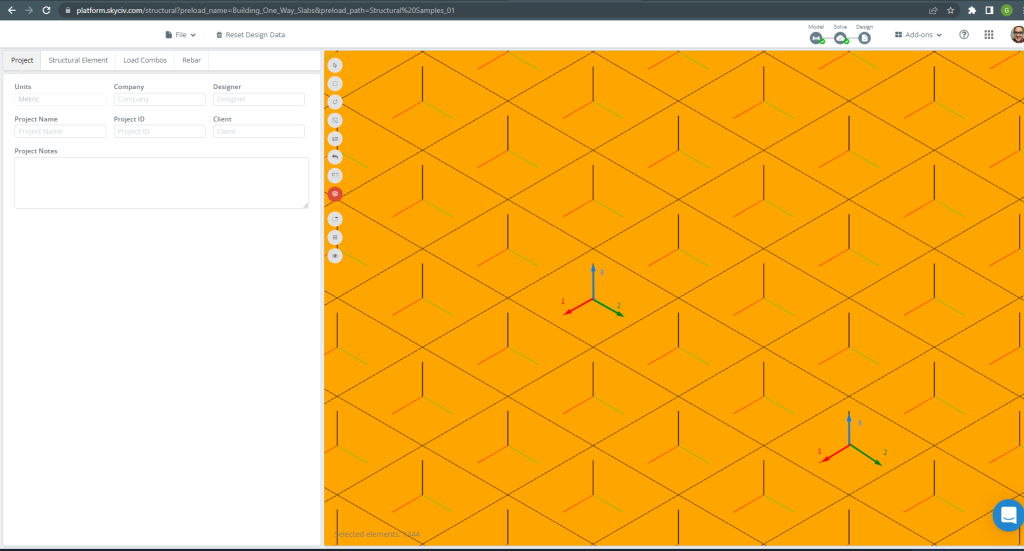
Φιγούρα 15. Τοπικοί άξονες πλακών. (Δομικά 3D, SkyCiv Cloud Engineering).
Για περισσότερες λεπτομέρειες σχετικά με την αυτοματοποιημένη σχεδίαση ενισχυμένων πλακών, δείτε την τεκμηρίωσή μας Πιάτα στο SkyCiv.
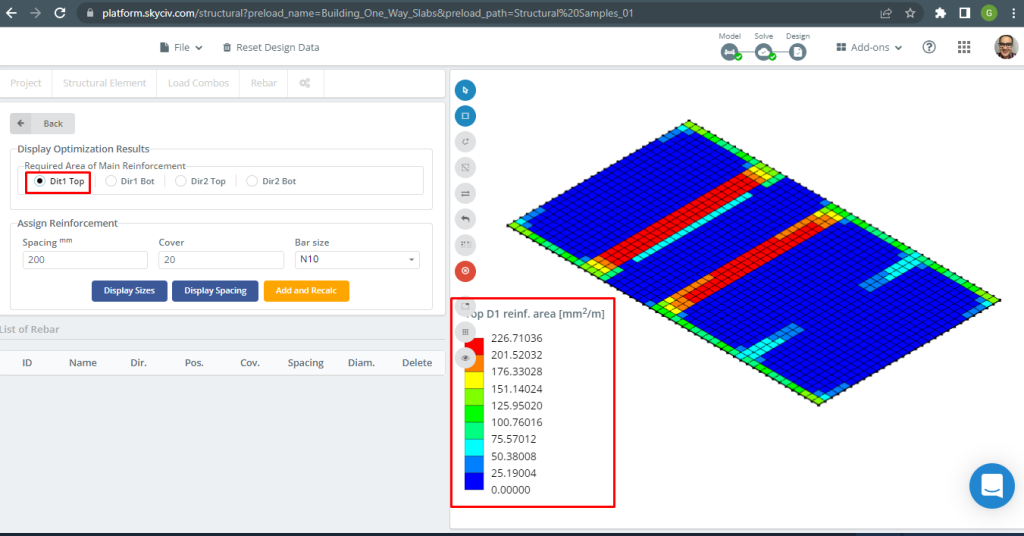
Φιγούρα 16. Κορυφαία ενίσχυση D1. (Δομικά 3D, SkyCiv Cloud Engineering).
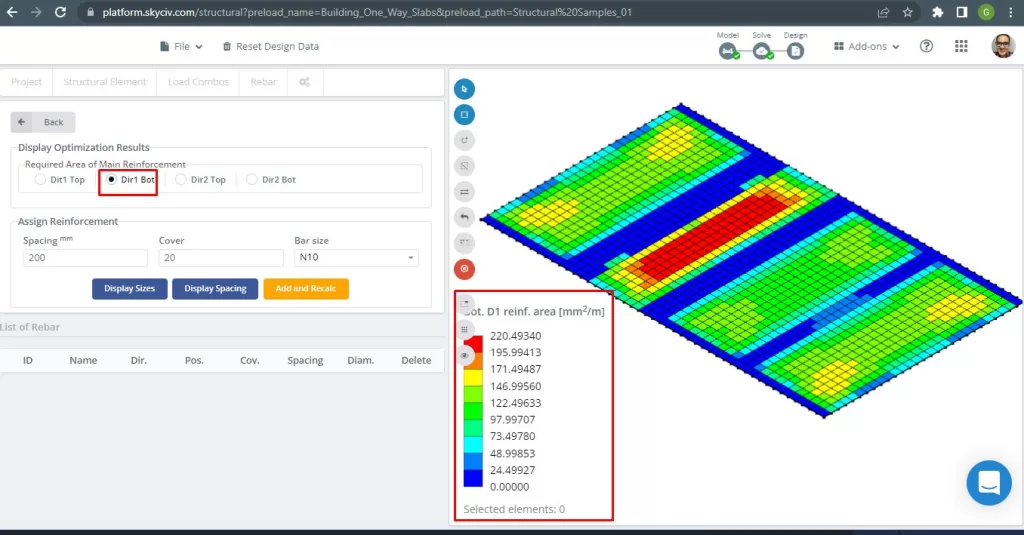
Φιγούρα 17. Κάτω ενίσχυση D1. (Δομικά 3D, SkyCiv Cloud Engineering).
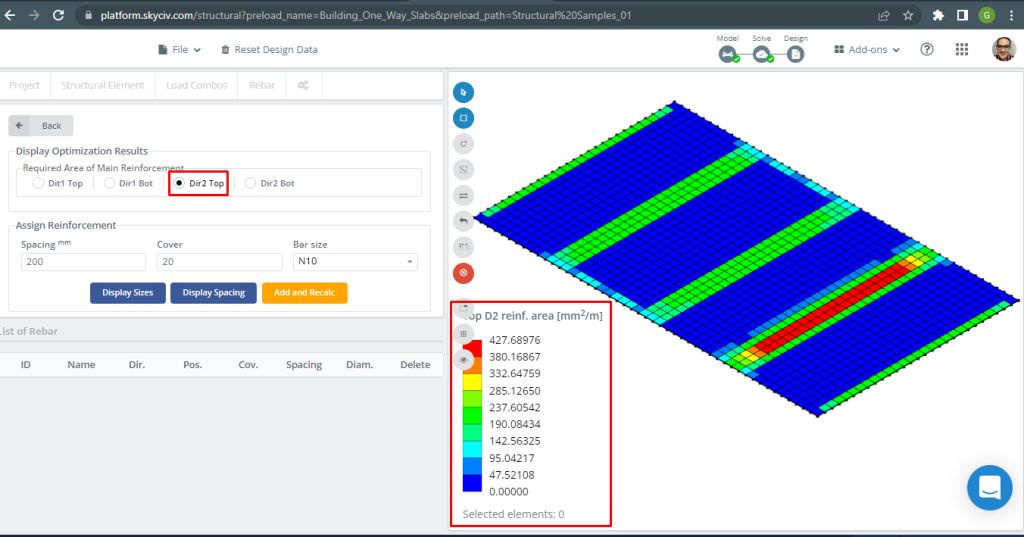
Φιγούρα 18. Κορυφαία ενίσχυση D2. (Δομικά 3D, SkyCiv Cloud Engineering).
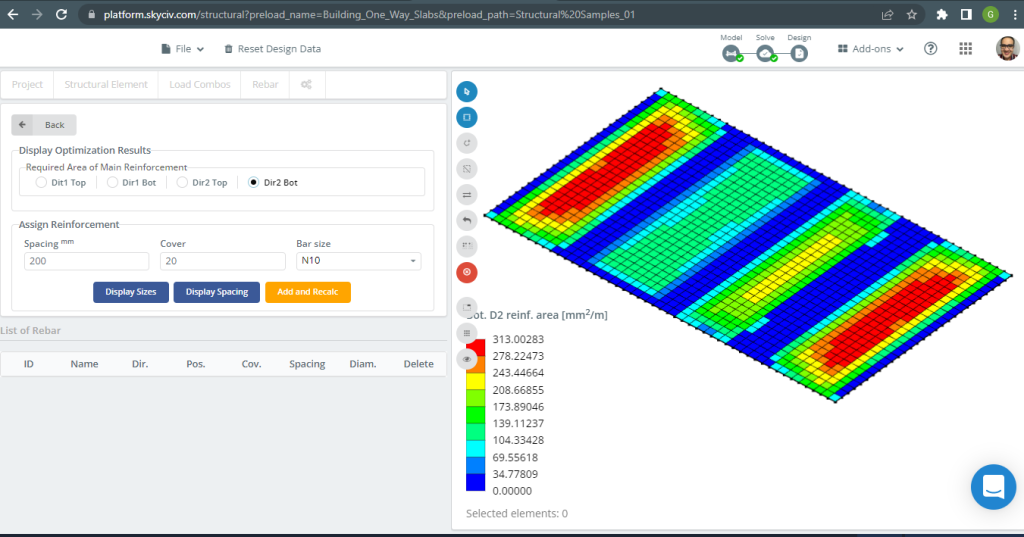
Φιγούρα 19. Κάτω ενίσχυση D2. (Δομικά 3D, SkyCiv Cloud Engineering).
Σύγκριση αποτελεσμάτων
Το τελευταίο βήμα σε αυτό το παράδειγμα σχεδίασης πλάκας μονής κατεύθυνσης είναι η σύγκριση της επιφάνειας του χαλύβδινου οπλισμού που ελήφθη με ανάλυση S3D (τοπικούς άξονες “2”) και υπολογισμοί χειρός.
| Στιγμές και περιοχή χάλυβα | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| \(ΕΝΑ_{αγ, HandCalcs} {mm^2}\) | 334.82 | 436.31 | 481.099 | 481.099 | 334.8214 | 436.3100 |
| \(ΕΝΑ_{αγ, S3D} {mm^2}\) | 285.13 | 313.00 | 427.69 | 427.69 | 313.00 | 427.69 |
| \(\Δέλτα_{διαφ}\) (%) | 14.84 | 28.262 | 11.101 | 11.101 | 6.517 | 1.986 |
Μπορούμε να δούμε ότι τα αποτελέσματα των τιμών είναι πολύ κοντά μεταξύ τους. Αυτό σημαίνει ότι οι υπολογισμοί είναι σωστοί!
Παράδειγμα σχεδίασης πλακών διπλής κατεύθυνσης
Σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ, θα αναπτύξουμε ένα παράδειγμα που αποτελείται από ένα σύστημα grillage.
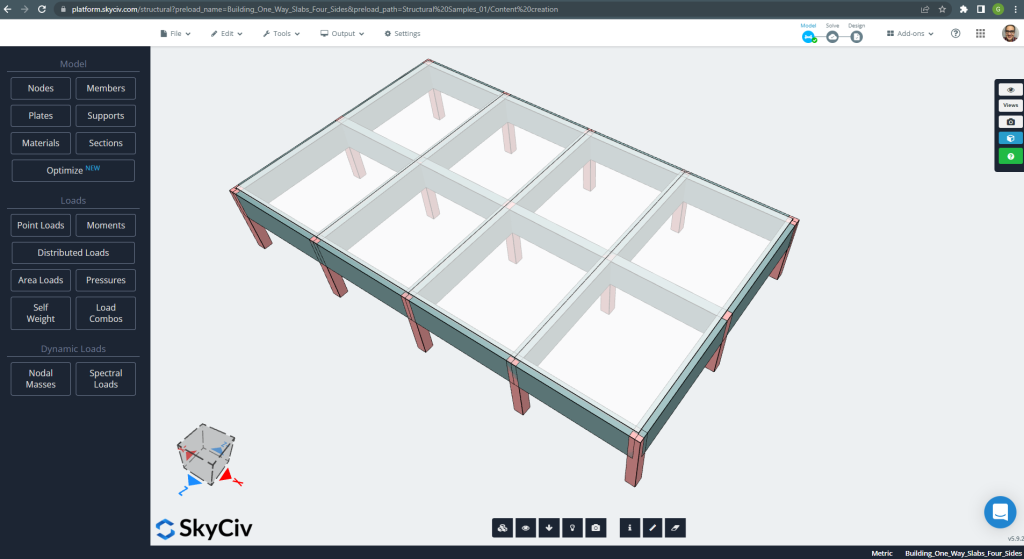
Φιγούρα 20. Σύστημα Grillage. (Δομικά 3D, SkyCiv Cloud Engineering).
Οι διαστάσεις του σχεδίου φαίνονται στη συνέχεια
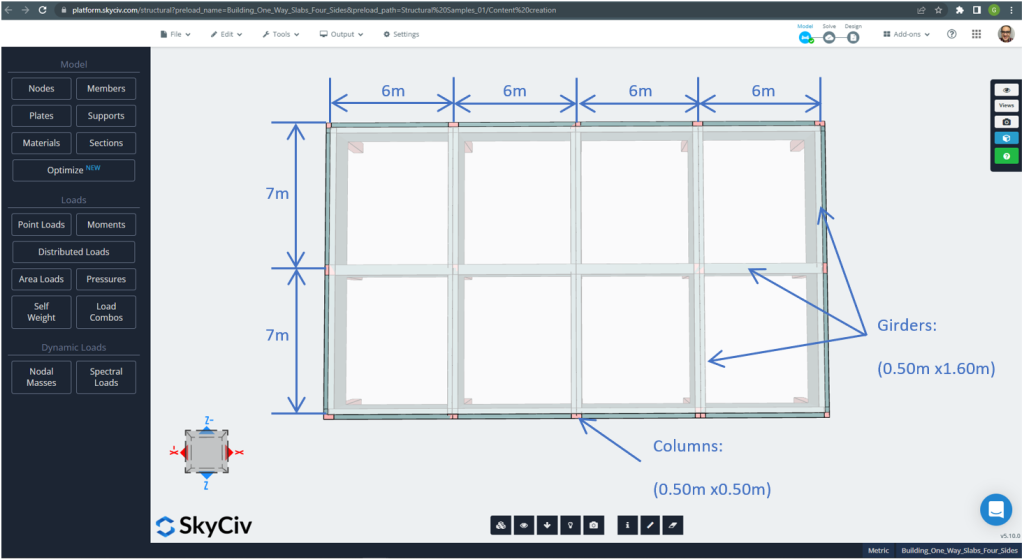
Φιγούρα 21. Σχεδιάστε τις διαστάσεις για τις τέσσερις πλευρές αμφίδρομη πλάκα παράδειγμα. (Δομικά 3D, SkyCiv Cloud Engineering).
Για το παράδειγμα πλάκας, Συνοψίζοντας, το υλικό, ιδιότητες στοιχείων, και φορτία που πρέπει να ληφθούν υπόψη :
- Ταξινόμηση τύπου πλάκας: Δύο – τρόπο συμπεριφοράς \(\frac{L_2}{L_1} \ο 2 ; \frac{7Μ}{6Μ}=1,167 < 2.00 \) Εντάξει!
- Επάγγελμα κτιρίου: Οικιστική χρήση
- Πάχος πλάκας \(αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{πλάκα}=0,25m)
- Πυκνότητα οπλισμένου σκυροδέματος υποθέτοντας αναλογία οπλισμού χάλυβα ίση με 0.5% \(\rho_w = 24 \frac{ΚΝ}{m^3} + 0.6 \frac{ΚΝ}{m^3} \φορές 0.5 = 24.3 \frac{ΚΝ}{m^3} \)
- Χαρακτηριστική θλιπτική αντοχή σκυροδέματος στο 28 μέρες \(f’c = 25 MPa \)
- Concrete Modulus of Elasticity by Australian Standard \(E_c = 26700 MPa \)
- Πλάκα Αυτο-βάρος \(Νεκρό = rho_w φορές t_{πλάκα} = 24.3 \frac{ΚΝ}{m^3} \φορές 0,25m = 6.075 \frac {ΚΝ}{m^2}\)
- Υπερ-επιβεβλημένο νεκρό φορτίο \(SD = 3.0 \frac {ΚΝ}{m^2}\)
- Ζωντανό φορτίο \(L = 2.0 \frac {ΚΝ}{m^2}\)
Υπολογισμός με το χέρι σύμφωνα με το Πρότυπο AS3600
Σε ΑΥΤΗΝ την ΕΝΟΤΗΤΑ, θα υπολογίσουμε την απαιτούμενη ράβδο από ενισχυμένο χάλυβα χρησιμοποιώντας την αναφορά του Αυστραλιανού Προτύπου. Αρχικά λαμβάνουμε τη συνολική συντελεστή ροπής κάμψης που πρέπει να πραγματοποιηθεί από τις ενιαίες λωρίδες πλάτους της πλάκας σε κάθε κύρια διεύθυνση κάμψης.
- Νεκρό φορτίο, \(g = (3.0 + 6.075) \frac{ΚΝ}{m^2} \φορές 1 m = 9.075 \frac{ΚΝ}{Μ}\)
- Ζωντανό φορτίο, \(q = (2.0) \frac{ΚΝ}{m^2} \φορές 1 m = 2.0 \frac{ΚΝ}{Μ}\)
- Απόλυτο φορτίο, \(Fd = 1,2 φορές g + 1.5\φορές q = (1.2\φορές 9.075 + 1.5\φορές 2.0)\frac{ΚΝ}{Μ} =13,89 φράκ{ΚΝ}{Μ} \)
Σχεδιάστε στιγμές και συντελεστές
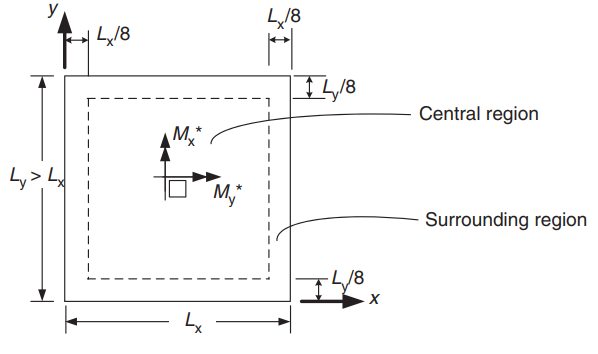
Φιγούρα 22. Προσανατολισμός πλάκας διπλής κατεύθυνσης για καθορισμό θετικών ροπών. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press)
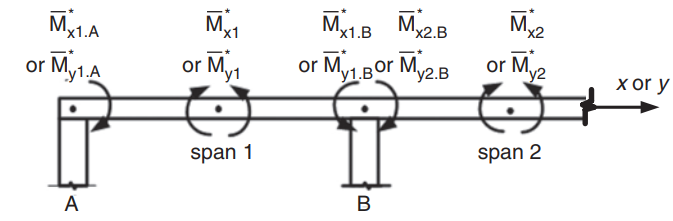
Φιγούρα 23. Προσδιορισμός αρνητικών ροπών σε αμφίδρομη πλάκα. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press)
| Κατάσταση άκρης | Συντελεστές μικρού εύρους (\(\beta_x)) | Συντελεστές μεγάλου εύρους (\(\beta_y)\) όλες οι αξίες του \(\frac{L_y}{L_x}\) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Τιμές του \(\frac{L_y}{L_x}\) | |||||||||
| 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.75 | \(\cdot K_a 2.0\) | ||
| 1. Τέσσερις άκρες συνεχόμενες | 0.024 | 0.028 | 0.032 | 0.035 | 0.037 | 0.040 | 0.044 | 0.048 | 0.024 |
| 2. Ένα κοντό άκρο διακοπεί | 0.028 | 0.032 | 0.036 | 0.038 | 0.041 | 0.043 | 0.047 | 0.050 | 0.028 |
| 3. Ένα μακρύ άκρο ασυνεχές | 0.028 | 0.035 | 0.041 | 0.046 | 0.050 | 0.054 | 0.061 | 0.066 | 0.028 |
| 4. Δύο κοντές άκρες ασυνεχείς | 0.034 | 0.038 | 0.040 | 0.043 | 0.045 | 0.047 | 0.050 | 0.053 | 0.034 |
| 5. Δύο μακριές άκρες ασυνεχείς | 0.034 | 0.046 | 0.056 | 0.065 | 0.072 | 0.078 | 0.091 | 0.100 | 0.034 |
| 6. Δύο γειτονικές ακμές ασυνεχείς | 0.035 | 0.041 | 0.046 | 0.051 | 0.055 | 0.058 | 0.065 | 0.070 | 0.035 |
| 7. Τρεις άκρες ασυνεχείς (μια μακρά άκρη συνεχόμενη) | 0.043 | 0.049 | 0.053 | 0.057 | 0.061 | 0.064 | 0.069 | 0.074 | 0.043 |
| 8. Τρεις άκρες ασυνεχείς (ένα κοντό άκρο συνεχές) | 0.043 | 0.054 | 0.064 | 0.072 | 0.078 | 0.084 | 0.096 | 0.105 | 0.043 |
| 9. Τέσσερις άκρες ασυνεχείς | 0.056 | 0.066 | 0.074 | 0.081 | 0.087 | 0.093 | 0.103 | 0.111 | 0.056 |
Τραπέζι 1. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press)
Η παρακάτω εικόνα εξηγεί και τις εννέα περιπτώσεις στις οποίες αναφέρεται ο παραπάνω πίνακας
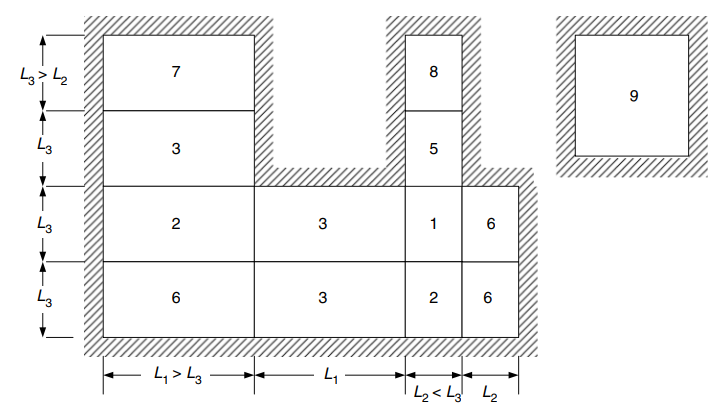
Φιγούρα 24. Συνθήκες ακμών για πλάκες διπλής κατεύθυνσης που στηρίζονται σε τέσσερις πλευρές. (Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press)
Σχεδιαστικές στιγμές για την κεντρική περιοχή (Υπόθεση 6 Δύο γειτονικές ακμές ασυνεχείς) :
- \(L_x = 6m, L_y=7m, \frac{L_y}{L_x} = frac{7Μ}{6Μ}= 1.167 \) Οι τιμές πρέπει να παρεμβάλλονται γραμμικά
- Θετικά:
- \(M_x = {\beta_x}{F_d}{L_x^2} = {0.04435}\φορές {13.89 \frac{ΚΝ}{Μ}}\φορές{(6Μ)^ 2}=22,177 kNm)
- \(M_y = {\beta_y}{F_d}{L_x^2} ={0.035}\φορές {13.89 \frac{ΚΝ}{Μ}}\φορές{(6Μ)^ 2}=17.501 kNm \)
- Αρνητικά Εξωτερικό άνοιγμα:
- \(Μ_{x1, Α} = -\lambda_e \times M_x = -0.5 \φορές 22.177 kNm = – 11.089 kNm\)
- \(Μ_{y1, Α} = -\lambda_e \times M_y = -0.5 \φορές 17.501 kNm = -8.751 kNm \)
- Αρνητικά Εσωτερικό άνοιγμα:
- \(Μ_{x1, Β} = -\lambda_{1Χ} \φορές M_x = -1.33 \φορές 22.177 kNm = – 29.495 kNm\)
- \(Μ_{y1, σι} = -\lambda_{1και} \φορές M_y = -1.33 \φορές 17.501 kNm = -23.276 kNm \)
Σχεδιαστικές στιγμές για την κεντρική περιοχή (Υπόθεση 3 Ένα μακρύ άκρο ασυνεχές) :
- \(L_x = 6m, L_y=7m, \frac{L_y}{L_x} = frac{7Μ}{6Μ}= 1.167 \) Οι τιμές πρέπει να παρεμβάλλονται γραμμικά
- Θετικά:
- \(M_x = {\beta_x}{F_d}{L_x^2} = {0.03902}\φορές {13.89 \frac{ΚΝ}{Μ}}\φορές{(6Μ)^ 2}= 19.512 kNm\)
- \(M_y = {\beta_y}{F_d}{L_x^2} ={0.028}\φορές {13.89 \frac{ΚΝ}{Μ}}\φορές{(6Μ)^ 2}= 14.001 kNm \)
- Αρνητικά Εσωτερικό άνοιγμα:
- \(Μ_{x1, Β} = -\lambda_{1Χ} \φορές M_x = -1.33 \φορές 19.512 kNm = – 25.951 kNm\)
- \(Μ_{y1, Β} = -\lambda_{1και} \φορές M_y = -1.33 \φορές 14.001 kNm = – 18.621 kNm \)
- Αρνητικά εσωτερικό δεύτερο άνοιγμα:
- \(Μ_{x2,B} = -\lambda_{2Χ} \φορές M_x = -1.33 \φορές 19.512 kNm = – 25.951 kNm\)
- \(Μ_{y2,B} = -\lambda_{2και} \φορές M_y = -1.33 \φορές 14.001 kNm = – 18.621 kNm \)
Χάλυβας οπλισμού για Χ κατεύθυνση
| \(\alpha\) και Στιγμές | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| Τιμή M | 11.089 | 22.177 | 29.495 | 25.951 | 19.512 | 25.951 |
| \(\rho_t\) | 0.00055614 | 0.00112 | 0.001496 | 0.001313 | 0.000984 | 0.001313 |
| προς την | 0.015395 | 0.0310 | 0.0414 | 0.0364 | 0.0272 | 0.0364 |
| \(\φι) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(ΕΝΑ_{αγ} {mm^2}\) | 334.8214 | 334.8214 | 335.08233 | 334.821 | 334.8214 | 334.8214 |
Χάλυβας οπλισμού για κατεύθυνση Υ
| \(\alpha\) και Στιγμές | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| Τιμή M | 8.751 | 17.501 | 23.276 | 18.621 | 14.001 | 18.621 |
| \(\rho_t\) | 0.0004383 | 0.0008811 | 0.001176 | 0.0009381 | 0.000703 | 0.0009381 |
| προς την | 0.0121 | 0.0244 | 0.03256 | 0.02597 | 0.0195 | 0.02597 |
| \(\φι) | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 | 0.8 |
| \(ΕΝΑ_{αγ} {mm^2}\) | 334.821 | 334.821 | 334.821 | 334.821 | 334.8214 | 334.821 |
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
Αποτελέσματα ενότητας σχεδίασης πλακών SkyCiv S3D
Μετά τη βελτίωση του μοντέλου, είναι καιρός να εκτελέσουμε μια γραμμική ελαστική ανάλυση.
Κατά το σχεδιασμό πλακών, πρέπει να ελέγξουμε αν η κατακόρυφη μετατόπιση είναι μικρότερη από τη μέγιστη επιτρεπόμενη από τον κωδικό. Τα Αυστραλιανά Πρότυπα καθιέρωσαν μια μέγιστη κατακόρυφη μετατόπιση με δυνατότητα εξυπηρέτησης \(\frac{μεγάλο}{250}= frac{6000χιλ}{250}=24,0 mm).
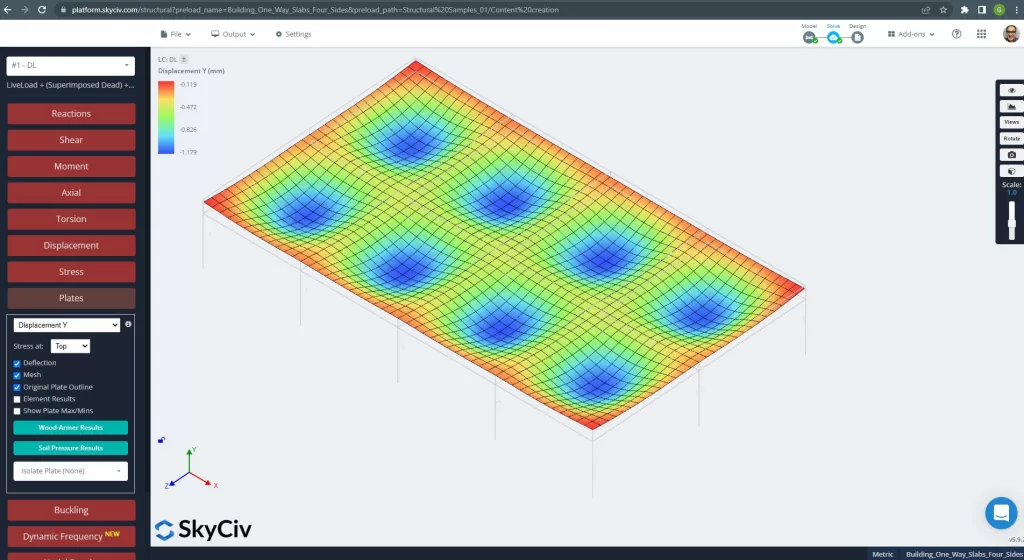
Φιγούρα 25. Κατακόρυφη Μετατόπιση στο σύστημα πλακών grillage. (Δομικά 3D, SkyCiv Cloud Engineering).
Η παραπάνω εικόνα μας δίνει την κατακόρυφη μετατόπιση. Η μέγιστη τιμή είναι -1,179mm όντας μικρότερη από τη μέγιστη επιτρεπόμενη των -24mm. Επομένως, η ακαμψία της πλάκας είναι επαρκής.
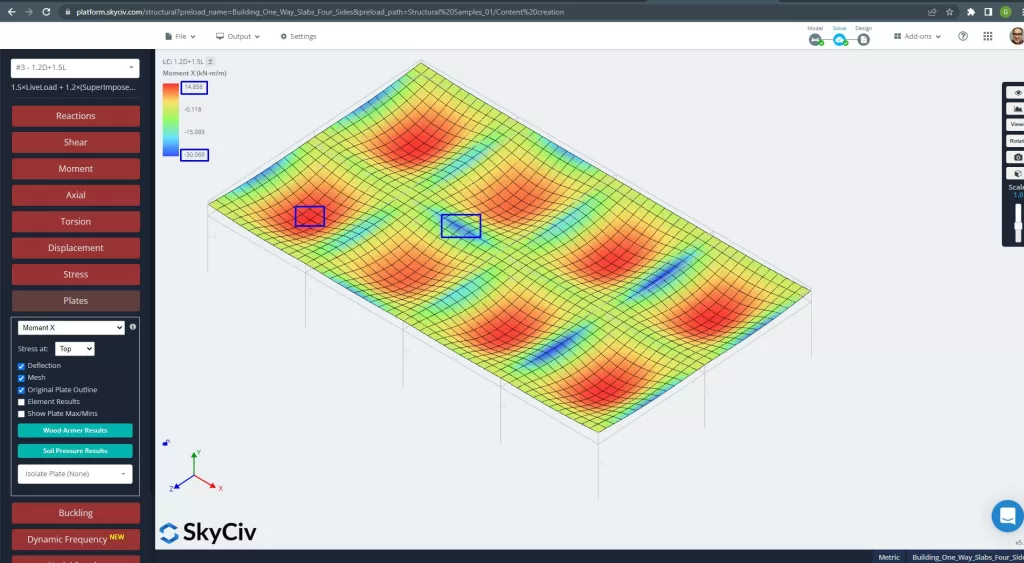
Φιγούρα 26. Πλάκες στιγμές προς την κατεύθυνση Χ. (Δομικά 3D, SkyCiv Cloud Engineering).
εικόνες 27 και 28 αποτελούνται από τη ροπή κάμψης σε κάθε κύρια κατεύθυνση. Λαμβάνοντας την κατανομή της στιγμής και τις τιμές, το λογισμικό, SkyCiv, μπορεί να αποκτήσει τότε τη συνολική επιφάνεια οπλισμού χάλυβα.
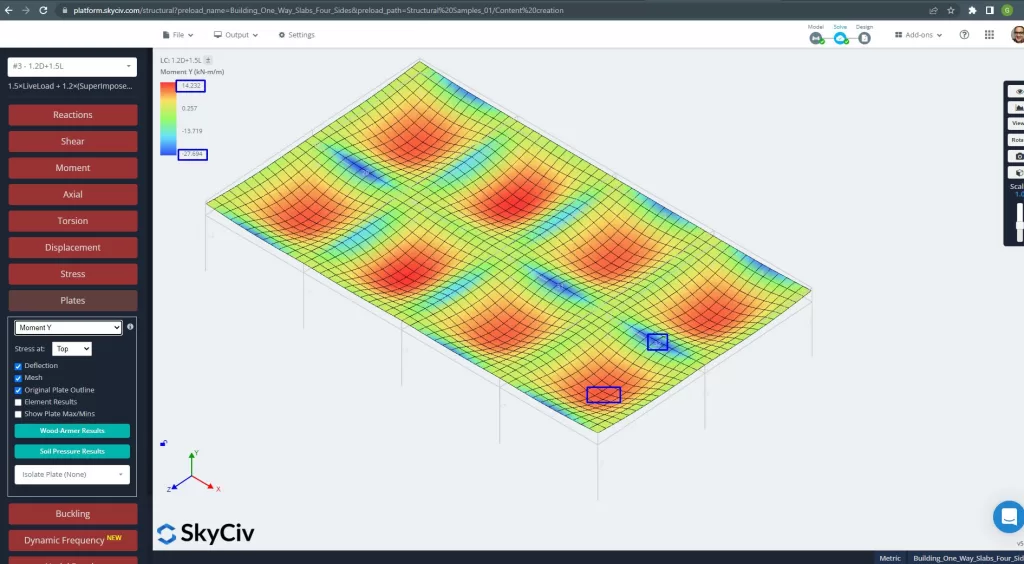
Φιγούρα 27. Πλάκες στιγμές προς την κατεύθυνση Υ. (Δομικά 3D, SkyCiv Cloud Engineering).
Χώροι ενίσχυσης από χάλυβα:
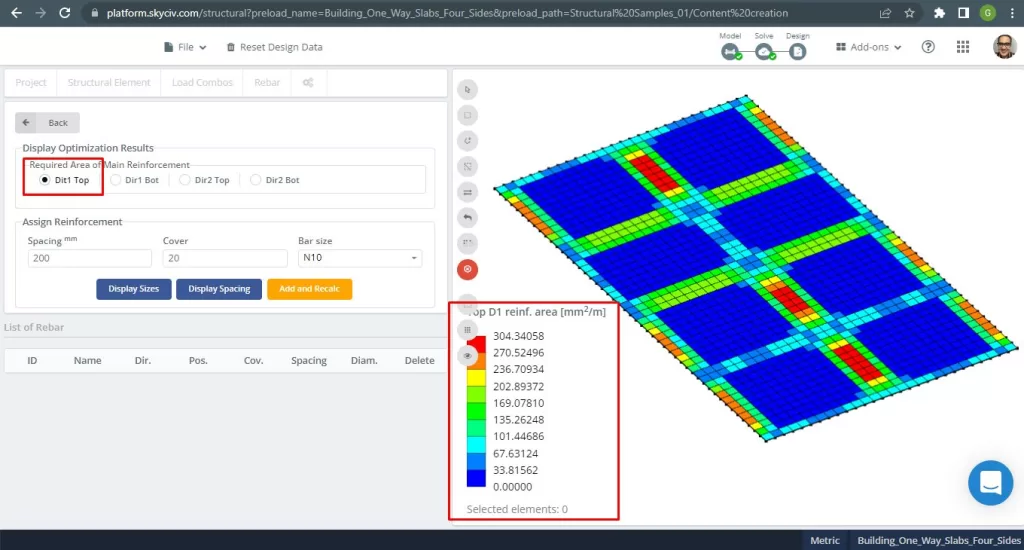
Φιγούρα 28. Κορυφαίος οπλισμός οπλισμού από χάλυβα κατ' κατεύθυνση 1. (Δομικά 3D, SkyCiv Cloud Engineering).
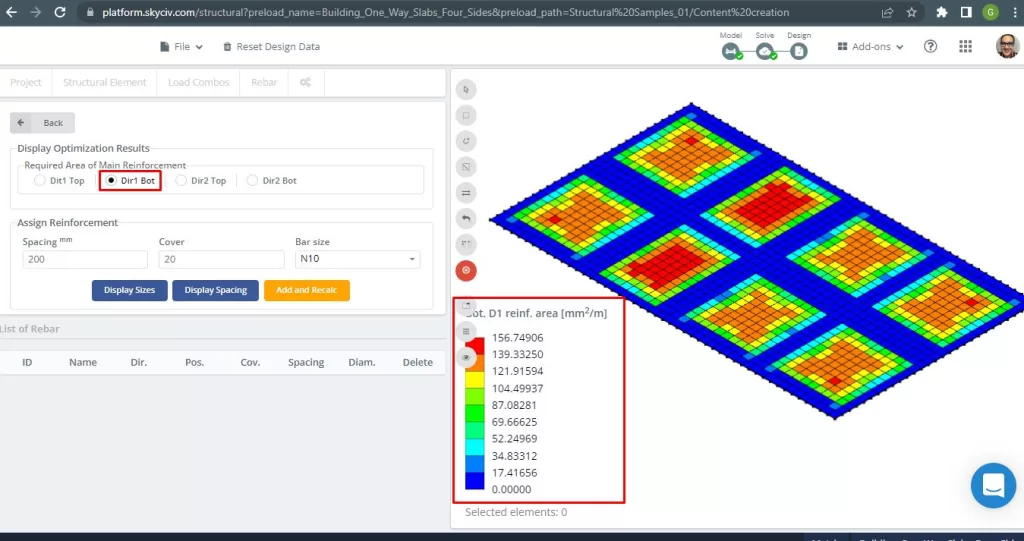
Φιγούρα 29. Ενίσχυση οπλισμού κάτω από χάλυβα κατ' κατεύθυνση 1. (Δομικά 3D, SkyCiv Cloud Engineering).
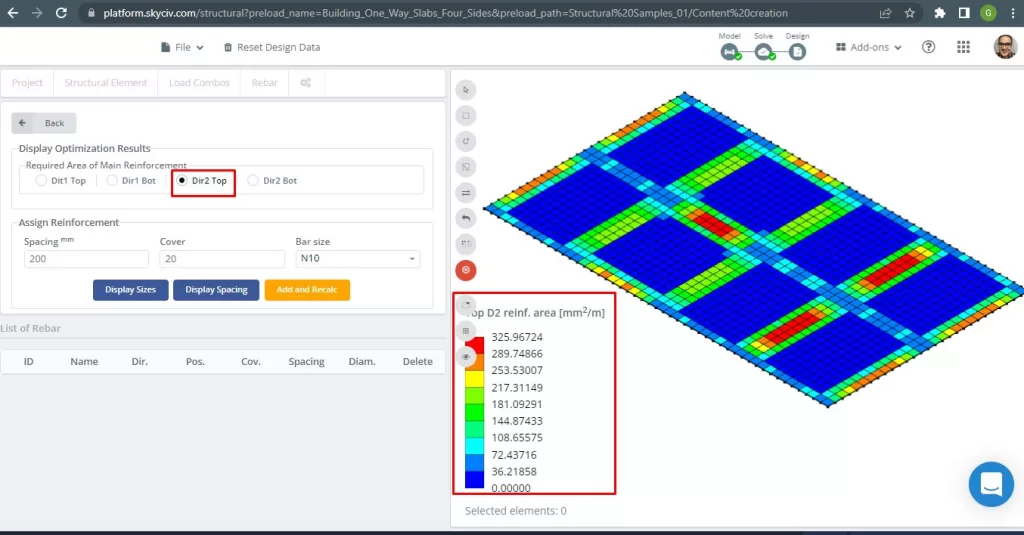
Φιγούρα 30. Κορυφαίος οπλισμός οπλισμού από χάλυβα κατ' κατεύθυνση 2. (Δομικά 3D, SkyCiv Cloud Engineering).
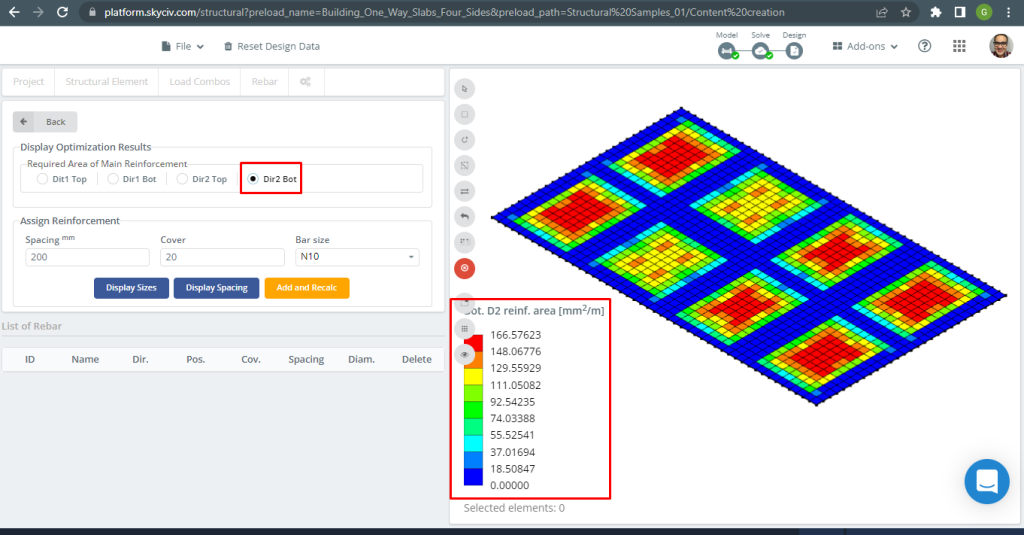
Φιγούρα 31. Ενίσχυση οπλισμού κάτω από χάλυβα κατ' κατεύθυνση 2. (Δομικά 3D, SkyCiv Cloud Engineering).
Σύγκριση αποτελεσμάτων
Το τελευταίο βήμα σε αυτό το παράδειγμα σχεδίασης πλάκας μονής κατεύθυνσης είναι η σύγκριση της επιφάνειας της χαλύβδινης ράβδου που λαμβάνεται με ανάλυση S3D και υπολογισμούς με το χέρι.
Χάλυβας οπλισμού για Χ κατεύθυνση
| Στιγμές και περιοχή χάλυβα | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| \(ΕΝΑ_{αγ, HandCalcs} {mm^2}\) | 334.8214 | 334.8214 | 335.08233 | 334.821 | 334.8214 | 334.8214 |
| \(ΕΝΑ_{αγ, S3D} {mm^2}\) | 289.75 | 149.35 | 325.967 | 325.967 | 116.16 | 217.311 |
| \(\Δέλτα_{διαφ}\) (%) | 13.461 | 55.39 | 2.720 | 2.644 | 65.307 | 35.0964 |
Χάλυβας οπλισμού για κατεύθυνση Υ
| Στιγμές και περιοχή χάλυβα | Εξωτερικό Αρνητικό Αριστερά | Εξωτερικό Θετικό | Εξωτερικό Αρνητικό Δεξιά | Εσωτερικό Αρνητικό Αριστερά | Εσωτερικό θετικό | Εσωτερικό Αρνητικό Δεξί |
|---|---|---|---|---|---|---|
| \(ΕΝΑ_{αγ, HandCalcs} {mm^2}\) | 334.821 | 334.821 | 334.821 | 334.821 | 334.821 | 334.821 |
| \(ΕΝΑ_{αγ, S3D} {mm^2}\) | 270.524 | 156.75 | 304.34 | 304.34 | 156.75 | 270.52 |
| \(\Δέλτα_{διαφ}\) (%) | 19.203 | 53.184 | 9.104 | 9.104 | 53.184 | 19.204 |
Η διαφορά είναι αρκετά υψηλή για θετικές ροπές και ο λόγος θα ήταν η παρουσία δοκών με υψηλή στρεπτική ακαμψία που επηρεάζουν τα αποτελέσματα της ανάλυσης πεπερασμένων στοιχείων πλακών και τους υπολογισμούς για την κάμψη του χάλυβα οπλισμού.
Εάν είστε νέος στο SkyCiv, Εγγραφείτε και δοκιμάστε μόνοι σας το λογισμικό!
βιβλιογραφικές αναφορές
- Yew-Chaye Loo & Sanual Hug Chowdhury , “Οπλισμένο και Προεντεταμένο Σκυρόδεμα”, 2η έκδοση, Cambridge University Press.
- Μπαζάν Ενρίκε & Μελί Πιράλλα, “Σεισμική Μελέτη Κατασκευών”, 1εκδ, ΣΑΦΗ.
- η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από, Κατασκευές από σκυρόδεμα, ΟΠΩΣ ΚΑΙ 3600:2018


