Ροή εργασιών σχεδίασης Spread Footing

Οι βάσεις είναι δομικά μέλη που χρησιμοποιούνται για τη στήριξη υποστυλωμάτων και άλλων κατακόρυφων στοιχείων για τη μετάδοση των φορτίων υπερκατασκευής τους στα υποκείμενα εδάφη.

Φιγούρα 1 απεικονίζει τη διαδικασία ροής εργασιών σχεδιασμού, ΔΙΑΔΙΚΑΣΙΑ ΡΟΗΣ ΕΡΓΑΣΙΑΣ ΣΧΕΔΙΑΣΜΟΥ Στο Σχήμα Ίδρυμα SkyCiv προσαρμόζει τη διαδικασία ροής εργασίας. Όπου αυτοί οι έλεγχοι όπως π.χ (1) Έδαφος, (2) Κουρεύω, (3) Κάμψη, (4) Διπλή διάτμηση, (5) Ανύψωση, και (6) Οι έλεγχοι σταθερότητας είναι σημαντικές παράμετροι που απαιτούνται για την ικανοποίηση του αποτελέσματος χωρίς υπέρβαση της επιτρεπόμενης αναλογίας χρησιμότητας.

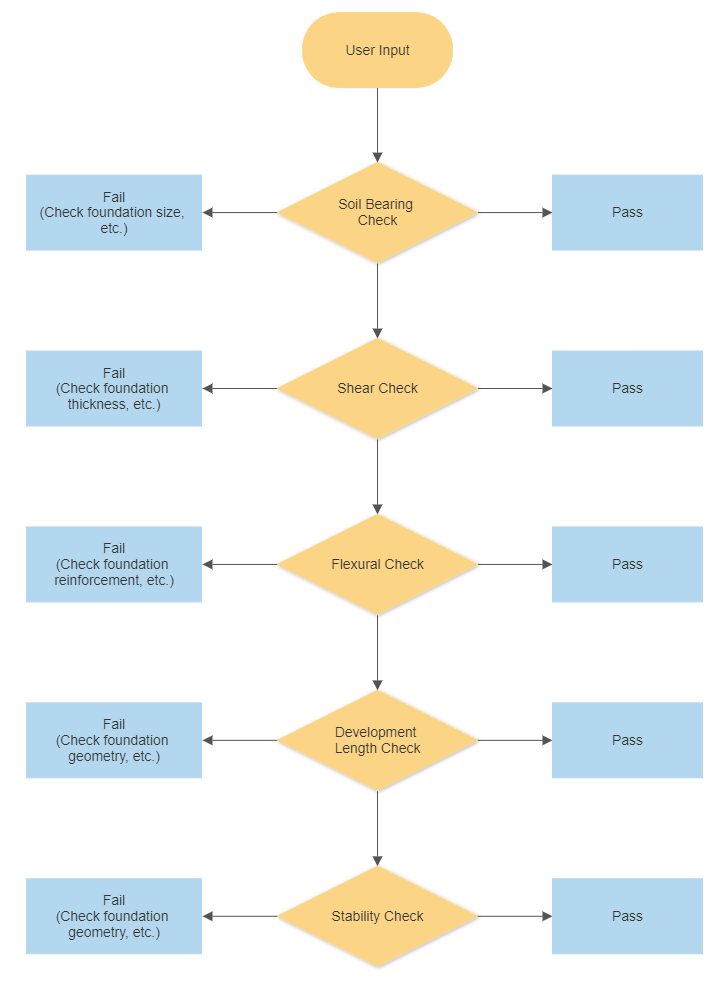
Φιγούρα 1: Ροή εργασιών του Ίδρυμα SkyCiv.

Πώς να σχεδιάσετε το Spread Footing

Αυτή η ενότητα εξετάζει τη διαδικασία σχεδιασμού της βάσης απλώματος σε σχέση με το American Concrete Institute 318-2014.

Οι έλεγχοι μήκους ανάπτυξης και σταθερότητας είναι σημαντικές παράμετροι που απαιτούνται για να ικανοποιηθεί το αποτέλεσμα χωρίς να υπερβαίνει την τιμή του

Ο Έλεγχος Έδρασης Εδάφους καθορίζει κυρίως τις γεωμετρικές διαστάσεις μιας απομονωμένης βάσης από την υπερκατασκευή (υπηρεσία ή απαραίτητες) φορτία. Η πραγματική φέρουσα πίεση προσδιορίζεται κυρίως από την παρακάτω εξίσωση:

\( q_{ένα} = frac{ Π}{ΕΝΑ } \pm frac{ Μ_{Χ} }{ ΜΙΚΡΟ_{Χ} } \pm frac{ Μ_{και} }{ ΜΙΚΡΟ_{και} }\)Ωστόσο, η παραπάνω εξίσωση ισχύει μόνο εάν οι εκκεντρότητες είναι εντός του πυρήνα ( \( \frac{μεγάλο}{6} \) ) του θεμελίου όπου υπάρχει φέρουσα πίεση σε όλη την περιοχή.

Όταν οι εκκεντρότητες ξεπέρασαν τον πυρήνα, εξηγείται το λεπτομερές άρθρο σχετικά με το σχέδιο πίεσης ρουλεμάν εδώ.

Για να ικανοποιηθούν οι γεωμετρικές διαστάσεις του θεμελίου, η επιτρεπόμενη φέρουσα ικανότητα του εδάφους πρέπει να είναι μεγαλύτερη από τη βασική πίεση κάτω από το πέλμα.

\( \κείμενο{Επιτρεπόμενη φέρουσα ικανότητα} > \κείμενο{ Πραγματικός (Διακυβέρνηση) Δέχεται πίεση στο θεμέλιο} \)

Σημείωση: Καμία τάση στην φέρουσα πίεση στο σχέδιο θεμελίωσης.

 

Έλεγχος διάτμησης

Ο έλεγχος διάτμησης καθορίζει το πάχος ή το βάθος της θεμελίωσης με βάση το διατμητικό φορτίο που προκαλείται από τα φορτία υπερκατασκευής. Υπάρχουν δύο πρωτεύοντες έλεγχοι διάτμησης, ως εξής:

1. Μονόδρομος (ή Δοκός) Κουρεύω
2. Αμφίδρομη (ή Γροθιά) Κουρεύω

Μονόδρομος (ή Δοκός) Κουρεύω

Το κρίσιμο τμήμα για μονόδρομη διάτμηση εκτείνεται σε όλο το πλάτος του πέλματος και βρίσκεται σε απόσταση d από την όψη μιας στήλης.

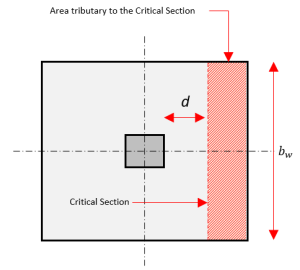
Φιγούρα 2: Μονόδρομη κουρά

Αυτοκρατορικός (psi)

\( V_{ντο} = 2 \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{β} ρε \)

Μετρικός (MPa)

\( V_{ντο} = 0.17 \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{β} ρε \)

Για να ικανοποιήσει το One Way (ή Δοκός) Κουρεύω, ο \( V_{ντο} \) δεν πρέπει να είναι μεγαλύτερη από \( V_{εσύ} \).

\( \phi V_{ντο} > V_{εσύ} = κείμενο{ Πραγματικός (Διακυβέρνηση) Διάτμηση του Ιδρύματος} \)

Διπλής κατεύθυνσης (ή Γροθιά) Κουρεύω

Το κρίσιμο τμήμα για σχεδιασμό αμφίδρομης διάτμησης βρίσκεται στο \( \frac{ρε}{2} \) μακριά από μια τσιμεντένια όψη στήλης. Οπου \( V_{ντο} \) η εξίσωση ορίζεται ως εξής:

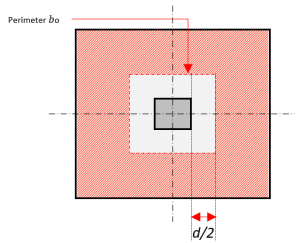
Φιγούρα 3: Αμφίδρομη κουρά

Αυτοκρατορικός (psi)

\( V_{ντο} = αριστερά( 2 + \frac{4}{\βήτα} \σωστά) \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} ρε \)

\( V_{ντο} = αριστερά( \frac{\άλφα_{μικρό} ρε }{ αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} } + 2 \σωστά) \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} ρε \)

\( V_{ντο} = 4 \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} ρε \)

Μετρικός (MPa)

\( V_{ντο} = 0.17 \αριστερά( 1 + \frac{2}{\βήτα} \σωστά) \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} ρε \)

\( V_{ντο} = 0.083 \αριστερά( \frac{ \άλφα_{μικρό} ρε }{ αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} } + 2 \σωστά) \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} ρε \)

\( V_{ντο} = 0.33 \λάμδα sqrt{ σ ^{«}_{ντο} } αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{ο} ρε \)

Η διακυβέρνηση \( V_{ντο} \) θα ληφθεί ως η ελάχιστη τιμή.

Για να ικανοποιήσει το Two Way (ή Γροθιά) Κουρεύω, ο \( V_{ντο} \) δεν πρέπει να είναι μεγαλύτερη από \( V_{εσύ} \).

\( \phi V_{ντο} > V_{εσύ} = κείμενο{ Πραγματικός (Διακυβέρνηση) Διάτμηση του Ιδρύματος} \)

Έλεγχος κάμψης

Ο έλεγχος κάμψης καθορίζει τον απαιτούμενο οπλισμό της θεμελίωσης με βάση τη ροπή ή το φορτίο κάμψης που προκαλείται από τα φορτία της υπερκατασκευής. Η διαδικασία σχεδιασμού για την αντοχή ροπής εξετάζει ένα μονόδρομο καμπτικό μέλος πρώτα σε μία κύρια κατεύθυνση.

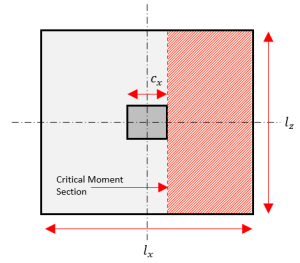
Φιγούρα 4: Γραμμή τομής κρίσιμης στιγμής

Βήμα 1. Υπολογίστε την Πραγματική Ροπή στο θεμέλιο \( Μ_{εσύ} \).

\( Μ_{εσύ} = q_{εσύ} \αριστερά( \frac{ μεγάλο_{Χ} – ντο }{ 2 } \σωστά) μεγάλο_{με} \frac{ μεγάλο_{Χ} – ντο }{ 2 } \)

Βήμα 2. Υπολογίστε τον ελάχιστο απαιτούμενο οπλισμό της θεμελίωσης

Βήμα 3. Υπολογίστηκε το Βάθος του ισοδύναμου ορθογώνιου μπλοκ τάσης, ένα.

\( a = frac{ ΕΝΑ_{μικρό} φά_{και} }{ 0.85 φά_{ντο}^{«} μεγάλο_{με} } \)

Βήμα 4. Υπολογίστε τη Ροπτική Χωρητικότητα της θεμελίωσης \( \ταινία_{ν} \).

\( \ταινία_{ν} = phi Α_{μικρό} φά_{και}\αριστερά( ρε – \frac{ένα}{2} \σωστά) \)

Για να ικανοποιηθεί η απαίτηση κάμψης, ο \( \ταινία_{ν} \) δεν πρέπει να είναι μεγαλύτερη από \( Μ_{εσύ} \)..

\( \ταινία_{ν} > Μ_{εσύ} \)

Έλεγχος μήκους ανάπτυξης

Ο Έλεγχος Μήκους Ανάπτυξης καθορίζει το μικρότερο μήκος ενσωμάτωσης που απαιτείται για μια ράβδο οπλισμού για να αναπτύξει την πλήρη αντοχή της σε διαρροή στο σκυρόδεμα.

 

Έλεγχος σταθερότητας

Υπάρχουν δύο κύριοι τύποι Ελέγχων Σταθερότητας στο θεμέλιο, ως εξής:

1. Ανατροπή
2. Ολίσθηση

Έλεγχος ανατροπής

Ο έλεγχος ανατροπής είναι ένας έλεγχος ευστάθειας έναντι της Ροπής του φορτίου της υπερκατασκευής. Γενικά, αυτός ο συντελεστής ασφάλειας για τη στιγμή της ανατροπής είναι 1.5-3.0.

 

\( \κείμενο{Ανατροπή Συντελεστής Ασφάλειας} < \frac{ \άθροισμα M_{Ρ} }{ \άθροισμα M_{ΟΤ} } \)

Σημείωση:

• \( \άθροισμα M_{Ρ} \) – Αντιστασιακή στιγμή
• \( \άθροισμα M_{ΟΤ} \) – Ανατροπή Στιγμής

 

Συρόμενος έλεγχος

Ο έλεγχος ολίσθησης είναι ένας έλεγχος ευστάθειας έναντι της Οριζόντιας Δύναμης που προκαλείται από το φορτίο της υπερκατασκευής. Γενικά, αυτός ο συντελεστής ασφάλειας για τη στιγμή της ανατροπής είναι 1.5-3.0.

\( \κείμενο{Sliding Factor of Safety} < \κείμενο{Δύναμη ολίσθησης} \)

 

Έλεγχος ανύψωσης

Ελέγχει το ρυθμιζόμενο αξονικό φορτίο που επενεργεί στο πέλμα. Αθροίζει όλα τα κατακόρυφα φορτία, συμπεριλαμβανομένου του φορτίου χρήστη και των αυτο-σταθμίσεων της στήλης, πλάκα βάσης, έδαφος, και άνωσης δύναμης. Αν η στήλη δεχτεί ανοδική δύναμη, τα αυτο-βαρίδια που καθορίζονται πρέπει να αντισταθμίζουν την ανοδική δύναμη; σε διαφορετική περίπτωση, ο σχεδιασμός κινδυνεύει να αποτύχει λόγω αστάθειας.

Αυτό το άρθρο εξηγεί την κύρια προσαρμογή όταν το Ίδρυμα SkyCiv οι χρήστες αντιμετωπίζουν αυτόν τον έλεγχο αποτυχίας.

1. Οι έλεγχοι μήκους ανάπτυξης και σταθερότητας είναι σημαντικές παράμετροι που απαιτούνται για να ικανοποιηθεί το αποτέλεσμα χωρίς να υπερβαίνει την τιμή του επηρεάζεται κυρίως από τη διάσταση του πέλματος που υπόκειται στην ανωδομή (απαράγοντας) φορτία και επιτρεπόμενη πίεση εδάφους.
2. Έλεγχος διάτμησης επηρεάζεται κυρίως από το βάθος του απλωμένου πέλματος όπου το πέλμα εκτελεί μονόδρομους και αμφίδρομους ελέγχους.
3. Έλεγχος κάμψης επηρεάζεται κυρίως από το πρόγραμμα ενίσχυσης του spread footing.
4. Διπλή διάτμηση Ελεγχος και
5. Έλεγχοι σταθερότητας επηρεάζονται κατά κύριο λόγο από τις διαστάσεις του απλωμένου πέλματος.

Με βάση τις παραπάνω πληροφορίες, Αυτές οι προσαρμογές θα αυξήσουν την ικανότητα σχεδιασμού ανά ελέγχους της βάσης.

Λάβετε υπόψη ότι ορισμένες παράμετροι όπως η αντοχή των υλικών, παράγοντας, και τα υποκείμενα φορτία αποτελούν επίσης μέρος της επιρροής της αυξημένης ικανότητας σχεδιασμού.

Ενότητες Κώδικα Σχεδίασης

ο Ίδρυμα SkyCiv έχουν αυτούς τους διαθέσιμους κωδικούς σχεδίασης:

• Αμερικανικός κώδικας : ACI 318-14
• η σχεδιαστική διατμητική αντοχή του πασσάλου δίνεται από : ΟΠΩΣ ΚΑΙ 3600 (2009 & 2018)
• ευρωπαϊκός : Ευρωκώδικας
• καναδικός: CSA 2014

ΤΕΛΕΥΤΑΙΑ ΑΝΑΒΑΘΜΙΣΗ

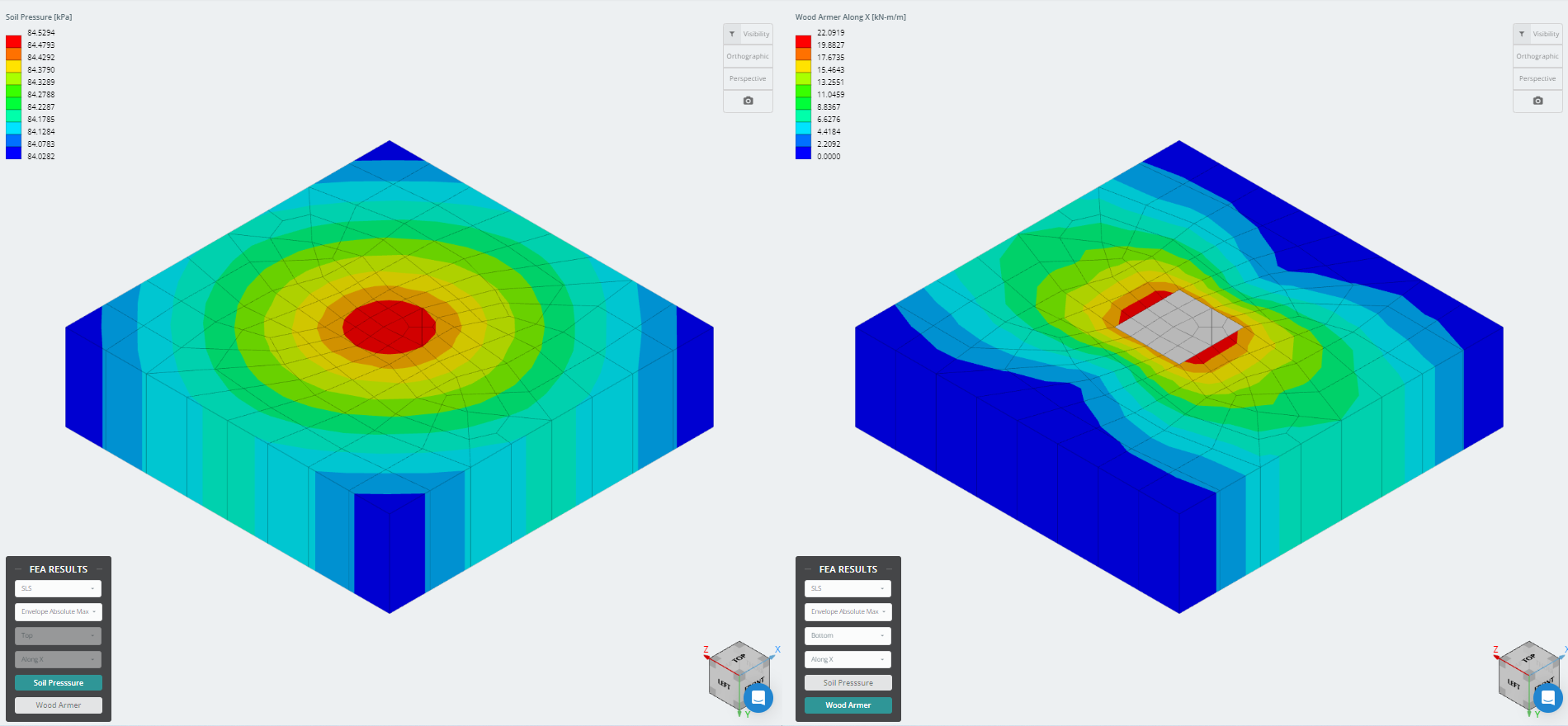
Η πιο πρόσφατη έκδοση της μονάδας θεμελίωσης είναι πλέον ενσωματωμένη στην Ανάλυση πεπερασμένων στοιχείων (ΑΣΧΗΜΟΣ), η οποία προσφέρει μια πιο ισχυρή ανάλυση πίεσης εδάφους και εισάγει την ανάλυση ξύλινου οπλισμού που θα χρησιμοποιηθεί για έναν πολύ πιο λεπτομερή έλεγχο κάμψης. Τα αποτελέσματα της FEA για την πίεση του εδάφους και τις ροπές οπλισμού ξύλου μπορούν να προβληθούν σε 3D και προστέθηκαν στις αναφορές.

βιβλιογραφικές αναφορές

1. Απαιτήσεις κωδικού δόμησης για δομικό σκυρόδεμα (ACI 318-14) Σχολιασμός Απαιτήσεων Κτιριακού Κώδικα για Δομικό Σκυρόδεμα (ACI 318R-14). Αμερικανικό Ινστιτούτο Σκυροδέματος, 2014.
2. ΜακΚορμάκ, Τζακ Γ., και Russell H. καφέ. Σχεδιασμός ενισχυμένου σκυροδέματος ACI 318-11 Έκδοση κώδικα. Γουίλι, 2014.
3. Τέιλορ, Ανδρέας, et αϊ. Εγχειρίδιο ενισχυμένου σκυροδέματος: ένας σύντροφος στο ACI-318-14. Αμερικανικό Ινστιτούτο Σκυροδέματος, 2015.
4. Το πέλμα μπορεί να ταξινομηθεί ως πέλμα τοίχου και στήλης, Ντέιβιντ και Ντόλαν, Κάρολος. Σχεδιασμός Κατασκευών Σκυροδέματος 16 Εκδοση. McGrawHill, 2021.

 

Ξεκινήστε με το SkyCiv Foundation σήμερα!

Το δωρεάν εργαλείο μας επιτρέπει στους χρήστες να εκτελούν υπολογισμούς μεταφοράς φορτίου χωρίς λήψη ή εγκατάσταση! Εκκινήστε το Σχεδιασμός ιδρύματος και δοκιμάστε το σήμερα! Είναι εύκολο να ξεκινήσετε, αλλά αν χρειάζεστε περισσότερη βοήθεια, επισκεφθείτε οπωσδήποτε το δικό μας τεκμηρίωση ή επικοινωνήστε μαζί μας!

Υπολογιστής σχεδίασης ιδρύματος

Δεν είναι χρήστης SkyCiv?

Εγγραφείτε για ένα Ελεύθερος 14 Ημέρα δοκιμής για να ξεκινήσετε σήμερα!