Πώς να υπολογίσετε τις αξονικές δυνάμεις ενός συστήματος ζευκτόντων χρησιμοποιώντας τη μέθοδο των αρθρώσεων?
Σε αυτό το σεμινάριο, θα εξηγήσουμε πώς να χρησιμοποιήσουμε τη μέθοδο των αρμών για τον υπολογισμό των εσωτερικών δυνάμεων των μελών σε ένα σύστημα δοκών ή κατασκευή.
Αυτές οι δυνάμεις είναι γνωστές ως αξονικές δυνάμεις και είναι πολύ σημαντικές στην ανάλυση ζευκτόντων. Εάν δεν είστε σαφείς σχετικά με το τι φαίνεται το χάος στο άρθρο μας – Τι είναι ένα ζευκτόν. Η μέθοδος των αρθρώσεων περιλαμβάνει βασικά την εξέταση κάθε μιας από τις «αρθρώσεις’ (όπου συναντιούνται τα μέλη) και εφαρμογή στατικών εξισώσεων για επίλυση.
Το σπουδαίο είναι, Προσθήκη απεριόριστων σημείων φορτίων το κάνει αυτόματα για εσάς. Μοντελοποιήστε τα δικά σας ζευκτά και το λογισμικό θα δείξει διαδραστική βήμα προς βήμα επεξεργασία της μεθόδου των αρμών!
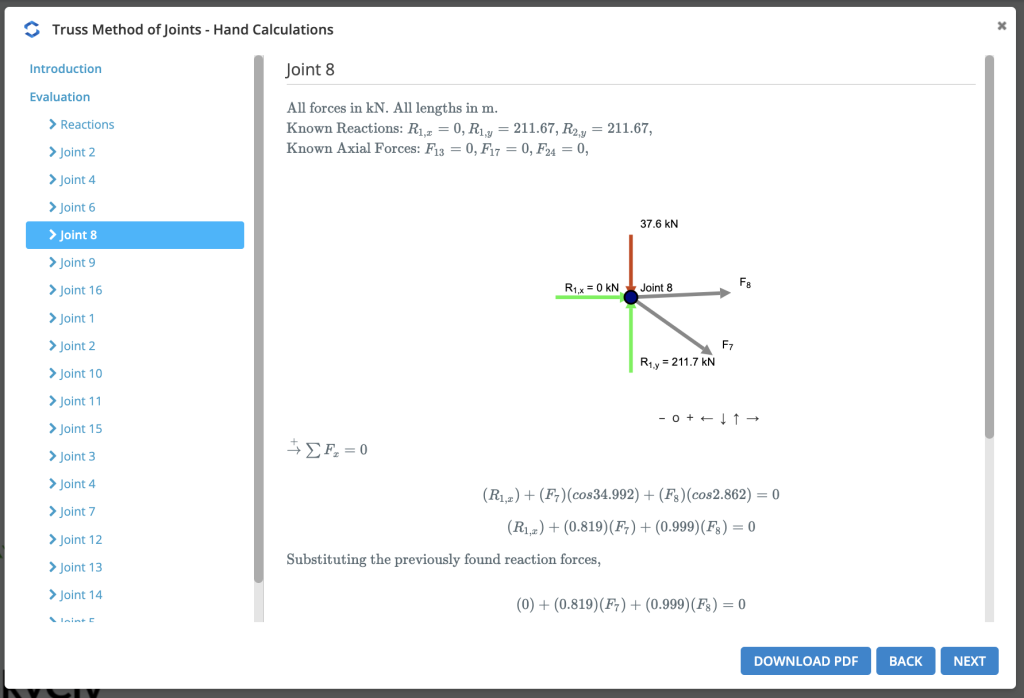
Βήμα 1: Υπολογίστε τις αντιδράσεις στα υποστηρίγματα
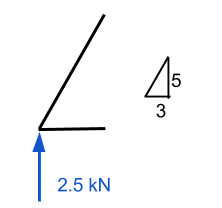
Πρώτα, υπολογίζουμε το αντιδράσεις στα στηρίγματα. Θα ξεκινήσουμε κοιτάζοντας ένα απλό παράδειγμα α 5 σύστημα δοκών μέλους:
Για να υπολογίσετε το στιγμή κάμψης σε αυτό το σύστημα ζευκτών, παίρνουμε πρώτα το άθροισμα των στιγμών στην αριστερή αντίδραση να είναι μηδέν. Το κάνουμε αυτό αγνοώντας όλα τα μέλη και κοιτάζοντας απλώς τις δυνάμεις και τα στηρίγματα στη δομή. Αυτό είναι το ίδιο με τη μέθοδο που χρησιμοποιήθηκε στο Bending Moment Reactions στο προηγούμενο σεμινάριό μας.
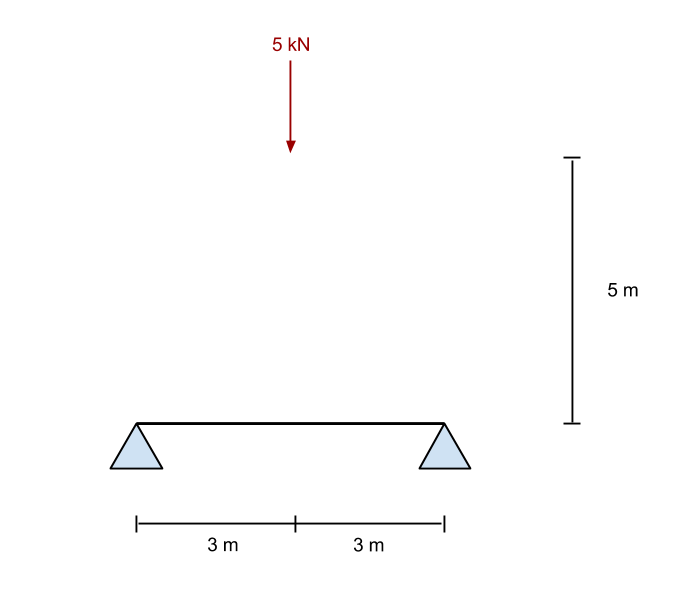
Από τις παραπάνω εξισώσεις, επιλύουμε τη δύναμη αντίδρασης στο σημείο Β (η σωστή υποστήριξη). Στο παράδειγμά μας, αυτό φαίνεται να είναι 2.5 kN σε ανοδική κατεύθυνση. Τώρα, αν πάρουμε το άθροισμα των δυνάμεων στο y (κατακόρυφος) κατεύθυνση, βρίσκουμε ότι η υποστήριξη Α (την αριστερή υποστήριξη) δίνεται επίσης ως 2.5 ΚΝ.
Βήμα 2: Εξετάστε ένα από τα υποστηρίγματα:
Τώρα που έχουμε τις δυνάμεις αντίδρασης, μπορούμε να ξεκινήσουμε την ανάλυση της υπόλοιπης δομής δοκών. Πρώτα, κοιτάζουμε μια από τις γνωστές δυνάμεις μας – σε αυτήν την περίπτωση, θα εξετάσουμε την αριστερή αντίδραση υποστήριξης του +2.5 ΚΝ. Εφόσον γνωρίζουμε ότι αυτή η δύναμη εμφανίζεται σε αυτό το σημείο, θα εξετάσουμε μόνο αυτό το σημείο μεμονωμένα. Επαναλαμβάνουμε αυτήν τη διαδικασία πολλές φορές, οπότε είναι σημαντικό να εξασκηθείτε και να μάθετε τη διαδικασία προκειμένου να έχετε καλή κατανόηση του τρόπου επίλυσης αξονικών δυνάμεων σε δομές δοκών. Και πάλι, σκεφτείτε το πρώτο σημείο στην υποστήριξη:
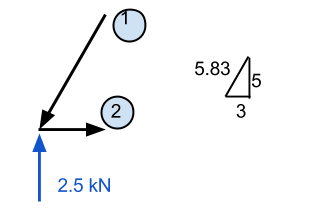
Μεγέθυνση σε αυτό το σημείο, βλέπουμε όλες τις γνωστές δυνάμεις να ενεργούν σε αυτό το σημείο. Από στατική, γνωρίζουμε ότι οι δυνάμεις στην κατεύθυνση x και y πρέπει να αθροιστούν στο μηδέν. Αναλόγως, αν γνωρίζουμε ότι υπάρχει μια ανοδική κάθετη δύναμη, τότε πρέπει να υπάρχει μια καθοδική δύναμη για να την αντισταθμίσει. Εφόσον έχουμε ήδη την αξία μιας δύναμης προς τα πάνω, τότε θα προσπαθήσουμε να αξιολογήσουμε τον αριθμό μέλους 1 πρώτα.
Εδώ απαιτούμε λίγη γνώση των διανυσμάτων. Είναι σημαντικό να θυμόμαστε ότι όλες οι δυνάμεις πρέπει να αθροίζονται στο μηδέν και για την κατεύθυνση x και y. Στο παράδειγμά μας, η οριζόντια απόσταση είναι 3m ενώ η κατακόρυφη είναι 5m – αφήνοντας μας με την υποτίναση ίση με περίπου 5.83 Μ. Χρησιμοποιώντας αυτό, μπορούμε να συμπεράνουμε ότι η συνιστώσα κανονικής δύναμης του μέλους 1 είναι ίσο με (5.83)/(5) φορές την κατακόρυφη δύναμη του 2.5 ΚΝ. Αυτό ισοδυναμεί με 2.92 Το kN και ΠΡΕΠΕΙ να είναι μια δύναμη προς τα κάτω αν το θέμα είναι να παραμείνει ακίνητος.
Μέλος 2 μπορεί να υπολογιστεί με τον ίδιο τρόπο. Αν γνωρίζουμε αυτό το μέλος 1 ενεργεί προς τα κάτω, τότε ξέρουμε ότι πρέπει επίσης να ενεργεί προς τα αριστερά. Αναλόγως, ξέρουμε μέλος 2 πρέπει να δημιουργεί μια δύναμη που τραβά το σημείο προς τα δεξιά για να διατηρήσει τις δυνάμεις στην κατεύθυνση x. Αυτή η τιμή υπολογίζεται από (3/5.83) Χ 2.92 kN και ισούται με 1.51 ΚΝ.
Βήμα 3: Μετάβαση σε άλλο σημείο:
Έχοντας υπολογίσει τις εσωτερικές δυνάμεις του πρώτου μέλους στη δοκό μας, θα κοιτάξουμε τώρα ένα άλλο σημείο για να επαναλάβουμε τη διαδικασία:
Πάλι, θα μεγεθύνουμε το σημείο αναφοράς και θα εξετάσουμε όλες τις γνωστές δυνάμεις που δρουν στο σημείο:
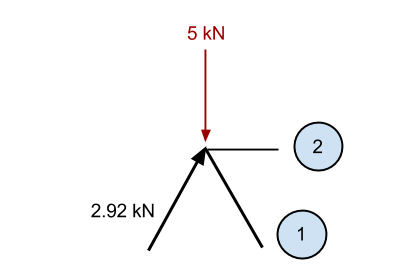
Με τον ίδιο τρόπο όπως και πριν, εάν αθροίσουμε το γνωστό κάθετο συστατικό του 2.92 μέλος kN (2.5 kN στην κατακόρυφη κατεύθυνση) και το – 5kN προς τα κάτω δύναμη, τότε έχουμε υπερβολική κατεύθυνση προς τα κάτω 2.5 ΚΝ (5 – 2.5). Αναλόγως, ξέρουμε αυτό το μέλος 1 πρέπει να προκαλεί δύναμη προς τα πάνω να διατηρήσει το σημείο στατικό. Αυτή η δύναμη πρέπει να έχει ένα κατακόρυφο συστατικό του 2.5 ΚΝ, και αφού είναι στην ίδια γωνία με το προηγούμενο μέλος, τότε η εσωτερική αξονική δύναμη πρέπει επίσης να είναι 2.92 ΚΝ.
Τώρα εξετάζουμε τις δυνάμεις στην κατεύθυνση x. Σε αυτό το σημείο, όλη η κάθετη δύναμη από το μέλος 1 αντιστέκεται στην κατακόρυφη δύναμη του προηγουμένως υπολογισμένου μέλους. Αυτό σημαίνει ότι το άθροισμα των δυνάμεων στην κατεύθυνση x είναι ήδη μηδέν. Αναλόγως, δεν μπορεί να υπάρξει δύναμη στο Μέλος 2 αλλιώς το σημείο θα γίνει ανισορροπημένο και δεν θα είναι πλέον στατικό.
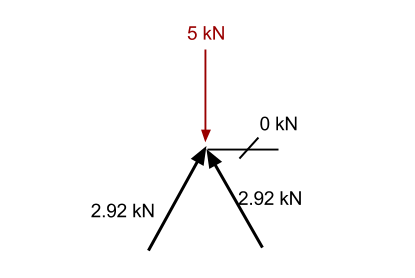
Βήμα 4: Μετάβαση σε άλλο σημείο:
Κοιτάζοντας αυτό το σημείο, μπορούμε να δούμε ότι υπάρχει μια ειδική περίπτωση. Σε αυτή την κατάσταση, οποιαδήποτε δύναμη που σπρώχνει προς τα πάνω δεν θα έχει καμία πιθανή αντίσταση δράση, καθώς δεν υπάρχει άλλο μέλος που να μπορεί να παρέχει μια καθοδική δύναμη για να διατηρήσει το σημείο στατικό. Αναλόγως, αφού το άθροισμα των δυνάμεων πρέπει να είναι μηδέν, αυτό το μέλος δεν μπορεί να έχει καμία δύναμη που να σχετίζεται με αυτό. Το, επομένως, δεν έχει δύναμη σε αυτό και είναι γνωστό ως μηδενικό μέλος.
Πάλι, αν κοιτάξουμε το άθροισμα των δυνάμεων στην κατεύθυνση x, μπορούμε να δούμε ότι υπάρχει μόνο ένα μέλος που έχει οποιαδήποτε δύναμη στην κατεύθυνση x. Αναλόγως, αυτό πρέπει επίσης να έχει 0 αξονική δύναμη ώστε το άθροισμα των δυνάμεων να είναι ίσο με μηδέν.
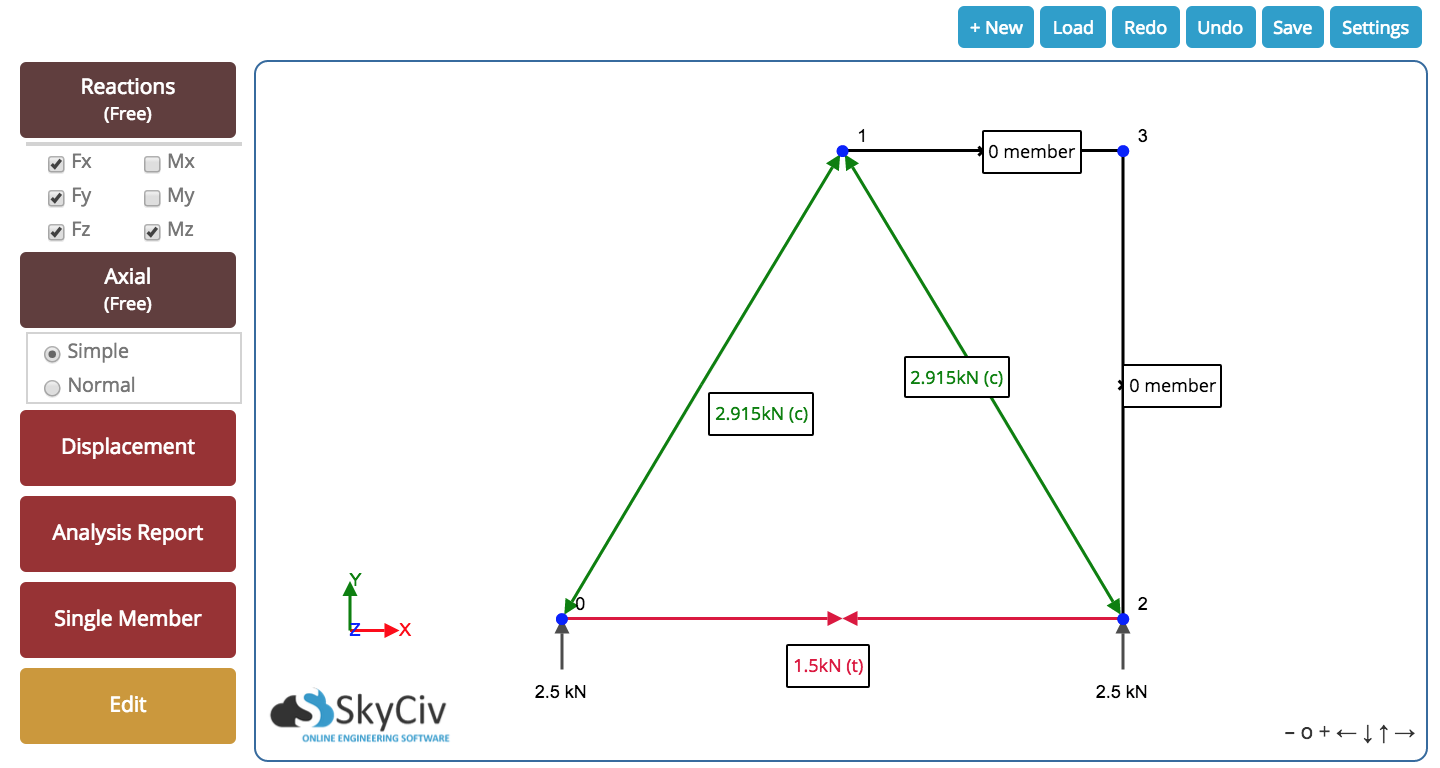
ΤΕΛΙΚΗ λυση
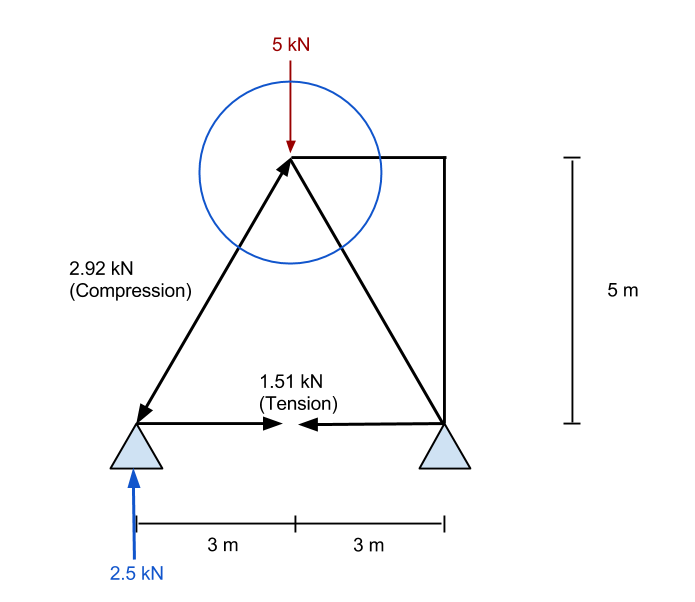
Τελικά, καταλήγουμε με το ακόλουθο αποτέλεσμα για το ζευκτόν μας. Μπορούμε να δούμε όλες τις προκύπτουσες αξονικές δυνάμεις μέσα στο μέλος και το αντιδράσεις στα στηρίγματα. Το ακόλουθο αποτέλεσμα λήφθηκε από το δικό μας Δωρεάν Υπολογιστής ζευκτόντων – δοκίμασέ το, είναι δωρεάν!
Απλά βήματα
- Ξεκινήστε πάντα υπολογίζοντας τις αντιδράσεις σε υποστηρίγματα
- Διαλέξτε ένα σημείο με γνωστή δύναμη και κοιτάξτε το μεμονωμένα
- Χρησιμοποιήστε τη διανυσματική γεωμετρία και το άθροισμα των δυνάμεων = 0 για να λύσει τις άλλες δυνάμεις-μέλη
- Επαναλάβετε τη διαδικασία μέχρι να λυθούν όλα τα μέλη
- Θυμηθείτε να προσέξετε τα Μηδενικά Μέλη
Σχετικό φροντιστήριο
- Επίλυση ζευκτών με μέθοδο τμημάτων. Περιλαμβάνει βίντεο και οδηγό βήμα προς βήμα
Προσθήκη απεριόριστων σημείων φορτίων
Προσθήκη απεριόριστων σημείων φορτίων μπορεί να υπολογίσει τη μέθοδο των αρθρώσεων αυτόματα για εσάς. Ή δοκιμάστε το δικό μας Δωρεάν Υπολογιστής ζευκτόντων που θα σου δώσει την τελική απάντηση (χωρίς υπολογισμούς με το χέρι).
Για να εξερευνήσετε περισσότερη λειτουργικότητα του λογισμικού SkyCiv, εγγραφείτε σήμερα για να ξεκινήσετε!
