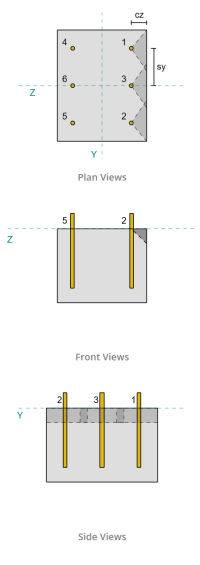
Παράδειγμα σχεδιασμού πλάκας βάσης χρησιμοποιώντας AISC 360-22 και ACI 318-19
Προβληματική δήλωση
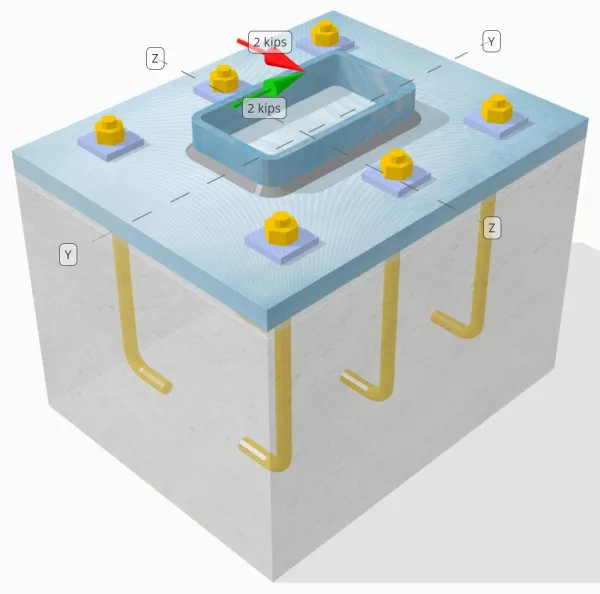
Προσδιορίστε εάν η σχεδιασμένη σύνδεση στήλης-πλάκας βάσης είναι επαρκής για α Vy=2-kip και Vz=2-kip φορτία διάτμησης.
Δεδομένα
Στήλη:
Ενότητα στήλης: HSS7X4X5/16
Επιφάνεια στήλης: 7.59 σε2
Υλικό στήλης: A36
Πλάκα βάσης:
Διαστάσεις πλάκας βάσης: 12 σε x 14 σε
Πάχος πλάκας βάσης: 3/4 σε
Υλικό πλάκας βάσης: A36
Πηκτώ:
Πάχος ενέματος: 0.25 σε
Σκυρόδεμα:
Διαστάσεις σκυροδέματος: 12 σε x 14 σε
Πάχος σκυροδέματος: 10 σε
Σκυρόδεμα: 3000 psi
Ραγισμένα ή αδιευκρίνιστα: Ραγισμένος
Άγκυρες:
Διάμετρος άγκυρας: 1/2 σε
Αποτελεσματικό μήκος ενσωμάτωσης: 8 σε
Πάχος πλυντηρίου πιάτων: 0.25 σε
Σύνδεση πλυντηρίου πιάτων: Συγκολλημένο σε πλάκα βάσης
Συγκολλήσεις:
Μέγεθος συγκόλλησης: 1/4 σε
Η ταξινόμηση μετάλλων πλήρωσης: Ε70ΧΧ
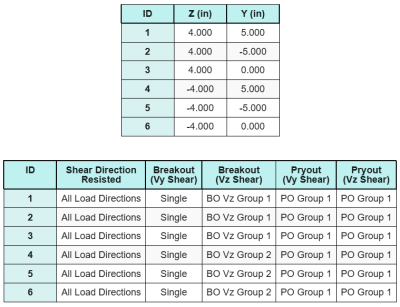
Δεδομένα αγκυροβόλησης (από Υπολογιστής Skyciv):
Μοντέλο στο δωρεάν εργαλείο SkyCiv
Μοντελοποιήστε το παραπάνω σχέδιο πλάκας βάσης χρησιμοποιώντας το δωρεάν διαδικτυακό μας εργαλείο σήμερα! Δεν απαιτείται εγγραφή.
Ορισμοί
Διαδρομή φόρτωσης:
Ο σχεδιασμός ακολουθεί τις συστάσεις του Οδηγός σχεδίασης AISC 1, 3έκδοση, και ACI 318-19. Τα διατμητικά φορτία που εφαρμόζονται στη στήλη μεταφέρονται στην πλάκα βάσης μέσω των συγκολλήσεων, και στη συνέχεια στο σκυρόδεμα στήριξης μέσω του ράβδοι αγκύρωσης. Οι ωτίδες τριβής και διάτμησης δεν λαμβάνονται υπόψη σε αυτό το παράδειγμα, καθώς αυτοί οι μηχανισμοί δεν υποστηρίζονται στο τρέχον λογισμικό.
Από προεπιλογή, η εφαρμοζόμενη Το διατμητικό φορτίο κατανέμεται σε όλες τις αγκυρώσεις, είτε με τη χρήση συγκολλημένων πλακών πλακών είτε με άλλα μηχανικά μέσα. Το φορτίο που μεταφέρει κάθε άγκυρα προσδιορίζεται χρησιμοποιώντας τα τρία (3) περιπτώσεις που αναφέρονται σε ACI 318-19 Ρήτρα 17.7.2 και Σχ. R17.7.2.1b. Στη συνέχεια, κάθε άγκυρα μεταφέρει το φορτίο στο σκυρόδεμα στήριξης από κάτω. Η κατανομή φορτίου σύμφωνα με αυτές τις αναφορές χρησιμοποιείται επίσης κατά τον έλεγχο της διατμητικής αντοχής του χάλυβα αγκύρωσης για να εξασφαλιστεί η συνέχεια στις παραδοχές μεταφοράς φορτίου.
Ως εναλλακτική, το λογισμικό επιτρέπει μια απλοποιημένη και πιο συντηρητική υπόθεση, όπου ολόκληρο το διατμητικό φορτίο εκχωρείται μόνο στο αγκυρώσεις πλησιέστερα στο φορτωμένο άκρο. Σε αυτήν την περίπτωση, ο έλεγχος διατμητικής ικανότητας εκτελείται μόνο σε αυτές τις αγκυρώσεις άκρων.
Ομάδες άγκυρας:
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV Περιλαμβάνει ένα διαισθητικό χαρακτηριστικό που προσδιορίζει ποιες άγκυρες αποτελούν μέρος μιας ομάδας αγκύρωσης για αξιολόγηση διάτμηση σκυροδέματος και διάτμηση σκυροδέματος αποτυχία.
Ενα ομάδα άγκυρας ορίζεται ως δύο ή περισσότερες άγκυρες με επικαλυπτόμενες περιοχές προβαλλόμενης αντίστασης. Σε αυτήν την περίπτωση, οι άγκυρες δρουν μαζί, και η συνδυασμένη αντίστασή τους ελέγχεται έναντι του εφαρμοζόμενου φορτίου στην ομάδα.
ΕΝΑ μονή άγκυρα ορίζεται ως μια άγκυρα της οποίας η περιοχή προβαλλόμενης αντίστασης δεν επικαλύπτεται με καμία άλλη. Σε αυτήν την περίπτωση, η άγκυρα ενεργεί μόνη της, και η εφαρμοζόμενη διατμητική δύναμη σε αυτή την άγκυρα ελέγχεται απευθείας έναντι της ατομικής της αντίστασης.
Αυτή η διάκριση επιτρέπει στο λογισμικό να καταγράφει τόσο τη συμπεριφορά της ομάδας όσο και την ατομική απόδοση αγκύρωσης κατά την αξιολόγηση των τρόπων αστοχίας που σχετίζονται με τη διάτμηση.
Υπολογισμοί βήμα προς βήμα
Ελεγχος #1: Υπολογίστε τη χωρητικότητα συγκόλλησης
Το πρώτο βήμα είναι ο υπολογισμός του Συνολικό μήκος συγκόλλησης διαθέσιμο για αντίσταση στη διάτμηση. Δεδομένου ότι η πλάκα βάσης είναι συγκολλημένη κατά μήκος της περιμέτρου του τμήματος της στήλης, το συνολικό μήκος συγκόλλησης προκύπτει αθροίζοντας τις συγκολλήσεις σε όλες τις πλευρές.
\( ΜΕΓΑΛΟ_{συγκόλληση} = 2 \αριστερά( αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{διάσελο} – 2r_{διάσελο} – 2αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{διάσελο} \σωστά) + 2 \αριστερά( ρε_{διάσελο} – 2r_{διάσελο} – 2αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{διάσελο} \σωστά) \)
\( ΜΕΓΑΛΟ_{συγκόλληση} = 2 \φορές (4\,\κείμενο{σε} – 2 \φορές 0,291,κείμενο{σε} – 2 \φορές 0,291,κείμενο{σε}) + 2 \φορές (7\,\κείμενο{σε} – 2 \φορές 0,291,κείμενο{σε} – 2 \φορές 0,291,κείμενο{σε}) = 17.344,κείμενο{σε} \)
Χρησιμοποιώντας αυτό το μήκος συγκόλλησης, οι εφαρμοζόμενες διατμητικές δυνάμεις στο y- και οι κατευθύνσεις z χωρίζονται για να προσδιοριστεί ο μέσος όρος διατμητική δύναμη ανά μονάδα μήκους προς κάθε κατεύθυνση:
\( v_{uy} = frac{V_y}{ΜΕΓΑΛΟ_{συγκόλληση}} = frac{2\,\κείμενο{δέρμα μόσχου ακατέργαστου}}{17.344\,\κείμενο{σε}} = 0,11531,κείμενο{kip/in} \)
\( v_{να} = frac{V_z}{ΜΕΓΑΛΟ_{συγκόλληση}} = frac{2\,\κείμενο{δέρμα μόσχου ακατέργαστου}}{17.344\,\κείμενο{σε}} = 0,11531,κείμενο{kip/in} \)
ο προκύπτουσα διάτμηση ζήτηση ανά μονάδα μήκους στη συνέχεια προσδιορίζεται χρησιμοποιώντας την τετραγωνική ρίζα του αθροίσματος των τετραγώνων (SRSS) μέθοδος.
\( r_u = sqrt{(v_{uy})^ 2 + (v_{να})^ 2} \)
\( r_u = sqrt{(0.11531\,\κείμενο{kip/in})^ 2 + (0.11531\,\κείμενο{kip/in})^ 2} = 0,16308,κείμενο{kip/in} \)
Επόμενο, η χωρητικότητα συγκόλλησης υπολογίζεται χρησιμοποιώντας AISC 360-22 Εξ. J2-4, με τον συντελεστή κατευθυντικής αντοχής λαμβανόμενο ως kds=1,0 για ένα τμήμα HSS. Η χωρητικότητα συγκόλλησης για α 1/4 στη συγκόλληση καθορίζεται ως:
\( \phi r_n = phi 0.6 ΦΑ_{Exx} E_w k_{δδ} = 0.75 \φορές 0.6 \φορές 70,κείμενο{ksi} \φορές 0,177,κείμενο{σε} \φορές 1 = 5,5755,κείμενο{kip/in} \)
Είναι επίσης απαραίτητο να ελέγξετε τα βασικά μέταλλα, τόσο η στήλη όσο και η πλάκα βάσης, χρησιμοποιώντας AISC 360-22 Εξ. J4-4 για να ληφθεί η αντοχή σε διάτμηση. Αυτό δίνει:
\( \phi r_{nbm, διάσελο} = phi 0.6 ΦΑ_{u_col} αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{διάσελο} = 0.75 \φορές 0.6 \φορές 58,κείμενο{ksi} \φορές 0,291,κείμενο{σε} = 7,5951,κείμενο{kip/in} \)
\( \phi r_{nbm, bp} = phi 0.6 ΦΑ_{u_bp} αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{bp} = 0.75 \φορές 0.6 \φορές 58,κείμενο{ksi} \φορές 0,75,κείμενο{σε} = 19.575,κείμενο{kip/in} \)
\( \phi r_{nbm} = minαριστερά( \phi r_{nbm, bp},\, \phi r_{nbm, διάσελο} \σωστά) = min(19.575\,\κείμενο{kip/in},\, 7.5951\,\κείμενο{kip/in}) = 7,5951,κείμενο{kip/in} \)
Δεδομένου ότι η πραγματική τάση συγκόλλησης είναι μικρότερη από τις χωρητικότητες τόσο των μετάλλων όσο και των βασικών μετάλλων συγκόλλησης, 0.16308 KPI < 5.5755 kpi και 0.16308 KPI < 7.5951 KPI, η σχεδιαστική χωρητικότητα συγκόλλησης είναι επαρκής.
Ελεγχος #2: Υπολογίστε την ικανότητα διάσπασης σκυροδέματος λόγω διάτμησης Vy
Χωρητικότητα κάθετου άκρου:

Από τη διάταξη, Άγκυρες 1 και 4 είναι πιο κοντά στην άκρη και έχουν το μικρότερη απόσταση περίπου 1. Χρησιμοποιώντας αυτές τις τιμές ca1 για την προβολή των κώνων αστοχίας, το λογισμικό αναγνώρισε αυτές τις άγκυρες ως άγκυρες, αφού οι προβαλλόμενοι κώνοι τους δεν επικαλύπτονται. Η υποστήριξη ήταν επίσης αποφασισμένη να μην είναι στενό μέλος, οπότε η απόσταση ca1 χρησιμοποιείται απευθείας χωρίς τροποποίηση.
Ας υπενθυμίσουμε ότι η δύναμη διάτμησης θεωρείται ότι κατανέμεται μεταξύ όλων των αγκυρίων. Ο υπολογισμός για το Με διατμητικό φορτίο εφαρμόζεται σε κάθε μεμονωμένη άγκυρα:
\( V_{faperp} = frac{V_y}{n_a} = frac{2\,\κείμενο{δέρμα μόσχου ακατέργαστου}}{6} = 0,33333,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Ας αναλογιστούμε Αγκυρα 1. Η μέγιστη προβαλλόμενη περιοχή μιας άγκυρας υπολογίζεται χρησιμοποιώντας ACI 318-19 Εξ. 17.7.2.1.3.
\( ΕΝΑ_{Vco} = 4.5 (ντο_{a1, s1})💕⬛ Αγορά Indocin από 4.5 \φορές (2\,\κείμενο{σε})^2 = 18,κείμενο{σε}^ 2 \)
Στη συνέχεια, η πραγματική προβαλλόμενη περιοχή προσδιορίζεται από το πλάτος και το ύψος του προβαλλόμενου κώνου αστοχίας.
\( ΣΙ_{Vc} = min(ντο_{αριστερά,s1},\, 1.5ντο_{a1, s1}) + \ελάχ(ντο_{σωστά,s1},\, 1.5ντο_{a1, s1}) \)
\( ΣΙ_{Vc} = min(10\,\κείμενο{σε},\, 1.5 \φορές 2,κείμενο{σε}) + \ελάχ(2\,\κείμενο{σε},\, 1.5 \φορές 2,κείμενο{σε}) = 5,κείμενο{σε} \)
\( η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Vc} = min(1.5ντο_{a1, s1},\, αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{σύμπλεγμα}) = min(1.5 \φορές 2,κείμενο{σε},\, 10\,\κείμενο{σε}) = 3,κείμενο{σε} \)
\( ΕΝΑ_{Vc} = B_{Vc} η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Vc} = 5,κείμενο{σε} \φορές 3,κείμενο{σε} = 15,κείμενο{σε}^ 2 \)
Το επόμενο βήμα είναι η χρήση Εξισώσεις 17.7.2.2.1a και 17.7.2.2.1b για να υπολογίσετε τη βασική δύναμη διάσπασης μιας μόνο άγκυρας. Ως μικρότερη τιμή λαμβάνεται η ικανότητα διακυβέρνησης.
\( V_{β1} = 7 \αριστερά( \frac{\ελάχ(ο,\, 8d_a)}{d_a} \σωστά)^{0.2} \τ.μ.{\frac{d_a}{\κείμενο{σε}}} \lambda_a sqrt{\frac{f'_c}{\κείμενο{psi}}} \αριστερά( \frac{ντο_{a1, s1}}{\κείμενο{σε}} \σωστά)^{1.5} \,\κείμενο{lbf} \)
\( V_{β1} = 7 \φορές αριστερά( \frac{\ελάχ(8\,\κείμενο{σε},\, 8 \φορές 0,5,κείμενο{σε})}{0.5\,\κείμενο{σε}} \σωστά)^{0.2} \φορές sqrt{\frac{0.5\,\κείμενο{σε}}{1\,\κείμενο{σε}}} \φορές 1 \φορές sqrt{\frac{3\,\κείμενο{ksi}}{0.001\,\κείμενο{ksi}}} \φορές αριστερά( \frac{2\,\κείμενο{σε}}{1\,\κείμενο{σε}} \σωστά)^{1.5} \φορές 0,001,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( V_{β1} = 1,1623,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( V_{β2} = 9 \lambda_a sqrt{\frac{f'_c}{\κείμενο{psi}}} \αριστερά( \frac{ντο_{a1, s1}}{\κείμενο{σε}} \σωστά)^{1.5} \,\κείμενο{lbf} \)
\( V_{β2} = 9 \φορές 1 \φορές sqrt{\frac{3\,\κείμενο{ksi}}{0.001\,\κείμενο{ksi}}} \φορές αριστερά( \frac{2\,\κείμενο{σε}}{1\,\κείμενο{σε}} \σωστά)^{1.5} \φορές 0,001,κείμενο{δέρμα μόσχου ακατέργαστου} = 1,3943,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( V_b = min(V_{β1},\, V_{β2}) = min(1.1623\,\κείμενο{δέρμα μόσχου ακατέργαστου},\, 1.3943\,\κείμενο{δέρμα μόσχου ακατέργαστου}) = 1,1623,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Επόμενο, ο παραμέτρους ικανότητας διάσπασης καθορίζονται. ο παράγοντας επίδρασης άκρης διάσπασης υπολογίζεται σύμφωνα με ACI 318-19 Ρήτρα 17.7.2.4, και το συντελεστής πάχους υπολογίζεται σύμφωνα με Ρήτρα 17.7.2.6.1.
\( \Psi_{εκδ,Β} = minαριστερά(1.0,\, 0.7 + 0.3 \αριστερά( \frac{ντο_{a2,s1}}{1.5ντο_{a1, s1}} \σωστά) \σωστά) = minαριστερά(1,\, 0.7 + 0.3 \φορές αριστερά( \frac{2\,\κείμενο{σε}}{1.5 \φορές 2,κείμενο{σε}} \σωστά) \σωστά) = 0.9 \)
\( \Psi_{η,Β} = maxαριστερά( \τ.μ.{ \frac{1.5ντο_{a1, s1}}{αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{σύμπλεγμα}} },\, 1.0 \σωστά) = maxαριστερά( \τ.μ.{ \frac{1.5 \φορές 2,κείμενο{σε}}{10\,\κείμενο{σε}} },\, 1 \σωστά) = 1 \)
Τελικά, ACI 318-19 Ρήτρα 17.7.2.1(ένα) χρησιμοποιείται για τον προσδιορισμό της ικανότητας διάσπασης σκυροδέματος μιας μονής άγκυρας σε διάτμηση. Η υπολογιζόμενη ικανότητα για διάτμηση Vy στην κάθετη διεύθυνση είναι 0.69 kips .
\( \phi V_{cbperp} = phi αριστερά( \frac{ΕΝΑ_{Vc}}{ΕΝΑ_{Vco}} \σωστά) \Psi_{εκδ,Β} \Psi_{ντο,Β} \Psi_{η,Β} V_b \)
\( \phi V_{cbperp} = 0.65 \φορές αριστερά( \frac{15\,\κείμενο{σε}^ 2}{18\,\κείμενο{σε}^ 2} \σωστά) \φορές 0.86 \φορές 1 \φορές 1 \φορές 1,1623,κείμενο{δέρμα μόσχου ακατέργαστου} = 0,56661,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Η υπολογιζόμενη χωρητικότητα για Με διάτμηση στο κάθετος κατεύθυνση είναι 0.56 kips .
Χωρητικότητα παράλληλης ακμής:
Σε αυτό το σενάριο είναι επίσης δυνατή η αστοχία κατά μήκος της άκρης παράλληλα με το φορτίο, έτσι το ικανότητα διάσπασης σκυροδέματος για την παράλληλη άκρη πρέπει να καθοριστεί. Οι αγκυρώσεις ή η ομάδα αγκύρωσης που λαμβάνονται υπόψη είναι εκείνες που ευθυγραμμίζονται με την παράλληλη άκρη. συνεπώς, ο ca1 Η απόσταση άκρου μετράται από την άγκυρα μέχρι την άκρη κατά μήκος της κατεύθυνσης Z. Με βάση το παρακάτω σχήμα, οι προβολές του κώνου αστοχίας επικαλύπτονται; επομένως, οι άγκυρες αντιμετωπίζονται ως ομάδα.
Υπόθεση 1:

Υπόθεση 2:

Αναφερόμαστε σε ACI 318-19 Σύκο. R17.7.2.1b για τις διαφορετικές περιπτώσεις που χρησιμοποιούνται κατά την αξιολόγηση των ομάδων αγκύρωσης. Σε αυτό το σχέδιο πλάκας βάσης, συγκολλημένες ροδέλες πλακών χρησιμοποιούνται ειδικά. Επομένως, μόνο Υπόθεση 2 ελέγχεται.
Το απαιτούμενο φορτίο για την ομάδα αγκύρωσης στο Case 2 λαμβάνεται ως το συνολικό διατμητικό φορτίο.
\( V_{faπαράλληλος,περίπτωση 2} = V_y = 2,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Στον υπολογισμό της χωρητικότητας για την Περίπτωση 2 αποτυχία, οι άγκυρες που εξετάζονται είναι οι πίσω άγκυρες. Σαν άποτέλεσμα, η απόσταση ακμής ca1 μετριέται από την πίσω ομάδα αγκύρωσης μέχρι την άκρη αστοχίας.
Με αυτήν την απόσταση ca1 και τον προσανατολισμό των άκρων, πρέπει να επαληθευτεί εάν η υποστήριξη πληροί τις προϋποθέσεις ως στενό μέλος. Εξής ACI 318-19 Ρήτρα 17.7.2.1.2, το λογισμικό SkyCiv Base Plate προσδιόρισε την υποστήριξη ως στενός. Επομένως, ο τροποποιημένη απόσταση ca1 χρησιμοποιείται, που υπολογίζεται ότι είναι 6.667 σε.
Ακολουθούνται τα ίδια βήματα όπως στην κάθετη περίπτωση: υπολογισμός του προβλεπόμενες περιοχές αστοχίας, ο βασική δύναμη διάσπασης μονής άγκυρας, και το παραμέτρους διάσπασης. Οι υπολογισμένες τιμές για κάθε βήμα φαίνονται παρακάτω.
\( ΕΝΑ_{Vco} = 4.5 (ντο_{«a1,g2})💕⬛ Αγορά Indocin από 4.5 \φορές (6.6667\,\κείμενο{σε})^2 = 200,κείμενο{σε}^ 2 \)
\( ΕΝΑ_{Vc} = B_{Vc} η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Vc} = 14,κείμενο{σε} \φορές 10,κείμενο{σε} = 140,κείμενο{σε}^ 2 \)
\( V_{β1} = 7,0733,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( V_{β2} = 8,4853,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( V_b = min(V_{β1},\, V_{β2}) = min(7.0733\,\κείμενο{δέρμα μόσχου ακατέργαστου},\, 8.4853\,\κείμενο{δέρμα μόσχου ακατέργαστου}) = 7,0733,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( \Psi_{εκδ,Β} = 1.0 \)
\( \Psi_{η,Β} = 1.0 \)
Η εξίσωση για την χωρητικότητα της παράλληλης ακμής διαφέρει από την χωρητικότητα της κάθετης ακμής. ACI 318-19 Ρήτρα 17.7.2.1(ντο) εφαρμόζεται, όπου είναι η εξίσωση διάσπασης πολλαπλασιάζεται επί 2.
\( \phi V_{cbgπαράλληλο} = 2 \φι αριστερά( \frac{ΕΝΑ_{Vc}}{ΕΝΑ_{Vco}} \σωστά) \Psi_{εκδ,Β} \Psi_{ντο,Β} \Psi_{η,Β} V_b \)
\( \phi V_{cbgπαράλληλο} = 2 \φορές 0.65 \φορές αριστερά( \frac{140\,\κείμενο{σε}^ 2}{200\κείμενο{σε}^ 2} \σωστά) \φορές 1 \φορές 1 \φορές 1 \φορές 7,0733,κείμενο{δέρμα μόσχου ακατέργαστου} = 6,4367,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Η υπολογιζόμενη χωρητικότητα για Με διάτμηση στο παράλληλο κατεύθυνση είναι 6.43 kips .
Τώρα αξιολογούμε τις κάθετες και τις παράλληλες αστοχίες ξεχωριστά.
- Για την αστοχία της κάθετης ακμής, Από 0.33 δέρμα μόσχου ακατέργαστου < 0.56 δέρμα μόσχου ακατέργαστου, η ικανότητα διάτμησης σκυροδέματος σχεδιασμού είναι επαρκής.
- Για την αστοχία παράλληλης ακμής, Από 2 δέρμα μόσχου ακατέργαστου < 6.43 δέρμα μόσχου ακατέργαστου, η ικανότητα διάτμησης σκυροδέματος σχεδιασμού είναι επαρκής.
Ελεγχος #3: Υπολογίστε την ικανότητα διάσπασης σκυροδέματος λόγω διάτμησης Vz
Η πλάκα βάσης υπόκειται επίσης σε Vz διάτμηση, οπότε πρέπει να ελεγχθούν οι ακμές αστοχίας κάθετες και παράλληλες προς τη διάτμηση Vz. Χρησιμοποιώντας την ίδια προσέγγιση, οι κάθετες και παράλληλες χωρητικότητες υπολογίζονται ως 2.45 kips και 1.26 kips , αντίστοιχα.
Κάθετη ακμή:

Παράλληλη ακμή:

Στη συνέχεια, αυτές οι ικανότητες συγκρίνονται με τις απαιτούμενες δυνάμεις.
- Για την αστοχία της κάθετης ακμής, Από 2 δέρμα μόσχου ακατέργαστου < 2.45 δέρμα μόσχου ακατέργαστου, η ικανότητα διάτμησης σκυροδέματος είναι επαρκής.
- Για την αστοχία παράλληλης ακμής, Από 0.33 δέρμα μόσχου ακατέργαστου < 1.26 δέρμα μόσχου ακατέργαστου, η ικανότητα διάτμησης σκυροδέματος είναι επαρκής.
Ελεγχος #4: Υπολογίστε την ικανότητα εκτόξευσης σκυροδέματος
ο κώνος σκυροδέματος για αστοχία εκροής είναι ο ίδιος κώνος που χρησιμοποιείται στον έλεγχο διάσπασης εφελκυσμού. Για τον υπολογισμό της ικανότητας διάτμησης, πρέπει πρώτα να προσδιοριστεί η ονομαστική αντοχή θραύσης σε εφελκυσμό των μονών αγκυρίων ή της ομάδας αγκύρωσης. Οι λεπτομερείς υπολογισμοί για τον έλεγχο διάσπασης εφελκυσμού καλύπτονται ήδη στο Παραδείγματα σχεδίασης SkyCiv για φορτίο τάσης.

Είναι σημαντικό να σημειωθεί ότι ο προσδιορισμός της ομάδας αγκύρωσης για διάτμηση διάτμησης είναι διαφορετικός από αυτόν για τη διάτμηση. Επομένως, οι αγκυρώσεις στο σχέδιο πρέπει να ελέγχονται ακόμη για να διαπιστωθεί εάν υποκρίνομαι έχω ένα ομάδα ή ως άγκυρες έναντι της αστοχίας διάτμησης. Η ταξινόμηση της υποστήριξης ως α στενό τμήμα πρέπει επίσης να επαληθεύεται και να ακολουθεί τις ίδιες συνθήκες που χρησιμοποιούνται ξέσπασμα έντασης.
Από τους υπολογισμούς SkyCiv, ο ονομαστική αντοχή σε εφελκυσμό της ομάδας αγκύρωσης είναι 12.772 kips . Με συντελεστή ανάκρισης του kcp=2, η χωρητικότητα του σχεδιασμού είναι:
\( \phi V_{cpg} = hy k_{cp} Ν_{cbg} = 0.65 \φορές 2 \φορές 12.772 \,\κείμενο{δέρμα μόσχου ακατέργαστου} = 16.604,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Η απαιτούμενη δύναμη είναι η αποτέλεσμα των εφαρμοζόμενων διατμητικών φορτίων. Αφού όλες οι άγκυρες ανήκουν σε μια ενιαία ομάδα, η συνολική προκύπτουσα διάτμηση εκχωρείται στην ομάδα.
\( V_{κάνω} = sqrt{(V_y)^ 2 + (V_z)^ 2} = sqrt{(2\,\κείμενο{δέρμα μόσχου ακατέργαστου})^ 2 + (2\,\κείμενο{δέρμα μόσχου ακατέργαστου})^ 2} = 2,8284,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( V_{κάνω} = αριστερά( \frac{V_{κάνω}}{n_a} \σωστά) n_{ένα,G1} = αριστερά( \frac{2.8284\,\κείμενο{δέρμα μόσχου ακατέργαστου}}{6} \σωστά) \φορές 6 = 2,8284,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Επειδή το συνολικό διατμητικό φορτίο είναι μικρότερο από την ικανότητα της ομάδας αγκύρωσης, 2.82 kips < 18.976 kips , η χωρητικότητα του σχεδιασμού είναι επαρκής.
Ελεγχος #5: Υπολογίστε την ικανότητα διάτμησης της ράβδου αγκύρωσης
Θυμηθείτε ότι σε αυτό το παράδειγμα σχεδίασης, Η διάτμηση κατανέμεται σε όλες τις άγκυρες. Το συνολικό διατμητικό φορτίο ανά άγκυρα είναι επομένως το αποτέλεσμα του μεριδίου του στο φορτίο Vy και του μεριδίου του στο φορτίο Vz.
\( v_{κάνω,και} = frac{V_y}{n_a} = frac{2\,\κείμενο{δέρμα μόσχου ακατέργαστου}}{6} = 0,33333,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( v_{κάνω,με} = frac{V_z}{n_a} = frac{2\,\κείμενο{δέρμα μόσχου ακατέργαστου}}{6} = 0,33333,κείμενο{δέρμα μόσχου ακατέργαστου} \)
\( V_{κάνω} = sqrt{(v_{κάνω,και})^ 2 + (v_{κάνω,με})^ 2} \)
\( V_{κάνω} = sqrt{(0.33333\,\κείμενο{δέρμα μόσχου ακατέργαστου})^ 2 + (0.33333\,\κείμενο{δέρμα μόσχου ακατέργαστου})^ 2} = 0,4714,κείμενο{δέρμα μόσχου ακατέργαστου} \)
Αυτό δίνει το διατμητική τάση στη ράβδο αγκύρωσης όπως και:
\( f_v = frac{V_{κάνω}}{ΕΝΑ_{ράβδος}} = frac{0.4714\,\κείμενο{δέρμα μόσχου ακατέργαστου}}{0.19635\,\κείμενο{σε}^ 2} = 2,4008,κείμενο{ksi} \)
Επειδή υπάρχει πλυντήριο πιάτων, ένα έκκεντρο διατμητικό φορτίο επάγεται στη ράβδο αγκύρωσης. Η εκκεντρότητα λαμβάνεται ως το ήμισυ της απόστασης που μετριέται από την κορυφή του στηρίγματος σκυροδέματος έως το κέντρο της ροδέλας πλακών, λαμβάνοντας υπόψη το πάχος της πλάκας βάσης. Παραπέμπω Οδηγός σχεδίασης AISC 1, 3Ενότητα rd Edition 4.3.3.
\( ε = 0.5 \αριστερά( \frac{αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{pw}}{2} + αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{bp} \σωστά) = 0.5 \φορές αριστερά( \frac{0.25\,\κείμενο{σε}}{2} + 0.75\,\κείμενο{σε} \σωστά) = 0,4375,κείμενο{σε} \)
Η ροπή από την έκκεντρη διάτμηση εκφράζεται στη συνέχεια ως α αξονική τάση στη ράβδο αγκύρωσης. Χρησιμοποιώντας το συντελεστή τομής, η αξονική τάση λόγω αυτής της ροπής υπολογίζεται ως:
\( Z_{ράβδος} = frac{\πι}{32} (d_a)^3 = frac{\πι}{32} \φορές (0.5\,\κείμενο{σε})^3 = 0,012272,κείμενο{σε}^ 3 \)
\( f_t = frac{V_{κάνω} μι}{Z_{ράβδος}} = frac{0.4714\,\κείμενο{δέρμα μόσχου ακατέργαστου} \φορές 0,4375,κείμενο{σε}}{0.012272\,\κείμενο{σε}^ 3} = 16.806,κείμενο{ksi} \)
Διατμητική ικανότητα ράβδου αγκύρωσης ACI:
Εξής ACI 318-19 Ρήτρα 17.7.1, Στη συνέχεια προσδιορίζεται η αντοχή σχεδιασμού. ΕΝΑ 0.8 συντελεστής μείωσης εφαρμόζεται λόγω της παρουσίας του επιθέματα ενέματος. Η σχεδιαστική ικανότητα είναι επομένως:
\( \phi V_{προς την,εδώ} = 0.8 \phi 0.6 ΕΝΑ_{Ξέρω,β} φά_{Γιούτα} = 0.8 \φορές 0.65 \φορές 0.6 \φορές 0,1419κείμενο{σε}^2 φορές 90κείμενο{ksi} = 3,9845κείμενο{δέρμα μόσχου ακατέργαστου} \)
Ως εναλλακτική, ο Λογισμικό SkyCiv Base Plate επιτρέπει την 0.8 να απενεργοποιηθεί η απλοποίηση, και χρησιμοποιήστε το πραγματικό πάχος του μαξιλαριού ενέματος στους υπολογισμούς. Σε αυτήν την περίπτωση, η συνολική εκκεντρότητα περιλαμβάνει το επίθεμα ενέματος, και η συνδυασμένη διατμητική και αξονική αντοχή προσδιορίζεται σύμφωνα με τις διατάξεις του AISC.
Διατμητική ικανότητα ράβδου αγκύρωσης AISC:
Πρώτα, ο ονομαστικές τάσεις διάτμησης και εφελκυσμού καθορίζονται για ράβδο Α325.
\( ΦΑ_{nv} = 0.45 ΦΑ_{εσύ,Α.Κ.} = 0.45 \φορές 120\ \κείμενο{ksi} = 54\ \κείμενο{ksi} \)
\( ΦΑ_{nt} = 0.75 ΦΑ_{εσύ,Α.Κ.} = 0.75 \φορές 120\ \κείμενο{ksi} = 90\ \κείμενο{ksi} \)
Η μέθοδος AISC χρησιμοποιεί AISC 360-22 Εξ. J3-3a, που μπορεί να εκφραστεί ότι περιλαμβάνει τις επιπτώσεις της αξονικής τάσης. Αυτό πραγματοποιείται ως εξής.
\( ΦΑ'_{nv} = min αριστερά( 1.3 ΦΑ_{nv} – \αριστερά( \frac{ΦΑ_{nv}}{\Phi f_{nt}} \σωστά) f_t,\; ΦΑ_{nv} \σωστά) \)
\( ΦΑ'_{nv} = min αριστερά( 1.3 \φορές 54\ \κείμενο{ksi} – \αριστερά( \frac{54\ \κείμενο{ksi}}{0.75 \φορές 90\ \κείμενο{ksi}} \σωστά) \φορές 16.806\ \κείμενο{ksi},\; 54\ \κείμενο{ksi} \σωστά) = 54\ \κείμενο{ksi} \)
Η διατμητική ικανότητα σχεδιασμού από τη μέθοδο AISC υπολογίζεται στη συνέχεια ως:
\( \phi R_{ν,\μαθηματικά{aisc}} = phi F'_{nv} ΕΝΑ_{ράβδος} = 0.75 \φορές 54\ \κείμενο{ksi} \φορές 0.19635\ \κείμενο{σε}💕⬛ Αγορά Indocin από 7.9522\)
Για να διασφαλιστεί ότι καλύπτονται και οι δύο μέθοδοι, η ικανότητα διακυβέρνησης λαμβάνεται ως η μικρότερη από τις δύο, το οποίο είναι 3.98 δέρμα μόσχου ακατέργαστου.
\( \phi V_n = min αριστερά( \phi V_{προς την,εδώ},\; \phi R_{ν,\μαθηματικά{aisc}} \σωστά) = min (3.9845\ \κείμενο{δέρμα μόσχου ακατέργαστου},\; 7.9522\ \κείμενο{δέρμα μόσχου ακατέργαστου}) = 3.9845\ \κείμενο{δέρμα μόσχου ακατέργαστου} \)
Δεδομένου ότι το διατμητικό φορτίο ανά ράβδο αγκύρωσης είναι μικρότερο από τη χωρητικότητα της ράβδου αγκύρωσης σε διάτμηση, 0.47 δέρμα μόσχου ακατέργαστου < 3.98 δέρμα μόσχου ακατέργαστου, η σχεδιαστική ικανότητα διάτμησης της ράβδου αγκύρωσης είναι επαρκής.
Περίληψη σχεδίου
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV Μπορεί να δημιουργήσει αυτόματα μια αναφορά υπολογισμού βήμα προς βήμα για αυτό το παράδειγμα σχεδιασμού. Παρέχει επίσης μια περίληψη των επιταγών που εκτελούνται και των προκύπτουσων αναλογιών τους, καθιστώντας τις πληροφορίες κατανοητές με μια ματιά. Παρακάτω είναι ένας πίνακας συνοπτικών δείγματος, που περιλαμβάνεται στην αναφορά.
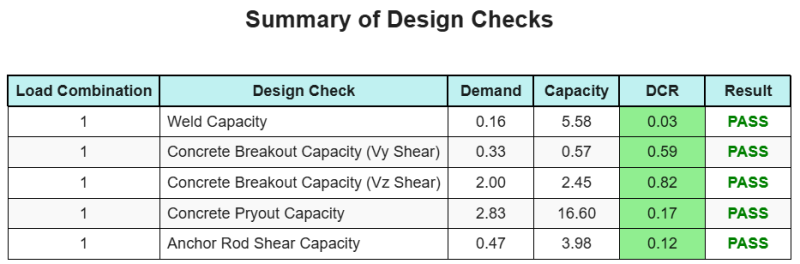
Αναφορά δείγματος SkyCIV
Δείτε το επίπεδο λεπτομέρειας και σαφήνειας που μπορείτε να περιμένετε από μια αναφορά σχεδίασης πλάκας βάσης SkyCiv. Η αναφορά περιλαμβάνει όλους τους βασικούς ελέγχους σχεδιασμού, εξισώσεις, και τα αποτελέσματα παρουσιάζονται σε σαφή και ευανάγνωστη μορφή. Είναι πλήρως συμβατό με τα πρότυπα σχεδιασμού. Κάντε κλικ παρακάτω για να προβάλετε ένα δείγμα αναφοράς που δημιουργήθηκε με χρήση του SkyCiv Base Plate Calculator.
Αγορά λογισμικού πλάκας βάσης
Αγοράστε την πλήρη έκδοση της μονάδας σχεδιασμού πλάκας βάσης από μόνη της χωρίς άλλες ενότητες SkyCIV. Αυτό σας δίνει ένα πλήρες σύνολο αποτελεσμάτων για σχεδιασμό πλάκας βάσης, συμπεριλαμβανομένων λεπτομερών αναφορών και περισσότερων λειτουργιών.