擁壁にかかる横土圧の計算

擁壁に作用する主な荷重の 1 つは横土圧です。. そんな理由で, コンクリート擁壁の設計においては、その規模と分布を適切に推定することが重要です。. 一般に, 壁が移動しようとする方向に応じて、横土圧には 3 つの異なるタイプがあります。:

• 静止土圧: 壁の動きが完全に拘束されたとき
• 有効土圧: 壁が残留土から離れる方向に傾く可能性がある場合
• パッシブ土圧: 壁が残留土に押し込まれる可能性がある場合

記事上で, 上記の土圧の場合のそれぞれの公式の説明に焦点を当てます。.

横方向土圧分布

一般に, 横土圧は静水圧と同じように作用します. 前述の 2 つの境界間の線形分布に従い、表面ではゼロ値、最深部では最大値を持ちます。. したがって, 水平地下応力分布は次の式で表されます。:

\(\sigma_h = K_* cdot (\ガンマ z)\)

どこ \(K_*) の値を取る \(K_o\) 静止圧の場合, \(K_a\) アクティブな圧力の場合, そして \(K_p\) 受動的圧力の場合.

からの横方向の地下応力の与えられた式を統合する \(0\) に \(H\) に \(z), 結果は次のようになります:

\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)

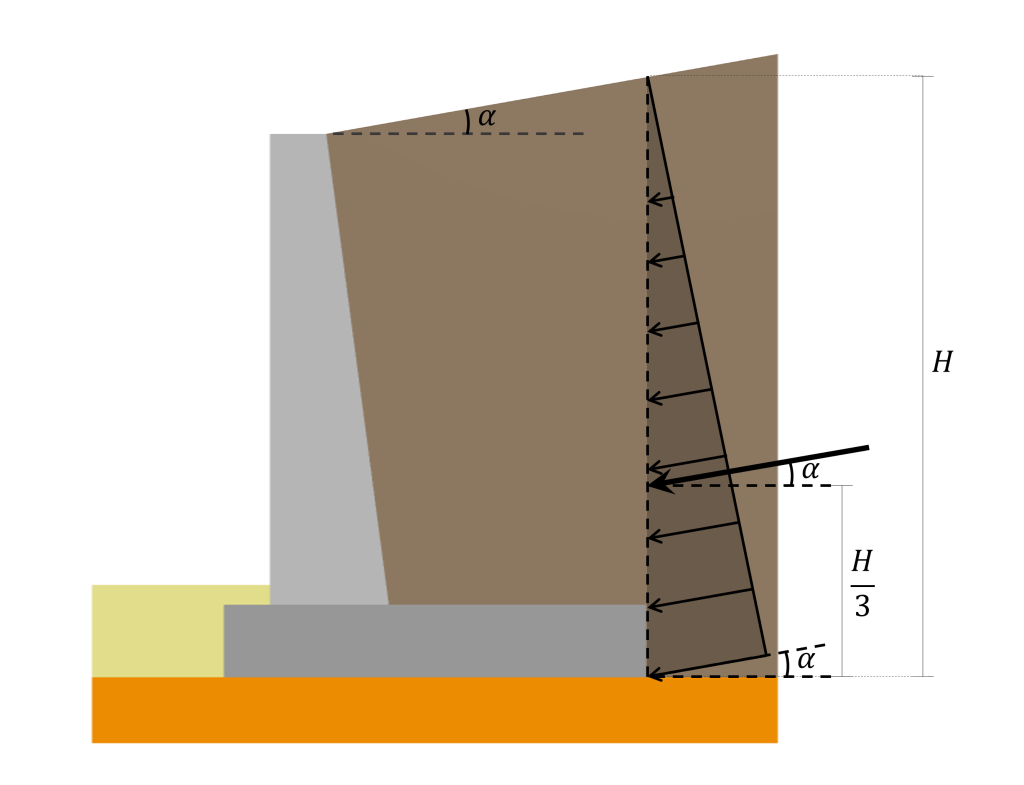
この結果の行動線は次のとおりです。 \(\フラク{2}{3}H\) 表面から. 横方向の土圧分布, その結果として生じる, 上で説明した場所と場所を次の図に示します。:

提示された分布とその結果として得られる計算アプローチは、垂直背面に作用する土圧にのみ適用されることに言及することが重要です。. 背面が傾斜した擁壁の場合 (上の写真のように), 土圧が作用する表面は、ヒールの終点に位置する垂直面内で作用すると想定されるため、依然として垂直であるとみなされます。.

さらに, 埋め戻しがある角度で傾斜している場合 \(\alpha\) 水平方向に関して, 圧力分布とその合力は同じ角度で傾いている \(\alpha\) 以下に示すように:

横方向の土圧分布とその結果を正確に推定することは、擁壁設計プロセスにおける重要なステップです。. この側方土圧が擁壁設計プロセスにどのように含まれているかについての詳細は、, 記事参照 ここに. それでは、さまざまな条件で土壌によって擁壁にかかる合成横土圧を計算する式を見てみましょう。.

静止時横土圧

擁壁に対する横方向の土圧を計算するためのこのアプローチは、擁壁が完全に静止しており、土壌から離れたり土壌の中に移動したりすることが許可されていない場合にのみ使用できます。, この条件により、土壌の水平ひずみは確実にゼロになります。. この場合, 静止圧力係数 (\(K_o\)) 代わりになるものです \(K_*) 前の式では. この係数は、圧力分布とその結果を計算する上で唯一不明な点です。. 通常の固結土の場合, の関係 \(K_o\) です:

\(K_o = 1-罪(\ファイ)\)

どこ \(\ファイ) 考慮される土壌の有効摩擦角です。.

過固結土壌の場合, 係数は次の式を使用して計算できます。:

\(K_o = (1-それなし(\ファイ))\cdot OCR^{それなし(\ファイ)}\)

どこ \(\ファイ) は有効摩擦角です, そして \(OCR\) 土の過圧密率を考慮した.

この係数を静止時横土圧からの合力を求める式に代入すると、:

\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)

有効横土圧

前のアプローチは、壁がまったく降伏しない場合に使用できます。, しかしながら, 壁が土から離れる傾向がある場合, どの深さでも壁にかかる土圧は減少します. この場合, 有効圧力係数 (\(K_a\)) 代わりになるものです \(K_*) 初期方程式では. ランキンのアプローチを使用して、 粒状埋め戻し, そして、圧力が次のように作用すると仮定します。 垂直背面, 有効土圧係数は次の方程式を使用して計算できます。:

\(K_a=cos(\アルファ) \フラク{cos(\アルファ) – \平方根{cos^2(\アルファ) – cos^2(\ファイ)}}{cos(\アルファ) + \平方根{cos^2(\アルファ) – cos^2(\ファイ)}}\)

どこ \(\ファイ) は考慮される土壌の摩擦角であり、 \(\alpha\) 水平方向に対する埋め戻し面の傾斜角度です。.

この係数を活動状態での横土圧からの合力を計算する式に代入すると、次のようになります。:

\(P_a=frac{1}{2} \ガンマ cdot H^2 cdot K_a)

前に示したランキンのアクティブ圧力の計算は、壁に摩擦がないという仮定に基づいています。.

受動的横土圧

擁壁に作用する横方向の土圧は、擁壁が土塊に押し込まれるときに受動的であるとみなされます。, その状態で, 水平応力は静止状態に比べて増加します. この場合, 受動圧力係数 (\(K_p\)) 代わりになるものです \(K_*) 初期方程式では. ランキンのアプローチを使用して、 粒状埋め戻し, そして、圧力が次のように作用すると仮定します。 垂直背面, 受動土圧係数は次の式を使用して計算できます。:

埋め戻しが完全に水平になった場合

\(K_p = Tan^2(45º+\frac{\ファイ}{2})\)

埋め戻しが水平に対してある角度だけ傾いている場合

\(K_p=cos(\アルファ) \フラク{cos(\アルファ) + \平方根{cos^2(\アルファ) – cos^2(\ファイ)}}{cos(\アルファ) – \平方根{cos^2(\アルファ) – cos^2(\ファイ)}}\)

どこ \(\ファイ) は考慮される土壌の摩擦角であり、 \(\alpha\) 水平方向に対する埋め戻し面の傾斜角度です。.

この係数を受動的状態での横土圧からの合力を計算する式に代入すると、次のようになります。:

\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)

再び, 前に示したランキンのアクティブ圧力の計算は、壁に摩擦がないという仮定に基づいています。.

参考文献

擁壁計算機

SkyCivは、壁の側方土圧を計算する無料の擁壁計算機を提供します, 擁壁の安定性分析を実行します. の場合、ベースの下部から壁の高さの半分, の場合、ベースの下部から壁の高さの半分, 転倒に対する擁壁の安定性を計算する方法, スライディング, とベアリング!

擁壁計算機