Come calcolare un raggio indeterminato – Metodo doppio integrale
Indeterminato travi può essere una sfida a causa dei passaggi aggiuntivi necessari per risolvere le reazioni. Ricorda che le strutture indeterminate hanno quello che viene chiamato un grado di indeterminatezza. Per risolvere la struttura, devono essere introdotte condizioni al contorno. conseguentemente, maggiore è il grado di indeterminatezza, le condizioni più al contorno devono essere identificate. Ma prima di poter risolvere un raggio indeterminato, dobbiamo prima identificare se il raggio è staticamente indeterminato. Poiché le travi sono strutture unidimensionali, è sufficiente utilizzare l'equazione per determinare strutture esternamente staticamente indeterminate.
[matematica]
io_{e}= R- sinistra ( 3+e_{c} \giusto )
[matematica]
Dove:
- ioe = Grado di indeterminatezza
- R = Numero totale di reazioni
- ec = Condizioni esterne (per esempio. cerniera interna)
Generalmente, però, senza la necessità di risolvere il grado di indeterminazione, qualsiasi cosa diversa da semplici campate o travi a sbalzo sono staticamente indeterminate, supponendo che tali travi non siano dotate di cerniere interne.
Ci sono molti modi per affrontare si tratta di risolvere i fasci indeterminati. Anche se per semplicità e somiglianza con SkyCiv Beam's calcoli a mano, discuteremo il metodo della doppia integrazione.
Doppia integrazione
La doppia integrazione è forse il più semplice di tutti i metodi per l'analisi delle travi. Il concetto di questo metodo è piuttosto semplice rispetto ad altri metodi poiché si basa principalmente su una comprensione di base del calcolo integrale, da qui il nome. Un po 'di calcolo integrale viene adattato dalla relazione della curvatura della trave al momento mostrato di seguito.
[matematica]
\frac{1}{\rho}= Frac{M}{NO}
[matematica]
Notare che 1 / ρ è la curvatura del raggio e che ρ è il raggio della curva. fondamentalmente, la definizione di curvatura è la velocità di variazione della tangente rispetto alla lunghezza dell'arco. Poiché il momento è funzione del carico rispetto alla lunghezza dell'asta, integrando la curvatura rispetto alla lunghezza dell'elemento si otterrà l'inclinazione della trave. Allo stesso modo, integrando la pendenza rispetto alla lunghezza dell'elemento si otterrà la deflessione della trave. Poiché i carichi strutturali tipici sono di natura algebrica, l'integrazione di queste espressioni è semplice come usare la formula della potenza generale.
[matematica]
\int f sinistra ( x destra )^{n}dx = frac{f sinistra ( x destra )^{n + 1}}{n + 1}+C
[matematica]
Forse il modo migliore per comprendere il concetto è fornire un esempio di trave con quanto segue.
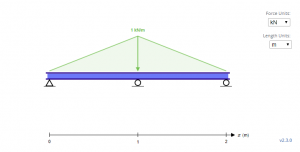
La trave campione sopra è una trave indeterminata con carichi triangolari. Con il supporti, Ay, By e Cy per la prima, secondo, e terzo supporto rispettivamente, il primo passo per risolvere queste incognite è iniziare con le equazioni di equilibrio.
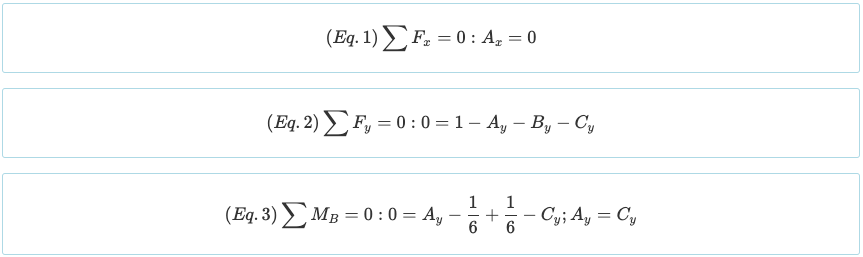
Si noti che il raggio ha un grado di indeterminazione statica di 1°. Poiché ci sono quattro incognite (Ax, Ay, By, e Cy) e ci sono tre equazioni così lontane dalle equazioni di equilibrio di cui sopra, è necessario creare un'altra equazione dalle condizioni al contorno. Ricordiamo che i momenti generati da un carico puntuale e da un carico triangolare sono i seguenti.
Punto di carico:
[matematica]
M = F volte x; M = Fx
[matematica]
Carico triangolare:
[matematica]
M = frac{w_{0}\volte x}{2}\volte sinistra ( \frac{x}{3} \giusto ); M = frac{w_{0}x ^{2}}{6}
[matematica]
Utilizzando il metodo della doppia integrazione, queste nuove equazioni vengono create e visualizzate di seguito.

Nota: Le equazioni di cui sopra sono scritte come funzioni di Macaulay in cui un'espressione è uguale a zero quando x < L. In questo caso, L = 1.
Nelle equazioni precedenti, si noti che il quarto termine aggiunto sembra spuntare dal nulla. Infatti, la direzione del carico è opposta alla direzione di gravità. Ciò è dovuto al fatto che le equazioni per i carichi triangolari funzionano solo quando il carico è crescente all'aumentare della lunghezza. Questo non è un gran problema per le equazioni distribuito e punti di carico per la loro simmetria. In effetti, il carico equivalente per la trave sopra è simile alla trave sottostante, quindi le equazioni sono basate su di esso.
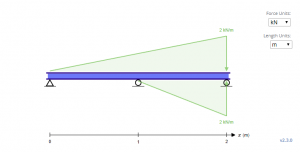
Per risolvere per C1 e C2, le condizioni al contorno devono essere determinate. Nella trave sopra, si può osservare che esistono tre di tali condizioni al contorno x = 0, x = 1, e x = 2, dove la deflessione y è zero nelle tre posizioni.
Condizione al contorno 1
[matematica]
x = 0, y = 0; C_{2}= 0
[matematica]
Condizione al contorno 2
[matematica]
x = 0, y = 0; C_{1}= Frac{1}{120}-\frac{UN_{y}}{6}
[matematica]
Dopo aver determinato i valori di ciascuna costante, l'ultima equazione può ora essere ottenuta utilizzando l'ultima condizione al contorno.
Condizione al contorno 3
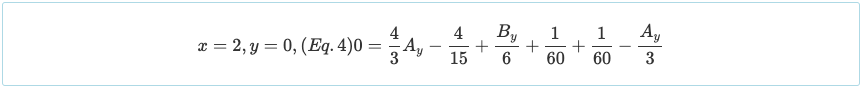
Notare che la condizione al contorno di θ = 0 in x = 1 può essere utilizzata, sebbene sia applicabile solo per la reazione intermedia di una trave continua simmetrica con carico simmetrico.
Poiché le quattro equazioni sono state determinate, ora possono essere risolti simultaneamente. La risoluzione di queste equazioni produrrà le seguenti reazioni.

Con le reazioni determinate, i valori delle reazioni possono essere sostituiti di nuovo all'equazione del momento. Questo ci permetterà di determinare il valore del momento in qualsiasi parte del sistema di travi.
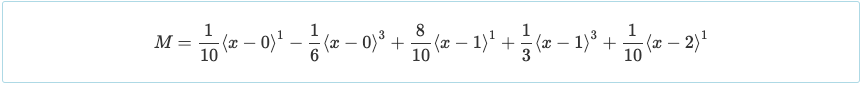
Un'altra comodità della doppia integrazione è che l'equazione del momento è presentata in un modo che può essere utilizzato per risolvere il taglio con la relazione mostrata di seguito.
[matematica]
V = frac{dM}{dx}
[matematica]
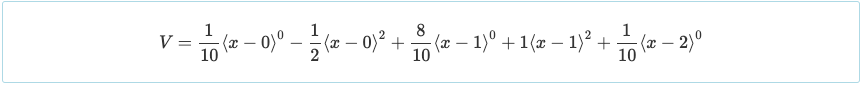
Ancora una volta, utilizzando solo una conoscenza di base del calcolo differenziale, equiparando la derivata di una funzione a zero si ottiene il massimo o il minimo di quella funzione. così, che equivale a V = 0 risulterà in un momento massimo positivo a x = 0.447 e x = 1.553 di M = 0.030

Ovviamente, tutto questo può essere verificato con SkyCiv Beam.
Software SkyCiv Beam
Software di analisi del raggio SkyCiv consente agli utenti di analizzare le strutture delle travi in modo semplice e accurato. È possibile ottenere un'analisi del membro della trave, Compreso reazioni, forza di taglio, momento flettente, la deflessione , e sottolinea in pochi secondi.
Se vuoi provalo prima, Calcolatore gratuito di travi è un ottimo modo per iniziare, o semplicemente registrati gratuitamente oggi!


