I fondamenti del centroide
È importante annotare questo su una sezione trasversale, la cui area è uniforme in tutto, il baricentro può essere trovato facendo la somma dei momenti rispetto ad un asse arbitrariamente impostato, ma di solito è impostato sulla fibra superiore o inferiore. Dai un'occhiata al nostro precedente articolo su come trovare il baricentro di una sezione di trave e calcolatore del centroide gratuito SkyCiv.
fondamentalmente, il baricentro può essere ottenuto sommando i momenti sulla sommatoria dell'area. Che si esprime in questo modo.
[matematica]
\bar{x}= Frac{1}{A}\int xf sinistra ( x destra )dx
[matematica]
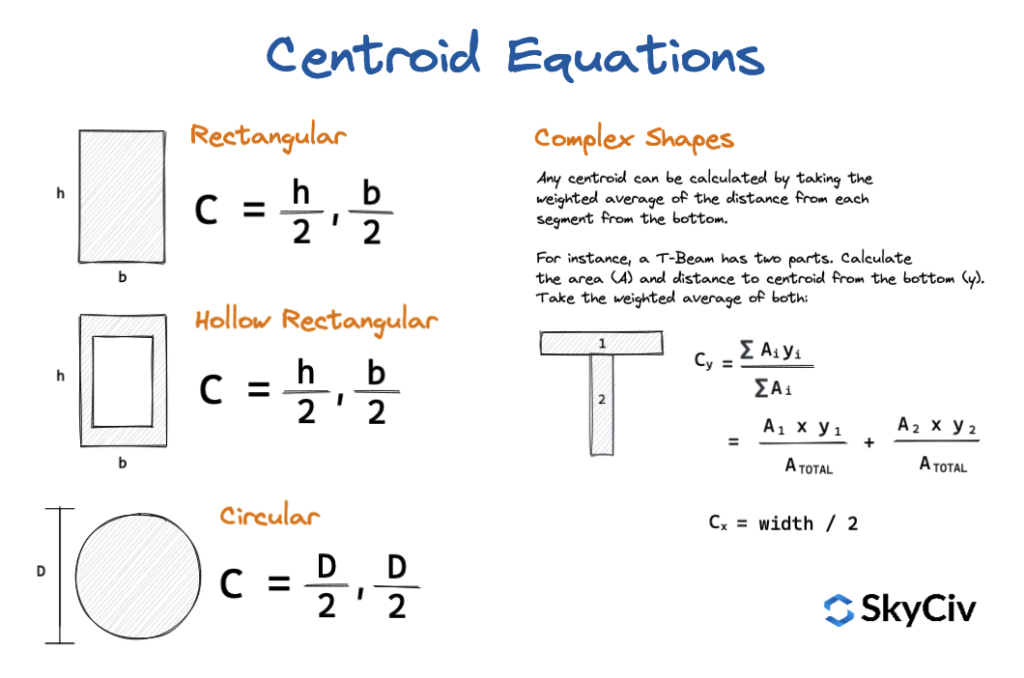
Riepilogo delle equazioni del centroide
Nell'equazione sopra, f(x) è la funzione ex è il braccio del momento. Per illustrare meglio questo, deriveremo il baricentro y di un triangolo arbitrario con la sua base coincidente con l'asse x. In questa situazione, la forma del triangolo, sia equilatero, isoscele o scalene è irrilevante poiché tutto è relativo solo all'asse x. Nota la forma è irrilevante se la base del triangolo è coincidente o parallela rispetto all'asse. Questo non sarà il caso quando si risolve per il centroide x. Anziché, puoi immaginarlo come ottenere il baricentro di due triangoli rettangoli rispetto all'asse y. Per comodità, immaginiamo un triangolo isoscele simile alla tabella di riferimento sottostante. Trovare la relazione tra b e h produrrà la seguente relazione.
[matematica]
\frac{-y}{x}= Frac{-h}{b}
[matematica]
Nota che la pendenza è negativa poiché immaginiamo che il triangolo sia verticale. Se immaginiamo che il triangolo sia invertito, la pendenza sarebbe positiva. Indipendentemente, il rapporto rimane lo stesso. Come x = f(y), la relazione di cui sopra può essere riscritta come segue.
[matematica]
x = f left ( y giusto )= Frac{b}{h}y
[matematica]
Ora possiamo risolvere il centroide. Regolazione della prima equazione sopra, otteniamo quanto segue.
[matematica]
\bar{y}= Frac{1}{A}\int yf sinistra ( y giusto )Due
[matematica]
L'inserimento di valori aggiuntivi e la sostituzione della relazione precedente produrrà la seguente equazione.
[matematica]
\bar{y}= Frac{2}{bh}\int_{0}^{h} \frac{b}{h}e ^{2}Due
[matematica]
Semplificare,
[matematica]
\bar{y}= Frac{2}{h ^{2}}\sinistra [ \frac{e ^{3}}{3} \giusto ]_{0}^{h}
[matematica]
[matematica]
\bar{y}= Frac{2}{h ^{2}}\sinistra [ \frac{h ^{3}}{3}-0 \giusto ]
[matematica]
[matematica]
\bar{y}= Frac{2}{3}h
[matematica]
Si noti che questa soluzione è presa dall'alto. Il baricentro preso dal basso deve quindi essere uguale a 1/3 di h.
Formula per centroidi di forme comuni e sezioni di travi
Di seguito è riportato un elenco di a varietà di forme della sezione della trave e la distanza dai baricentro della sezione. Le equazioni mostrano come trovare il baricentro di una particolare sezione dalla base o dal punto più a sinistra della sezione. Per abbonamenti SkyCiv Student e Structural, questo riferimento può anche essere scaricato come riferimento PDF da portare con te ovunque tu vada. I centroidi di una sezione di trave sono estremamente importanti in quanto individuano l'asse neutro e sono uno dei primi passaggi richiesti durante l'analisi di una sezione di trave.
SkyCiv offre anche un riepilogo completo della tabella delle sezioni che contiene tutte le equazioni e le formule relative alle sezioni della trave (il momento di inerzia, area ecc…).
L'equazione per i vari centroidi è elencata di seguito:
| RIFERIMENTO | Cy (Distanza dal fondo) |
Cx (Distanza dal punto più a sinistra) |
Centroide di sezioni rettangolari o rettangolari |
||
|---|---|---|
 |
[matematica] \dfrac{h}{2} [matematica] |
[matematica] \dfrac{b}{2} [matematica] |
Centroide di una sezione rettangolare cava |
||
 |
[matematica] \dfrac{b}{2} [matematica] |
[matematica] \dfrac{h}{2} [matematica] |
Centroide di un cerchio o sezione circolare |
||
 |
[matematica] \dfrac{D}{2} [matematica] |
[matematica] \dfrac{D}{2} [matematica] |
Equazione del centroide di una sezione circolare cava |
||
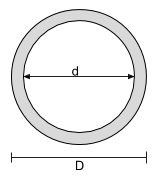 |
[matematica] \dfrac{D}{2} [matematica] |
[matematica] \dfrac{D}{2} [matematica] |
Centroide di un triangolo isoscele |
||
 |
[matematica] \dfrac{h}{3} [matematica] |
[matematica] \dfrac{b}{2} [matematica] |
Centroide di una trave a I |
||
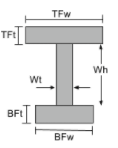 |
[matematica] \frac{TFw times TFt times left ( Bft + Wh + \frac{Tft}{2} \giusto )}{TFw volte TFt + Wt volte Wh + BFw times BFt} + [matematica] [matematica] \frac{Wt times Wh times left ( Bft + \frac{Wh}{2} \giusto )}{TFw volte TFt + Wt volte Wh + BFw times BFt} + [matematica] [matematica] \frac{BFw times BFt times left ( \frac{Bft}{2} \giusto )}{TFw volte TFt + Wt volte Wh + BFw times BFt} [matematica] |
[matematica] TFW > BFW, \frac{TFW}{2}[matematica] [matematica] BFW > TFW, \frac{BFW}{2} [matematica] |
Centroide di una sezione a T. |
||
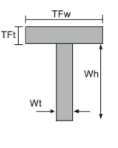 |
[matematica] \frac{Wt times Wh times left ( \frac{Wh}{2} \giusto )}{TFw volte TFt + Wt volte Wh } + [matematica] [matematica] \frac{TFw times TFt times left ( Wh + \frac{Tft}{2} \giusto ) }{TFw volte TFt + Wt volte Wh } [matematica] |
[matematica] \frac{TFW}{2} [matematica] |
Centroide di un cesareo |
||
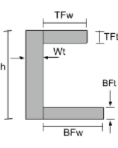 |
[matematica] \frac{TFw times TFt times left ( h – \frac{Tft}{2} \giusto )}{TFw volte TFt + Wt volte Wh + BFw times BFt} + [matematica] [matematica] \frac{Wt times h times left ( \frac{h}{2} \giusto )}{TFw volte TFt + Wt volte Wh + BFw times BFt} + [matematica] [matematica] \frac{BFw times BFt times left ( \frac{Bft}{2} \giusto )}{TFw volte TFt + Wt volte Wh + BFw times BFt} [matematica] |
[matematica] \frac{TFt times TFw times left ( wt + \frac{TFW}{2} \giusto )}{TFt times TFw + h volte Wt + BFt times BFw} + [matematica] [matematica] \frac{h times Wt times left ( \frac{wt}{2} \giusto )}{TFt times TFw + h volte Wt + BFt times BFw} + [matematica] [matematica] \frac{BFt times BFw times left ( wt + \frac{BFW}{2} \giusto )}{TFt times TFw + h volte Wt + BFt times BFw} [matematica] |
Centroide di un angolo |
||
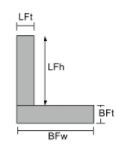 |
[matematica] \frac{LFt times LFh times left ( Bft + \frac{LFH}{2} \giusto ) }{LFt times LFh + BFw times BFt} + [matematica] [matematica] \frac{BFw times BFt times left ( \frac{Bft}{2} \giusto )}{LFt times LFh + BFw times BFt} [matematica] |
[matematica] \frac{LFh times LFt times left ( \frac{LFt}{2} \giusto )}{LFh times LFt + BFt times BFw} + [matematica] [matematica] \frac{BFt times BFw times left ( \frac{BFW}{2} \giusto )}{LFh times LFt + BFt times BFw} [matematica] |
Equazioni automatiche per il baricentro della trave
Dai un'occhiata al nostro Calcolatore del centroide gratuito, una versione semplificata di Il Generatore di Sezioni SkyCiv, per calcolare automaticamente il baricentro del raggio senza bisogno di calcoli manuali. Oppure registrati oggi per iniziare!


