Quando si esegue a Analisi dello spettro di risposta su una struttura, uno dei passaggi più importanti per ottenere i risultati desiderati è la definizione del metodo di combinazione modale che verrà utilizzato dal software per ottenere un unico risultato per lo spostamento, reazioni, forze interne, eccetera… per ogni grado di libertà dai risultati grezzi ottenuti per ogni modalità di vibrazione (risposte modali). Questi risultati combinati modali sono quelli utilizzati per progettare la struttura, ecco perché definire correttamente il metodo di combinazione modale è estremamente importante. In questo articolo, ci immergeremo in alcuni metodi di combinazione modale per l'analisi dello spettro di risposta.
È importante ricordare che uno dei passaggi più importanti durante un'analisi dello spettro di risposta è la valutazione della frequenza naturale per ciascuna modalità di vibrazione e il suo contributo di massa, controlla la nostra documentazione sull'analisi dinamica della frequenza.
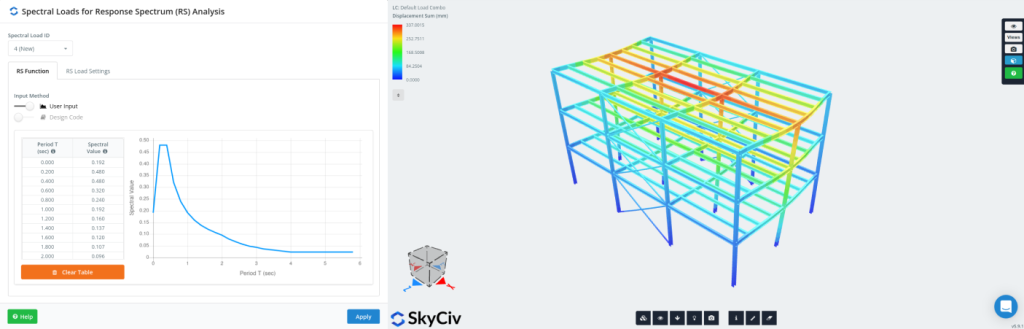
Metodi di combinazione modale per l'analisi dello spettro di risposta
Alcuni dei metodi più conosciuti e utilizzati per la combinazione modale sono:
- addominali: Somma assoluta
- SRSS: Radice quadrata della somma dei quadrati
- CQC: Combinazione quadratica completa
In generale, valori di picco della risposta totale (\(r_o\)) per spostamenti, forze interne, e le reazioni sono interessanti. Come menzionato prima, quel valore di picco è ottenuto combinando correttamente le risposte modali di picco (\(r_{n, Il}\))
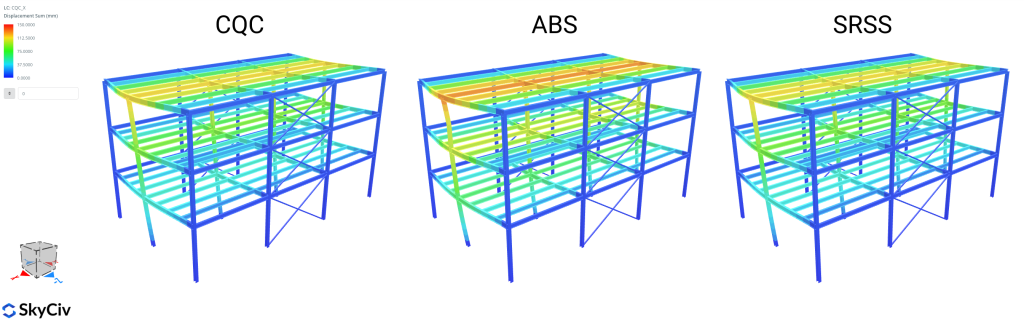
Somma assoluta (addominali)
Il metodo di combinazione modale Absolute Sum prende il valore assoluto del risultato (spostamento o forza interna) per ogni modalità di vibrazione e riassume tutti quei valori assoluti. Fisicamente, presuppone che tutte le risposte modali di picco si verifichino contemporaneamente. Facendo così, è il metodo più conservativo, in quanto rende positivo ogni contributo modale, e quindi, non è popolare nelle applicazioni di progettazione strutturale. La formula per calcolare il valore di picco della risposta totale è:
\(r_o=\sum_{n=1}^{N} |r_{n,Il}|\)
Dove,
\(n\) è il \(n^{ns}\) modo di vibrazione considerato nell'analisi
\(N\) è il numero totale di modi di vibrazione considerati nell'analisi
\(r_o\) è la risposta totale di picco
\(r_{n,Il}\) è la risposta modale di picco per \(n^{ns}\) modalità vibrazione
Radice quadrata della somma dei quadrati (SRSS)
Il metodo di combinazione modale della radice quadrata della somma dei quadrati prende la radice quadrata della somma dei quadrati del risultato per ciascuna modalità di vibrazione, fornendo una stima del picco della risposta totale. Questo metodo di combinazione modale fornisce eccellenti stime di risposta per strutture con frequenze naturali ben separate, per i casi in cui le frequenze naturali della struttura non sono ben separate questo metodo non dovrebbe essere utilizzato. Formalmente, la risposta totale di picco può essere espressa come segue:
\(r_o=\left(\somma_{n=1}^{N} r^{2}_{n,Il}\giusto)^{1/2}\)
Dove,
\(n\) è il \(n^{ns}\) modo di vibrazione considerato nell'analisi
\(N\) è il numero totale di modi di vibrazione considerati nell'analisi
\(r_o\) è la risposta totale di picco
\(r_{n,Il}\) è la risposta modale di picco per \(n^{ns}\) modalità vibrazione
Combinazione quadratica completa (CQC)
Il metodo della combinazione quadratica completa supera la limitazione menzionata per SRSS quando si combinano le risposte modali in una struttura con frequenze naturali ravvicinate. In questo metodo, la risposta totale di picco si ottiene applicando la seguente formula:
\(r_o=\left(\somma_{io=1}^{N}\somma_{n=1}^{N} \rho_{pollici} \cpunto r_{io} \cpunto r_{no} \giusto)^{1/2}\)
Dove,
\(n, \; i\) è il \(n^{ns}, \; io^{ns}\) modo di vibrazione considerato nell'analisi
\(N\) è il numero totale di modi di vibrazione considerati nell'analisi
\(r_o\) è la risposta totale di picco
\(r_{n,Il}, \; r_{io,Il}\) è la risposta modale di picco per \(n^{ns}, \; io^{ns}\) modalità vibrazione
\(\rho_{pollici}\) è il coefficiente di correlazione per le due modalità che vengono combinate ad ogni passo di sommatoria
La formula sopra può essere riscritta come due gruppi separati di sommatorie, il primo è identico al metodo di combinazione modale SRSS. La seconda sommatoria doppia comprende tutta la croce (\(i \neq n\)) condizioni, ognuno dei quali può essere positivo o negativo, questo produce il fatto che la stima per la risposta totale di picco utilizzando CQC potrebbe essere maggiore o minore della stima fornita da SRSS :
\(r_o=\left( \somma_{n=1}^{N} r^{2}_{n,Il} + \underbrace{\somma_{io=1}^{N}\somma_{n=1}^{N}}_{i \neq n} \rho_{pollici} \cpunto r_{io} \cpunto r_{no} \giusto)^{1/2}\)
Solo un termine nell'equazione per CQC non è stato definito: il coefficiente di correlazione. Una delle equazioni più utilizzate per questo coefficiente è:
\(\rho_{pollici} = frac{\xi^2(1+\Eurocodice di design con piastra di base in acciaio{pollici})^ 2}{(1-\Eurocodice di design con piastra di base in acciaio{pollici})^2+4\xi^2\beta_{pollici}}\)
Dove,
\(\Eurocodice di design con piastra di base in acciaio{pollici}\) è il rapporto tra le frequenze naturali del \(io^{ns}\) e \(n^{ns}\) modalità (\(\omega_i / \omega_n\))
\(\xi\) è il coefficiente di smorzamento della struttura
Riferimenti
Chopra, A. (2015, giugno 4). Dinamica delle strutture (4th ed.). Istruzione Superiore Pearson.
Novità in SkyCiv Structural 3D? Registrati oggi gratis!
Sviluppatore del prodotto
BEng (Civile)



