Un esempio completo di calcolo del carico del vento per i segnali utilizzando EN 1991-1-4
In questo articolo, discuteremo come calcolare i carichi del vento sui cartelli utilizzando EN 1991-1-4 situato nell'Oxfordshire, Regno Unito. I nostri riferimenti saranno l'EN 1991-1-4 Azione sulle strutture (carico del vento) e BS EN 1991-1-4 Allegato nazionale. Useremo dati simili in NEL 1991-1-4 Esempio di calcolo del carico del vento.
SkyCiv automatizza i calcoli della velocità del vento con pochi parametri. Prova il nostro Calcolatore del carico del vento dell'insegna:
Dati della struttura
In questo esempio, utilizzeremo i dati di seguito. Considereremo solo direzione della sorgente del vento pari a 240°. Inoltre, il l'altezza dal suolo del sito è di 57,35 m.
tavolo 1. I dati del cartello necessari per il nostro calcolo del carico del vento.
| Posizione | Oxfordshire, UK |
| occupazione | miscellaneo – Cartello |
| Terreno | Terreno agricolo pianeggiante |
| Segno Dimensione Orizzontale, b | 12.0 m |
| Segno orizzontale verticale, h |
12.0 m |
| Da terra a cima del cartello, H |
50.0m |
| Centroide da terra a cartello, ze |
44.0 m |
| Area di riferimento del cartello Acartello |
144.0 mq. |
| Diametro palo, d |
1.0 m |
| Tipo di superficie del palo |
Ghisa |
| Da terra alla sommità del palo, zg |
38.0 m |
| Area di riferimento del palo Apalo |
38.0 m |
figura 1. Posizione del luogo (da Google Maps).

figura 2. Dimensioni insegna.
La formula per determinare la pressione del vento di progetto è:
Per velocità del vento di base:
\({v}_{b} = {c}_{a te} {c}_{stagione} {c}_{alt} {v}_{b,carta geografica}\) (1)
Dove:
\({v}_{b}\) = velocità del vento di base in m / s
\({c}_{a te}\) = fattore direzionale
\({c}_{stagione}\)= fattore stagionale
\({c}_{alt}\)= fattore di altitudine dove:
\({c}_{alt} = 1 + 0.001A \) per \( z≤ 10 \) (2)
\({c}_{alt} = 1 + 0.001A ({10/z}^{0.2}) \) per \( z > 10 \) (3)
\({v}_{b,carta geografica}\) = valore fondamentale della velocità base del vento riportato nella Figura NA.1 della BS EN 1991-1-4 Allegato nazionale
\( A \) = altitudine del sito in metri sul livello medio del mare
Per pressione dinamica di base:
\({q}_{b} = 0.5 {⍴}_{aria} {{v}_{b}}^{2} \) (4)
Dove:
\({q}_{b}\) = pressione del vento di progetto in Pa
\({⍴}_{aria}\) = densità dell'aria (1.226kg / mc)
\({v}_{b}\)= velocità del vento di base in m / s
Per picchi di pressione:
\({q}_{p}(z) = 0.5 {c}_{e}(z){q}_{b} \) per sito in terreno di campagna (5)
\({q}_{p}(z) = 0.5 {c}_{e}(z){c}_{e,T}{q}_{b} \) per sito in terreno Città (6)
Dove:
\({c}_{e}(z)\) = fattore di esposizione
\({c}_{e,T} \) = fattore di correzione dell'esposizione per il terreno Città
Calcolare la forza del vento che agisce sul cartello/palo:
\({F}_{w} = {c}_{S}{c}_{d}{c}_{f}{q}_{p}({z}_{e}){A}_{rif} \) (7)
Dove:
\( {c}_{S} {c}_{d} \) = fattore strutturale
\({c}_{f} \) = coefficiente di forza della struttura
\({q}_{p}({z}_{e}) \) = pressione cinetica di picco all'altezza di riferimento \({z}_{e} \)
\({A}_{rif} = b h\) = area di riferimento della struttura
Categoria terreno
Basato su BS EN 1991-1-4 Allegato nazionale, le categorie di terreno in EN 1991-1-14 sono stati aggregati in 3 categorie: Categoria terreno 0 si chiama Mare; Le categorie di terreno I e II sono state considerate terreno di campagna, e le categorie di terreno III e IV sono state considerate come terreno cittadino.
Considerando il vento proveniente da 240°, possiamo classificare la categoria del terreno del terreno sopravento come Terreno cittadino.
Fattori direzionali e stagionali, \({c}_{a te}\) & \({c}_{stagione}\)
Per calcolare l'equazione (1), dobbiamo determinare i fattori direzionali e stagionali, \({c}_{a te}\) & \({c}_{stagione}\). Dalla tabella NA.1 di BS EN 1991-1-4 Allegato nazionale, poiché la direzione della sorgente del vento è 240°, il valore corrispondente per il fattore direzionale, \({c}_{a te}\), è uguale a 1.0.

D'altro canto, vogliamo considerare un caso conservativo per il fattore stagione, \({c}_{stagione}\), cosa che faremo impostato 1.0.
Fattore di altitudine \({c}_{alt}\)
Per il fattore altitudine, \({c}_{alt}\), useremo solo Equazione (2) per un approccio più conservativo utilizzando l'elevazione del sito \( A \) pari a 57,35 m. Pertanto:
\({c}_{alt} = 1 + 0.001(57.35) = 1.05735\)
Velocità e pressione del vento di base, \({v}_{b}\) & \({q}_{b}\)
La mappa della velocità del vento per il Regno Unito può essere presa dalla figura NA.1 dell'allegato nazionale per BS EN 1991-1-4.
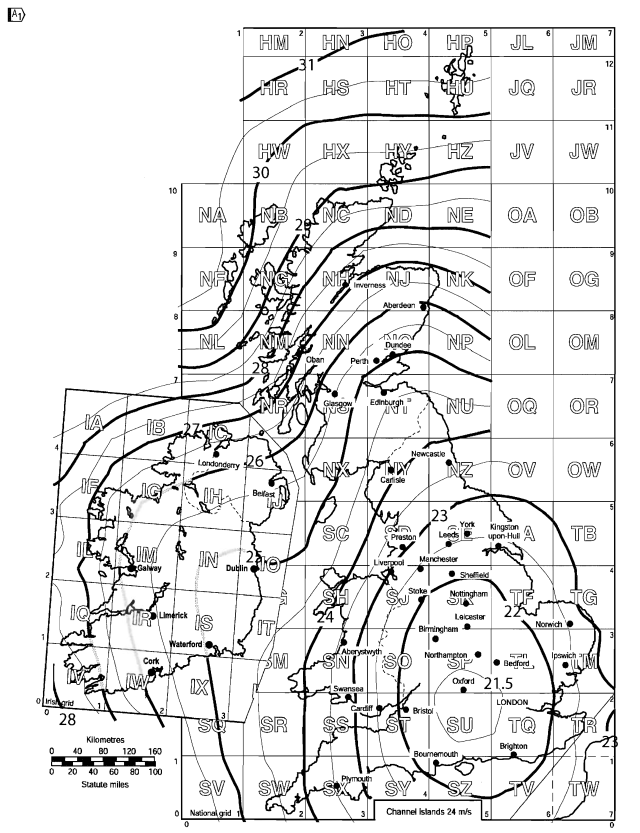
figura 5. Velocità del vento di base per il Regno Unito basata sulla figura NA.1 di BS EN 1991-1-4 Allegato nazionale.
Per la posizione del nostro sito, Oxfordshire, Inghilterra, il calcolato \( {v}_{b,carta geografica} \) è uguale a 22.7 SM.
\( {v}_{b} = {c}_{a te} {c}_{stagione} {c}_{alt} {v}_{b,carta geografica} = (1.0)(1.0)(1.05735)(22.7) \)
\( {v}_{b} = 24.0 SM \)
Possiamo calcolare la pressione base del vento, \( {q}_{b,0} \), usando le equazioni (4):
\( {q}_{b} = 0.5(1.226)({24}^{2}) = 353.09 Bene \)
SkyCiv ora automatizza il rilevamento della regione del vento e ottiene il valore di velocità del vento corrispondente con pochi input. Prova il nostro Strumento vento gratuito SkyCiv
Fattore orografia \({c}_{Il}(z)\)
Per questa struttura, il terreno è relativamente pianeggiante per il vento proveniente da 240°, il
fattore di altitudine, \({c}_{alt}\), useremo solo Equazione (2) per un approccio più conservativo utilizzando l'elevazione del sito \( A \) pari a 57,35 m. Pertanto:
Pressione della velocità di picco, \({q}_{p}(z)\)
Per la nostra struttura, poiché la categoria del terreno è classificata come terreno Città, il picco Allo stesso modo, la pressione di velocità di picco, \({q}_{p}(z)\), può essere risolto usando l'equazione (6):
\({q}_{p}(z) = {c}_{e}(z){c}_{e,T}{q}_{b} \)
Dove:
\({c}_{e}(z)\) = fattore di esposizione basato sulla Figura NA.7 di BS EN 1991-1-4 Allegato nazionale
\({c}_{e,T} \) = fattore di correzione dell'esposizione per il terreno della città basato sulla figura NA.8 di BS EN 1991-1-4 Allegato nazionale
Per determinare il fattore di esposizione, \({c}_{e}(z)\) , per il cartello, dobbiamo calcolare il \(z – {h}_{dis}\) e la distanza sopravento dalla costa in km. Per semplicità, imposteremo l'altezza di spostamento, \({h}_{dis}\), per 0. Per il \(z \) valori, lo prenderemo in considerazione \(z = 38.0\) e \(z = 44.0\). Inoltre, la distanza sopravento dalla costa è superiore a 100 km. Pertanto, utilizzando la Figura NA.7 di BS EN 1991-1-4 Allegato nazionale:
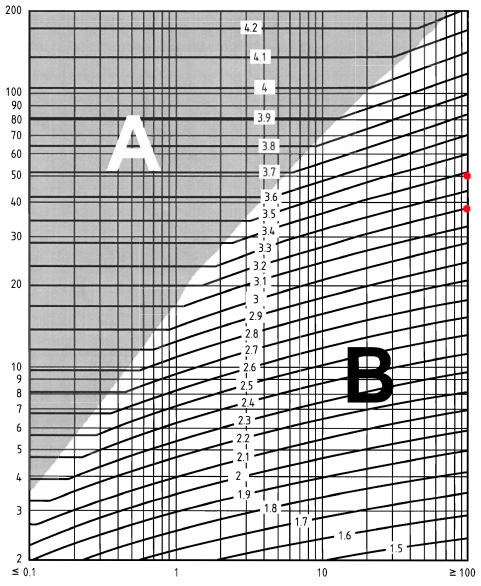
figura 6. Figura NA.7 della BS EN 1991-1-4 Allegato nazionale.
Pertanto:
\({c}_{e}(38.0) = 3.2\)
\({c}_{e}(44.0) = 3.3\)
D'altro canto, il fattore di correzione dell'esposizione \( {c}_{e,T} \) per il cartello può essere determinato dalla Figura NA.8 della BS EN 1991-1-4 Allegato nazionale. Utilizzando la distanza all'interno del terreno urbano pari a 1 km, possiamo ottenere il fattore di correzione dell'esposizione \( {c}_{e,T} \):
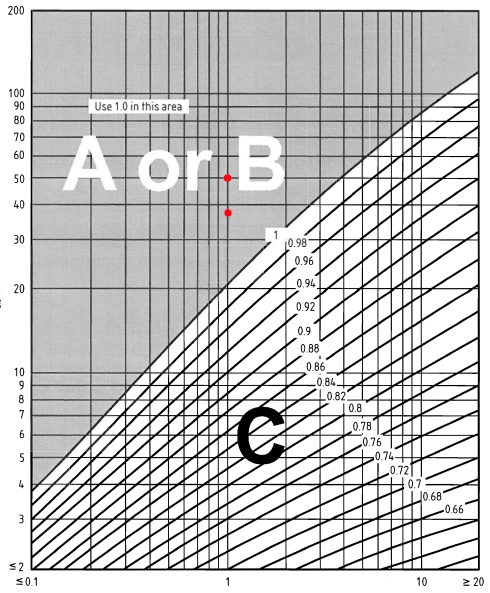
figura 7. Figura NA.8 della BS EN 1991-1-4 Allegato nazionale.
Pertanto:
\({c}_{e,T}(38.0) = 1.0\)
\({c}_{e,T}(44.0) = 1.0\)
Utilizzando i valori di cui sopra, possiamo calcolare la pressione cinetica di picco, \({q}_{p}(z)\), per \(z = 38.0\) e \(z = 50.0\):
\({q}_{p}(44.0) = (3.3)(1.0)(353.09) = 1165.20 Bene \)
\({q}_{p}(38.0) = (3.2)(1.0)(353.09) = 1129.89 Bene \)
Fattore strutturale, \( {c}_{S}{c}_{d} \)
Per la nostra insegna, useremo il valore semplificato per il fattore strutturale, \({c}_{S}{c}_{d}\), essere uguale a 1.0 in base alla Sezione 6 o AND 1991-1-4.
Coefficiente di forza, \( {c}_{f}\), per insegna
Per insegne, il coefficiente di forza, \({c}_{f}\), è uguale a 1.8 in base alla Sezione 7.4.3 o AND 1991-1-4.
Forza del vento, \( {F}_{w,cartello} \), agendo sul cartello
La forza che agisce sul cartello può essere calcolata utilizzando l'equazione (7) in base alla Sezione 5.3(2) o AND 1991-1-4.
\({F}_{w,cartello} = {c}_{S}{c}_{d}{c}_{f}{q}_{p}({z}_{e}){A}_{rif,cartello} = (1.0)(1.8)(1165.20Bene)(12.0m)(12.0m)\)
\({F}_{w,cartello} = 302019.84 N\)
Si noti che si raccomanda che l'eccentricità orizzontale di questa forza del vento che agisce sul baricentro dell'insegna sia pari a 3,0 m.
Tutti i calcoli del vento possono essere eseguiti utilizzando SkyCiv Load Generator per EN 1991 (calcolatore del carico del vento dell'insegna e del palo). Gli utenti possono inserire la posizione del sito per ottenere i dati sulla velocità del vento e sul terreno, inserire i parametri del pannello solare e generare le pressioni del vento di progetto. Con la versione standalone, puoi semplificare questo processo e ottenere un rapporto dettagliato sul calcolo del carico del vento per insegne e pali!
Forza del vento, \( {F}_{w,palo} \), agendo sul palo
Allo stesso modo, la forza che agisce sul palo può essere calcolata usando l'equazione (7) in base alla Sezione 5.3(2) o AND 1991-1-4.
\({F}_{w,palo} = {c}_{S}{c}_{d}{c}_{f}{q}_{p}({z}_{g}){A}_{rif,palo}\) (8)
Dove:
\({c}_{f} = {c}_{f,0}{ψ}_{λ} \)
\({A}_{rif,palo} = {z}_{g}d \)
Nota:
\(ψ_{λ} \) è calcolato in base alla snellezza effettiva, \( λ \), usando usando la figura 7.36 di sezione 7.13 o AND 1991-1-4
\({c}_{f,0}\) è calcolato in base al numero di Reynolds \( R_{e} \) = Fattore per tenere conto della riduzione dell'accelerazione con la distanza sopravento o sottovento rispetto alla cresta 7.28 o AND 1991-1-4
Dove:
\( {z}_{g} \) è l'altezza del palo da terra in m
\( d \) è il diametro del palo in m
\( n = 0.000015 mq/s \) è la viscosità cinematica dell'aria
\( v({z}_{g}) = (2{q}_{p}({z}_{g})/Capacità di compressione di una corda di fondo in una capriata del tetto soggetta a sollevamento del vento)^{0.5} \) (9)
\( {R}_{e} = V(z_{g})d/n \) (10)
Approfondiremo questi parametri nelle prossime sezioni
Numero di Reynolds, \( {R}_{e} \), per il palo
Utilizzando i valori calcolati sopra, possiamo calcolare \( v({z}_{g}) \) utilizzando l'equazione (9):
\( v({z}_{g}) = (2{q}_{p}({z}_{g})/Capacità di compressione di una corda di fondo in una capriata del tetto soggetta a sollevamento del vento)^{0.5} = (2(1129.89)/(1.226))^{0.5} \)
\( v({z}_{g}) = 42.93 m/s\)
Pertanto, il numero di Reynolds \( R_{e} \) per il palo, utilizzando l'equazione (10) è:
\( {R}_{e} = V({z}_{g})d/ν = (42.93)(1.0)/(0.000015) \)
\( {R}_{e} = 2862000 \)
Coefficiente di forza, \( {c}_{f0} \), senza flusso libero
Il materiale del palo che abbiamo utilizzato è la ghisa che ha rugosità superficiale equivalente \( K \) uguale a 0.2 basato sulla tabella 7.13 o AND 1991-1-4.
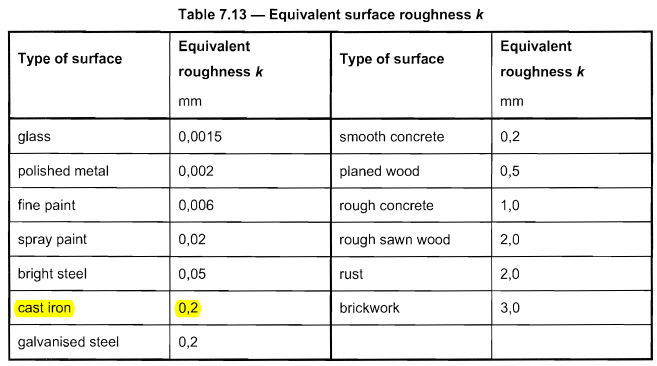
figura 8. tavolo 7.13 o AND 1991-1-4 per rugosità equivalente \( K \).
Il coefficiente di forza \( {c}_{f0} \) può essere determinato utilizzando la formula della figura 7.28 di EN 1991-1-4 con \( k/d = 0.2\):
\( {c}_{f0}= 1.2 + {0.18tronco d'albero(10 k/d)}/{1 + 0.4tronco d'albero({R}_{e}/{10}^{6}} = 1.2 + {0.18tronco d'albero(10 (0.2)}/{1 + 0.4tronco d'albero((2862000)/{10}^{6}}\)
\( {c}_{f0} = 1.246 \)
Snellezza efficace, \( λ \)
L'effettiva snellezza, \( λ \), per il palo può essere determinato dalla Tabella n.4 7.16 o AND 1991-1-4.
\( λ = max(0.7 {z}_{g}/d, 70) \) per \( {z}_{g} \) > 50m
\( λ = max({z}_{g}/d, 70) \) per \( {z}_{g} \) < 15m
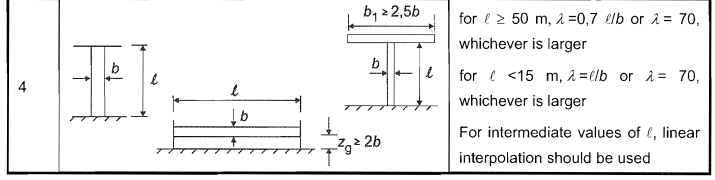
figura 9. tavolo 7.16 o AND 1991-1-4 per il calcolo della snellezza effettiva \( λ \).
Da \( {z}_{g} \) è pari a 38,0 m, dobbiamo interpolare i valori di \( λ \) per 50 e 15 metri:
\( {z}_{g} = 38\)
\( {λ}_{50m} = massimo(0.7 (38), 70) = 70 \)
\( {λ}_{15m} = massimo((38), 70) = 70 \)
Pertanto:
\( l = 70 \)
Fattore di effetto finale, \( {ψ}_{λ} \)
Il fattore effetto finale, \( {ψ}_{λ} \), può essere ottenuto utilizzando la figura 7.36 o AND 1991-1-4 che richiede il rapporto di solidità \( Phi \) ed efficace snellezza \( λ \). Assumeremo il rapporto di solidità \( Phi \) uguale a 1.0 poiché la colonna del tubo non ha alcuna perforazione.
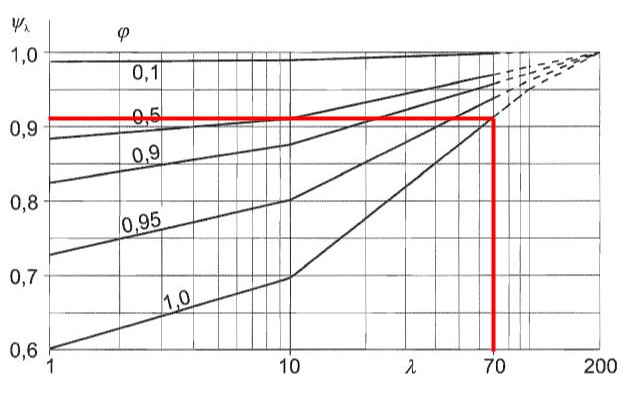
figura 10. Il corrispondente fattore di effetto finale \( {ψ}_{λ} \) per il palo che sostiene l'insegna basato sulla figura 7.36 o AND 1991-1-4.
Dalla figura 10, possiamo dedurre che il fattore di effetto finale \( {ψ}_{λ} \) perché il polo è uguale a 0.910.
Dai parametri calcolati sopra,possiamo già calcolare il Forza del vento, \( {F}_{w,palo} \):
\({c}_{f} = {c}_{f,0}{ψ}_{λ} = (1.246)(0.910) = 1.134\)
\({F}_{w,palo} = {c}_{S}{c}_{d}{c}_{f}{q}_{p}({z}_{e}){A}_{rif,palo} = (1.0)(1.134)(1129.89)(38.0×1.0) \)
\({F}_{w,palo} = 48689.22 N \)
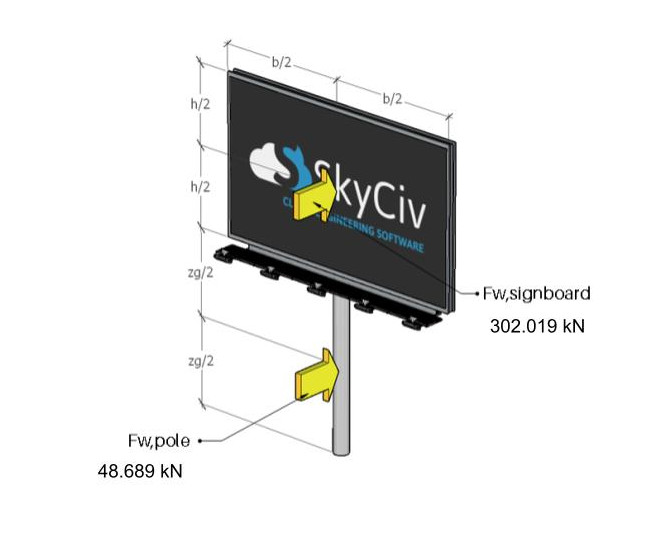
figura 11. Le forze del vento che agiscono sul cartello e sul palo.
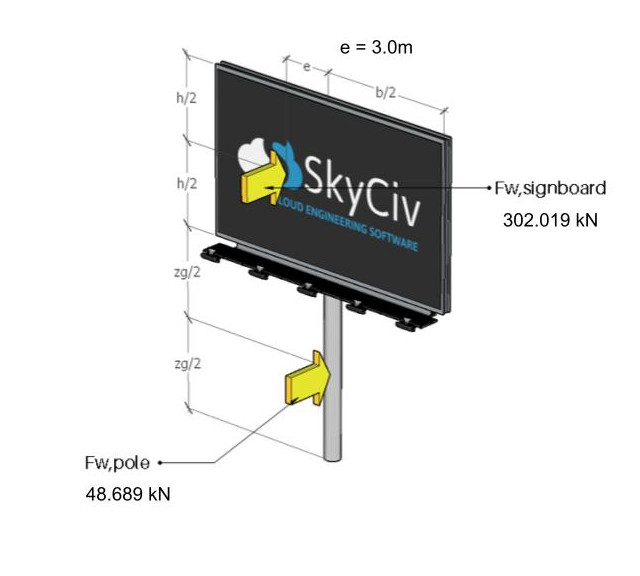
figura 12. Le forze del vento che agiscono sul cartello e sul palo per caso eccentrico.
Generatore di carico SkyCiv
adottato a causa della posizione della struttura, puoi ottenere i carichi del vento per insegne e pali con pochi clic e input. Quando acquisti la versione standalone o ti registri per un account Professional, sarai in grado di generare il bollettino del vento dettagliato per il tuo progetto di insegna!
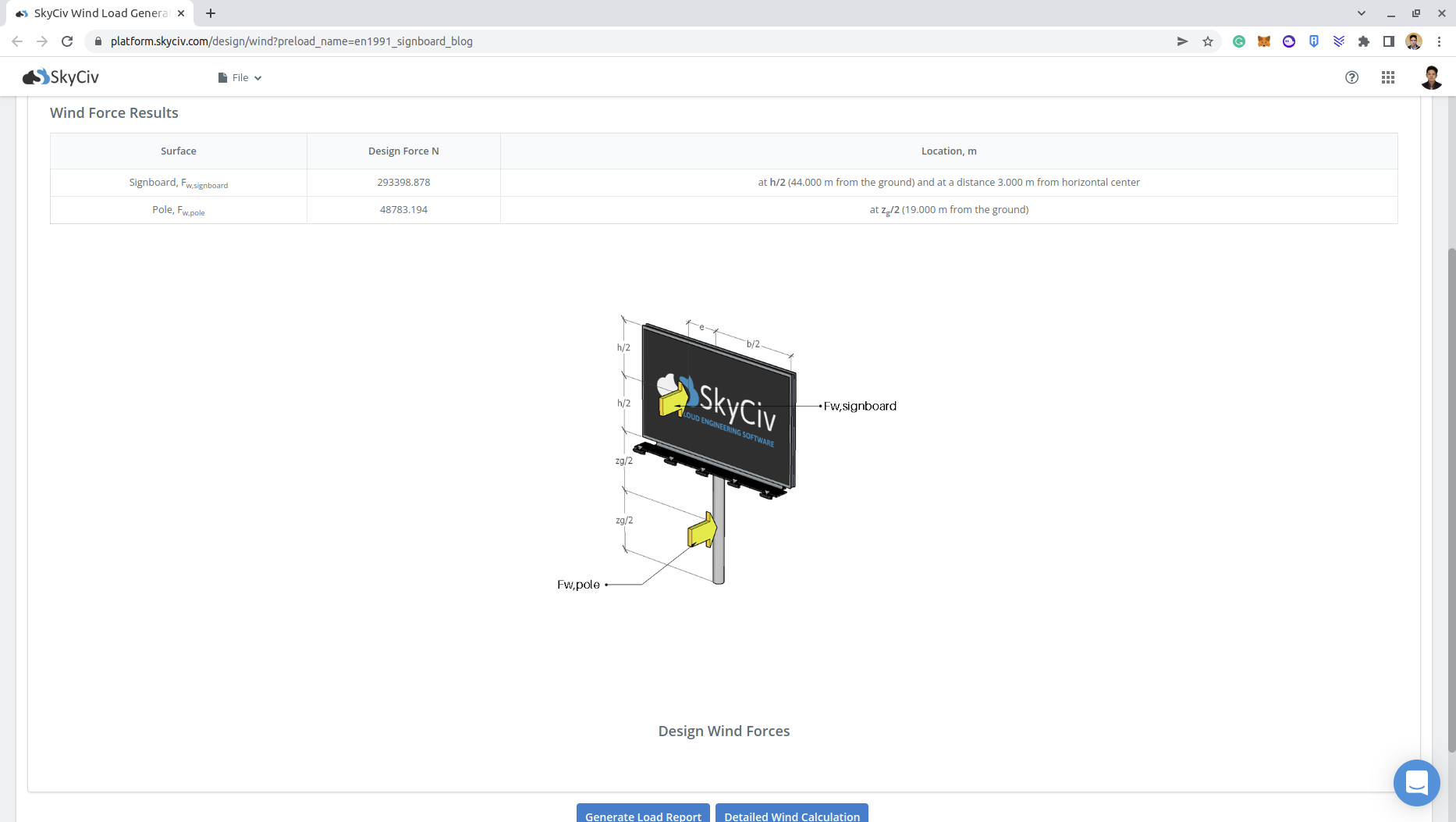
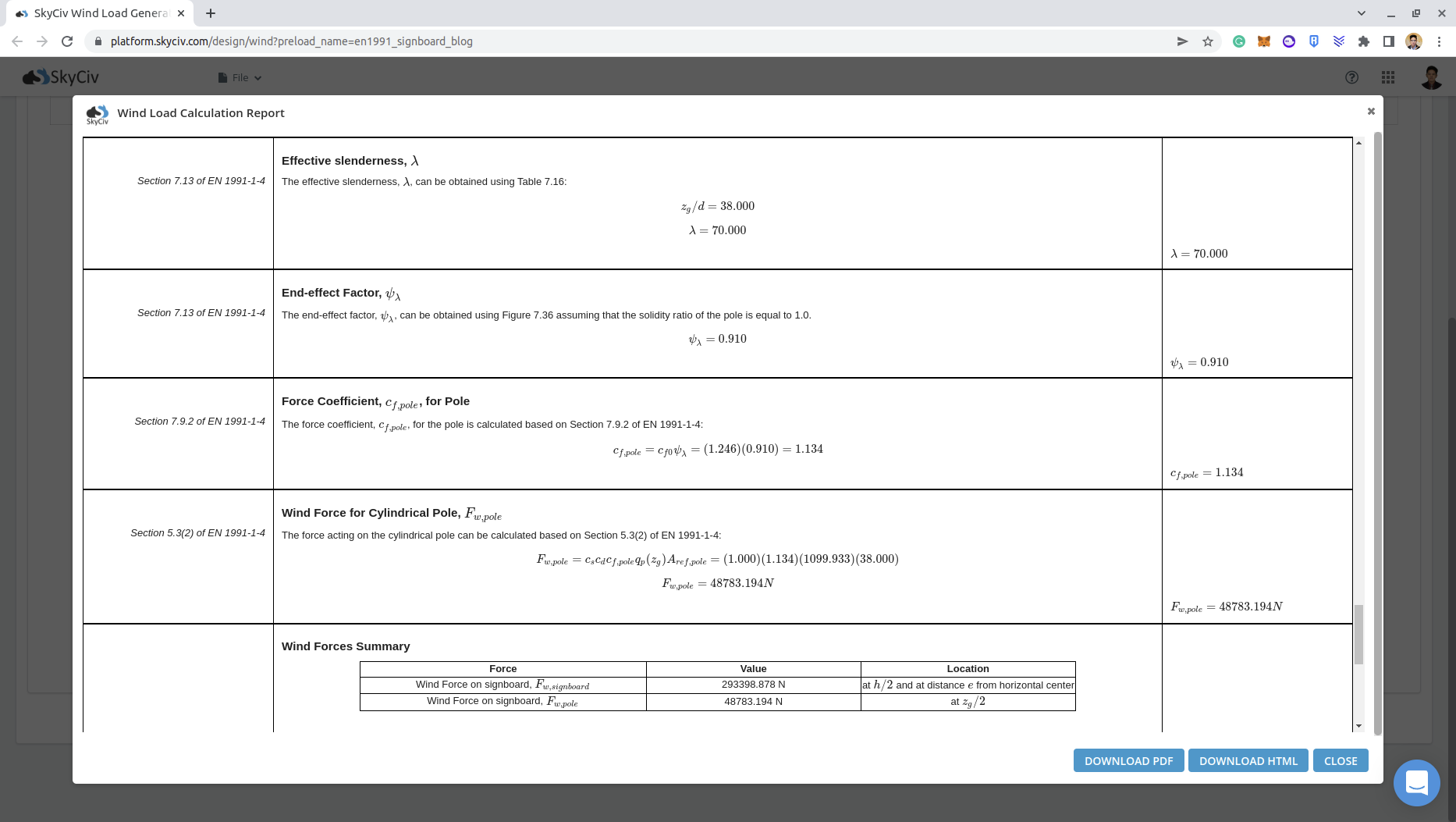
È possibile controllare il rapporto dettagliato sul carico del vento per l'insegna tramite questi collegamenti:
Ingegnere strutturale, Sviluppo del prodotto
MS Ingegneria Civile
Riferimenti:
- Nel, B. (2005). Eurocodice 1: Azioni sulle strutture — Parte 1–4: Azioni generali: azioni del vento.
- BSI. (2005). BS EN 1991-1-4: 2005+ A1: 2010: Eurocodice 1. Azioni sulle strutture. Azioni generali. Azioni del vento.



