Η ροπή αδράνειας είναι μια σημαντική γεωμετρική ιδιότητα που χρησιμοποιείται στη δομική μηχανική. Σχετίζεται άμεσα με την αντοχή του υλικού που έχει το τμήμα σας. Γενικά, υψηλότερη ροπή αδράνειας συνεπάγεται μεγαλύτερη αντοχή στο τμήμα, με αποτέλεσμα μειωμένη παραμόρφωση όταν υποβάλλεται σε φορτίο. Ο χαρακτηρισμός “στιγμή αδράνειας” είναι πραγματικά μια ευρέως χρησιμοποιούμενη εσφαλμένη ονομασία, καθώς αυτή η ιδιότητα δεν έχει καμία σχέση με την αδράνεια. Η σωστή τεχνική ονομασία είναι στην πραγματικότητα Δεύτερη στιγμή της περιοχής. Αυτός ο χαρακτηρισμός περιγράφει με μεγαλύτερη ακρίβεια τι μετράται αυτή η ιδιότητα, το οποίο μπορεί να είναι περίπου ως μέτρο του πόσο μακριά είναι η περιοχή του τμήματος από τον ουδέτερο άξονα.

Πίνακας περιεχομένων

• Ροπή αδράνειας τύπου ορθογωνίου
• Ορθογώνιες κοίλες τομές (RHS)

Ροπή αδράνειας τύπου ορθογωνίου

Ο γενικός τύπος που χρησιμοποιείται για τον προσδιορισμό της ροπής αδράνειας ενός ορθογωνίου είναι:

[μαθηματικά] ΕΓΩ_{xx}[object Window]{BD^3}{12} , ΕΓΩ_{εε}[object Window]{B^3D}{12} [μαθηματικά]

Όπου το xx και εε αναφέρονται στον συγκεκριμένο άξονα, ή κατεύθυνση, εξετάζεται.

Είναι μια κοινή σύμβαση δομικής μηχανικής που σι αναφέρεται στο πλάτος του ορθογωνίου, παράλληλα με ένα συμβατικά οριζόντιος άξονας x.

Ομοίως, ρε αναφέρεται στο βάθος του ορθογωνίου, παράλληλα με ένα συμβατικά κατακόρυφος άξονας y.

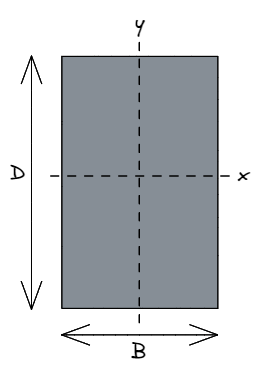
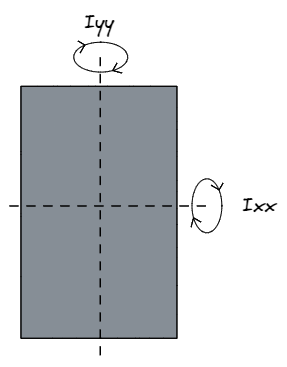
Όταν οι δομικοί μηχανικοί αναφέρονται Ιχχ αναφέρονται στην αντοχή ενός τμήματος σχετικά με ο άξονας x, που σημαίνει σε κατεύθυνση παράλληλη προς το ρε διάσταση, ή άξονα y. Ομοίως, Εεεε αναφέρεται στη δύναμη σχετικά με ο άξονας y, που σημαίνει σε κατεύθυνση παράλληλη προς το σι διάσταση, ή άξονα x.

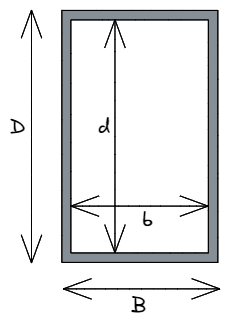
Ορθογώνιες κοίλες τομές (RHS)

Ενώ οι μηχανικοί θα μπορούσαν υποθετικά να χρησιμοποιήσουν συμπαγή ορθογώνια τμήματα κατά το σχεδιασμό, αυτό θα χρησιμοποιούσε σημαντικά μεγαλύτερη ποσότητα πρώτης ύλης, με αντίστοιχες αυξήσεις σε βάρος και κόστος. Είναι πολύ πιο συνηθισμένο να χρησιμοποιείται ορθογώνιο κοίλα τμήματα (που συνήθως αναφέρεται ως an RHS). Εδώ μπορούμε να χρησιμοποιήσουμε την ίδια εξίσωση που ορίστηκε παραπάνω για τη γενική ορθογώνια περίπτωση, ωστόσο, πρέπει να αφαιρέσουμε το εσωτερικό κοίλος περιοχή του ορθογωνίου:

[μαθηματικά] ΕΓΩ_{xx}[object Window]{BD^3}{12} – \dfrac{bd^3}{12} [μαθηματικά]

Σε αυτή την περίπτωση, πεζά σι και ρε δηλώνουμε το μέγεθος της κοίλης περιοχής μέσα στο ορθογώνιο που πρέπει να αφαιρέσουμε από τις εξωτερικές διαστάσεις του σχήματος, είναι κεφαλαίο σι και ρε. Η διαφορά μεταξύ κάθε αντίστοιχης διάστασης αναφέρεται στο πάχος του υλικού σε αυτή τη διάσταση – δηλ. σι – b = συνολικό πάχος του υλικού παράλληλο στον άξονα x.

Εκτός από τα ξεκάθαρα παραδείγματα χρήσης βάρους και υλικού, γιατί οι κοίλες τομές συχνά περιγράφονται ως περισσότερες αποτελεσματικός από τους συμπαγείς ομολόγους τους?

Θεωρήστε μια δοκό που υφίσταται κατακόρυφο φορτίο προς τα κάτω. Αναμένουμε ότι οι κορυφαίες ίνες του υλικού θα υποστούν θλιπτική δύναμη, ενώ οι αντίστοιχες ίνες πυθμένα θα υποστούν δύναμη εφελκυσμού. Οι ίνες κατά μήκος του ουδέτερου άξονα του τμήματος (παράλληλα με το κέντρο του τμήματος) ωστόσο, δεν θα βιώσουν ούτε συμπίεση ούτε τάση, εξ ου και το όνομα ουδέτερος άξονας.

Σημαντικό, ο μέγεθος από αυτές τις θλιπτικές ή εφελκυστικές δυνάμεις εξαρτώνται από την απόσταση από αυτόν τον ουδέτερο άξονα – υλικό πιο κοντά στον ουδέτερο άξονα χρειάζεται να αντισταθεί το κάτω μέρος του τμήματος έχει σημειακές ράβδους δύναμη.

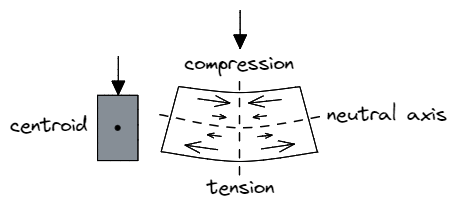
Σαν άποτέλεσμα, το εσωτερικό υλικό ενός συμπαγούς τμήματος αντιστέκεται σε μικρή μόνο δύναμη ενώ καταλαμβάνει μεγάλη επιφάνεια, αφού το πιο εξωτερικό υλικό φέρει το μεγαλύτερο φορτίο! Η αφαίρεση αυτού του εσωτερικού τμήματος του τμήματος και η κούφισή του βελτιώνει κατά συνέπεια το αποδοτικότητα του τμήματος ως προς το βάρος του, κόστος, και χρήση υλικών.

συμπέρασμα

Συνοψίζοντας, ο τύπος για τον προσδιορισμό της ροπής αδράνειας ενός ορθογωνίου είναι Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. Για ορθογώνια κοίλα τμήματα, ο τύπος είναι Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.

Η αδράνεια ροπής είναι σημαντική τόσο για τη δύναμη/τάση της ροπής κάμψης όσο και για την παραμόρφωση. Αυτό φαίνεται στους τύπους τους, όπως και στις δύο περιπτώσεις, Εγώ (Στιγμή αδράνειας) Λεπτομερής ανάλυση:

Πηγή: Ροπή αδράνειας τύπου Κύκλου

Πηγή: Ροπή αδράνειας τύπου Κύκλου

Ροπή Αδράνειας Υπολογιστής Κύκλου

Αν θέλετε να μάθετε περισσότερα, ρίξτε μια ματιά στο σεμινάριο μας για το Ροπή Αδράνειας Κύκλου για να δείτε πώς συγκρίνονται τα σχήματα κυκλικής και ορθογώνιας τομής.

Υπολογιστής δωρεάν ροπής αδράνειας