Πίνακας περιεχομένων

• Τύποι στηρίξεων και οι αντιδράσεις τους
• Ένας βήμα προς βήμα οδηγός για τον προσδιορισμό των αντιδράσεων υποστήριξης σε δοκούς
  • Άθροισμα Στιγμών (ΣΜ = 0)
  • Άθροισμα οριζόντιων δυνάμεων (ΣFy = 0)
• Λογισμικό SkyCiv Beam

Τύποι στηρίξεων και οι αντιδράσεις τους

Σε αυτό το άρθρο, συζητάμε τον τύπο της δύναμης αντίδρασης και τον τρόπο εύρεσης των αντιδράσεων υποστήριξης. Πρώτα, Είναι σημαντικό επίσης να κατανοήσετε τους διαφορετικούς τύπους στηρίξεων και τις αντιδράσεις που παράγουν στο μοντέλο ανάλυσής σας, συμπεριλαμβανομένων των στιγμών αντίδρασης. Παρακάτω είναι ένα σύντομο φύλλο εξαπάτησης των διαφορετικών τύπων υποστήριξης και των αντιδράσεών τους:

Τύπος Υποστήριξης	Μετάφραση	Περιστροφή	Σημειώσεις
Διορθώθηκε η υποστήριξη	Διορθώθηκε προς όλες τις κατευθύνσεις Αντιδράσεις στο Χ,ΚΑΙ,ΜΕ	Διορθώθηκε προς όλες τις κατευθύνσεις Αντιδράσεις στο Χ,ΚΑΙ,ΜΕ	FFFFFF – Αντιδράσεις σε όλους τους βαθμούς ελευθερίας
Οριζόντια υποστήριξη κυλίνδρων	Διορθώθηκε στο Υ Αντιδράσεις μόνο προς την κατεύθυνση Υ	Κυκλοφόρησε σε όλες τις κατευθύνσεις Χωρίς περιστροφικές αντιδράσεις	RFFRRR – Οι αντιδράσεις είναι μόνο προς την κατεύθυνση Υ
Καρφιτσωμένη ή αρθρωτή υποστήριξη	Διορθώθηκε στο Χ,ΚΑΙ,ΜΕ Αντιδράσεις στο Χ,ΚΑΙ,ΜΕ	Κυκλοφόρησε σε όλες τις κατευθύνσεις Χωρίς περιστροφικές αντιδράσεις	FFFRRR – Αντιδράσεις σε όλη τη μετάφραση, καμία εκ περιτροπής
Υποστήριξη Cantilever	Διορθώθηκε προς όλες τις κατευθύνσεις Αντιδράσεις στο Χ,ΚΑΙ,ΜΕ	Διορθώθηκε προς όλες τις κατευθύνσεις Αντιδράσεις στο Χ,ΚΑΙ,ΜΕ	Το ίδιο με το σταθερό

Ένας βήμα προς βήμα οδηγός για τον προσδιορισμό των αντιδράσεων υποστήριξης σε δοκούς:

Ο προσδιορισμός των αντιδράσεων στα στηρίγματα είναι πάντα το πρώτο βήμα στην ανάλυση μιας δομής δοκού, και είναι γενικά το πιο εύκολο. Περιλαμβάνει τον υπολογισμό τόσο του τύπου της δύναμης αντίδρασης όσο και των ροπών αντίδρασης στα στηρίγματα (υποστηρίζει Α και Β στο παρακάτω παράδειγμα) λόγω των δυνάμεων που δρουν στη δέσμη. Ο τύπος της δύναμης αντίδρασης χρησιμοποιείται για την εύρεση των δυνάμεων που ασκούνται στα στηρίγματα λόγω των φορτίων που ασκούνται στη δοκό. Εξάλλου, Είναι σημαντικό να κατανοήσουμε τις στιγμές αντίδρασης σε σταθερά στηρίγματα για την επίλυση του προβλήματος. Θα πρέπει να το γνωρίζετε αυτό για να προχωρήσετε και να υπολογίσετε διαγράμματα ροπών κάμψης (BMD) και διαγράμματα δύναμης διάτμησης (SFD); ένα σημαντικό μέρος των στατικών σας και των δομικών μαθημάτων κολλεγίων / πανεπιστημίων. Το SkyCiv προσφέρει ένα ισχυρό Δωρεάν Υπολογιστής Αντίδρασης που σας επιτρέπει να μοντελοποιήσετε οποιαδήποτε δέσμη και να δείξετε αυτούς τους υπολογισμούς χεριών για εσάς, αλλά είναι επίσης μια σημαντική έννοια που πρέπει να κατανοήσουμε.

Εκμάθηση βίντεο: Προσδιορίστε τις αντιδράσεις στα στηρίγματα

Ακολουθήστε μας στο YouTube

Κατά την επίλυση ενός τέτοιου προβλήματος θέλουμε πρώτα να θυμόμαστε ότι η δέσμη είναι στατική; που σημαίνει ότι δεν κινείται. Από την απλή φυσική, Αυτό σημαίνει ότι το άθροισμα των δυνάμεων στην κατεύθυνση y ισούται με μηδέν (δηλ. οι συνολικές καθοδικές δυνάμεις ισούνται με τις συνολικές ανοδικές δυνάμεις). Ένας δεύτερος τύπος που πρέπει να θυμάστε είναι ότι το άθροισμα των στιγμών για οποιοδήποτε δεδομένο σημείο είναι μηδέν. Αυτό συμβαίνει επειδή η δέσμη είναι στατική και συνεπώς δεν περιστρέφεται.

Για τον προσδιορισμό των αντιδράσεων στα στηρίγματα, ακολουθήστε αυτά τα απλά βήματα:

1. Άθροισμα Στιγμών (ΣΜ = 0)

Το μόνο που πρέπει να γνωρίζουμε για στιγμές σε αυτό το στάδιο είναι ότι είναι ίσες με τη δύναμη που πολλαπλασιάζεται με την απόσταση από ένα σημείο (δηλ. η δύναμη x απόσταση από ένα σημείο). Εξετάστε ένα απλό παράδειγμα δέσμης 4 μέτρων με στήριγμα ακίδων στο Α και στήριγμα κυλίνδρου στο Β. Το διάγραμμα ελεύθερου σώματος φαίνεται παρακάτω όπου το Α_και και Β_και είναι οι κάθετες αντιδράσεις στα στηρίγματα: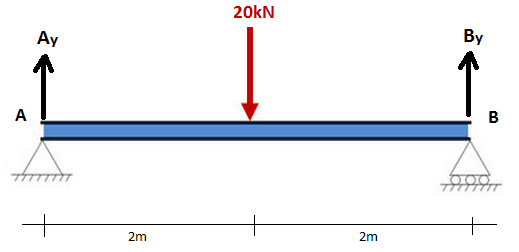

Θέλουμε πρώτα να εξετάσουμε το άθροισμα των ροπών για το σημείο Β και να το αφήσουμε ίσο με μηδέν. Επιλέξαμε το σημείο Β για να αποδείξουμε ότι αυτό μπορεί να γίνει και στα δύο άκρα της δοκού (υπό την προϋπόθεση ότι υποστηρίζεται από pin). Ωστόσο, θα μπορούσατε εξίσου εύκολα να εργαστείτε από το σημείο Α. Έτσι, τώρα αθροίζουμε τις στιγμές για το σημείο Β και αφήνουμε το άθροισμα ίσο 0:

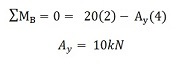
ΣΗΜΕΙΩΣΗ: Η σύμβαση σημείου που επιλέξαμε είναι ότι οι αντίστροφης ροπής στιγμές είναι θετικές και οι δεξιόστροφες στιγμές είναι αρνητικές. Αυτή είναι η πιο κοινή σύμβαση σημαδιών, αλλά εξαρτάται από εσάς. Πρέπει να χρησιμοποιείτε ΠΑΝΤΑ την ίδια σύμβαση σημαδιών σε όλο το πρόβλημα. Χρησιμοποιείτε πάντα την ίδια σύμβαση σημαδιών από την αρχή. Έχουμε τώρα την πρώτη μας εξίσωση. Πρέπει να λύσουμε μια άλλη εξίσωση για να βρούμε το Β_και (η κατακόρυφη δύναμη αντίδρασης στο υποστήριγμα Β).

2. Άθροισμα οριζόντιων δυνάμεων (ΣΦ_και = 0)

Αθροίστε τις δυνάμεις στο y (κατακόρυφος) κατεύθυνση και αφήστε το άθροισμα ίσο με μηδέν. Θυμηθείτε να συμπεριλάβετε όλες τις δυνάμεις, συμπεριλαμβανομένων των αντιδράσεων και των κανονικών φορτίων, όπως τα σημειακά φορτία. Αν λοιπόν αθροίσουμε τις δυνάμεις στην κατεύθυνση y για το παραπάνω παράδειγμα, έχουμε την ακόλουθη εξίσωση:

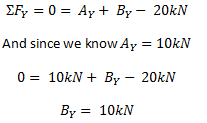
ΣΗΜΕΙΩΣΗ: Και πάλι κολλήσαμε σε μια σύμβαση σηματοδότησης που επρόκειτο να αναλάβει ανοδικές δυνάμεις (οι αντιδράσεις μας) ως θετικές και καθοδικές δυνάμεις (το σημειακό φορτίο) ως αρνητικό. Θυμηθείτε ότι η σύμβαση υπογραφής εξαρτάται από εσάς, αλλά πρέπει ΠΑΝΤΑ να χρησιμοποιείτε την ίδια σύμβαση σημαδιών σε όλο το πρόβλημα.

Οπότε το έχουμε, χρησιμοποιήσαμε τις δύο παραπάνω εξισώσεις (άθροισμα ροπών ισούται με μηδέν και άθροισμα κατακόρυφων δυνάμεων ισούται με μηδέν) και υπολόγισε ότι η αντίδραση στο υποστήριγμα Α είναι 10 kN και η αντίδραση στο υποστήριγμα B 10kN. Αυτό έχει νόημα καθώς το σημειακό φορτίο είναι ακριβώς στη μέση της δέσμης, που σημαίνει ότι και τα δύο στηρίγματα πρέπει να έχουν τις ίδιες κατακόρυφες δυνάμεις (δηλ. είναι συμμετρικό).

Κατά τον υπολογισμό των αντιδράσεων υποστήριξης, χρησιμοποιείται τόσο το άθροισμα των δυνάμεων όσο και το άθροισμα των ροπών. Ο τύπος της δύναμης αντίδρασης βοηθά στον υπολογισμό των κατακόρυφων και οριζόντιων δυνάμεων, ενώ η άθροιση των ροπών αντίδρασης σάς επιτρέπει να διασφαλίσετε ότι η δέσμη παραμένει σε στατική ισορροπία.

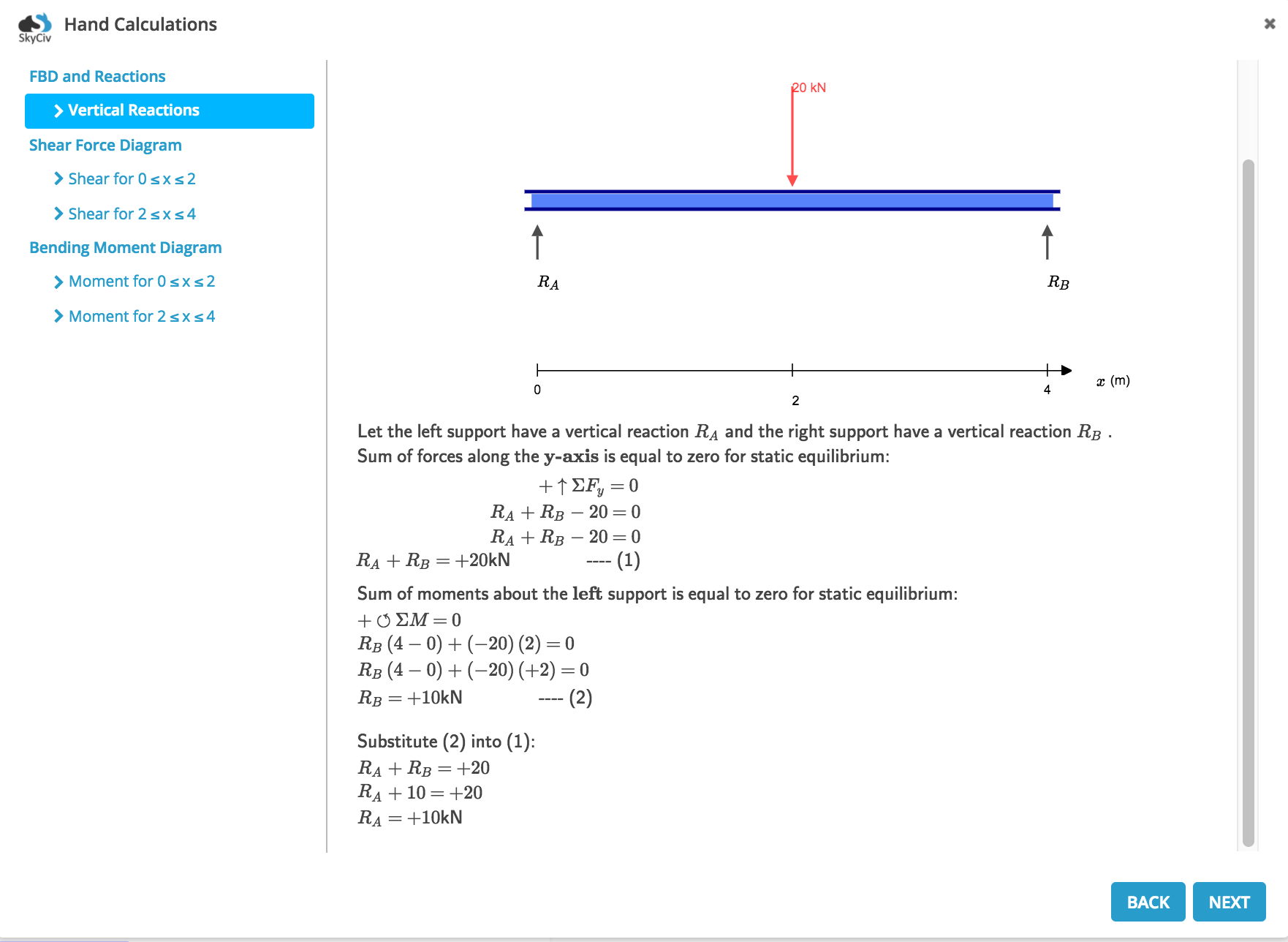
Συνοψίζοντας, εδώ είναι το πλήρες υπολογισμοί χεριών παράγεται από SkyCiv Beam:

Λογισμικό SkyCiv Beam

Μέσα από αυτό το άρθρο, Έχετε μάθει την έννοια των δυνάμεων αντίδρασης στα στηρίγματα και πώς να υπολογίζετε τις αντιδράσεις υποστήριξης. Λογισμικό ανάλυσης δέσμης SkyCiv επιτρέπει στους χρήστες να αναλύουν τις δομές δοκών εύκολα και με ακρίβεια. Μπορείτε να λάβετε μια ανάλυση του μέλους δοκού σας, συμπεριλαμβανομένων των αντιδράσεων, δύναμη διάτμησης, στιγμή κάμψης, εκτροπή, στρες, και απροσδιόριστα δοκάρια μέσα σε λίγα δευτερόλεπτα.

Αν θέλετε να το δοκιμάσετε πρώτα, Υπολογιστής δωρεάν δέσμης είναι ένας πολύ καλός τρόπος για να ξεκινήσετε, ή απλά εγγραφείτε δωρεάν σήμερα!