Λεπτομέρειες μοντέλου και παράμετροι
Προσδιορίστε τις μετατοπίσεις ενός ημισφαιρικού κελύφους που υπόκεινται σε συμπυκνωμένα εφελκυστικά και συμπιεστικά φορτία σε δύο ορθογώνιες ακτινικές κατευθύνσεις.
Μόνο ένα τέταρτο μοντέλο μπορεί να αναλυθεί λόγω συμμετρίας.
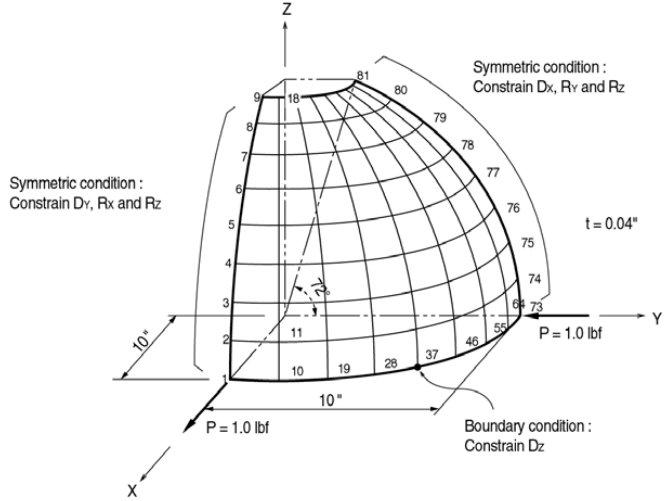
Δομική γεωμετρία
- Τύπος ανάλυσης
3-D στατική ανάλυση - Διάσταση
Ακτίνα κύκλου: 10.0 σε - Τύπος πλάκας
Στρες Mindlin Plane - Υλικό
Δομικού χάλυβα
Το μέτρο του Young: 68250 ksi
Αναλογία Poisson: 0.3 - Στοιχείο ιδιοκτησίας
Πάχος πλάκας: 0.04 σε - Υποστήριξη ορίων
Κόμβοι 1 – 9: Περιορίστε Dy, Rx και Rz. (Συμμετρική για το επίπεδο X-Z)
Κόμβοι 73 – 81: Περιορισμός Dx, Ry και Rz. (Συμμετρική για το επίπεδο Υ-Ζ)
Κόμβος 37: Περιορισμός Dz. (Για να αποτρέψετε την άκαμπτη κίνηση του σώματος στην κατεύθυνση Ζ) - Φορτία
Συμπυκνωμένο φορτίο, 1.0 Το lbf εφαρμόζεται στον κόμβο 1 στην κατεύθυνση Χ
Συμπυκνωμένο φορτίο, 1.0 Το lbf εφαρμόζεται στον κόμβο 73 στην κατεύθυνση -Y

Μοντέλο ανάλυσης
Αποτελέσματα
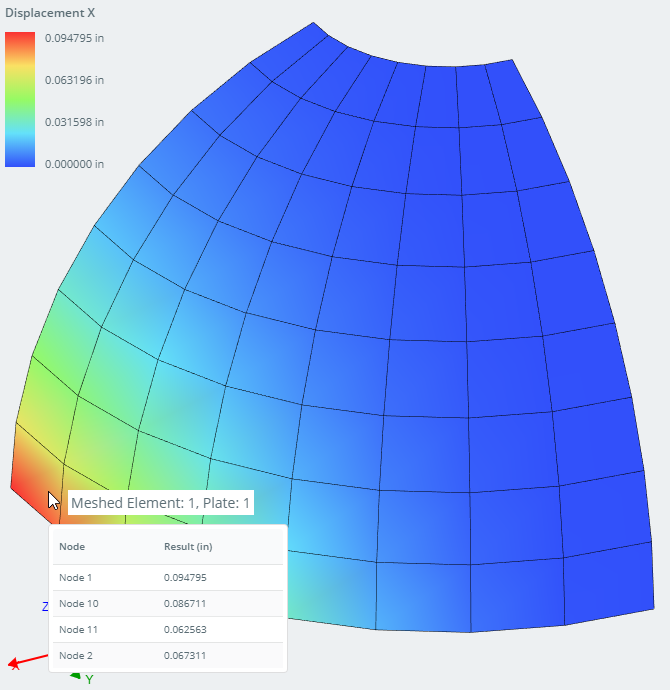
X-μετατοπίσεις της δομής (Κόμβος 1)
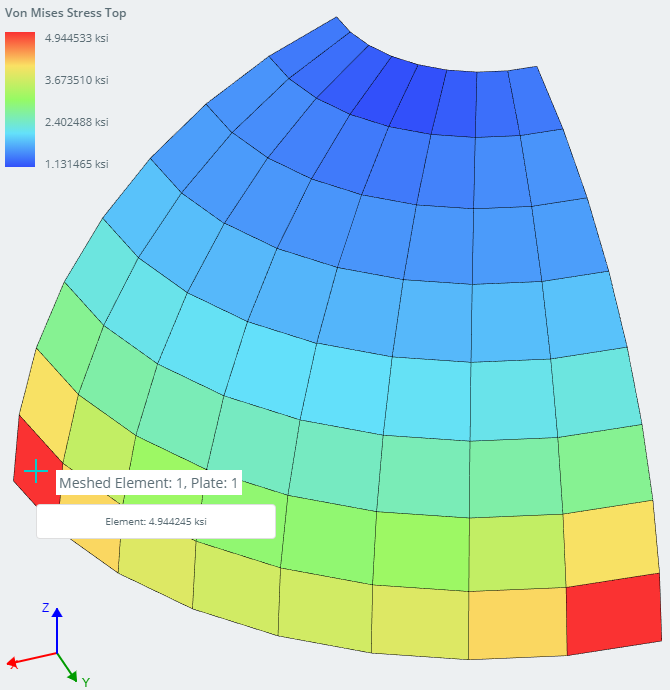
Von Mises Άγχος της δομής (Στοιχείο 2)
Σύγκριση αποτελεσμάτων
| Αποτέλεσμα | Τοποθεσία | SkyCiv | Θεωρητικός | Διαφορά 1 | Τρίτο μέρος 2 | Διαφορά 2 |
| Μέγιστη μετατόπιση X (σε) | Κόμβος 1 | 0.094795 | 0.094000 | 0.85% | 0.094789 | 0.01% |
| Max Von Mises Στρες – Στοιχείο (ksi) | Στοιχείο 1 Μπλουζα | 4.944245 | 4.989211 | 0.90% |
Αναφορά
MacNeal, Ρ. Η. και πιο σκληρό, Ρ. ΝΤΟ., “Προτεινόμενο τυπικό σύνολο προβλημάτων για τον έλεγχο της ακρίβειας πεπερασμένων στοιχείων”, Πεπερασμένα στοιχεία στην ανάλυση και το σχεδιασμό 1, 1985, σελ. 3-20, Βόρεια Ολλανδία.
Επιπλέον εκτιμήσεις
- Αυτό το μοντέλο επαλήθευσης δημιουργήθηκε και ελέγχθηκε 26 Απρίλιος 2020. Από αυτή την ημερομηνία, ο δίσκος επίλυσης δίσκων και το λογισμικό S3D μπορεί να έχουν βελτιωθεί περαιτέρω για να επιτευχθεί μεγαλύτερη ακρίβεια.
- Οι πλάκες δεν είναι ακριβή στοιχεία όπως δοκάρια και στοιχεία πλαισίου και επομένως το πλέγμα παίζει τεράστιο ρόλο στα αποτελέσματα. Προσπαθείτε πάντα να χρησιμοποιείτε ένα δομημένο πλέγμα όταν είναι δυνατόν να το κάνετε.
- Τα αποτελέσματα μεταξύ λογισμικού δεν θα είναι ποτέ τα ίδια, αφού χρησιμοποιούνται διαφορετικά στοιχεία και η φύση των πλακών είναι κατά προσέγγιση


