Σε σχεδιασμό σύνδεσης από χάλυβα, μπουλόνια σχεδιάζονται συνήθως ως μια ομάδα μπουλονιών που θα λειτουργήσει ως ένα σώμα για να αντισταθεί σε ένα δεδομένο φορτίο. Η αντοχή μιας ομάδας μπουλονιών συνήθως υπολογίζεται από την ισχύ ελέγχου του πιο κρίσιμου μπουλονιού της. Τα άμεσα φορτία κατανέμονται στον συνολικό αριθμό των μπουλονιών, ενώ η επαγόμενη ροπή λόγω της εκκεντρότητας των φορτίων κατανέμεται σε σχέση με τη ροπή αδράνειας της ομάδας μπουλονιών και την απόσταση από το κέντρο. Αυτή η ανάλυση ονομάζεται ελαστική ανάλυση. Λόγω των απλοποιημένων και συντηρητικών παραδοχών του για την κατανομή φορτίου, Συχνά δημιουργεί υπερβολικά σχεδιασμένες βιδωτές συνδέσεις.
Όταν μιλάμε για μηχανική αξίας και οικονομικά σχέδια, η ανελαστική προσέγγιση προτιμάται από τους περισσότερους κατασκευαστές. Απαιτεί μικρότερο αριθμό μπουλονιών για το ίδιο μέγεθος φορτίων. Να κάνουμε την ανελαστική προσέγγιση, το στιγμιαίο κέντρο περιστροφής (ICOR) μέθοδος που χρησιμοποιεί επαναλήψεις είναι ο καλύτερος τρόπος.
Σε αυτό το άρθρο, θα δείξουμε πώς να υπολογίσουμε την ισχύ του α βιδωτή σύνδεση χρησιμοποιώντας τη μέθοδο ICOR. Οι αντιδράσεις ανά μπουλόνι θα υπολογιστούν χρησιμοποιώντας την Εξίσωση (7-1) σε σελίδες 7-7 Αγοράστε το μοντέλο φόρτωσης τώρα Εγχειρίδιο AISC 15th Edition. Στη συνέχεια θα χρησιμοποιηθεί για να ελέγξει εάν η υποτιθέμενη θέση του στιγμιαίου κέντρου της ομάδας μπουλονιών είναι σωστή. Τελικά, μόλις έχουμε τη σωστή θέση IC, Στη συνέχεια θα υπολογίσουμε τον συντελεστή C της ομάδας μπουλονιών για να προσδιορίσουμε την αντοχή του.
Η χρήση της μεθόδου ICOR για τη λήψη του συντελεστή ομάδας μπουλονιών είναι μια μακρά διαδικασία, καθώς απαιτεί μια μέθοδο δοκιμής και σφάλματος για τη λήψη του Στιγμιαίου Κέντρου (IC) τοποθεσία. Στην εποχή μας, με τη χρήση επιλυτών υπολογιστών, το IC μιας ομάδας μπουλονιών μπορεί εύκολα να υπολογιστεί χρησιμοποιώντας προγραμματισμένες επαναλήψεις. Επίλυση ομάδας SkyCiv Bolt χρησιμοποιεί μια μέθοδο γρήγορης επανάληψης για να προσδιορίσει τη θέση IC και τον συντελεστή ομάδας μπουλονιών σε λίγα δευτερόλεπτα. Αυτή τη στιγμή εφαρμόζεται στο Α.Σ 4100 κώδικας σχεδίασης, αλλά σύντομα θα ενσωματωθεί στους υπόλοιπους κώδικες σχεδίασης.
Λήψη των ιδιοτήτων της ομάδας Bolt
Ας ξεκινήσουμε την απλή ανάλυσή μας σε μια ομάδα μπουλονιών τεσσάρων μπουλονιών φορτωμένων με έκκεντρο κατακόρυφο διατμητικό φορτίο 10 kips . Η εκκεντρότητα του φορτίου κατά τον άξονα x είναι 4 ίντσες στα δεξιά της ομάδας μπουλονιών. Η γωνία από την κατακόρυφο είναι μηδέν και η εκκεντρότητα κατά μήκος του άξονα y είναι μηδέν.
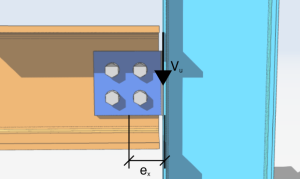
\(V_{εσύ} = 10 κιλά \)
\(\θήτα = 0 μοίρες)
\(μι_{Χ} = 4 σε)
\(μι_{και} = 0 in)
Το πρώτο πράγμα που πρέπει να κάνετε είναι να λάβετε τις συντεταγμένες όλων των μπουλονιών στην ομάδα μπουλονιών μας. Συνιστάται ιδιαίτερα η χρήση οπτικών οδηγών και πινάκων.
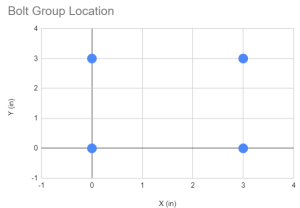
| Ταυτότητα καταστήματος | Χ (σε) | ΚΑΙ (σε) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
Για να πάρετε το κέντρο της ομάδας μπουλονιών κατά μήκος του x- και άξονες y, χρειαζόμαστε τον παρακάτω τύπο.
Αφήνω \(ν \) = συνολικός αριθμός μπουλονιών
\(Χ_{CG} = frac{\άθροισμα Χ}{ν}\)
\(Y_{CG} = frac{\άθροισμα Υ}{ν} \)
Τότε, η λύση μας είναι:
\(Χ_{CG} = frac{\άθροισμα Χ}{ν} = frac{0 σε + 0 σε + 3 σε + 3 σε}{4} = 1.5 σε)
\(Y_{CG} = frac{\άθροισμα Υ}{ν} = frac{0 σε + 3 σε + 0 σε + 3 σε}{4} = 1.5 σε)
Υποθέστε τη θέση του I.C.
Μετά τη λήψη του κέντρου, θα υποθέσουμε τη θέση του στιγμιαίου κέντρου \(IC). Σαν πρώτη προσπάθεια, μπορούμε να υποθέσουμε ότι το IC βρίσκεται στο γεωμετρικό κέντρο της ομάδας μπουλονιών.
Έτσι, υποθέτω
\(Χ_{IC} = X_{CG} = 1.5 σε)
\(Y_{IC} = Y_{CG} = 1.5 σε)
Τότε, καταγράφουμε τη μετατόπιση κάθε μπουλονιού στη θέση του IC. Μπορούμε απλά να το κάνουμε αυτό παίρνοντας πρώτα την απόσταση κατά μήκος του x και την απόσταση κατά μήκος του y, τότε λάβετε τη μετατόπισή του
| Ταυτότητα καταστήματος | cx (σε) | cy (σε) | ντο (σε) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
Οπου,
\(ντο_{Χ} = X_{Εγώ} – Χ_{IC}\)
\(ντο_{και} = Y_{Εγώ} – Y_{IC}\)
\(c = sqrt{{\αριστερά(ντο_{Χ} \σωστά)}^{2} + {\αριστερά(ντο_{και} \σωστά)}^{2}}\)
Για το μπουλόνι αρ. 1, η λύση μας είναι
\(ντο_{Χ} = 0 in – 1.5 σε = -1.5 σε)
\(ντο_{και} = 0 in – 1.5 σε = -1.5 σε)
\(c = sqrt{{\αριστερά( -1.5 στο δεξιά)}^{2} + {\αριστερά( -1.5 στο δεξιά)}^{2}} = 2.121in\)
Υπολογίστε την παραμόρφωση ανά απόσταση μπουλονιού από το IC
συνεπώς, αφού λάβετε τις αποστάσεις των μπουλονιών από την υποτιθέμενη θέση IC, Στη συνέχεια υπολογίζουμε την παραμόρφωση κάθε μπουλονιού ως συνάρτηση της απόστασής του.
Η μέγιστη παραμόρφωση ανά μπουλόνι, αριθμομηχανή φορτίου ανέμου \(\Δέλτα_{Μέγιστη} = 0.34 σε), βασίζεται σε πειραματικά δεδομένα για ένα μπουλόνι ASTM όπως περιγράφεται στη σελίδα AISC 7-8. Χρησιμοποιώντας γραμμική αναλογία, και ρύθμιση \(\Δέλτα_{Μέγιστη} = 0.34 σε), μπορούμε να υπολογίσουμε την παραμόρφωση ενός μεμονωμένου μπουλονιού σε σχέση με το τμήμα του στη μέγιστη απόσταση \(ντο_{Μέγιστη}\). Η εξίσωση για να πάρει φαίνεται παρακάτω.
\(\Δέλτα_{1} = 0,34 in φορές αριστερά( \frac{ντο}{ντο_{Μέγιστη}}\σωστά) \)
Για το μπουλόνι αρ. 1, η παραμόρφωση είναι
\(\Δέλτα_{1} = 0,34 in φορές αριστερά( \frac{2.121 σε}{2.121 σε}\σωστά)\)
Για τα υπόλοιπα μπουλόνια, Οι υπολογιζόμενες παραμορφώσεις παρατίθενται παρακάτω.
| Ταυτότητα καταστήματος | \(\Delta\) (σε) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Λάβετε τις αντιδράσεις ανά μπουλόνι
Αφού έχουμε την παραμόρφωση ανά μπουλόνι, μπορούμε στη συνέχεια να χρησιμοποιήσουμε το AISC 15th Ed. Εξ (7-1) για να λάβετε τις αντιδράσεις ανά μπουλόνι.
\(R = R_{τελ} \αριστερά ( 1 – ε ^{-10\Δέλτα}\σωστά )^{0.55}\)
ο \(R_{τελ}\) στην εξίσωση είναι το υποτιθέμενο τελικό φορτίο σε ένα μπουλόνι, την οποία μπορούμε να ορίσουμε ως αντοχή στη διάτμηση του μπουλονιού.
\(R_{τελ} = phi R_{ν} \)
Για το παράδειγμά μας, θα χρησιμοποιήσουμε διατμητική αντοχή μπουλονιού \(24.4 δέρμα μόσχου ακατέργαστου). Επιτρέπεται επίσης η χρήση άλλης τιμής, καθώς αυτή απλώς θα ακυρωθεί όταν υπολογίσουμε τον συντελεστή ομάδας μπουλονιών \(ΝΤΟ) αργότερα.
Για το μπουλόνι αρ. 1, η υπολογιζόμενη αντίδραση είναι
\(R = R_{τελ} \αριστερά ( 1 – ε ^{-10\Δέλτα}\σωστά )^{0.55}\)
\(R = 24.4 kip αριστερά ( 1 – ε ^{-10 \φορές αριστερά ( 0.34 στο δεξιά )}\σωστά )^{0.55}\)
\(R = 23.949 δέρμα μόσχου ακατέργαστου)
Για τα υπόλοιπα μπουλόνια, οι υπολογιζόμενες αντιδράσεις είναι οι εξής. Την ίδια στιγμή, τα συστατικά της αντίδρασης μπουλονιών \(R ) κατά μήκος των x και y φαίνονται επίσης.
| Ταυτότητα καταστήματος | Ρ (δέρμα μόσχου ακατέργαστου) | Rx (δέρμα μόσχου ακατέργαστου) | Ράι (δέρμα μόσχου ακατέργαστου) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
Για μπουλόνι Νο. 1, Οι λύσεις για τη λήψη των συνιστωσών x και y φαίνονται παρακάτω.
\(R_{Χ} = -R αριστερά ( \frac{ντο_{και}}{ντο} \σωστά ) = -23.949 \φορές αριστερά ( \frac{-1.5σε}{2.121σε} \σωστά ) = 23.949 δέρμα μόσχου ακατέργαστου)
\(R_{και} = R αριστερά ( \frac{ντο_{Χ}}{ντο} \σωστά ) = 23.949 \φορές αριστερά ( \frac{1.5σε}{2.121σε} \σωστά ) = 23.949 δέρμα μόσχου ακατέργαστου)
Εξάλλου, θα πρέπει να λάβουμε το επαγόμενο φορτίο ροπής ανά μπουλόνι λόγω της εκκεντρότητας. Για να το υπολογίσουμε αυτό, χρησιμοποιούμε τα εξαρτήματα \(R_{Χ}\) και \(R_{και}\) και να τις πολλαπλασιάσουμε με τις εκκεντρότητες \(ντο_{και}\) και \(ντο_{Χ}\), αντίστοιχα.
Για μπουλόνι Νο. 1, η στιγμή αντίδρασης στο IC είναι
\(Μ_{ρ} = -R_{Χ}ντο_{και} + -R_{και}ντο_{Χ} \)
\(Μ_{ρ} = -16.937 kip times αριστερά ( -1.5στο δεξιά) + -16.937 kip times αριστερά ( -1.5 στο δεξιά ) \)
\(Μ_{ρ} = 50.811 κοτόπουλο)
Για τα υπόλοιπα μπουλόνια, Οι αντίστοιχες αντιδράσεις στιγμής παρατίθενται παρακάτω.
| Ταυτότητα καταστήματος | κύριος (κοτόπουλο) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀Κύριος = 101.622 |
Επαλήθευση της θέσης IC
Τώρα που έχουμε τις αντιδράσεις διάτμησης και ροπής ανά μπουλόνι, θα το χρησιμοποιήσουμε για να προσδιορίσουμε την ποσότητα του φορτίου Pu στο οποίο αντιστέκεται αυτή η ομάδα μπουλονιών. Για να το κάνω αυτό, θα πάρουμε το αποτέλεσμα του αθροίσματος όλων των αντιδράσεων κατά μήκος του x και του αθροίσματος όλων των αντιδράσεων κατά μήκος του y.
Από την προηγούμενη ενότητα, το έχουμε υπολογίσει
\(\άθροισμα R_{Χ}=0kip\)
και
\(\άθροισμα R_{και}=0kip\)
Έτσι,
\(Π_{εσύ} = sqrt{{\αριστερά( \άθροισμα R_{Χ} \σωστά)}^{2} + {\αριστερά( \άθροισμα R_{και} \σωστά)}^{2}} = 0 δέρμα μόσχου ακατέργαστου)
Από το προκύπτον φορτίο \(Π_{εσύ} = 0 kip), μπορούμε να αποφασίσουμε σε αυτό το σημείο να μην προχωρήσουμε στην επαλήθευση αφού τα δεδομένα μας θα είναι απλώς μηδενικά. Μπορούμε επίσης να συμπεράνουμε ότι η πρώτη υποτιθέμενη θέση του I.C., που βρίσκεται στο κέντρο της ομάδας μπουλονιών, είναι λάθος. Ωστόσο, για τους σκοπούς αυτής της συζήτησης, θα προχωρήσουμε στα παρακάτω βήματα.
\(Π_{ux} = -P_{εσύ}αμαρτία αριστερά ( \θήτα σωστά ) = 0 δέρμα μόσχου ακατέργαστου \)
\(Π_{uy} = -P_{εσύ}cosαριστερά ( \θήτα σωστά ) = 0 δέρμα μόσχου ακατέργαστου \)
\(Μ_{εσύ} = -P_{ux}\αριστερά ( Y_{CG} + μι_{και} – Y_{IC} \σωστά ) + -Π_{uy} \αριστερά (Χ_{CG} + μι_{Χ} – Χ_{IC} \σωστά ) = 0 δέρμα μόσχου ακατέργαστου \)
Από,
\(Π_{ux} \neq sum R_{Χ} \)
\(Π_{uy} \neq sum R_{και} \)
\(Μ_{εσύ} \δεν ειμαι M_{ρ} \)
Επομένως, η υποτιθέμενη τοποθεσία του I.C. είναι λάθος. Μπορούμε τώρα να προχωρήσουμε στην επόμενη υποτιθέμενη τοποθεσία.
Το SkyCiv έχει πλήρη ενσωμάτωση του υπολογισμού της ομάδας μπουλονιών στην Αυστραλιανή Τυπική Μονάδα. Θέλετε να δοκιμάσετε το λογισμικό σχεδιασμού σύνδεσης?
Δεύτερη Επανάληψη
Για τη δεύτερη επανάληψη μας, ας υποθέσουμε ότι το I.C. βρίσκεται στις συντεταγμένες που φαίνονται παρακάτω.
Υποθέτω
\(Χ_{IC} = 0.062 σε)
\(Y_{IC} = 1.5 σε)
Τότε, ας κάνουμε τα βήματα που κάναμε στην πρώτη μας επανάληψη. Συνοψίζοντας, Ο παρακάτω πίνακας δείχνει τις συντεταγμένες, η απόσταση κάθε μπουλονιού από το υποτιθέμενο I.C, και την αντίστοιχη παραμόρφωση ως προς την απόσταση.
| Ταυτότητα καταστήματος | Χ (σε) | ΚΑΙ (σε) | cx (σε) | cy (σε) | ντο (σε) | \(\Delta\) (σε) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Σημειώστε ότι το υπολογιζόμενο κεντροειδές του ομάδα μπουλονιών εξακολουθεί να είναι το ίδιο, αφού τίποτα δεν έχει αλλάξει στις συντεταγμένες των μπουλονιών.
\(Χ_{CG} = 1.5 σε)
\(Y_{CG} = 1.5 σε)
Τότε, υπολογίζουμε τις αντιδράσεις κατά μήκος του x, αντιδράσεις κατά μήκος y, και την αντίστοιχη στιγμή. Οι τιμές παρατίθενται παρακάτω.
| Ταυτότητα καταστήματος | Ρ (δέρμα μόσχου ακατέργαστου) | Rx (δέρμα μόσχου ακατέργαστου) | Ράι (δέρμα μόσχου ακατέργαστου) | κύριος (κοτόπουλο) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀Κύριος = 222 |
Επόμενο, προσδιορίζουμε το προκύπτον φορτίο όλων των αντιδράσεων κατά μήκος των x και y.
\(Π_{εσύ} = sqrt{{\αριστερά( \άθροισμα R_{Χ} \σωστά)}^{2} + {\αριστερά( \άθροισμα R_{και} \σωστά)}^{2}}\)
\(Π_{εσύ} = sqrt{{\αριστερά( 0 kipright)}^{2} + {\αριστερά( 40.703 kipright)}^{2}}\)
\(Π_{εσύ} = 40.703 δέρμα μόσχου ακατέργαστου)
Τότε, τα συστατικά του προκύπτοντος φορτίου με βάση το δεδομένο \(\θήτα) φαίνεται παρακάτω.
\(Π_{ux} = -P_{εσύ}αμαρτία αριστερά ( \θήτα σωστά ) = -41kip times sin left ( 0 μοίρες δεξιά )= 0 δέρμα μόσχου ακατέργαστου)
\(Π_{uy} = -P_{εσύ}cos αριστερά ( \θήτα σωστά ) = -41kip times cos left ( 0 μοίρες δεξιά )= -41 δέρμα μόσχου ακατέργαστου)
Στη συνέχεια, θα χρησιμοποιήσουμε αυτά τα στοιχεία για να λύσουμε το στιγμιαίο φορτίο σχετικά με το υποτιθέμενο I.C.
\(Μ_{εσύ} = -P_{ux} \αριστερά ( Y_{CG} + μι_{και} – Y_{IC} \σωστά) + Π_{uy} \αριστερά ( Χ_{CG} + μι_{Χ} – Χ_{IC} \σωστά)\)
\(Μ_{εσύ} = -0 kip αριστερά ( 1.5 σε +0 σε – 1.5 στο δεξιά) + 41 kip αριστερά ( 1.5 σε +4 σε – 0.06 στο δεξιά)\)
\(Μ_{εσύ} = -222 κοτόπουλο)
Επόμενο, ας συγκρίνουμε το υπολογισμένο Πux, Πux, και Μεσύ στις αντιδράσεις της ομάδας μπουλονιών.
\(Π_{ux} \περίπου – \άθροισμα R_{Χ}\)
\(Π_{uy} \περίπου – \άθροισμα R_{και}\)
\(Μ_{εσύ} \περίπου – \άθροισμα M_{εσύ}\)
Δεδομένου ότι η αριστερή πλευρά είναι σχεδόν ίση με τη δεξιά πλευρά της εξίσωσης, μπορούμε να πούμε ότι η υποτιθέμενη θέση του Ι.Κ. είναι σωστό!
Επίλυση συντελεστή C
Μόλις το I.C. η τοποθεσία καθορίζεται, μπορούμε τώρα να πάρουμε τον συντελεστή ομάδας μπουλονιών C με τον παρακάτω τύπο.
\(C = frac{Π_{εσύ}}{\phi R_{ν}} = \frac{40.703 δέρμα μόσχου ακατέργαστου}{24.4 δέρμα μόσχου ακατέργαστου} = 1.668\)
Δωρεάν αριθμομηχανή Bolt Group
Ελέγξτε πώς σχεδιάζουμε τις βιδωτές συνδέσεις μας με αυτήν την προσέγγιση χρησιμοποιώντας τη δική μας Δωρεάν αριθμομηχανή σχεδίασης σύνδεσης χάλυβα! Για περισσότερη λειτουργικότητα, εγγραφείτε στο λογισμικό μας Structural 3D σήμερα για να ξεκινήσετε!


