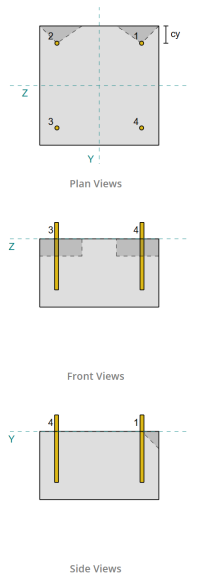
Παράδειγμα σχεδιασμού πλάκας βάσης χρησιμοποιώντας το EN 1993-1-8:2005, ΣΕ 1993-1-1:2005, ΣΕ 1992-1-1:2004, και EN 1992-4:2018.
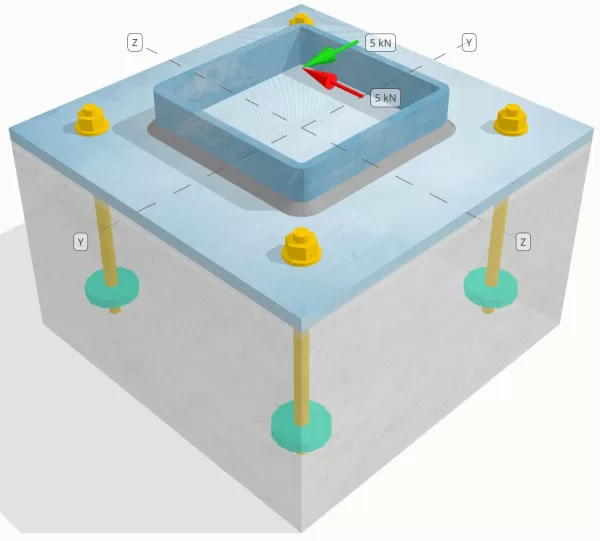
Προβληματική δήλωση
Προσδιορίστε εάν η σχεδιασμένη σύνδεση στήλης-πλάκας βάσης είναι επαρκής για α Vy=5-kN και Vz=5-kN φορτία διάτμησης.
Δεδομένα
Στήλη:
Ενότητα στήλης: SHS 180x180x8
Επιφάνεια στήλης: 5440 χιλ2
Υλικό στήλης: S235
Πλάκα βάσης:
Διαστάσεις πλάκας βάσης: 350 mm x 350 χιλ
Πάχος πλάκας βάσης: 12 χιλ
Υλικό πλάκας βάσης: S235
Πηκτώ:
Πάχος ενέματα: 6 χιλ
Υλικό ενέματος: ή σχισμές προεξέχουν πάνω από το ύψος των χαρακτηριστικών του ανάνερου εδάφους σε απόσταση 2 mi 30 MPa
Σκυρόδεμα:
Διαστάσεις σκυροδέματος: 350 mm x 350 χιλ
Πάχος σκυροδέματος: 350 χιλ
Σκυρόδεμα: C25/30
Ραγισμένα ή αδιευκρίνιστα: Ραγισμένος
Άγκυρες:
Διάμετρος άγκυρας: 12 χιλ
Αποτελεσματικό μήκος ενσωμάτωσης: 150 χιλ
Διάμετρος ενσωματωμένης πλάκας: 60 χιλ
Ενσωματωμένο πάχος πλάκας: 10 χιλ
Υλικό άγκυρας: 8.8
Άλλες πληροφορίες:
- Μη βυθισμένες άγκυρες.
- Άγκυρα με κομμένες κλωστές.
- Συντελεστής Κ7 για αστοχία διάτμησης χάλυβα αγκύρωσης: 1.0
- Βαθμός συγκράτησης στερέωσης: Κανένας περιορισμός
Συγκολλήσεις:
Τύπος συγκόλλησης: Συγκόλληση φιλέτου
Μέγεθος ποδιού συγκόλλησης: 8χιλ
Η ταξινόμηση μετάλλων πλήρωσης: Ε35
Δεδομένα αγκυροβόλησης (από Υπολογιστής Skyciv):
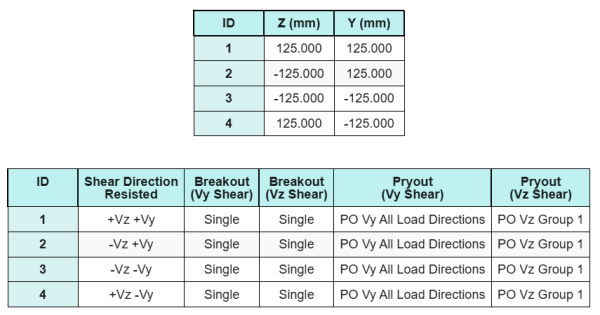
Μοντέλο στο δωρεάν εργαλείο SkyCiv
Μοντελοποιήστε το παραπάνω σχέδιο πλάκας βάσης χρησιμοποιώντας το δωρεάν διαδικτυακό μας εργαλείο σήμερα! Δεν απαιτείται εγγραφή.
Ορισμοί
Διαδρομή φόρτωσης:
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV ακολουθεί ΣΕ 1992-4:2018 για σχεδιασμό ράβδου αγκύρωσης. Τα διατμητικά φορτία που εφαρμόζονται στη στήλη μεταφέρονται στην πλάκα βάσης μέσω των συγκολλήσεων και στη συνέχεια στο σκυρόδεμα στήριξης μέσω των ράβδων αγκύρωσης. Οι ωτίδες τριβής και διάτμησης δεν λαμβάνονται υπόψη σε αυτό το παράδειγμα, καθώς αυτοί οι μηχανισμοί δεν υποστηρίζονται στο τρέχον λογισμικό.
Ομάδες άγκυρας:
Το λογισμικό περιλαμβάνει μια διαισθητική δυνατότητα που προσδιορίζει ποιες αγκυρώσεις αποτελούν μέρος μιας ομάδας αγκύρωσης για αξιολόγηση διάτμηση σκυροδέματος και διάτμηση σκυροδέματος αποτυχία.
Ενα ομάδα άγκυρας ορίζεται ως δύο ή περισσότερες άγκυρες με επικαλυπτόμενες περιοχές προβαλλόμενης αντίστασης. Σε αυτήν την περίπτωση, οι άγκυρες δρουν μαζί, και η συνδυασμένη αντίστασή τους ελέγχεται έναντι του εφαρμοζόμενου φορτίου στην ομάδα.
ΕΝΑ μονή άγκυρα ορίζεται ως μια άγκυρα της οποίας η περιοχή προβαλλόμενης αντίστασης δεν επικαλύπτεται με καμία άλλη. Σε αυτήν την περίπτωση, η άγκυρα ενεργεί μόνη της, και η εφαρμοζόμενη διατμητική δύναμη σε αυτή την άγκυρα ελέγχεται απευθείας έναντι της ατομικής της αντίστασης.
Αυτή η διάκριση επιτρέπει στο λογισμικό να καταγράφει τόσο τη συμπεριφορά της ομάδας όσο και την ατομική απόδοση αγκύρωσης κατά την αξιολόγηση των τρόπων αστοχίας που σχετίζονται με τη διάτμηση.
Υπολογισμοί βήμα προς βήμα
Ελεγχος #1: Υπολογίστε τη χωρητικότητα συγκόλλησης
Υποθέτουμε ότι το Vz το διατμητικό φορτίο αντιστέκεται από το πάνω και κάτω συγκολλήσεις, ενώ το Εσείς Το διατμητικό φορτίο αντιστέκεται αποκλειστικά από το αριστερές και δεξιές συγκολλήσεις.
Για τον προσδιορισμό της ικανότητας συγκόλλησης του πάνω και κάτω συγκολλήσεις, υπολογίζουμε πρώτα τους συνολικά μήκη συγκόλλησης.
\(
ΜΕΓΑΛΟ_{β,top\&κάτω μέρος} = 2 \αριστερά(αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{διάσελο} – 2αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{διάσελο} – 2r_{διάσελο}\σωστά)
= 2 \φορές αριστερά(180 \,\κείμενο{χιλ} – 2 \φορές 8 \,\κείμενο{χιλ} – 2 \φορές 4 \,\κείμενο{χιλ}\σωστά)
= 312 \,\κείμενο{χιλ}
\)
Επόμενο, υπολογίζουμε το καταπονήσεις στις συγκολλήσεις.
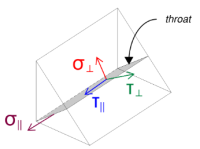
Σημειώστε ότι η εφαρμοζόμενη διάτμηση Vz δρα παράλληλα με τον άξονα συγκόλλησης, χωρίς να υπάρχουν άλλες δυνάμεις. Αυτό σημαίνει ότι οι κάθετες τάσεις μπορούν να ληφθούν ως μηδέν, και μόνο το διατμητική τάση στην παράλληλη διεύθυνση πρέπει να υπολογιστεί.
\(
\σίγμα{\αδ} = frac{Ν}{(ΜΕΓΑΛΟ_{β,top\&κάτω μέρος})\,a\sqrt{2}}
= frac{0 \,\κείμενο{ΚΝ}}{(312 \,\κείμενο{χιλ}) \φορές 5.657 \,\κείμενο{χιλ} \φορές sqrt{2}}
= 0
\)
\(
\τα δικα σου_{\αδ} = frac{0}{(ΜΕΓΑΛΟ_{β,top\&κάτω μέρος})\,a\sqrt{2}}
= frac{0 \,\κείμενο{ΚΝ}}{(312 \,\κείμενο{χιλ}) \φορές 5.657 \,\κείμενο{χιλ} \φορές sqrt{2}}
= 0
\)
\(
\τα δικα σου_{\παράλληλο} = frac{V_{με}}{(ΜΕΓΑΛΟ_{β,top\&κάτω μέρος})\,ένα}
= frac{5 \,\κείμενο{ΚΝ}}{(312 \,\κείμενο{χιλ}) \φορές 5.657 \,\κείμενο{χιλ}}
= 2.8329 \,\κείμενο{MPa}
\)
Χρησιμοποιώντας ΣΕ 1993-1-8:2005, Εξ. 4.1, η σχεδιαστική τάση συγκόλλησης λαμβάνεται με τη μέθοδο της κατεύθυνσης.
\(
ΦΑ_{β,Ed1} = sqrt{ (\σίγμα{\αδ})^ 2 + 3 \αριστερά( (\τα δικα σου_{\αδ})^ 2 + (\τα δικα σου_{\παράλληλο})^2 right) }
= sqrt{ (0)^ 2 + 3 \φορές αριστερά( (0)^ 2 + (2.8329 \,\κείμενο{MPa})^2 right) }
= 4.9067 \,\κείμενο{MPa}
\)
Επιπλέον, η κανονική τάση σχεδιασμού για τον έλεγχο του βασικού μετάλλου, ανά ΣΕ 1993-1-8:2005, Εξ. 4.1, λαμβάνεται ως μηδέν, Από κανένα φυσιολογικό άγχος είναι παρούσα.
\(
ΦΑ_{β,Ed2} = \sigma_{\αδ} = 0
\)
Τώρα, ας αξιολογήσουμε το αριστερές και δεξιές συγκολλήσεις. Όπως και με τις συγκολλήσεις πάνω και κάτω, υπολογίζουμε πρώτα το Συνολικό μήκος συγκόλλησης.
\(
ΜΕΓΑΛΟ_{β,left\&σωστά} = 2 \αριστερά(ρε_{διάσελο} – 2αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{διάσελο} – 2r_{διάσελο}\σωστά)
= 2 \φορές αριστερά(180 \,\κείμενο{χιλ} – 2 \φορές 8 \,\κείμενο{χιλ} – 2 \φορές 4 \,\κείμενο{χιλ}\σωστά)
= 312 \,\κείμενο{χιλ}
\)
Στη συνέχεια υπολογίζουμε τα συστατικά του τάσεις συγκόλλησης.
\(
\σίγμα{\αδ} = frac{Ν}{(ΜΕΓΑΛΟ_{β,left\&σωστά})\,a\sqrt{2}}
= frac{0 \,\κείμενο{ΚΝ}}{(312 \,\κείμενο{χιλ}) \φορές 5.657 \,\κείμενο{χιλ} \φορές sqrt{2}}
= 0
\)
\(
\τα δικα σου_{\αδ} = frac{0}{(ΜΕΓΑΛΟ_{β,left\&σωστά})\,a\sqrt{2}}
= frac{0 \,\κείμενο{ΚΝ}}{(312 \,\κείμενο{χιλ}) \φορές 5.657 \,\κείμενο{χιλ} \φορές sqrt{2}}
= 0
\)
\(
\τα δικα σου_{\παράλληλο} = frac{V_y}{(ΜΕΓΑΛΟ_{β,left\&σωστά})\,ένα}
= frac{5 \,\κείμενο{ΚΝ}}{(312 \,\κείμενο{χιλ}) \φορές 5.657 \,\κείμενο{χιλ}}
= 2.8329 \,\κείμενο{MPa}
\)
Χρησιμοποιώντας ΣΕ 1993-1-8:2005, Εξ. 4.1, προσδιορίζουμε τόσο την σχεδιαστική τάση συγκόλλησης όσο και την κανονική τάση σχεδιασμού για τον έλεγχο του βασικού μετάλλου.
\(
ΦΑ_{β,Ed1} = sqrt{ \αριστερά( \σίγμα{\αδ} \σωστά)^ 2 + 3 \αριστερά( \αριστερά( \τα δικα σου_{\αδ} \σωστά)^ 2 + \αριστερά( \τα δικα σου_{\παράλληλο} \σωστά)^2 right) }
\)
\(
ΦΑ_{β,Ed1} = sqrt{ \αριστερά( 0 \σωστά)^ 2 + 3 \φορές αριστερά( \αριστερά( 0 \σωστά)^ 2 + \αριστερά( 2.8329 \,\κείμενο{MPa} \σωστά)^2 right) }
\)
\(
ΦΑ_{β,Ed1} = 4.9067 \,\κείμενο{MPa}
\)
Το επόμενο βήμα είναι η αναγνώριση του που διέπει την τάση συγκόλλησης μεταξύ των άνω/κάτω συγκολλήσεων και των αριστερών/δεξιών συγκολλήσεων. Επειδή τα μήκη συγκόλλησης είναι ίσα και τα εφαρμοζόμενα φορτία έχουν το ίδιο μέγεθος, οι τάσεις συγκόλλησης που προκύπτουν είναι ίσες.
\(
ΦΑ_{β,Ed1} = \max(ΦΑ_{β,Ed1}, \, ΦΑ_{β,Ed1})
= \max(4.9067 \,\κείμενο{MPa}, \, 4.9067 \,\κείμενο{MPa})
= 4.9067 \,\κείμενο{MPa}
\)
Η τάση του βασικού μετάλλου παραμένει μηδενική.
\(
ΦΑ_{β,Ed2} = \max(ΦΑ_{β,Ed2}, \, ΦΑ_{β,Ed2}) = \max(0, \, 0) = 0
\)
Τώρα, υπολογίζουμε την ικανότητα συγκόλλησης. Πρώτα, η αντίσταση του συγκόλληση φιλέτου υπολογίζεται. Τότε, η αντίσταση του βασικό μέταλλο καθορίζεται. Χρησιμοποιώντας EN 1993-1-8:2005, Εξ. 4.1, οι χωρητικότητες υπολογίζονται ως εξής:
\(
ΦΑ_{β,Rd1} = frac{f_u}{\beta_w \left(\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Μ2, συγκόλληση}\σωστά)}
= frac{360 \,\κείμενο{MPa}}{0.8 \φορές (1.25)}
= 360 \,\κείμενο{MPa}
\)
\(
ΦΑ_{β,Rd2} = frac{0.9 f_u}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Μ2, συγκόλληση}}
= frac{0.9 \φορές 360 \,\κείμενο{MPa}}{1.25}
= 259.2 \,\κείμενο{MPa}
\)
Τελικά, Συγκρίνουμε τις τάσεις συγκόλλησης με τις ικανότητες συγκόλλησης, και το βασικό μέταλλο καταπονείται με τις χωρητικότητες των βασικών μετάλλων.
Από 4.9067 MPa < 360 MPa και 0 MPa < 259.2 MPa, η χωρητικότητα της συγκολλημένης σύνδεσης είναι επαρκής.
Ελεγχος #2: Υπολογίστε την ικανότητα διάσπασης σκυροδέματος λόγω διάτμησης Vy
Κατόπιν των διατάξεων του ΣΕ 1992-4:2018, Το κάθετο άκρο στο εφαρμοζόμενο φορτίο εκτιμάται για αστοχία διάτμησης. Μόνο το άγκυρες πλησιέστερα σε αυτή την άκρη θεωρούνται αρραβωνιασμένοι, ενώ οι υπόλοιπες άγκυρες θεωρείται ότι δεν αντέχουν στη διάτμηση.
Αυτές οι αγκυρώσεις άκρων πρέπει να έχουν απόσταση από άκρο σκυροδέματος μεγαλύτερη από τη μεγαλύτερη των 10·hef και 60·d, όπου έχω είναι το μήκος ενσωμάτωσης και ρε είναι η διάμετρος της άγκυρας. Εάν δεν πληρούται αυτή η προϋπόθεση, το πάχος της πλάκας βάσης πρέπει να είναι μικρότερο από 0,25·hef.
Εάν οι απαιτήσεις σε ΣΕ 1992-4:2018, Ρήτρα 7.2.2.5(1), δεν είναι ικανοποιημένοι, το λογισμικό SkyCiv δεν μπορεί να προχωρήσει στους ελέγχους σχεδιασμού, και συνιστάται στον χρήστη να ανατρέξει σε άλλα σχετικά πρότυπα.

Από τα αποτελέσματα του λογισμικού SkyCiv, οι αγκυρώσεις των άκρων λειτουργούν ως άγκυρες, αφού οι προβλεπόμενες περιοχές τους δεν αλληλεπικαλύπτονται. Για αυτόν τον υπολογισμό, Αγκυρα 1 θα ληφθούν υπόψη.
Για να υπολογίσετε το τμήμα του διατμητικού φορτίου Vy που μεταφέρει η Anchor 1, η συνολική διάτμηση Vy κατανέμεται μεταξύ των αγκυρώσεων που βρίσκονται πλησιέστερα στην άκρη. Αυτό δίνει το κάθετη δύναμη στο Anchor 1.
\(
V_{\αδ} = frac{V_y}{n_{ένα,μικρό}}
= frac{5 \,\κείμενο{ΚΝ}}{2}
= 2.5 \,\κείμενο{ΚΝ}
\)
Για το παράλληλη δύναμη, Υποτίθεται ότι όλες οι αγκυρώσεις αντιστέκονται εξίσου στο φορτίο. Επομένως, η παράλληλη συνιστώσα του φορτίου υπολογίζεται ως:
\(
V_{\παράλληλο} = frac{V_z}{n_{Α.Κ.}}
= frac{5 \,\κείμενο{ΚΝ}}{4}
= 1.25 \,\κείμενο{ΚΝ}
\)
ο συνολικό διατμητικό φορτίο στο Anchor 1 είναι επομένως:
\(
V_{Εκδ} = sqrt{ \αριστερά( V_{\αδ} \σωστά)^ 2 + \αριστερά( V_{\παράλληλο} \σωστά)^ 2 }
\)
\(
V_{Εκδ} = sqrt{ \αριστερά( 2.5 \,\κείμενο{ΚΝ} \σωστά)^ 2 + \αριστερά( 1.25 \,\κείμενο{ΚΝ} \σωστά)^ 2 } = 2.7951 \,\κείμενο{ΚΝ}
\)
Το πρώτο μέρος του υπολογισμού της χωρητικότητας είναι να προσδιοριστεί η παράγοντες άλφα και βήτα. Χρησιμοποιούμε ΣΕ 1992-4:2018, Ρήτρα 7.2.2.5, να ρυθμίσετε το lf διάσταση, και Εξισώσεις 7.42 και 7.43 για τον προσδιορισμό των παραγόντων.
\(
l_f = \min(ω_{εφ}, \, 12ρε_{Α.Κ.})
= min(150 \,\κείμενο{χιλ}, \, 12 \φορές 12 \,\κείμενο{χιλ})
= 144 \,\κείμενο{χιλ}
\)
\(
\άλφα = 0.1 \αριστερά(\frac{l_f}{ντο_{1,s1}}\σωστά)^{0.5}
= 0.1 \φορές αριστερά(\frac{144 \,\κείμενο{χιλ}}{50 \,\κείμενο{χιλ}}\σωστά)^{0.5}
= 0.16971
\)
\(
\βήτα = 0.1 \αριστερά(\frac{ρε_{Α.Κ.}}{ντο_{1,s1}}\σωστά)^{0.2}
= 0.1 \φορές αριστερά(\frac{12 \,\κείμενο{χιλ}}{50 \,\κείμενο{χιλ}}\σωστά)^{0.2}
= 0.07517
\)
Το επόμενο βήμα είναι ο υπολογισμός του αρχική τιμή της χαρακτηριστικής αντίστασης του συνδετήρα. Χρησιμοποιώντας ΣΕ 1992-4:2018, Εξίσωση 7.41, η τιμή είναι:
\(
V^{0}_{Rk,ντο} = k_9 \left( \frac{ρε_{Α.Κ.}}{\κείμενο{χιλ}} \σωστά)^{\άλφα}
\αριστερά( \frac{l_f}{\κείμενο{χιλ}} \σωστά)^{\βήτα}
\τ.μ.{ \frac{φά_{ck}}{\κείμενο{MPa}} }
\αριστερά( \frac{ντο_{1,s1}}{\κείμενο{χιλ}} \σωστά)^{1.5} Ν
\)
\(
V^{0}_{Rk,ντο} = 1.7 \φορές αριστερά( \frac{12 \,\κείμενο{χιλ}}{1 \,\κείμενο{χιλ}} \σωστά)^{0.16971}
\φορές αριστερά( \frac{144 \,\κείμενο{χιλ}}{1 \,\κείμενο{χιλ}} \σωστά)^{0.07517}
\φορές sqrt{ \frac{20 \,\κείμενο{MPa}}{1 \,\κείμενο{MPa}} }
\φορές αριστερά( \frac{50 \,\κείμενο{χιλ}}{1 \,\κείμενο{χιλ}} \σωστά)^{1.5}
\φορές 0.001 \,\κείμενο{ΚΝ}
\)
\(
V^{0}_{Rk,ντο} = 5.954 \,\κείμενο{ΚΝ}
\)
Τότε, Υπολογίζουμε το προβλεπόμενη περιοχή αναφοράς μιας μόνο άγκυρας, ΕΠΟΜΕΝΟ ΣΕ 1992-4:2018, Εξίσωση 7.44.
\(
ΕΝΑ_{ντο,Β}^{0} = 4.5 \αριστερά( ντο_{1,s1} \σωστά)^ 2
= 4.5 \φορές αριστερά( 50 \,\κείμενο{χιλ} \σωστά)^ 2
= 11250 \,\κείμενο{χιλ}^ 2
\)
Μετά από αυτό, Υπολογίζουμε το πραγματική προβλεπόμενη περιοχή της Άγκυρας 1.
\(
ΣΙ_{ντο,Β} = min(ντο_{αριστερά,s1}, \, 1.5ντο_{1,s1}) + \ελάχ(ντο_{σωστά,s1}, \, 1.5ντο_{1,s1})
\)
\(
ΣΙ_{ντο,Β} = min(300 \,\κείμενο{χιλ}, \, 1.5 \φορές 50 \,\κείμενο{χιλ}) + \ελάχ(50 \,\κείμενο{χιλ}, \, 1.5 \φορές 50 \,\κείμενο{χιλ}) = 125 \,\κείμενο{χιλ}
\)
\(
η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{ντο,Β} = min(1.5ντο_{1,s1}, \, αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{σύμπλεγμα}) = min(1.5 \φορές 50 \,\κείμενο{χιλ}, \, 200 \,\κείμενο{χιλ}) = 75 \,\κείμενο{χιλ}
\)
\(
ΕΝΑ_{ντο,Β} = H_{ντο,Β} ΣΙ_{ντο,Β} = 75 \,\κείμενο{χιλ} \φορές 125 \,\κείμενο{χιλ} = 9375 \,\κείμενο{χιλ}^ 2
\)
Πρέπει επίσης να υπολογίσουμε τις παραμέτρους για διάτμηση. Χρησιμοποιούμε ΣΕ 1992-4:2018, Εξίσωση 7.4, για να λάβετε τον παράγοντα που αντιπροσωπεύει το διαταραχή της κατανομής του στρες, Εξίσωση 7.46 για τον παράγοντα που αντιπροσωπεύει το πάχος μέλους, και Εξίσωση 7.48 για τον παράγοντα που αντιπροσωπεύει το επίδραση διατμητικού φορτίου κεκλιμένου προς την άκρη. Αυτά υπολογίζονται ως εξής:
\(
\Psi_{μικρό,Β} = min αριστερά( 0.7 + 0.3 \αριστερά( \frac{ντο_{2,s1}}{1.5ντο_{1,s1}} \σωστά), \, 1.0 \σωστά)
= min αριστερά( 0.7 + 0.3 \φορές αριστερά( \frac{50 \,\κείμενο{χιλ}}{1.5 \φορές 50 \,\κείμενο{χιλ}} \σωστά), \, 1 \σωστά)
= 0.9
\)
\(
\Psi_{η,Β} = max αριστερά( \αριστερά( \frac{1.5ντο_{1,s1}}{αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{σύμπλεγμα}} \σωστά)^{0.5}, \, 1 \σωστά)
= max αριστερά( \αριστερά( \frac{1.5 \φορές 50 \,\κείμενο{χιλ}}{200 \,\κείμενο{χιλ}} \σωστά)^{0.5}, \, 1 \σωστά)
= 1
\)
\(
\άλφα_{Β} = \tan^{-1} \αριστερά( \frac{V_{\παράλληλο}}{V_{\αδ}} \σωστά)
= \tan^{-1} \αριστερά( \frac{1.25 \,\κείμενο{ΚΝ}}{2.5 \,\κείμενο{ΚΝ}} \σωστά)
= 0.46365 \,\κείμενο{rad}
\)
\(
\Psi_{\άλφα,Β} = max αριστερά(
\τ.μ.{ \frac{1}{(\συν(\άλφα_{Β}))^ 2 + \αριστερά( 0.5 \, (\χωρίς(\άλφα_{Β})) \σωστά)^ 2 } }, \, 1 \σωστά)
\)
\(
\Psi_{\άλφα,Β} = max αριστερά(
\τ.μ.{ \frac{1}{(\συν(0.46365 \,\κείμενο{rad}))^ 2 + \αριστερά( 0.5 \times \sin(0.46365 \,\κείμενο{rad}) \σωστά)^ 2 } }, \, 1 \σωστά)
\)
\(
\Psi_{\άλφα,Β} = 1.0847
\)
Μια σημαντική σημείωση κατά τον προσδιορισμό του παράγοντα άλφα είναι να διασφαλιστεί ότι η κάθετη και η παράλληλη διάτμηση αναγνωρίζονται σωστά.
Τελικά, Υπολογίζουμε το αντίσταση σε διάσπαση της μονής άγκυρας χρησιμοποιώντας ΣΕ 1992-4:2018, Εξίσωση 7.1.
\(
V_{Rk,ντο} = V^0_{Rk,ντο} \αριστερά(\frac{ΕΝΑ_{ντο,Β}}{A^0_{ντο,Β}}\σωστά)
\Psi_{μικρό,Β} \Psi_{η,Β} \Psi_{εκ,Β} \Psi_{\άλφα,Β} \Psi_{σχετικά με,Β}
\)
\(
V_{Rk,ντο} = 5.954 \,\κείμενο{ΚΝ} \φορές αριστερά(\frac{9375 \,\κείμενο{χιλ}^ 2}{11250 \,\κείμενο{χιλ}^ 2}\σωστά)
\φορές 0.9 \φορές 1 \φορές 1 \φορές 1.0847 \φορές 1
= 4.8435 \,\κείμενο{ΚΝ}
\)
Εφαρμογή του μερικού παράγοντα, η σχεδιαστική αντίσταση είναι 3.23 ΚΝ.
\(
V_{Rd,ντο} = frac{V_{Rk,ντο}}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Mc}}
= frac{4.8435 \,\κείμενο{ΚΝ}}{1.5}
= 3.229 \,\κείμενο{ΚΝ}
\)
Από 2.7951 ΚΝ < 3.229 ΚΝ, η ικανότητα διάτμησης για διάτμηση Vy είναι επαρκής.
Ελεγχος #3: Υπολογίστε την ικανότητα διάσπασης σκυροδέματος λόγω διάτμησης Vz
Η ίδια προσέγγιση χρησιμοποιείται για τον προσδιορισμό της χωρητικότητας στο άκρο κάθετο στη διάτμηση Vz.

Λόγω του συμμετρικού σχεδιασμού, Οι άγκυρες που αντιστέκονται στη διάτμηση Vz προσδιορίζονται επίσης ως άγκυρες. Ας αναλογιστούμε Αγκυρα 1 και πάλι για τους υπολογισμούς.
Για να υπολογίσετε το κάθετο φορτίο στο Anchor 1, Διαιρούμε τη διάτμηση Vz με τον συνολικό αριθμό των αγκυρώσεων που βρίσκονται πιο κοντά στην άκρη μόνο. Για να υπολογίσετε το παράλληλο φορτίο στο Anchor 1, διαιρούμε τη διάτμηση Vy με τον συνολικό αριθμό των αγκυρώσεων.
\(
V_{\αδ} = frac{V_{με}}{n_{ένα,μικρό}}
= frac{5 \,\κείμενο{ΚΝ}}{2}
= 2.5 \,\κείμενο{ΚΝ}
\)
\(
V_{\παράλληλο} = frac{V_{και}}{n_{Α.Κ.}}
= frac{5 \,\κείμενο{ΚΝ}}{4}
= 1.25 \,\κείμενο{ΚΝ}
\)
\(
V_{Εκδ} = sqrt{ \αριστερά( V_{\αδ} \σωστά)^ 2 + \αριστερά( V_{\παράλληλο} \σωστά)^ 2 }
\)
\(
V_{Εκδ} = sqrt{ \αριστερά( 2.5 \,\κείμενο{ΚΝ} \σωστά)^ 2 + \αριστερά( 1.25 \,\κείμενο{ΚΝ} \σωστά)^ 2 }
= 2.7951 \,\κείμενο{ΚΝ}
\)
Χρησιμοποιώντας παρόμοια προσέγγιση στο Check #2, το προκύπτον αντίσταση σε διάσπαση για την ακμή κάθετη στη διάτμηση Vz είναι:
\(
V_{Rd,ντο} = frac{V_{Rk,ντο}}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Mc}}
= frac{4.8435 \,\κείμενο{ΚΝ}}{1.5}
= 3.229 \,\κείμενο{ΚΝ}
\)
Από 2.7951 ΚΝ < 3.229 ΚΝ, η ικανότητα διάτμησης για διάτμηση Vz είναι επαρκής.
Ελεγχος #4: Υπολογίστε την ικανότητα εκτόξευσης σκυροδέματος
Ο υπολογισμός για το αντίσταση διάτμησης περιλαμβάνει τον προσδιορισμό του ονομαστική χωρητικότητα των αγκυρίων έναντι διαρροής τάσης. Η αναφορά για την ικανότητα διάσπασης τάσης είναι ΣΕ 1992-4:2018, Ρήτρα 7.2.1.4. Μια λεπτομερής συζήτηση για την έκρηξη της έντασης καλύπτεται ήδη στο Παράδειγμα σχεδίασης SkyCiv με φορτίο τάσης και δεν θα επαναληφθεί σε αυτό το παράδειγμα σχεδίασης.
Από τους υπολογισμούς του λογισμικού SkyCiv, η ονομαστική χωρητικότητα του τμήματος για διάσπαση τάσης είναι 44.61 ΚΝ.
Στη συνέχεια χρησιμοποιούμε ΣΕ 1992-4:2018, Εξίσωση 7.39α, για να αποκτήσετε τη σχεδιαστική χαρακτηριστική αντίσταση. Χρησιμοποιώντας k8 = 2, η χωρητικότητα είναι 59.48 ΚΝ.
\(
V_{Rd,cp} = frac{k_8 N_{cbg}}{\Gamma_c}
= frac{2 \φορές 44.608 \,\κείμενο{ΚΝ}}{1.5}
= 59.478 \,\κείμενο{ΚΝ}
\)
Στον έλεγχο διάτμησης, όλες οι άγκυρες είναι αποτελεσματικές στην αντίσταση στο πλήρες διατμητικό φορτίο. Από την εικόνα που δημιουργήθηκε από το λογισμικό SkyCiv, όλες οι προβολές του κώνου αστοχίας επικαλύπτονται μεταξύ τους, κάνοντας τις άγκυρες να λειτουργούν ως ομάδα άγκυρας.

Επομένως, η απαιτούμενη αντίσταση της ομάδας αγκύρωσης είναι το συνολικό προκύπτον διατμητικό φορτίο του 7.07 ΚΝ.
\(
V_{res} = sqrt{(V_y)^ 2 + (V_z)^ 2}
= sqrt{(5 \,\κείμενο{ΚΝ})^ 2 + (5 \,\κείμενο{ΚΝ})^ 2}
= 7.0711 \,\κείμενο{ΚΝ}
\)
\(
V_{Εκδ} = αριστερά(\frac{V_{res}}{n_{Α.Κ.}}\σωστά) n_{ένα,G1}
= αριστερά(\frac{7.0711 \,\κείμενο{ΚΝ}}{4}\σωστά) \φορές 4
= 7.0711 \,\κείμενο{ΚΝ}
\)
Από 7.0711 ΚΝ < 59.478 ΚΝ, η ικανότητα διάτμησης είναι επαρκής.
Ελεγχος #5: Υπολογίστε την ικανότητα διάτμησης της ράβδου αγκύρωσης
Ο υπολογισμός της διατμητικής ικανότητας της ράβδου αγκύρωσης εξαρτάται από το εάν το διατμητικό φορτίο εφαρμόζεται με βραχίονα ροπής. Για να προσδιοριστεί αυτό, αναφερόμαστε ΣΕ 1992-4:2018, Ρήτρα 6.2.2.3, όπου το πάχος και το υλικό του ενέματος, τον αριθμό των συνδετήρων στο σχέδιο, την απόσταση των συνδετήρων, και άλλοι παράγοντες ελέγχονται.
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV πραγματοποιεί όλους τους απαραίτητους ελέγχους για να διαπιστώσει εάν η Το διατμητικό φορτίο δρα με ή χωρίς μοχλοβραχίονα. Για αυτό το παράδειγμα σχεδίασης, προσδιορίζεται ότι το διατμητικό φορτίο είναι δεν εφαρμόζεται με μοχλό βραχίονα. Επομένως, χρησιμοποιούμε ΣΕ 1992-4:2018, Ρήτρα 7.2.2.3.1, για τις εξισώσεις χωρητικότητας.
Ξεκινάμε υπολογίζοντας τη χαρακτηριστική αντίσταση του χαλύβδινου συνδετήρα χρησιμοποιώντας ΣΕ 1992-4:2018, Εξίσωση 7.34.
\(
V^0_{Rk,μικρό} = k_6 A_s f_{εσύ,Α.Κ.}
= 0.5 \φορές 113.1 \,\κείμενο{χιλ}^2 φορές 800 \,\κείμενο{MPa}
= 45.239 \,\κείμενο{ΚΝ}
\)
Επόμενο, εφαρμόζουμε τον παράγοντα για το εύπλαστο της μονής άγκυρας ή της ομάδας άγκυρας, λήψη k7 = 1.
\(
V_{Rk,μικρό} = k_7 V^{0}_{Rk,μικρό}
= 1 \φορές 45.239 \,\κείμενο{ΚΝ}
= 45.239 \,\κείμενο{ΚΝ}
\)
Στη συνέχεια λαμβάνουμε το μερικός παράγοντας για αστοχία διάτμησης χάλυβα χρησιμοποιώντας ΣΕ 1992-4:2018, Τραπέζι 4.1. Για μια άγκυρα με 8.8 υλικό, ο μερικός παράγοντας που προκύπτει είναι:
\(
\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Κυρία,κουρεύω}
= max αριστερά( 1.0 \αριστερά( \frac{ΦΑ_{εσύ,Α.Κ.}}{ΦΑ_{και,Α.Κ.}} \σωστά), \, 1.25 \σωστά)
= max αριστερά( 1 \[object Window]{800 \,\κείμενο{MPa}}{640 \,\κείμενο{MPa}}, \, 1.25 \σωστά)
= 1.25
\)
Εφαρμογή αυτού του παράγοντα στη χαρακτηριστική αντίσταση, η σχεδιαστική αντίσταση είναι 36.19 ΚΝ.
\(
V_{Rd,μικρό} = frac{V_{Rk,μικρό}}{\η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Κυρία,κουρεύω}}
= frac{45.239 \,\κείμενο{ΚΝ}}{1.25}
= 36.191 \,\κείμενο{ΚΝ}
\)
ο απαιτούμενη αντίσταση διάτμησης ανά ράβδο αγκύρωσης είναι το προκύπτον διατμητικό φορτίο διαιρούμενο με τον συνολικό αριθμό των ράβδων αγκύρωσης, που υπολογίζει να 1.77 ΚΝ.
\(
V_{Εκδ} = frac{\τ.μ.{ (V_y)^ 2 + (V_z)^ 2 }}{n_{Α.Κ.}}
\)
\(
V_{Εκδ} = frac{\τ.μ.{ (5 \,\κείμενο{ΚΝ})^ 2 + (5 \,\κείμενο{ΚΝ})^ 2 }}{4}
= 1.7678 \,\κείμενο{ΚΝ}
\)
Από 1.7678 ΚΝ < 36.191 ΚΝ, η ικανότητα διάτμησης της ράβδου αγκύρωσης είναι επαρκής.
Ελεγχος #6: Υπολογίστε τη φέρουσα ικανότητα της πλάκας βάσης
Ενα επιπλέον Έλεγχος αντίστασης ρουλεμάν πλάκας βάσης παρουσιάστηκε σε μεταγενέστερη ενημέρωση του λογισμικού. Σας παρακαλούμε ανατρέξτε σε αυτόν τον σύνδεσμο για ένα δείγμα υπολογισμού και λεπτομερή εξήγηση.
Περίληψη σχεδίου
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV Μπορεί να δημιουργήσει αυτόματα μια αναφορά υπολογισμού βήμα προς βήμα για αυτό το παράδειγμα σχεδιασμού. Παρέχει επίσης μια περίληψη των επιταγών που εκτελούνται και των προκύπτουσων αναλογιών τους, καθιστώντας τις πληροφορίες κατανοητές με μια ματιά. Παρακάτω είναι ένας πίνακας συνοπτικών δείγματος, που περιλαμβάνεται στην αναφορά.
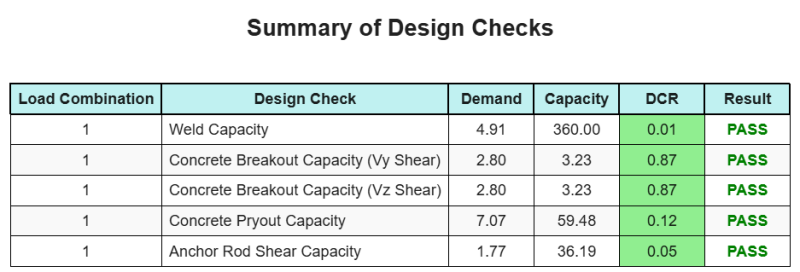
Αναφορά δείγματος SkyCIV
Δείτε το επίπεδο λεπτομέρειας και σαφήνειας που μπορείτε να περιμένετε από μια αναφορά σχεδίασης πλάκας βάσης SkyCiv. Η αναφορά περιλαμβάνει όλους τους βασικούς ελέγχους σχεδιασμού, εξισώσεις, και τα αποτελέσματα παρουσιάζονται σε σαφή και ευανάγνωστη μορφή. Είναι πλήρως συμβατό με τα πρότυπα σχεδιασμού. Κάντε κλικ παρακάτω για να προβάλετε ένα δείγμα αναφοράς που δημιουργήθηκε με χρήση του SkyCiv Base Plate Calculator.
Αγορά λογισμικού πλάκας βάσης
Αγοράστε την πλήρη έκδοση της μονάδας σχεδιασμού πλάκας βάσης από μόνη της χωρίς άλλες ενότητες SkyCIV. Αυτό σας δίνει ένα πλήρες σύνολο αποτελεσμάτων για σχεδιασμό πλάκας βάσης, συμπεριλαμβανομένων λεπτομερών αναφορών και περισσότερων λειτουργιών.