Παράδειγμα σχεδιασμού πλάκας βάσης χρησιμοποιώντας το EN 1993-1-8-2005, ΣΕ 1993-1-1-2005 και EN 1992-1-1-2004
Προβληματική δήλωση
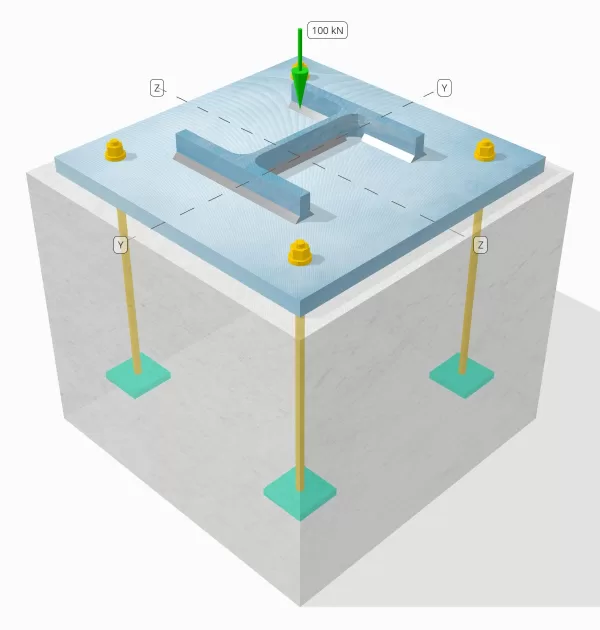
Προσδιορίστε εάν η σχεδιασμένη σύνδεση πλάκας στη στήλη σε βάση είναι επαρκής για φορτίο συμπίεσης 100 kn.
Δεδομένα
Στήλη:
Ενότητα στήλης: ΑΥΤΟΣ 200 σι
Επιφάνεια στήλης: 7808 χιλ2
Υλικό στήλης: S235
Πλάκα βάσης:
Διαστάσεις πλάκας βάσης: 400 mm x 400 χιλ
Πάχος πλάκας βάσης: 20 χιλ
Υλικό πλάκας βάσης: S235
Πηκτώ:
Πάχος ενέματα: 20 χιλ
Σκυρόδεμα:
Διαστάσεις σκυροδέματος: 450 mm x 450 χιλ
Πάχος σκυροδέματος: 380 χιλ
Σκυρόδεμα: C20/25
Συγκολλήσεις:
Το φορτίο συμπίεσης μεταφέρθηκε μόνο μέσω συγκολλήσεων? ΟΧΙ
Μοντέλο στο δωρεάν εργαλείο SkyCiv
Μοντελοποιήστε το παραπάνω σχέδιο πλάκας βάσης χρησιμοποιώντας το δωρεάν διαδικτυακό μας εργαλείο σήμερα! Δεν απαιτείται εγγραφή.
Υπολογισμοί βήμα προς βήμα
Ελεγχος #1: Υπολογίστε τη χωρητικότητα συγκόλλησης
Δεδομένου ότι το φορτίο συμπίεσης δεν μεταφέρεται μόνο μέσω συγκολλήσεων, Απαιτείται σωστή επιφάνεια εδράνου για να διασφαλιστεί ότι το φορτίο μεταφέρεται μέσω ρουλεμάν. Παραπέμπω ΣΕ 1090-2:2018 Ρήτρα 6.8 για προετοιμασία εδράνου επαφής.
Επιπροσθέτως, Χρησιμοποιήστε ελάχιστο μέγεθος συγκόλλησης καθορίζεται σε ευρωκωτικό κώδικα.
Ελεγχος #2: Υπολογίστε τη χωρητικότητα εδράνου σκυροδέματος και την ικανότητα απόδοσης πλάκας βάσης
Το πρώτο βήμα είναι να προσδιοριστεί η αντοχή σε συμπιεστική σχεδίαση της άρθρωσης, που εξαρτάται από τη γεωμετρία της υποστήριξης (σκυρόδεμα) και τη γεωμετρία της φορτωμένης περιοχής (πλάκα βάσης).
Ξεκινάμε με τον υπολογισμό του παράγοντα alpha, που αντιπροσωπεύει τη διάχυση της συμπυκνωμένης δύναμης μέσα στο ίδρυμα.
Σύμφωνα με ΣΕ 1992-1-1:2004, Ρήτρα 6.7, Ο συντελεστής άλφα είναι η αναλογία της επιφάνειας φορτωμένου στη μέγιστη περιοχή διανομής, που έχει παρόμοιο σχήμα με τη φορτωμένη περιοχή.
Θα χρησιμοποιήσουμε την εξίσωση από Μέρος 6.1 των πολυώροφων χάλυβα κτιρίων 5 με Arcelor Mittal, Μεταφορέας Peiner, και Κορδόνι Για να υπολογίσετε τον παράγοντα άλφα.
\(
\alpha = min αριστερά(
1 + \frac{αυτό είναι ένα πολύ σημαντικό στάδιο στο σχεδιασμό ενός τοίχου αντιστήριξης, καθώς η μη αντιστοίχιση των σωστών αναλογικών διαστάσεων από την αρχή σε κάθε στοιχείο μπορεί να οδηγήσει στην ανάγκη πολλών επαναλήψεων για να συμμορφωθεί ο τοίχος αντιστήριξης με τις απαιτήσεις ευστάθειας ή υπερμεγέθη σύστημα που πληροί όλες τις απαιτήσεις, αλλά χρησιμοποιεί πολύ περισσότερο υλικό από το θεωρητικό ελάχιστο{\κείμενο{σύμπλεγμα}}}{\Μέγιστη(ΜΕΓΑΛΟ_{\κείμενο{bp}}, ΣΙ_{\κείμενο{bp}})},
1 + 2 \αριστερά( \frac{εχ.}{ΜΕΓΑΛΟ_{\κείμενο{bp}}} \σωστά),
1 + 2 \αριστερά( \frac{e_b}{ΣΙ_{\κείμενο{bp}}} \σωστά),
3
\σωστά)
\)
\(
\alpha = min αριστερά(
1 + \frac{380 \, \κείμενο{χιλ}}{\Μέγιστη(400 \, \κείμενο{χιλ}, 400 \, \κείμενο{χιλ})},
1 + 2 \αριστερά( \frac{25 \, \κείμενο{χιλ}}{400 \, \κείμενο{χιλ}} \σωστά),
1 + 2 \αριστερά( \frac{25 \, \κείμενο{χιλ}}{400 \, \κείμενο{χιλ}} \σωστά),
3
\σωστά)
\)
\(
\άλφα = 1.125
\)
όπου,
\(
e_h = frac{ΜΕΓΑΛΟ_{\κείμενο{σύμπλεγμα}} – ΜΕΓΑΛΟ_{\κείμενο{bp}}}{2} = frac{450 \, \κείμενο{χιλ} – 400 \, \κείμενο{χιλ}}{2} = 25 \, \κείμενο{χιλ}
\)
\(
e_b = frac{ΣΙ_{\κείμενο{σύμπλεγμα}} – ΣΙ_{\κείμενο{bp}}}{2} = frac{450 \, \κείμενο{χιλ} – 400 \, \κείμενο{χιλ}}{2} = 25 \, \κείμενο{χιλ}
\)
Μόλις οριστεί η γεωμετρία, Στη συνέχεια, θα καθορίσουμε τη χρήση συμπιεστικής αντοχής του σκυροδέματος ΣΕ 1992-1-1:2004, Εξ. 3.15.
\(
φά_{CD} = frac{\άλφα_{Δύναμη λόγω σκυροδέματος} φά_{ck}}{\Gamma_c} = frac{1 \φορές 20 \, \κείμενο{MPa}}{1.5} = 13.333 \, \κείμενο{MPa}
\)
Επόμενο, Υποθέτουμε μια τιμή για τον συντελεστή βήτα. Δεδομένου ότι είναι παρόν, Η τιμή beta μπορεί να είναι 2/3. Θα υπολογίσουμε την αντοχή στο σχεδιασμό της άρθρωσης χρησιμοποιώντας τους συνδυασμένους τύπους από ΣΕ 1993-1-8:2005 Εξ. 6.6, και ΣΕ 1992-1-1:2004 Εξ. 6.63.
\(
φά_{jd} = beta alpha f_{CD} = 0.66667 \φορές 1.125 \φορές 13.333 \, \κείμενο{MPa} = 10 \, \κείμενο{MPa}
\)
Το δεύτερο μέρος περιλαμβάνει τον υπολογισμό της χωρητικότητας απόδοσης πλάκας βάσης.
Δεδομένου ότι έχουμε ήδη την αντοχή στο σχεδιασμό της σύνδεσης, Θα το χρησιμοποιήσουμε για να προσδιορίσουμε τη μικρότερη απόσταση προβολής της πλάκας βάσης που βιώνει το πλήρες φορτίο εδράνου. Θα αναφερθούμε στο SCI P358 Παράδειγμα στη σελίδα 243 και ΣΕ 1993-1-1:2005 Ρήτρα 6.2.5.
\(
c = t_{\κείμενο{bp}} \τ.μ.{\frac{φά_{y_{\κείμενο{bp}}}}{3 φά_{jd} \η δύναμη ολίσθησης είναι το άθροισμα της προκύπτουσας οριζόντιας δύναμης από την ενεργό πίεση του εδάφους στην ενεργή πλευρά του εδάφους και της προκύπτουσας οριζόντιας δύναμης από την παρουσία της πρόσθετης επιβάρυνσης{Μ0}}} = 20 \, \κείμενο{χιλ} \φορές sqrt{\frac{225 \, \κείμενο{MPa}}{3 \φορές 10 \, \κείμενο{MPa} \φορές 1}} = 54.772 \, \κείμενο{χιλ}
\)
Θα χρησιμοποιήσουμε αυτή τη διάσταση για να υπολογίσουμε την αποτελεσματική περιοχή της πλάκας βάσης. Το 'γ’ Η διάσταση που υπολογίσαμε μπορεί να επικαλύπτεται ή να μην επικαλύπτεται κοντά στη φλάντζα. Εάν επικαλύπτεται, Θα υποθέσουμε ότι το τμήμα είναι ένα ορθογώνιο τμήμα. Εάν δεν επικαλύπτεται, Θα πάρουμε το σχήμα της στήλης.
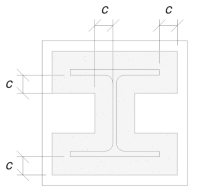
Χωρίς επικάλυψη
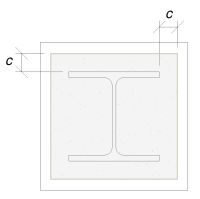
Με επικάλυψη
Διαπιστώσαμε ότι το 'γ’ Η διάσταση δεν επικαλύπτεται. Επομένως, χρησιμοποιώντας SCI P358 PG. 243, Η αποτελεσματική περιοχή είναι:
\(
A_e = 4c^2 + Π_{\κείμενο{διάσελο}}ντο + ΕΝΑ_{\κείμενο{διάσελο}} = 4 \φορές 54.772^2 \, \κείμενο{χιλ}^ 2 + 1182 \, \κείμενο{χιλ} \φορές 54.772 \, \κείμενο{χιλ} + 7808 \, \κείμενο{χιλ}💕⬛ Αγορά Indocin από 84549 \, \κείμενο{χιλ}^ 2
\)
Είναι σημαντικό να σημειωθεί ότι η αποτελεσματική περιοχή δεν πρέπει να είναι μικρότερη από την περιοχή της πλάκας βάσης.
Τελικά, θα το χρησιμοποιησουμε ΣΕ 1993-1-8:2005 Εξ. 6.6, και EN 1992-1-1:2004, Εξ. 6.63 Για τον υπολογισμό της αντίστασης του ρουλεμάν σχεδιασμού της σύνδεσης πλάκας βάσης.
\(
Ν_{Rd} = αριστερά( \ελάχ(A_e, A_0) \σωστά) φά_{jd} = αριστερά( \ελάχ(84549 \, \κείμενο{χιλ}^ 2, 160000 \, \κείμενο{χιλ}^ 2) \σωστά) \φορές 10 \, \κείμενο{MPa} = 845.49 \, \κείμενο{ΚΝ}
\)
Από 845.49 ΚΝ > 100 ΚΝ, Ο σχεδιασμός είναι επαρκής!
Περίληψη σχεδίου
Το λογισμικό σχεδιασμού πλάκας βάσης SkyCIV μπορεί να δημιουργήσει αυτόματα μια αναφορά υπολογισμού βήμα προς βήμα για αυτό το παράδειγμα σχεδιασμού. Παρέχει επίσης μια περίληψη των επιταγών που εκτελούνται και των προκύπτουσων αναλογιών τους, καθιστώντας τις πληροφορίες κατανοητές με μια ματιά. Παρακάτω είναι ένας πίνακας συνοπτικών δείγματος, που περιλαμβάνεται στην αναφορά.

Αναφορά δείγματος SkyCIV
Δείτε το επίπεδο λεπτομέρειας και σαφήνειας που μπορείτε να περιμένετε από μια αναφορά σχεδίασης πλάκας βάσης SkyCiv. Η αναφορά περιλαμβάνει όλους τους βασικούς ελέγχους σχεδιασμού, εξισώσεις, και τα αποτελέσματα παρουσιάζονται σε σαφή και ευανάγνωστη μορφή. Είναι πλήρως συμβατό με τα πρότυπα σχεδιασμού. Κάντε κλικ παρακάτω για να προβάλετε ένα δείγμα αναφοράς που δημιουργήθηκε με χρήση του SkyCiv Base Plate Calculator.
Αγορά λογισμικού πλάκας βάσης
Αγοράστε την πλήρη έκδοση της μονάδας σχεδιασμού πλάκας βάσης από μόνη της χωρίς άλλες ενότητες SkyCIV. Αυτό σας δίνει ένα πλήρες σύνολο αποτελεσμάτων για σχεδιασμό πλάκας βάσης, συμπεριλαμβανομένων λεπτομερών αναφορών και περισσότερων λειτουργιών.


