Παράδειγμα σχεδίασης πλάκας βάσης με χρήση CSA S16:19 και CSA A23.3:19
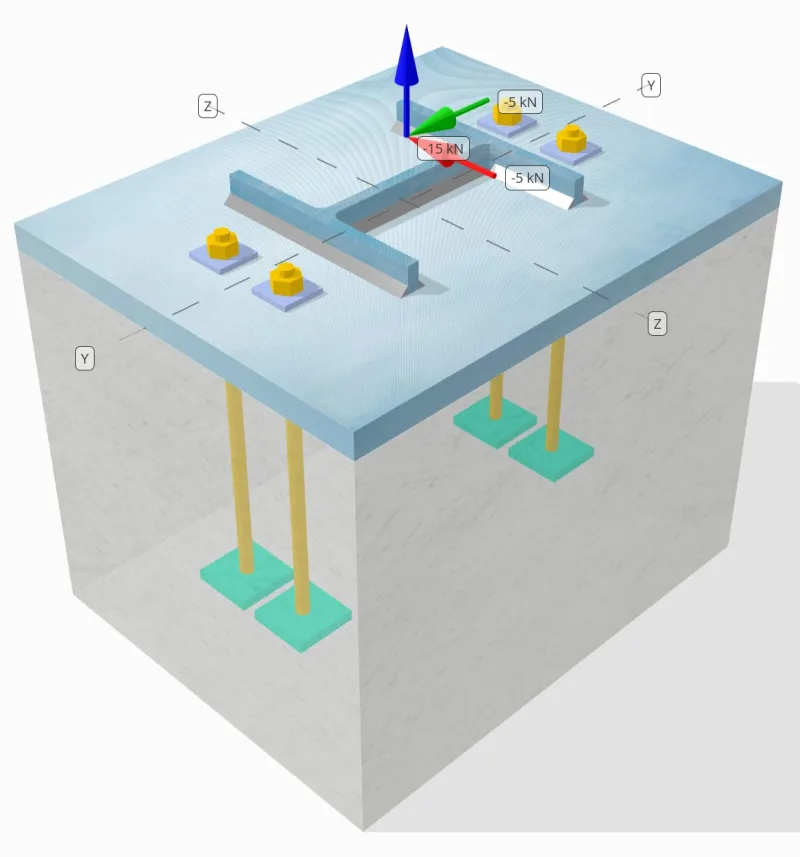
Προβληματική δήλωση
Προσδιορίστε εάν η σχεδιασμένη σύνδεση στήλης-πλάκας βάσης είναι επαρκής για 15 kN φορτίο εφελκυσμού, 5 kN Διατμητικό φορτίο, και 5 kN Vz διατμητικό φορτίο.
Δεδομένα
Στήλη:
Ενότητα στήλης: HP200x54
Επιφάνεια στήλης: 6840.0 χιλ2
Υλικό στήλης: 350Δ
Πλάκα βάσης:
Διαστάσεις πλάκας βάσης: 400 mm x 500 χιλ
Πάχος πλάκας βάσης: 25 χιλ
Υλικό πλάκας βάσης: 300Δ
Πηκτώ:
Πάχος ενέματος: 0 χιλ
Σκυρόδεμα:
Διαστάσεις σκυροδέματος: 400 mm x 500 χιλ
Πάχος σκυροδέματος: 380 χιλ
Σκυρόδεμα: 20.7 MPa
Ραγισμένα ή αδιευκρίνιστα: Ραγισμένος
Άγκυρες:
Διάμετρος άγκυρας: 12.7 χιλ
Αποτελεσματικό μήκος ενσωμάτωσης: 300 χιλ
Anchor Ending: Ορθογώνιο Πλάκα
Ενσωματωμένο πλάτος πλάκας: 60χιλ
Ενσωματωμένο πάχος πλάκας: 10 χιλ
Υλικό χάλυβα: F1554 Γρ.55
Νήματα σε επίπεδο διάτμησης: Συμπεριλαμβανομένος
Συγκολλήσεις:
Μέγεθος συγκόλλησης: 8 χιλ
Η ταξινόμηση μετάλλων πλήρωσης: E43XX-X
Δεδομένα αγκυροβόλησης (από Υπολογιστής Skyciv):
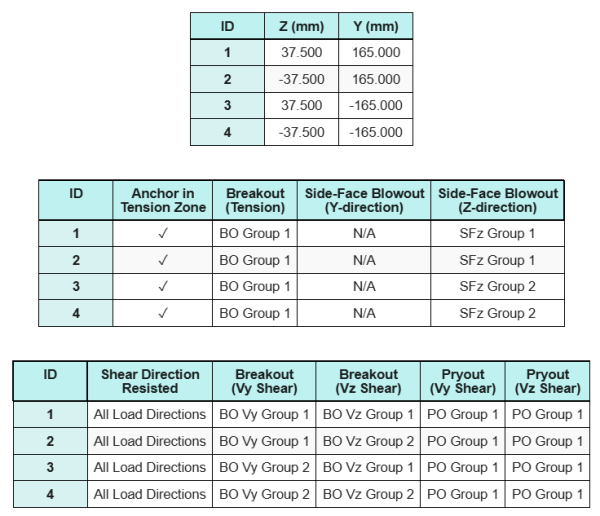
Μοντέλο στο δωρεάν εργαλείο SkyCiv
Μοντελοποιήστε το παραπάνω σχέδιο πλάκας βάσης χρησιμοποιώντας το δωρεάν διαδικτυακό μας εργαλείο σήμερα! Δεν απαιτείται εγγραφή.
Σημείωση
Ο σκοπός αυτού του παραδείγματος σχεδιασμού είναι να επιδείξει τους βαθμιαίους υπολογισμούς για ελέγχους χωρητικότητας που περιλαμβάνουν ταυτόχρονα διατμητικά και αξονικά φορτία. Ορισμένοι από τους απαιτούμενους ελέγχους έχουν ήδη συζητηθεί στα προηγούμενα παραδείγματα σχεδιασμού. Ανατρέξτε στους συνδέσμους που παρέχονται σε κάθε ενότητα.
Υπολογισμοί βήμα προς βήμα
Ελεγχος #1: Υπολογίστε τη χωρητικότητα συγκόλλησης
Για τον προσδιορισμό της ικανότητας συγκόλλησης υπό ταυτόχρονη φόρτιση, πρέπει πρώτα να υπολογίσουμε τη ζήτηση συγκόλλησης λόγω του διατμητικό φορτίο και η ζήτηση συγκόλλησης λόγω του φορτίο τάσης. Μπορείτε να αναφερθείτε σε αυτό Σύνδεσμος για τη διαδικασία λήψης των απαιτήσεων συγκόλλησης για διάτμηση, και αυτό Σύνδεσμος για τις απαιτήσεις συγκόλλησης τάσης.
Για αυτό το σχέδιο, ο weld demand at the flange λόγω του φορτίου εφελκυσμού βρέθηκε να είναι ως εξής, όπου το άγχος εκφράζεται ως δύναμη ανά μονάδα μήκους.
\( v_{φά,flg} = frac{T_{εσύ,άγκυρα}}{μεγάλο_{εφ}} = frac{3.75\,\κείμενο{ΚΝ}}{100.5\,\κείμενο{χιλ}} = 0.037313\,\text{kN / mm} \)
Επί πλέον, ο τάση συγκόλλησης σε οποιοδήποτε μέρος του τμήματος της στήλης λόγω του διατμητικού φορτίου προσδιορίζεται ως:
\( v_{κηλίδα} = frac{V_y}{ΜΕΓΑΛΟ_{συγκόλληση}} = frac{5\,\κείμενο{ΚΝ}}{1090.6\,\κείμενο{χιλ}} = 0.0045846\,\text{kN / mm} \)
\( v_{fz} = frac{V_z}{ΜΕΓΑΛΟ_{συγκόλληση}} = frac{5\,\κείμενο{ΚΝ}}{1090.6\,\κείμενο{χιλ}} = 0.0045846\,\text{kN / mm} \)
Δεδομένου ότι υπάρχει ένας συνδυασμός φορτίων εφελκυσμού και διάτμησης στο ιστός, πρέπει να λάβουμε το αποτέλεσμα. Εκφράζοντας αυτό ως δύναμη ανά μονάδα μήκους, έχουμε:
\(r_f = sqrt{(r_{φά,\κείμενο{flg}})^ 2 + (v_{κηλίδα})^ 2 + (v_{fz})^ 2}\)
\( r_f = sqrt{(0.037313\,\κείμενο{kN / mm})^ 2 + (0.0045846\,\κείμενο{kN / mm})^ 2 + (0.0045846\,\κείμενο{kN / mm})^ 2} \)
\(r_f = 0.037873\ \κείμενο{kN / mm}\)
Για το ιστός, υπάρχουν μόνο διατμητικές τάσεις. Ετσι, το αποτέλεσμα είναι:
\( r_f = sqrt{((v_{κηλίδα})^ 2) + ((v_{fz})^ 2)} \)
\( r_f = sqrt{((0.0045846\,\κείμενο{kN / mm})^ 2) + ((0.0045846\,\κείμενο{kN / mm})^ 2)} = 0.0064836\,\text{kN / mm} \)
Επόμενο, υπολογίζουμε το factored weld capacity χρησιμοποιώντας CSA S16:19 Ρήτρα 13.13.2.2. We conservatively assume kds = 1.0, by always setting angle of load to 0 εσείς, neglecting any additional capacity added by the actual load angle.
\( v_{ρ,ιστός} = 0.67\phi t_wX_u = 0.67 \φορές 0.67 \times 5.657\,\text{χιλ} \times 430\,\text{MPa} = 1,092,κείμενο{kN / mm} \)
\( v_{ρ,flg} = 0.67\phi t_wX_u = 0.67 \φορές 0.67 \times 5.657\,\text{χιλ} \times 430\,\text{MPa} = 1,092,κείμενο{kN / mm} \)
Για αυτή τη συγκολλημένη σύνδεση, την αντοχή του ηλεκτροδίου δεν υπερταιριάζει τις αντοχές του βασικού μετάλλου. Επομένως, ο έλεγχος βασικών μετάλλων δεν διέπει και δεν χρειάζεται να γίνει.
Από 0.0064836 kN / mm < 1.092 kN / mm και 0.037873 kN / mm < 1.092 kN / mm, Η χωρητικότητα συγκόλλησης είναι επαρκής.
Ελεγχος #2: Υπολογίστε τη χωρητικότητα κάμψης πλάκας βάσης λόγω φορτίου τάσης
Ένα παράδειγμα σχεδίασης για την ικανότητα κάμψης της πλάκας βάσης έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για τάση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #3: Υπολογίστε την ικανότητα εφελκυσμού της ράβδου άγκυρας
Ένα παράδειγμα σχεδίασης για την ικανότητα εφελκυσμού της ράβδου αγκύρωσης έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για την τάση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #4: Υπολογίστε τη χωρητικότητα ξεμπλοκάρισμα από σκυρόδεμα σε ένταση
Ένα παράδειγμα σχεδίασης για την ικανότητα του σκυροδέματος σε διάσπαση τάσης έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για τάση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #5: Υπολογίστε την χωρητικότητα αγκύρωσης
Ένα παράδειγμα σχεδίασης για την ικανότητα έλξης αγκύρωσης έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για τάση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #6: Υπολογίστε την ικανότητα κάμψης της πλάκας
Ένα παράδειγμα σχεδίασης για τον συμπληρωματικό έλεγχο της ικανότητας κάμψης της ενσωματωμένης πλάκας έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για τάση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #7: Υπολογίστε την χωρητικότητα εκτόξευσης πλευρικού προσώπου σε κατεύθυνση y
Side-face blowout failure along the Y-direction is not applicable because the anchors are not located close enough to the left and right edges of the concrete support.
Ελεγχος #8: Υπολογίστε την χωρητικότητα εκτόξευσης πλευρικού προσώπου στην κατεύθυνση z

Για να υπολογίσετε το Έκρηξη στο πλάι του προσώπου (SFBO) χωρητικότητα, προσδιορίζουμε πρώτα το σύνολο δύναμη τάσης στις άγκυρες που βρίσκονται πιο κοντά στην άκρη. Για αυτόν τον έλεγχο, θα αξιολογήσουμε την χωρητικότητα της άκρης κατά μήκος του Z-κατεύθυνση.
Since the failure cone projections of the SFBO along the Z-direction overlap, οι άγκυρες αντιμετωπίζονται ως ένα ομάδα άγκυρας.
Η συνολική ζήτηση τάσης της ομάδας αγκύρωσης υπολογίζεται ως:
\( Ν_{φά} = αριστερά(\frac{N_z}{n_{ένα,τ}}\σωστά)n_{με,G1} = αριστερά(\frac{15\,\κείμενο{ΚΝ}}{4}\σωστά) \φορές 2 = 7.5\,\text{ΚΝ} \)
Επόμενο, καθορίζουμε το αποστάσεις ακμών:
\( ντο_{και,ελάχ} = min(ντο_{\κείμενο{μπλουζα},G1}, ντο_{\κείμενο{κάτω μέρος},G1}) = min(85\,\κείμενο{χιλ}, 415\,\κείμενο{χιλ}) = 85\,\text{χιλ} \)
\( ντο_{με,ελάχ} = min(ντο_{\κείμενο{αριστερά},G1}, ντο_{\κείμενο{σωστά},G1}) = min(162.5\,\κείμενο{χιλ}, 162.5\,\κείμενο{χιλ}) = 162.5\,\text{χιλ} \)
Χρησιμοποιώντας αυτές τις αποστάσεις ακμών, υπολογίζουμε το χωρητικότητα ομάδας αγκύρωσης συμφωνώς προς CSA A23.3:19 Ρήτρα Δ.6.4.
\( Ν_{sbgr} = αριστερά(\frac{1 + \frac{ντο_{με,ελάχ}}{ντο_{και,ελάχ}}}{4} + \frac{μικρό_{άθροισμα,με,G1}}{6ντο_{και,ελάχ}}\σωστά)13.3\αριστερά(\frac{ντο_{και,ελάχ}}{χιλ}\σωστά)\τ.μ.{\frac{ΕΝΑ_{brg}}{mm^2}}\philambda_asqrt{\frac{f'_c}{MPa}}Ρ(Ν) \)
\( Ν_{sbgr} = αριστερά(\frac{1 + \frac{162.5\,\κείμενο{χιλ}}{85\,\κείμενο{χιλ}}}{4} + \frac{75\,\κείμενο{χιλ}}{6 \times 85\,\text{χιλ}}\σωστά) \φορές 13.3 \φορές αριστερά(\frac{85\,\κείμενο{χιλ}}{1\,\κείμενο{χιλ}}\σωστά) \φορές sqrt{\frac{3473.3\,\κείμενο{χιλ}^ 2}{1\,\κείμενο{χιλ}^ 2}} \φορές 0.65 \φορές 1 \φορές sqrt{\frac{20.68\,\κείμενο{MPa}}{1\,\κείμενο{MPa}}} \φορές 1 \φορές 0,001,κείμενο{ΚΝ} \)
\( Ν_{sbgr} = 172.32\,\text{ΚΝ} \)
Στην αρχική εξίσωση, εφαρμόζεται ένας συντελεστής μείωσης όταν η απόσταση αγκύρωσης είναι μικρότερη από 6ca1, υποθέτοντας ότι οι αγκυρώσεις με κεφαλή έχουν επαρκή απόσταση ακμών. Ωστόσο, σε αυτό το παράδειγμα σχεδίασης, Από περίπου < 3ca1, η αριθμομηχανή SkyCiv εφαρμόζει έναν πρόσθετο συντελεστή μείωσης για να υπολογίσει τη μειωμένη χωρητικότητα των άκρων.
Από 7.5 ΚΝ < 172.32 ΚΝ, η χωρητικότητα SFBO κατά μήκος της κατεύθυνσης Z είναι επαρκής.
Ελεγχος #9: Υπολογίστε την ικανότητα διάσπασης (Με διάτμηση)
Ένα παράδειγμα σχεδίασης για την ικανότητα διάσπασης σκυροδέματος σε διάτμηση Vy έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για διάτμηση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #10: Υπολογίστε την ικανότητα διάσπασης (Vz διάτμηση)
Ένα παράδειγμα σχεδίασης για την ικανότητα διάσπασης σκυροδέματος σε διάτμηση Vy έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για διάτμηση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #11: Υπολογίστε την ικανότητα εκτόξευσης (Με διάτμηση)
Ένα παράδειγμα σχεδίασης για την ικανότητα του σκυροδέματος έναντι αστοχίας εκροής λόγω διάτμησης Vy έχει ήδη συζητηθεί στο Παράδειγμα Σχεδιασμού Πλάκας Βάσης για Διάτμηση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #12: Υπολογίστε την ικανότητα εκτόξευσης (Vz διάτμηση)
Ένα παράδειγμα σχεδίασης για την ικανότητα του σκυροδέματος έναντι αστοχίας εκροής λόγω διάτμησης Vy έχει ήδη συζητηθεί στο Παράδειγμα Σχεδιασμού Πλάκας Βάσης για Διάτμηση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #13: Υπολογίστε την ικανότητα διάτμησης της ράβδου αγκύρωσης
Ένα παράδειγμα σχεδίασης για την ικανότητα διάτμησης της ράβδου αγκύρωσης έχει ήδη συζητηθεί στο Παράδειγμα σχεδίασης πλάκας βάσης για διάτμηση. Ανατρέξτε σε αυτόν τον σύνδεσμο για τον βήμα προς βήμα υπολογισμό.
Ελεγχος #14: Calculate anchor rod shear and tension capacity (CSA S16)
Για τον προσδιορισμό της χωρητικότητας της ράβδου αγκύρωσης υπό συνδυασμένα διατμητικά και αξονικά φορτία, χρησιμοποιούμε CSA S16:19 Ρήτρα 13.12.1.4.
The total tensile force experienced by the anchors, including additional bending from eccentric shear load is shown below.
\( T_{φά,σύνολο} = T_f + Ν_{φά} = 18.038\,\text{ΚΝ} + 3.75\,\κείμενο{ΚΝ} = 21.788\,\text{ΚΝ} \)
Using the demand and capacity values for both shear and tension checks performed, we now calculate the interaction equation.
\( I = \left(\αριστερά(\frac{V_{φά}}{V_{ντο,ω}}\σωστά)^2δεξιά) + \αριστερά(\αριστερά(\frac{T_{φά,σύνολο}}{T_c}\σωστά)^2δεξιά) \)
\( I = \left(\αριστερά(\frac{3.5355\,\κείμενο{ΚΝ}}{14.255\,\κείμενο{ΚΝ}}\σωστά)^2δεξιά) + \αριστερά(\αριστερά(\frac{21.788\,\κείμενο{ΚΝ}}{28.85\,\κείμενο{ΚΝ}}\σωστά)^2δεξιά) = 0.63189 \)
Από 0.63 < 1.0, the anchor rod interaction capacity per CSA S16 is επαρκής.
Ελεγχος #15: Υπολογίστε τους ελέγχους αλληλεπίδρασης (CSA A23.3)
Κατά τον έλεγχο της χωρητικότητας της ράβδου αγκύρωσης υπό συνδυασμένα φορτία διάτμησης και εφελκυσμού χρησιμοποιώντας CSA A23.3, εφαρμόζεται μια διαφορετική προσέγγιση. Για πληρότητα, εκτελούμε επίσης το CSA A23.3 interaction checks σε αυτόν τον υπολογισμό, που περιλαμβάνουν άλλα συγκεκριμένους ελέγχους αλληλεπίδρασης επισης.
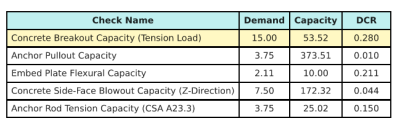
Εδώ είναι το αποτέλεσμα ratios for all CSA A23.3 tension checks:
Και ιδού τα αποτελέσματα ratios for all CSA A23.3 shear checks:
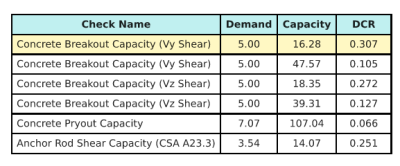
We take the design check with the largest ratio and compare it to the maximum interaction ratio using CSA A23.3:19 Equation D.46.
\( ΕΓΩ_{int} = frac{Ν_{φά}}{Ν_{έξω}} + \frac{V_{φά}}{V_{έξω}} = frac{15}{53.52} + \frac{5}{16.278} = 0.58743 \)
Από 0.587 < 1.2, ο έλεγχος αλληλεπίδρασης είναι επαρκής.
Περίληψη σχεδίου
ο Λογισμικό σχεδιασμού πλάκας βάσης SkyCIV Μπορεί να δημιουργήσει αυτόματα μια αναφορά υπολογισμού βήμα προς βήμα για αυτό το παράδειγμα σχεδιασμού. Παρέχει επίσης μια περίληψη των επιταγών που εκτελούνται και των προκύπτουσων αναλογιών τους, καθιστώντας τις πληροφορίες κατανοητές με μια ματιά. Παρακάτω είναι ένας πίνακας συνοπτικών δείγματος, που περιλαμβάνεται στην αναφορά.
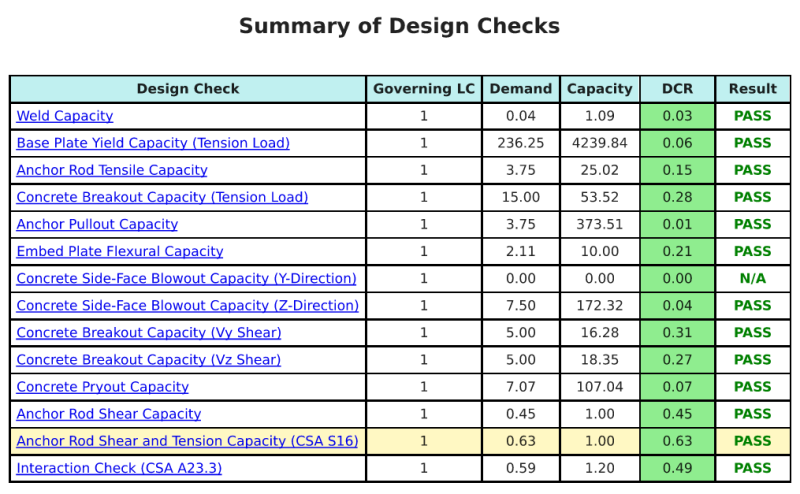
Αναφορά δείγματος SkyCIV
Δείτε το επίπεδο λεπτομέρειας και σαφήνειας που μπορείτε να περιμένετε από μια αναφορά σχεδίασης πλάκας βάσης SkyCiv. Η αναφορά περιλαμβάνει όλους τους βασικούς ελέγχους σχεδιασμού, εξισώσεις, και τα αποτελέσματα παρουσιάζονται σε σαφή και ευανάγνωστη μορφή. Είναι πλήρως συμβατό με τα πρότυπα σχεδιασμού. Κάντε κλικ παρακάτω για να προβάλετε ένα δείγμα αναφοράς που δημιουργήθηκε με χρήση του SkyCiv Base Plate Calculator.
Αγορά λογισμικού πλάκας βάσης
Αγοράστε την πλήρη έκδοση της μονάδας σχεδιασμού πλάκας βάσης από μόνη της χωρίς άλλες ενότητες SkyCIV. Αυτό σας δίνει ένα πλήρες σύνολο αποτελεσμάτων για σχεδιασμό πλάκας βάσης, συμπεριλαμβανομένων λεπτομερών αναφορών και περισσότερων λειτουργιών.


