lezione: Come risolvere una struttura a traliccio utilizzando il metodo delle sezioni

In questo tutorial, esploreremo e impareremo i vantaggi dell'utilizzo del Metodo delle sezioni per risolvere la tua struttura a traliccio. Cosa sono i tralicci?? Se non sei sicuro di questo, visita il nostro Cos'è un traliccio? articolo. Il metodo delle sezioni viene utilizzato per risolvere rapidamente strutture reticolari più grandi, modo semplice. Si tratta di prendere un "taglio"’ attraverso un numero di membri per valutare le loro forze assiali e utilizzare questo come base per risolvere il resto della struttura reticolare.

La cosa grandiosa è, Aggiungi Supporti illimitati con il pieno controllo sui loro codici di ritenuta lo fa automaticamente per te. Modella i tuoi tralicci e il software mostrerà l'elaborazione interattiva passo dopo passo del metodo delle sezioni!

Guarda il video tutorial

Esempio di domanda

Per il nostro esempio lavorato, esamineremo la seguente domanda:

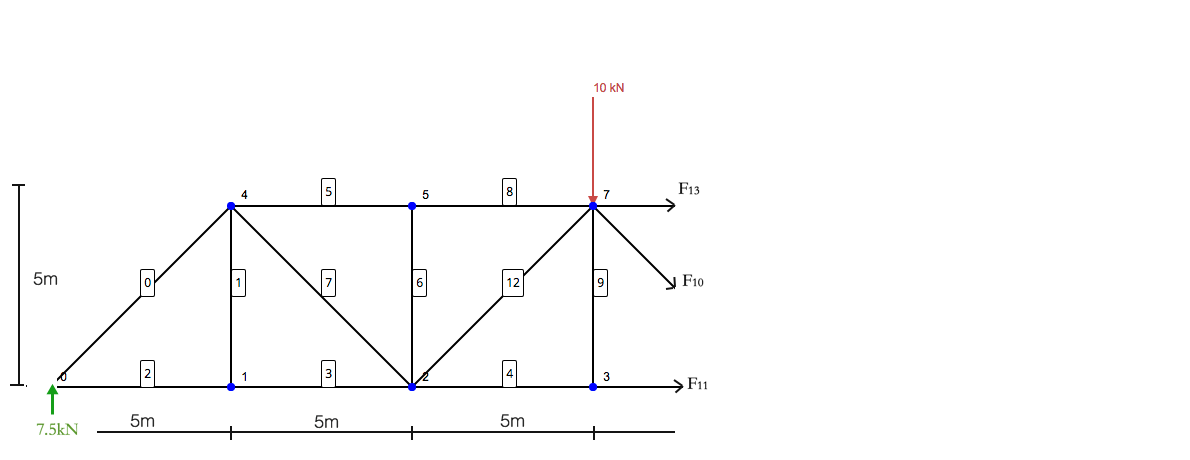
Domanda: Usando il metodo delle sezioni, determinare le forze nei membri 10, 11, e 13 della seguente struttura a traliccio:

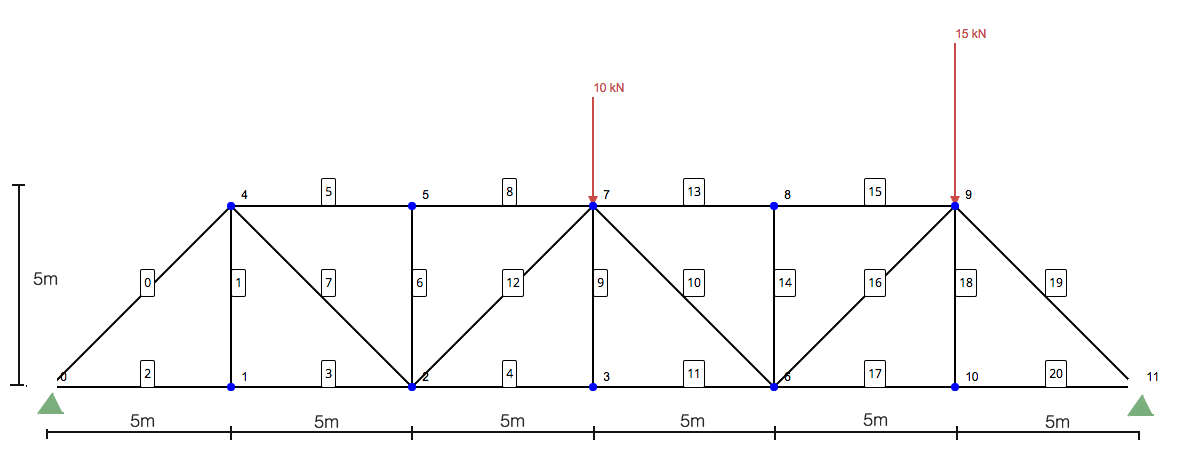
Step 1: Calcola le reazioni ai supporti

Come la maggior parte delle analisi strutturali statiche, dobbiamo prima iniziare individuando e risolvendo il reazioni a supporti. Questo ci darà le condizioni al contorno di cui abbiamo bisogno per progredire nella risoluzione della struttura reticolare. Semplificare la struttura per includere solo i carichi e i supporti:

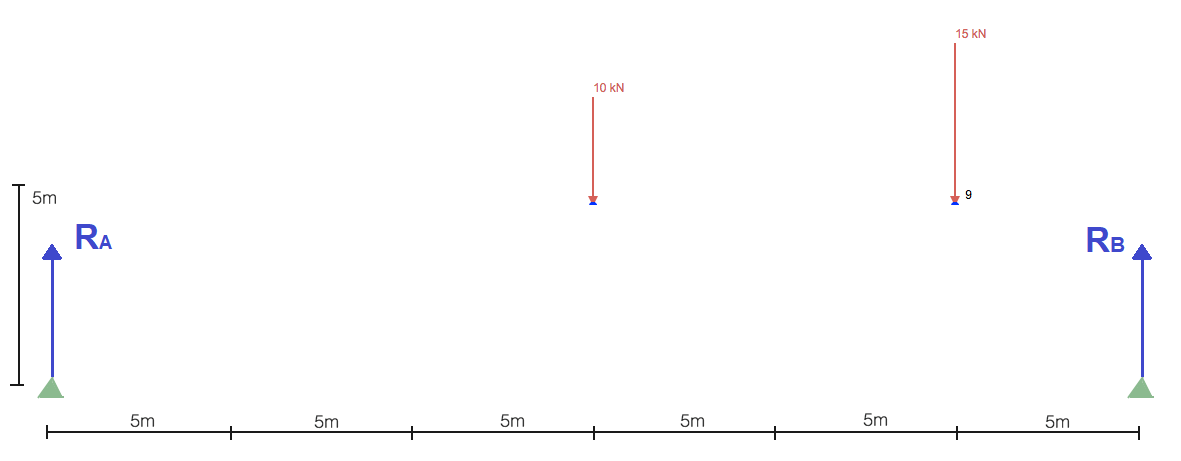
Senza spendere troppo tempo a calcolare le reazioni, generalmente inizi prendendo la somma dei momenti su un punto. Prendere la somma dei momenti sul supporto di sinistra ci fa:

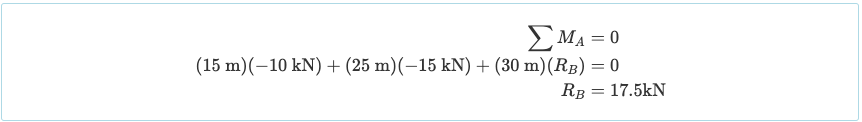
Quindi la reazione al giusto supporto (R_B) è 17.5 kN verso l'alto. Adesso, prendendo la somma delle forze in y si ottiene la reazione R_A come 7,5 kN verso l'alto:

Step 2: Fai un taglio lungo i membri di interesse

Qui arriva la parte più importante della risoluzione di un truss usando il metodo delle sezioni. Si tratta di fare una fetta attraverso i membri che si desidera risolvere. Questo metodo di analisi strutturale è estremamente utile quando si cerca di risolvere alcuni degli elementi senza dover risolvere l'intera struttura utilizzando il metodo dei giunti. Quindi, nel nostro esempio qui sarebbe la nostra fetta:

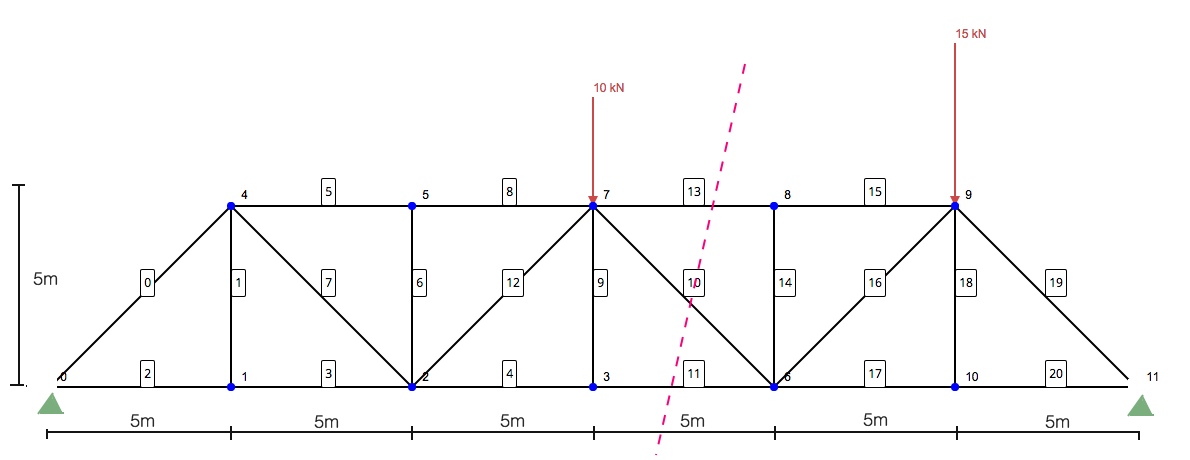
Concentrandosi solo sul lato sinistro, ti rimane la seguente struttura:

Ora pensa a questa struttura come a una struttura a sé stante. Le leggi della statica si applicano ancora – quindi la somma dei momenti e delle forze deve essere uguale a zero. I membri con le frecce (F₁₃, F₁₀, F₁₁) sono ciò che stabilizza la reazione e le forze applicate alla struttura. Nota che la somma dei momenti è presa intorno al nodo 7 – come escluderebbe le forze dei membri 13 e 10 – lasciando F₁₁ essere isolato.

Usando il diagramma di corpo libero sopra, possiamo ottenere le seguenti formule:

Somma delle forze nella direzione y:

[matematica]
\inizio{allineare}
+\uparrow testo{ } \somma{F_y} &= 0\\
7.5\testo{ kN} – 10 \testo{ kN} – F_{10}senza(45^{\circ}) &= 0\\
F_{10} &= -3.536 \testo{ kN}
\fine{allineare}
[matematica]

Somma dei momenti sul nodo 7:

[matematica]
\inizio{allineare}
+\circlearrowleft text{ } \somma{M_7} &= 0\\
-(15 \testo{ m})(7.5 \testo{ kN}) + (5 \testo{ m})F_{11} &= 0\\
F_{11} &= 22.5 \testo{ kN}
\fine{allineare}
[matematica]

Somma delle forze nella direzione x:

[matematica]
\inizio{allineare}
+\freccia destra testo{ } \somma{F_x} &= 0\\
F_{13} + F_{11} + F_{10}cos(45^{\circ}) &= 0\\
F_{13} &= -FA_{11} – F_{10}cos(45^{\circ}) \\
F_{13} &= – (22.5 \testo{ kN}) – (-3.536 \testo{ kN})cos(45^{\circ}) \\
F_{13} &= -22.5 \testo{ kN} + (3.536 \testo{ kN})cos(45^{\circ}) \\
F_{13} &= -20 \testo{ kN}
\fine{allineare}
[matematica]

Soluzione finale

Possiamo usare questi risultati per risolvere i membri rimanenti nella struttura reticolare. Ci auguriamo che questo esempio di calcolo del traliccio sia stato utile e sentiti libero di commentare con le tue domande di seguito. Come referenza, i risultati per l'intera struttura Truss sono disponibili di seguito (usando il nostro Calcolatore della capriata) che è ottimo per controllare le tue risposte!

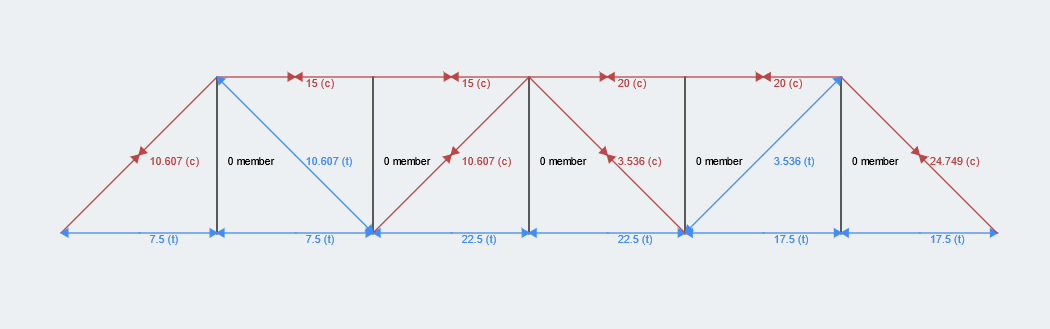
Riepilogo dei passaggi

• Inizia sempre calcolando le reazioni ai supporti
• Fai una fetta attraverso i membri che desideri risolvere
• Tratta la mezza struttura come la propria travatura statica
• Risolvi la capriata facendo la somma delle forze = 0
• Prendi il momento su un nodo di più di un membro sconosciuto

SkyCiv Truss Software

Ci auguriamo che tu abbia trovato questo tutorial utile per i tuoi progetti. Visita il nostro tutorial sul traliccio per ulteriori informazioni utili sul traliccio e non dimenticare di controllare il nostro guida alla risoluzione del traliccio con il metodo dei giunti.

Aggiungi Supporti illimitati con il pieno controllo sui loro codici di ritenuta può calcolare automaticamente il metodo delle sezioni per te. Oppure prova il nostro Calcolatore di traliccio gratuito che ti darà la risposta finale (nessun calcolo manuale).

Per esplorare più funzionalità del software SkyCiv, iscriviti oggi per iniziare!

Comincia gratuitamente