Descrizione generale
SkyCiv ha un modulo robusto e avanzato per la progettazione di lastre in cemento armato. Per accedere a questa funzione, devi prima aver costruito un modello su SkyCiv S3D e poi chiamare il modulo per il calcolo automatico con diversi codici di costruzione come ACI-318, Standard europei e australiani, e così via. Lo scopo principale del modulo per la progettazione della piastra è fornire la quantità di armature di rinforzo in acciaio lungo la piastra.
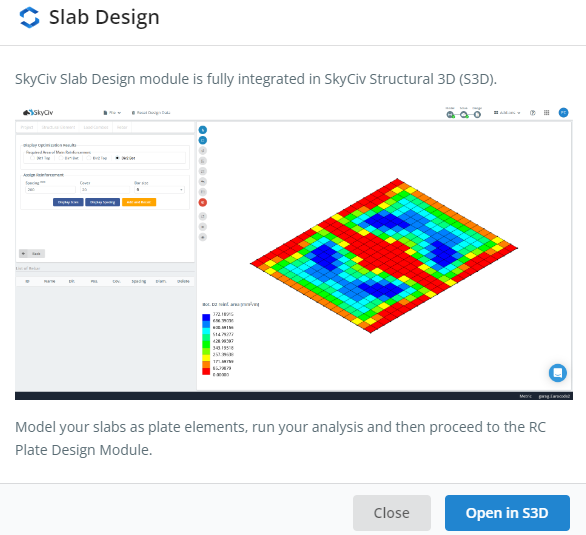
figura 1. Modulo di progettazione lastra SkyCiv
Se sei nuovo in SkyCiv, Iscriviti e testa tu stesso il software!
La documentazione SkyCiv fornisce contenuti eccellenti, inclusi esempi e casi di analisi, sia per imparare se sei nuovo ai moduli sia per confrontare i risultati del modulo di progettazione della lastra con i calcoli manuali. Sentiti libero di controllare i nostri esempi di design in base a ACI-318, Eurocodice, e AS3600.
Ti suggeriamo di leggere questo articolo prima di analizzare in profondità i sistemi di solai complessi. Qui, imparerai come i momenti flettenti differiscono a seconda delle dimensioni del piano della soletta. Ci sono due casi di studio, lastre unidirezionali e bidirezionali. Quindi, iniziamo a leggere!
Comportamento solaio unidirezionale contro bidirezionale
Consideriamo l'esempio della lastra nell'immagine seguente, dove c'è un supporto su ciascun bordo della lastra, e stabiliamo che questo si comporterà come un piatto a due vie, questo è, avente un momento flettente nelle due principali direzioni in pianta.
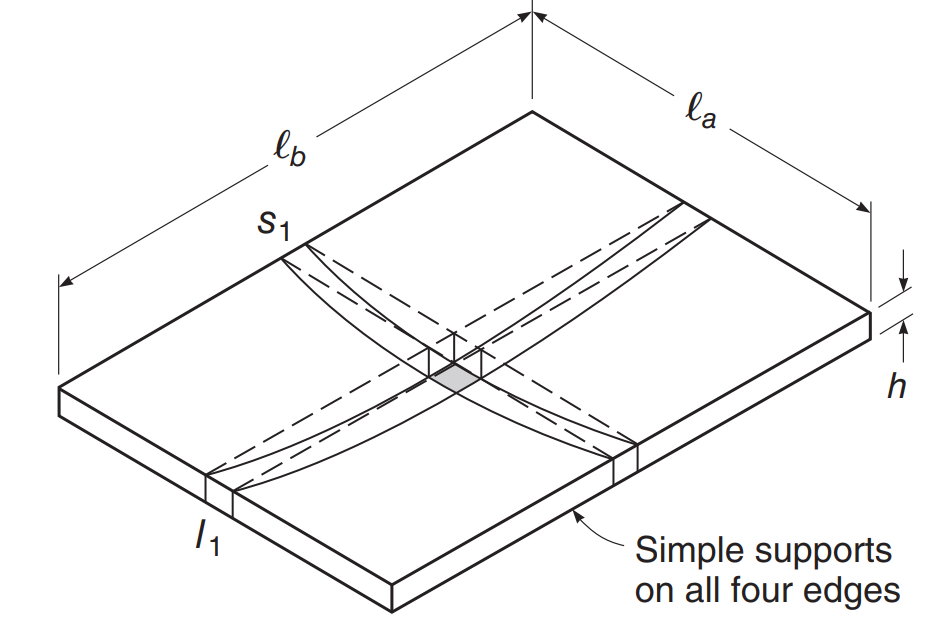
figura 2. Semplice esempio di soletta a due vie su flessione. (Davide Darwin, Charles W.Dolan, Arthur H. Nilson, “Progettazione di strutture in calcestruzzo,” Quindicesima edizione, McGraw-Hill Education)
Possiamo definire lo spostamento verticale come (\(la < libbre \)):
\(\Delta_a = frac{{5}{w_a}{l_a^4}}{384{E}{I}}\)
\(\Delta_b = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
Poiché la lastra è un sistema continuo, entrambe le deviazioni verticali avranno lo stesso valore. Possiamo confrontare le equazioni per esprimere una relazione tra il carico portato da ciascuna direzione in funzione delle dimensioni in pianta.
\(\Delta_a = Delta_b to frac{{5}{w_a}{l_a^4}}{384{E}{I}} = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
\(\frac{w_a}{w_b} = {(\frac{libbre}{la}})^4 \)
Tutti i riferimenti in cemento armato per la progettazione dei solai si dividono in unidirezionali e bidirezionali se il quoziente di \(\frac{libbre}{la}\) è maggiore o minore di un valore di 2, rispettivamente.
Usando le equazioni di cui sopra, Quando \(\frac{libbre}{la}=2), il carico trasportato dalla direzione breve è uguale a \(w_a = {16}{w_b}\) e quando il valore è \(\frac{libbre}{la}=1), il carico è distribuito equamente in entrambe le direzioni \(w_a ={w_b}\).
Momenti lastre unidirezionali
Quindi, possiamo vederlo quando il quoziente delle dimensioni è maggiore di 2, in pratica, tutti i carichi ei momenti flettenti saranno concentrati solo nella direzione breve. Questo caso è il comportamento del solaio unidirezionale, e il massimo momento flettente può essere ottenuto come trave semplicemente appoggiata di larghezza unitaria.
\(M_{max,1,D}= Frac{{w_a}{1 m}{l_a^2}}{8}\)
Momenti di lastre bidirezionali
La soluzione del caso della soletta a due vie è un problema complesso e impegnativo di meccanica strutturale. Puoi vedere nella figura sotto l'analisi generale costituita da una piastra con intere forze e momenti in ciascuna direzione.
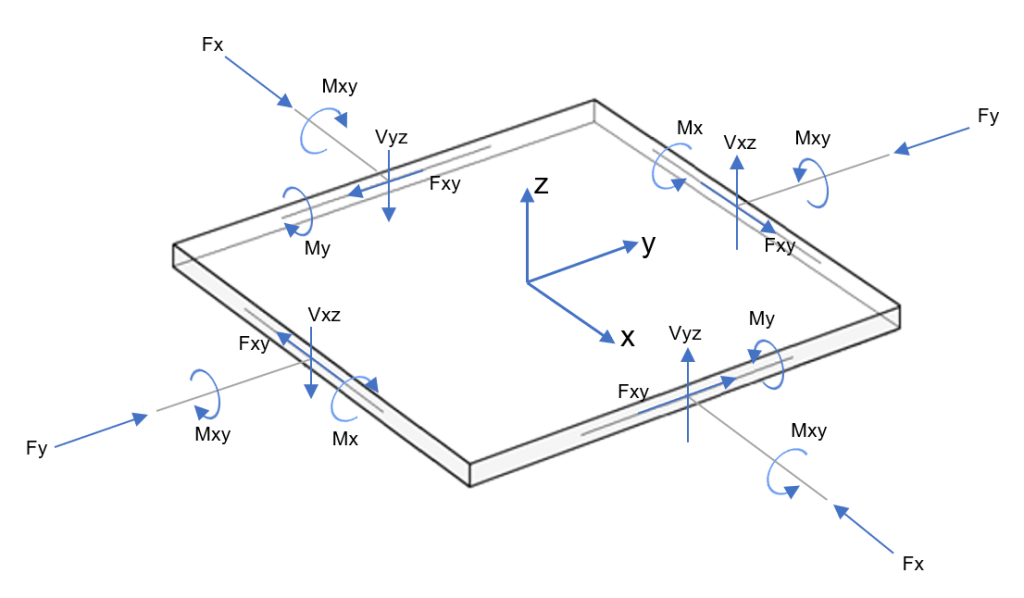
figura 3. Azioni su elemento piastra (momenti flettenti e torsionali; forze normali e di taglio)
Questa difficoltà deriva dal fatto che il vero problema da risolvere è un'equazione alle derivate parziali del quarto ordine che comporta la flessione in due direzioni. La forma di questa equazione è:
\(\frac{\parziale^4{w}}{{\parziale}{x^4}} + {2}\frac{{\parziale^4}{w}}{{{\parziale}{x^2}}{{\parziale}{e^2}}}+\frac{\parziale^4{w}}{{\parziale}{x^4}}-\frac{f_z}{D} = 0\)
Dove la rigidità del piatto (utilizzando le proprietà meccaniche e geometriche elastiche) è \(D=fraz{{E}{t^3}}{{12}{(1-\no^2)}}\).
La soluzione analitica di questa equazione è disponibile solo per condizioni di supporto semplici. L'unico modo per ottenere una possibile soluzione per casi reali e pratici è attraverso metodi numerici come il metodo degli elementi finiti.
SkyCiv utilizza questo approccio per risolvere l'analisi delle lastre. Sui seguenti link, avrai accesso a tutorial per conoscere le caratteristiche della piattaforma SkyCiv: Progettazione di lastre in S3D e Come modellare i piatti? .
Se sei nuovo in SkyCiv, Iscriviti e testa tu stesso il software!


